基于B样条的可加Logistic模型估计 Estimation of Additive Logistic Model Based on B-Spline

doi:10.12677/PM.2024.142060

Pure Mathematics
Vol. 14 No. 02 ( 2024 ), Article ID: 81726 , 12 pages
10.12677/PM.2024.142060

基于B样条的可加Logistic模型估计

昝思吕

●How to Cite this Article

贵州大学数学与统计学院，贵州贵阳

收稿日期：2024年1月8日；录用日期：2024年1月23日；发布日期：2024年2月29日

摘要

非参数模型因不需要事先假定函数形式，所以相较于参数模型更有灵活性和适应性，但存在维数灾难问题。可加模型的提出能有效克服这一问题，同时又能保留非参数的优点。本文针对可加Logistic模型，采用B样条近似，结合极大似然思想得到函数的估计，并证明了其最优收敛速度。同时通过数值模拟和实证分析，比较了可加Logistic模型和Logistic模型的表现，结果说明可加Logistic模型的表现更优。

关键词

Logistic模型，可加Logistic模型，B样条

Estimation of Additive Logistic Model Based on B-Spline

Silv Zan

School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou

Received: Jan. 8^th, 2024; accepted: Jan. 23^rd, 2024; published: Feb. 29^th, 2024

ABSTRACT

Nonparametric model is more flexible and adaptive than parametric model because it does not need to assume the function form in advance, but it has the problem of dimensional disaster. The additive model can effectively overcome this problem, while retaining the advantages of nonparameters. The paper uses B-spline for approximating additive Logistic model, and adopts the maximum likelihood idea to estimate the function, and proves the optimal convergence rate. Meanwhile, through numerical simulation and empirical analysis, the performance of the additive Logistic model and the logistic model was compared, and the results showed that the additive logistic model performed better.

Keywords:Logistic Model, Additive Logistic Model, B Spline

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

传统的参数模型需事先假设模型形式再求解其中的参数，具有易解释性，但其精度依赖于模型是否假定正确。实际情况中，某些数据无法知道其具体服从的模型形式，当假定的模型形式与实际情况差异很大时，基于假定模型得到的结论可能是完全错误的。为解决这一问题，提出了非参数模型：

$Y = m (X) + ε$

其中，Y为响应变量，X为p维协变量， $m (\cdot)$ 为未知函数， $ε$ 为随机误差，满足 $E (ε | X) = 0$ 。

要使得 $m (X)$ 在X处得到较精确的估计，就必须要在X的领域内包含足够多的数据。当X的维数增大时，估计所需要的数据个数就成指数倍增加。例如，一个局部领域沿着每一个坐标轴包含a个数据，在p维领域就需要 $a^{p}$ 个数据点。因为高维空间会使得数据更稀疏，为获取足够多的数据进行估计，可以增大带宽或者增加样本数，但增大带宽会导致估计的偏差增大，增加样本数在许多情况下是不实际的。即，当协变量维数增加时，多元非参数回归估计的精度下降很快，这种现象叫“维数灾难”。可加模型是克服这一问题的有效方法：

$Y = \sum_{j = 1}^{p} f_{j} (X_{j}) + ε$

其中，Y为响应变量， $X_{j}$ 为协变量， $f_{j} (\cdot)$ 为关于 $X_{j}$ 的光滑函数，为保证模型的可识别性，满足 $E (f_{j} (\cdot)) = 0$ ， $ε$ 为随机误差。因为可加模型将非参数回归中的多维光滑问题削减为一维光滑问题，所以避免了多维数据中的“维数灾难”问题。

实际问题中，遇到响应变量的取值为离散值时，常使用广义线性模型：

$g (μ) = X^{T} β + α$ (1)

其中， $μ = E (Y)$ ，响应变量Y服从指数分布族中某一分布， $g (\cdot)$ 为链接函数，X为p维协变量， $β$ 为p维待估参数。

使用模型(1)仍事先假设了协变量对响应变量的影响是线性的，这不能很好地反应出变量间的其他非线性关系，所以考虑将非参数可加的思想引入到其中，得到广义可加模型，其具体形式如下：

$g (μ) = \sum_{j = 1}^{p} f_{j} (X_{j}) + α$

其中， $μ = E (Y)$ ，响应变量Y服从指数分布族中某一分布， $g (\cdot)$ 为链接函数， $X_{j}$ 为协变量， $f_{j} (\cdot)$ 为未知函数，为保证模型的可识别性，满足 $E (f_{j} (\cdot)) = 0$ ， $α$ 为常数项。

广义可加模型由Hastie和Tibshirani (1990) [1] 提出，其作为广义线性模型的一种推广，结合了广义线性模型和可加模型的优点：即可以解决响应变量离散以及非正态时的建模问题；不需事先假定协变量与响应变量之间具体的关系，降低了广义线性模型中由线性假定造成的偏差。因广义可加模型的灵活性，现许多学者对其进行研究与应用。Horowitz和Mammen (2004) [2] 提出一种两阶段方法估计广义可加模型，并证明了当可加分量函数连续两次可微时，该方法所得到的估计量具有oracle性质，该估计量是渐近正态分布的。Alimadad和Salibian-Barrera (2011) [3] 基于反拟合算法讨论了广义可加模型的outlier-稳健拟合问题，证明了所得到的估计的平均函数的统计性质。Wood (2008) [4] 提出了一种计算效率高的方法用于广义可加模型的光滑度选择。Liu等(2013) [5] 提出样条回转拟合核估计方法(SBK)，该方法在弱相依条件下是oracally有效的，可用于分析高维时间序列。Dominici (2002)等人 [6] 将广义可加模型应用在环境污染对健康影响研究中。Zou (2016)等 [7] 使用广义可加模型和典型线性土地利用回归(LUR)模型估计PM2.5浓度，对比结果表明广义可加模型在年度和季节尺度上都优于LUR模型，广义可加模型的调整R2更高，RMSES更低。

可加Logistic模型是广义可加模型的一种特殊情况，常用于解决分类问题：

$\ln (\frac{μ}{1 - μ}) = \sum_{j = 1}^{p} f_{j} (X_{j}) + α$ (2)

其中， $μ = P (Y = 1)$ ，响应变量Y服从 $B (1, μ)$ ， $X_{j}$ 为协变量， $f_{j} (\cdot)$ 为未知函数，为保证模型的可识别性，满足 $E (f_{j} (\cdot)) = 0$ ， $α$ 为常数项。

Berg (2007) [8] 将可加Logistic模型用于破产预测，通过样本外和时间外验证表明广义可加模型在所有风险水平上都显著优于线性判别分析、广义线性模型和神经网络等流行模型。张娟和张贝贝(2016) [9] 使用半参数可加logistic模型对用户违约概率进行建模，并使用Group LASSO方法进行变量选择，实证研究表明该模型与线性Logistic回归模型相比，在判别能力和计算效率上均有较大优势。Dlamini等人(2017) [10] 使用可加Logistic模型研究与坦桑尼亚五岁以下儿童死亡率相关的风险因素，以指导决策者加快为人民提供更好的生活。Ana等人(2019) [11] 基于局部线性估计使用Logistic模型，对高血压病例进行建模分析。方匡南和陈子岚(2020) [12] 提出了一种基于半监督可加Logistic回归的信用评分模型，并应用于个人信用贷款的违约风险评估中。

本文余下内容安排如下：第2节介绍对可加Logistic模型的估计方法。第3节和第4节分别进行数值模拟和实证分析，比较可加Logistic模型和Logistic模型的表现。第5节进行相关理论性质的证明。第6节对全文进行总结。

2. 估计方法

对于Logistic模型，采用的是极大似然法求解模型中的参数，即通过最大化以下的对数似然函数得到参数 $β$ 的估计：

$l (β) = \sum_{i = 1}^{n} [y_{i} X_{i}^{T} β - \log (1 + e^{X_{i}^{T} β})]$

其中， $y_{i}$ 为响应变量， $X_{i}$ 为协变量， $β$ 为待估参数，n为样本量。 $l (β)$ 是关于 $β$ 的高阶可导连续凸函数，需采用一些数值方法求得最优解 $β^{*} = \arg \max_{β} {l (β)}$ 。

对于可加Logistic模型，仍采用极大似然法，此时目标函数变为：

$Q (β) = \sum_{i = 1}^{n} [y_{i} \sum_{j = 1}^{p} f_{j} (x_{i j}) - \log (1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i j})})]$ (3)

其中， $y_{i}$ 为响应变量， $f_{j} (\cdot)$ 为未知函数，n为样本量。

要求解(3)式，首先需对未知函数 $f_{j} (\cdot)$ ， $j = 1, \dots, p$ 进行估计。本文采取的是B样条近似，其样条基函数形式如下：

$B_{i, d} (x) = \frac{x - ν_{i}}{ν_{i + d} - ν_{i}} B_{i, d - 1} (x) + \frac{ν_{i + d + 1} - x}{ν_{i + d + 1} - ν_{i + 1}} B_{i + 1, d - 1} ( x )$

且

$B_{i, 0} (x) = {\begin{array}{l} 1, if ν_{i} \leq x \leq ν_{i + 1} \\ 0, Otherwise \end{array}$

其中，d为多项式次数， $ν_{i}$ 称为节点。

设 $ν = (ν_{1}, \dots, ν_{k})$ 为节点向量，其中 $a \leq ν_{1} \leq \dots \leq ν_{k} \leq b$ 为协变量范围 $[a, b]$ 上的节点，k为节点个数； $φ (x) = (φ_{1} (x), \dots, φ_{K_{n}} (x))$ 为d次B样条基函数，其中 $K_{n} = d + k$ 。令 ${\bar{φ}}_{j w} (x) = \frac{1}{n} \sum_{i = 1}^{n} φ_{w} (x_{i j})$ ， $B_{j w} (x) = φ_{w} (x) - {\bar{φ}}_{j w}$ ，其中 $j = 1, \dots, p$ ； $w = 1, \dots, K_{n}$ ，则 $f_{j} (X_{j})$ 可用B样条函数近似，即：

$f_{j} (X_{j}) \approx B_{j} (X_{j}) β_{j}$

其中， $β_{j} = {(β_{j 1}, \dots, β_{j K_{n}})}^{T}$ ， $B_{j} (X_{j}) = (B_{j 1} (X_{j}), \dots, B_{j K_{n}} (X_{j}))$ 。则模型(2)可写为：

$\ln (\frac{μ}{1 - μ}) \approx \sum_{j = 1}^{p} B_{j} (X_{j}) β_{j} + α$ (4)

令 $β = {(β_{1}^{T}, \dots, β_{p}^{T}, α)}^{T}$ ， $B (x) = (B_{1} (X_{1}), \dots, B_{p} (X_{p}), B_{0})$ ，其中 $α$ 为常数项， $B_{0} = {(1, \dots, 1)}_{n \times 1}^{T}$ ， ${(y_{i}, x_{i}), i = 1, \dots, n}$ 为样本，则(4)式可进一步简化表达为：

$\ln (\frac{μ}{1 - μ}) = B (x) β$ (5)

目标函数(3)式可写为：

$Q (β) = \sum_{i = 1}^{n} [y_{i} B (x_{i}) β - \log (1 + e^{B (x_{i}) β})]$ (6)

通过最大化目标函数(6)式可得到 $β$ 的估计 $\hat{β}$ ，则未知函数 $f_{j} (\cdot)$ 的估计为：

${\hat{f}}_{j} (X_{j}) = B_{j} (X_{j}) {\hat{β}}_{j}, j = 1, \dots, p$

采用拟牛顿法来求解(6)式中的 $β$ 的估计值，过程如下：

Step 1：取初始值 $β_{0}$ ，初始n阶阵 $H_{0}$ 。令 $k = 0$ 。

Step 2：计算 $g_{k} = \frac{\partial Q (β_{k})}{\partial β_{k}}$ ， $d_{k} = - H_{k} g_{k}$ 。令 $β_{k + 1} = β_{k} + α d_{k}$ ，其中，步长 $α$ 由线搜索产生。若 $‖ g_{k + 1} ‖ \leq 10^{- 6}$ ，算法停止：否则，转Step 3。

Step 3：令 $H_{k + 1} = H_{k} + \frac{(s_{k} - H_{k} y_{k}) {(s_{k} - H_{k} y_{k})}^{T}}{{(s_{k} - H_{k} y_{k})}^{T} y_{k}}$ ， $k = k + 1$ ，转Step 2。

这里的线搜索方法，采用Armijo步长规则：取 $α_{k} = β γ^{m_{k}}$ ，其中， $m_{k}$ 为满足下式的最小非负整数m：

$f (x_{k} + β γ^{m_{k}} d_{k}) \leq f (x_{k}) + σ β γ^{m_{k}} g_{k}^{T} d_{k}$

其中， $β > 0$ ， $σ, γ \in (0, 1)$ 。

3. 数值模拟

考虑生成符合(7)式的模拟数据：

$E (y_{i}) = \frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i j}) + α}}{1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i j}) + α}}, i = 1, 2, \dots, n$ (7)

$p_{i} = \frac{1}{1 + \exp (- \sum_{j}^{4} f_{j} (x_{i j}) + ε_{i})}$

其中， $f_{1} (x) = - 2 \sin (2 x)$ ， $f_{2} (x) = x^{2} - 25 / 12$ ， $f_{3} (x) = x$ ， $f_{4} (x) = \exp (- x) - 2 \sinh (5 / 2) / 5$ ，协变量 $X_{j} ~ U (- 2.5, 2.5)$ ， $y_{i} ~ B (1, p_{i})$ ， $ε_{i} ~ N (0, 1)$ ，n为样本量。

使用第2节提到的方法估计 $f_{j} (\cdot)$ ， $j = 1, 2, 3, 4$ 。考虑3种不同样本量的模拟数据集 ${(x_{i}, y_{i})}_{i = 1}^{n}$ ， $n = 200, 500, 800$ 。对模拟数据分别建立可加Logistic模型(GAM)和Logistic模型(GLM)，得到不同样本量下这2种模型的函数拟合图，见图1。以MSE指标评估函数估计的准确性，重复产生N = 100组数据集，计算4种函数估计的平均MSE，结果记录于表1；同时以查准率P、查全率R及F1为指标评价分类正确率，计算N组数据集的平均P、R、F1值，结果记录于表2。

$M S E_{j} = \frac{1}{N} \sum_{m = 1}^{N} [\frac{1}{n} \sum_{i = 1}^{n} {({\hat{f}}_{j}^{(m)} (x_{i j}) - f_{j}^{(m)} (x_{i j}))}^{2}], j = 1, \dots, p$

$P = \frac{1}{N} \sum_{m = 1}^{N} \frac{T P^{(m)}}{T P^{(m)} + F P^{( m )}}$

$R = \frac{1}{N} \sum_{m = 1}^{N} \frac{T P^{(m)}}{T P^{(m)} + F N^{( m )}}$

$F 1 = \frac{2}{1 / P + 1 / R} = \sum_{m = 1}^{N} \frac{2 T P^{(m)}}{2 T P^{(m)} + F P^{(m)} + F N^{( m )}}$

其中，N表示重复实验次数，TP、FN、FP、TN分别表示4种预测情况的样本数量：TP表示真正例样本数；FN表示假反例样本数；FP表示假正例样本数；TN表示真反例样本数。MSE越小，表明函数拟合得

(a1) (b1) (c1) (a2) (b2) (c2)

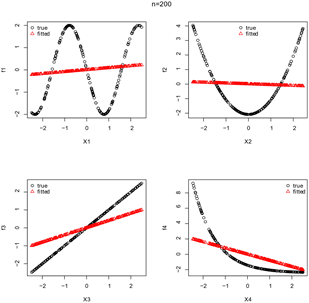
Figure 1. (a1), (b1) and (c1) are the function fitting graphs of GAM; (a2), (b2) and (c2) are the function fitting graphs of GLM

图1. (a1)、(b1)、(c1)为GAM的函数拟合图；(a2)、(b2)、(c2)为GLM的函数拟合图

Table 1. MSE values fitted by two models

表1. 2种模型拟合的MSE值

越好；P、R和F1是二分类问题常用指标，这3个指标越大，说明模型的预测效果越好。

由图1可直观地看出2种模型对每个函数 $f_{j} (\cdot), j = 1, 2, 3, 4$ 的拟合效果，可明显看出，在变量间存在非线性关系时，使用可加Logistic模型比使用Logistic模型能更好的拟合函数，这一点可进一步通过表1和表2中的数值来说明。

表1的数值结果显示，3种不同的样本量下，通过可加Logistic模型得到的函数估计误差值均比通过Logistic模型得到的函数估计误差值小，这表明在变量存在非线性关系时，通过可加Logistic模型能得到更精确的估计。且随着样本量的增加，通过两种模型得到的函数估计误差都在减小，这表明样本量越大，估计越精确。

Table 2. Classification accuracy under two models

表2. 2种模型下的分类正确率

表2的数值结果显示，3种不同的样本量下，无论是训练集还是测试集上，通过可加Logistic模型得到的P、R和F1值均比通过Logistic模型得到的P、R和F1值大，这表明在变量间存在非线性关系时，可加Logistic模型较Logistic模型能得到更高的分类正确率。

4. 实证分析

选取鲭鱼卵密度数据集进行实例分析，该数据集记录了对欧洲西北部海岸附近的鲭鱼卵丰度进行的调查，可通过R语言获取。变量描述见表3：

Table 3. Variable description of mackerel egg density dataset

表3. 鲭鱼卵密度数据集的变量描述

以Density为响应变量，其余变量为协变量。Density = 0.00时赋值为0，表示该位置不存在鲭鱼，Density > 0.00时赋值为1，表示该位置存在鲭鱼。赋值后有108个样本对应的响应变量为1309个样本对应的响应变量为0，为得到平衡数据样本，将响应变量为1的样本复制3次后，与309个响应变量为0的样本组成新的数据集，共633个样本。对新数据集的协变量进行函数估计，得到图2所示的函数估计图。

Figure 2. Function estimation graph of mackerel egg density data set

图2. 鲭鱼卵密度数据集的函数估计图

图2描绘了鲭鱼卵密度数据集的5个协变量函数估计结果，由此可看出协变量对于响应变量的影响是非线性的，因此可知建立可加Logistic模型是合适的。为进一步说明当变量间存在非线性关系时，Logistic模型不能很好的进行判别，对鲭鱼卵密度数据分别建立可加Logistic模型和Logistic模型。对数据集进行100次测试集和训练集的划分，以P、R和F1值为评价指标，对比两种模型在训练集和测试集上的评价指标平均值，结果见表4。

Table 4. Classification accuracy of mackerel egg density data set under two models

表4. 鲭鱼卵密度数据集在2种模型下的分类正确率

表4的数值结果显示，使用可加Logistic模型在训练集和测试集上的P、R和F1值都高于使用Logistic模型得到的P、R和F1值，这表明使用可加Logistic模型能得到更高的分类精度。

综上，由模拟数据和实际数据可知，当事先无法确定数据服从的模型形式时，使用非参数模型能得到更正确的结论和更高的精度。

5. 主要定理及证明

假设下列条件成立：

C1： $E (f_{j} (X_{j})) = 0$ ， $j = 1, 2, \dots, p$ 。

C2：假设 $X_{j}$ 的密度函数是 $g_{X_{j}} (\cdot)$ ，并且存在两个常数 $c_{1}$ 和 $c_{2}$ 在区间 $[a, b]$ 满 $0 < c_{1} \leq g_{X_{j}} (x) \leq c_{2} < \infty$ 足， $j = 1, 2, \dots, p$ 。

C3：令d是非负整数，且满足 $0 < d < r - 1$ ， $r \geq 2$ 。定义在区间 $[a, b]$ 上的函数 $f_{j}$ ，其d阶导数满足条件 $η \in (0, 1]$ ，即对 $d + η \geq 0.5$ ， $s, t \in [a, b]$ 有 $| f_{j}^{(d)} (t) - f_{j}^{(d)} (s) | \leq c {| t - s |}^{η}$ ， $j = 1, 2, \dots, p$ ，其中c是正的有限常数。

注：条件C1~C3是多项式样条估计的一般性假设，见Huang [13] 等，Guo [14] 等。

引理1：在条件C1~C3的假定下，模型(5)的参数真实值为 $β^{*}$ ，则 $f_{j}^{*} = B_{j} (X_{j}) β_{j}^{*}$ 。对任意的 $f_{j}$ 有：

$‖ f_{j}^{*} - f_{j} ‖ = O_{p} (K_{n}^{- r} + K_{n}^{1 / 2} n^{- 1 / 2}), j = 1, \dots, p$

特别的，当节点数 $K_{n} = O (n^{1 / (2 r + 1)})$ 时，

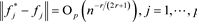
证明过程参见Huang [13] 。

引理2：定义 $D = \frac{1}{n} \sum_{i = 1}^{n} B^{T} (x_{i}) B (x_{i})$ ， $λ_{\min} (D)$ 和 $λ_{\max} (D)$ 分别是D的最小和最大特征值， $K_{n} = O (n^{v})$ ，其中 $0 < v < 0.5$ ，且 $h \equiv h_{n} ≍ K_{n}^{- 1}$ ，在条件C1~C2下，以概率1成立，有：

$c_{3} h_{n} \leq λ_{\min} (D) \leq λ_{\max} (D) \leq c_{4} h_{n}$

其中， $c_{3}$ 和 $c_{4}$ 两个正的常数。

证明过程参见Wei [15] 。

定理1：在条件C1~C3下，存在 ${\hat{f}}_{j} (X_{j}) = B_{j} (X_{j}) {\hat{β}}_{j}$ ，当 $K_{n} \to \infty$ ， $K_{n} / n \to 0$ 时，有下式成立：

$‖ {\hat{f}}_{j} - f_{j} ‖ = O_{p} (K_{n}^{- r} + K_{n}^{1 / 2} n^{- 1 / 2})$

特别地， $K_{n} = O (n^{1 / (2 r + 1)})$ 时，有：

$‖ {\hat{f}}_{j} - f_{j} ‖ = O_{p} (n^{- r / (2 r + 1)})$

定理1的证明过程见附录。

6. 结论

本文对可加Logistic模型中的非参数函数部分使用B样条逼近，结合极大似然思想，得到函数的估计，并在一定条件下，证明了该估计量的最优收敛速度。通过对模拟数据和实际数据分别建立可加Logistic模型和Logistic模型，对比MSE、P、R和F1的指标值，结果表明可加Logistic模型得到的MSE值更小，P、R和F1值更大，这说明在变量间存在非线性关系时，可加Logistic模型较Logistic模型能得到更好的估计和更高的分类正确率。

文章引用

昝思吕. 基于B样条的可加Logistic模型估计
Estimation of Additive Logistic Model Based on B-Spline[J]. 理论数学, 2024, 14(02): 612-623. https://doi.org/10.12677/PM.2024.142060

参考文献

1. Hastie, T.J. and Tibshirani, R.J. (1990). Generalized Additive Models. Chapman and Hall, New York. https://doi.org/10.1201/9780203753781-6

2. Horowitz, J.L. and Mammen, E. (2004) Nonparametric Estima-tion of an Additive Model with a Link Function. The Annals of Statistics, 32, 2412-2443. https://doi.org/10.1214/009053604000000814

3. Alimadad, A. and Salibian-Barrera, M. (2011) An Outli-er-Robust Fit for Generalized Additive Models with Applications to Disease Outbreak Detection. Journal of the American Statistical Association, 106, 719-731. https://doi.org/10.1198/jasa.2011.tm09654

4. Wood, S.N. (2008) Fast Stable Direct Fitting and Smoothness Selection for Generalized Additive Models. Journal of the Royal Statistical Society Series B: Statistical Methodology, 70, 495-518. https://doi.org/10.1111/j.1467-9868.2007.00646.x

5. Liu, R., Yang, L. and Härdle, W.K. (2013) Oracally Effi-cient Two-Step Estimation of Generalized Additive Model. Journal of the American Statistical Association, 108, 619-631. https://doi.org/10.1080/01621459.2013.763726

6. Dominici, F., McDermott, A., Zeger, S.L. and Samet, J.M. (2002) On the Use of Generalized Additive Models in Time-Series Studies of Air Pollution and Health. American Journal of Epidemiology, 156, 193-203. https://doi.org/10.1093/aje/kwf062

7. Zou, B., Chen, J., Zhai, L., Fang, X. and Zheng, Z. (2016) Satellite Based Mapping of Ground PM2.5 Concentration Using Generalized Additive Modeling. Remote Sensing, 9, 1. https://doi.org/10.3390/rs9010001

8. Berg, D. (2007) Bankruptcy Prediction by Generalized Additive Models. Applied Stochastic Models in Business and Industry, 23, 129-143. https://doi.org/10.1002/asmb.658

9. 张娟, 张贝贝. 基于Group-LASSO方法的广义半参数可加信用评分模型应用研究[J]. 数理统计与管理, 2016, 35(3): 517-524.

10. Dlamini, W.J., Melesse, S.F. and Mwambi, H.G. (2017) Logistic Regression Additive Model: Applica-tion to Tanzania Demographic and Health Survey Data. The Open Public Health Journal, 10, 294-302. https://doi.org/10.2174/1874944501710010294

11. Ana, E., Chamidah, N., Andriani, P. and Lestari, B. (2019) Modeling of Hypertension Risk Factors Using Local Linear of Additive Nonparametric Logistic Regression. Journal of Physics: Conference Series, 1397, Article 012067. https://doi.org/10.1088/1742-6596/1397/1/012067

12. 方匡南, 陈子岚. 基于半监督广义可加Logistic回归的信用评分方法[J]. 系统工程理论与实践, 2020, 40(2): 392-402.

13. Huang, J., Horowitz, J.L. and Wei, F. (2010) Variable Selection in Nonparametric Additive Models. Annals of Statistics, 38, 2282-2313. https://doi.org/10.1214/09-AOS781

14. Guo, J., Tang, M., Tian, M. and Zhu, K. (2013) Variable Selection in High-Dimensional Partially Linear Additive Models for Composite Quantile Regression. Computational Statistics & Data Analysis, 65, 56-67. ttps://doi.org/10.1016/j.csda.2013.03.017

15. Wei, F. (2012) Group Selection in High-Dimensional Partially Linear additive Models. Brazilian Journal of Probability and Statistics, 26, 219-243. https://doi.org/10.1214/10-BJPS129

附录

定理1的证明：根据引理1可知 $R = \sum_{j = 1}^{p} [f_{j}^{*} (x_{i j}) - f_{j} (x_{i j})] = O_{p} (K_{n}^{- r} + K_{n}^{1 / 2} n^{- 1 / 2})$ 。

为证定理1的结论，需先证：

$‖ \hat{β} - β^{*} ‖ = O_{p} (K_{n}^{- (2 r - 1) / 2} + K_{n} / \sqrt{n}) ≜ O_{p} (δ)$ (8)

令 $β = β^{*} + δ u$ ，u为 $p K_{n}$ 维向量。为证(8)式成立，需证对任意给定的 $ε$ ，存在足够大的常数C，使得下式成立：

$P {\sup_{‖ u ‖ = C} Q (β) < Q (β^{*})} \geq 1 - ε$ (9)

因为(9)式成立，意味着至少以 $1 - ε$ 的概率在球 ${β^{*} + δ u : ‖ u ‖ \leq C}$ 中存在一个局部最大值。因此，存在一个局部最大值使得 $‖ \hat{β} - β^{*} ‖ = O_{p} (δ)$ 。

对目标函数的表达式使用泰勒展开：

$\begin{matrix} Q (β) = \sum_{i = 1}^{n} [y_{i} B (x_{i}) β - \log (1 + e^{B (x_{i}) β})] \\ = \sum_{i = 1}^{n} [y_{i} B (x_{i}) (β^{*} + δ u) - \log (1 + e^{B (x_{i}) (β^{*} + δ u)})] \\ 在 B (x_{i}) β^{*} 处展开 \\ = \sum_{i = 1}^{n} {y_{i} [B (x_{i}) β^{*} + B (x_{i}) δ u + o {(B (x_{i}) δ u)}^{2}] \begin{matrix} \end{matrix} \\ - [\log (1 + e^{B (x_{i}) β^{*}}) + \frac{e^{B (x_{i}) β^{*}}}{1 + e^{B (x_{i}) β^{*}}} B (x_{i}) δ u + \frac{1}{2} \frac{e^{B (x_{i}) β^{*}}}{{(1 + e^{B (x_{i}) β^{*}})}^{2}} {(B (x_{i}) δ u)}^{2}] + o {(B (x_{i}) δ u)}^{2}} \end{matrix}$

则有：

$\begin{matrix} Q (β) - Q (β^{*}) = \sum_{i = 1}^{n} {y_{i} B (x_{i}) δ u - \frac{e^{B (x_{i}) β^{*}}}{1 + e^{B (x_{i}) β^{*}}} B (x_{i}) δ u - \frac{1}{2} \frac{e^{B (x_{i}) β^{*}}}{{(1 + e^{B (x_{i}) β^{*}})}^{2}} {(B (x_{i}) δ u)}^{2} + o {(B (x_{i}) δ u)}^{2}} \\ ≜ I_{1} + I_{2} + o {(B (x_{i}) δ u)}^{2} \end{matrix}$ (10)

其中， $I_{1} = \sum_{i = 1}^{n} [y_{i} - \frac{e^{B (x_{i}) β^{*}}}{1 + e^{B (x_{i}) β^{*}}}] B (x_{i}) δ u$ ； $I_{2} = - \frac{1}{2} δ^{2} u^{T} \sum_{i = 1}^{n} [\frac{e^{B (x_{i}) β^{*}}}{{(1 + e^{B (x_{i}) β^{*}})}^{2}} \cdot B {(x_{i})}^{T} B (x_{i})] u$ 对 $I_{1}$ 在 $\sum_{j = 1}^{p} f_{j} (x_{i})$ 处泰勒展开，有：

$I_{1} = n \frac{1}{n} \sum_{i = 1}^{n} [y_{i} - \frac{e^{B (x_{i}) β^{*}}}{1 + e^{B (x_{i}) β^{*}}}] B (x_{i}) δ u = n \frac{1}{n} \sum_{i = 1}^{n} [y_{i} - \frac{e^{R + \sum_{j = 1}^{p} f_{j} (x_{i})}}{1 + e^{R + \sum_{j = 1}^{p} f_{j} (x_{i})}}] B (x_{i}) δ u$

$= n \frac{1}{n} \sum_{i = 1}^{n} [y_{i} - \frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i})}}{1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i})}} - \frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i})}}{{(1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i})})}^{2}} R + o (R)] B (x_{i}) δ u$

令 $W_{1} = \frac{1}{n} \sum_{i = 1}^{n} [y_{i} - \frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i})}}{1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i})}} - \frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i})}}{{(1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i})})}^{2}} R] B (x_{i}) u$ ，则有：

$\begin{matrix} E (W_{1}) = \frac{1}{n} \sum_{i = 1}^{n} E {[y_{i} - \frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i})}}{1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i})}} - \frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i})}}{{(1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i})})}^{2}} R] B (x_{i})} u \\ = - \frac{1}{n} \sum_{i = 1}^{n} E [\frac{e^{\sum_{j = 1}^{p} f_{j} (x_{i})}}{{(1 + e^{\sum_{j = 1}^{p} f_{j} (x_{i})})}^{2}} R B (x_{i})] u \\ \leq - \frac{C_{1}}{n} \sum_{i = 1}^{n} E [R B (x_{i})] u \\ \leq - C_{1} R ‖ u ‖ \sqrt{E [\frac{1}{n} \sum_{i = 1}^{n} B {(x_{i})}^{T} B (x_{i})]} \\ = - C_{1} ‖ u ‖ O_{p} (K_{n}^{- r} + K_{n}^{\frac{1}{2}} n^{- \frac{1}{2}}) O_{p} (\sqrt{K_{n}^{- 1}}) \\ = ‖ u ‖ O_{p} (K_{n}^{- (2 r + 1) / 2} + n^{- 1 / 2}) \end{matrix}$

即 $I_{1} = O_{p} (n δ (K_{n}^{(- 2 r - 1) / 2} + n^{- 1 / 2}) ‖ u ‖)$ 。

类似可得： $I_{2} = O_{p} (n δ^{2} K_{n}^{- 1} {‖ u ‖}^{2}) = O_{p} (n δ (K_{n}^{(- 2 r - 1) / 2} + n^{- 1 / 2}) {‖ u ‖}^{2})$ 。

因此，当C足够大时， $I_{2}$ 控制 $I_{1}$ ，即(10)式的符号取决于 $I_{2}$ 。因为 $I_{2} < 0$ ，所以 $Q (β) - Q (β^{*}) < 0$ ，因此(9)式成立，即： $‖ \hat{β} - β^{*} ‖ = O_{p} (K_{n}^{- (2 r - 1) / 2} + K_{n} / \sqrt{n})$ 成立。则，

$\begin{matrix} ‖ {\hat{f}}_{j} - f_{j} ‖ \leq ‖ {\hat{f}}_{j} - f_{j}^{*} ‖ + ‖ f_{j}^{*} - f_{j} ‖ \\ = ‖ B (x_{i}) {\hat{β}}_{j} - B (x_{i}) β_{j}^{*} ‖ + ‖ f_{j}^{*} - f_{j} ‖ \\ = ‖ {\hat{β}}_{j} - β_{j}^{*} ‖ \sqrt{B^{T} (x_{i}) B (x_{i})} + ‖ f_{j}^{*} - f_{j} ‖ \\ = O_{p} (K_{n}^{- (2 r - 1) / 2} + K_{n} / \sqrt{n}) O_{p} (\sqrt{K_{n}^{- 1}}) + O_{p} (K_{n}^{- r} + K_{n}^{1 / 2} n^{- 1 / 2}) \\ = O_{p} (K_{n}^{- r} + K_{n}^{1 / 2} n^{- 1 / 2}) \end{matrix}$

定理1证毕。

期刊菜单