Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20794,6
pages
10.12677/AAM.2017.63044
The Lower Bounds of the Interval Edge-Colorings of Infinite Bicyclic Graphs
Yanliang Tao
College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang

Received: May 6th, 2017; accepted: May 24th, 2017; published: May 27th, 2017

ABSTRACT
An edge-coloring of a graph G with colors 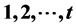 is an interval t-coloring, if all colors are used, and the colors of edges incident to each vertex of G are distinct and form an interval of integer. A graph G is interval colorable if it has an interval t-coloring for some positive integer t. The set of all interval colorable graphs is denoted by
is an interval t-coloring, if all colors are used, and the colors of edges incident to each vertex of G are distinct and form an interval of integer. A graph G is interval colorable if it has an interval t-coloring for some positive integer t. The set of all interval colorable graphs is denoted by . For a graph
. For a graph , the least and the greatest values of t for which G has an interval t -coloring are denoted by
, the least and the greatest values of t for which G has an interval t -coloring are denoted by 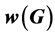 and
and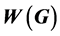 , respectively. In this paper, we show
, respectively. In this paper, we show  for any infinite bicyclic graph
for any infinite bicyclic graph .
.
Keywords:Interval Edge-Coloring, Lower Bound, Infinite Bicyclic Graph

无穷双圈图的区间边着色的下界
陶艳亮
新疆大学数学与系统科学学院,新疆 乌鲁木齐

收稿日期:2017年5月6日;录用日期:2017年5月24日;发布日期:2017年5月27日

摘 要
图G的一个用了颜色 的边着色称为区间t-着色,如果所有t种颜色都被用到,并且关联于G的同一个顶点的边上的颜色是各不相同的且这些颜色构成了一个连续的整数区间。图G称为是可区间着色的,如果对某个正整数t,G有一个区间t-着色。所有可区间着色的图构成的集合记作
的边着色称为区间t-着色,如果所有t种颜色都被用到,并且关联于G的同一个顶点的边上的颜色是各不相同的且这些颜色构成了一个连续的整数区间。图G称为是可区间着色的,如果对某个正整数t,G有一个区间t-着色。所有可区间着色的图构成的集合记作 。对图
。对图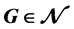 ,使得G有一个区间t-着色的t的最小值和最大值分别记作
,使得G有一个区间t-着色的t的最小值和最大值分别记作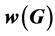 和
和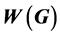 。本文中,我们证明了对于无穷双圈图
。本文中,我们证明了对于无穷双圈图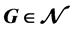 ,有
,有 。
。
关键词 :区间着色,下界,无穷双圈图

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文中讨论的图都是有限的,无向的,没有自环和重边的图。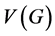 和
和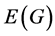 分别表示图
分别表示图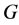 的顶点集和边集,
的顶点集和边集, 和
和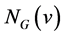 分别表示顶点
分别表示顶点 在图
在图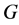 中的度和邻点集,
中的度和邻点集, 表示图
表示图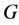 的最大度。
的最大度。
图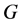 的一个顶点称为悬挂点,如果它的度等于1,
的一个顶点称为悬挂点,如果它的度等于1,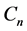 表示
表示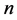 个顶点的圈。设
个顶点的圈。设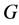 是一个连通图,
是一个连通图, 称为
称为 的圈数。当
的圈数。当 时,
时, 是双圈图。图
是双圈图。图 的一个真边着色是图
的一个真边着色是图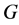 的一个边着色使得没有两条相邻边着相同的颜色。图
的一个边着色使得没有两条相邻边着相同的颜色。图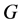 的边色数
的边色数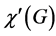 是图
是图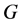 的所有真边着色中所用颜色的最小数目。如果
的所有真边着色中所用颜色的最小数目。如果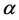 是图
是图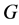 的一个真边着色,那么顶点
的一个真边着色,那么顶点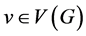 的谱,记作
的谱,记作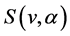 ,是与
,是与 关联的边上的颜色构成的集合。我们用
关联的边上的颜色构成的集合。我们用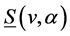 和
和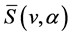 分别表示
分别表示 的谱的最小颜色和最大颜色。
的谱的最小颜色和最大颜色。
图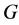 的一个用了颜色
的一个用了颜色 的真边着色称为区间t-着色,如果所有t种颜色都被用到,并且对于任意的
的真边着色称为区间t-着色,如果所有t种颜色都被用到,并且对于任意的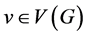 ,与顶点
,与顶点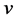 关联的边所着颜色的色值构成一个连续整数区间,即
关联的边所着颜色的色值构成一个连续整数区间,即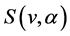 是一个连续整数区间。图
是一个连续整数区间。图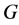 称为是可区间着色的,如果对某个正整数t,
称为是可区间着色的,如果对某个正整数t,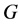 有一个区间t-着色。所有可区间着色的图构成的集合记作
有一个区间t-着色。所有可区间着色的图构成的集合记作 。对图
。对图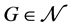 ,使得
,使得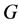 有一个区间t-着色的t的最小值和最大值分别记作
有一个区间t-着色的t的最小值和最大值分别记作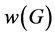 和
和 。显然,
。显然,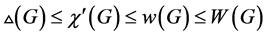 。
。
区间着色的概念是由Asratian和Kamalian在 [1] 中提出来的。在 [1] [2] 中,他们证明了如果 ,那么
,那么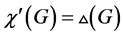 。对正则图来说,这个结论的逆也是成立的。此外,如果
。对正则图来说,这个结论的逆也是成立的。此外,如果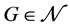 是一个正则图,那么
是一个正则图,那么 ,且对任意的
,且对任意的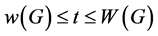 ,
,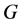 有一个区间t-着色。在 [3] 中,Kamalian进一步证明了如果
有一个区间t-着色。在 [3] 中,Kamalian进一步证明了如果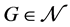 是一个连通图,那么
是一个连通图,那么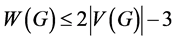 。这个上界被Giaro,Kubale和Malafiejski在 [4] 中改进了,他们证明了如果
。这个上界被Giaro,Kubale和Malafiejski在 [4] 中改进了,他们证明了如果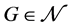 并且是一个至少有3个顶点的连通图,那么
并且是一个至少有3个顶点的连通图,那么 。对某些图类来说,
。对某些图类来说, 的上界还得到了进一步的改进。其中包括可平面图 [5] 和至少有
的上界还得到了进一步的改进。其中包括可平面图 [5] 和至少有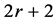 个顶点的r-正则图 [6] 。
个顶点的r-正则图 [6] 。
图的亏度,记作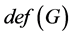 ,是指粘在
,是指粘在 上使得它可区间着色的悬挂边的最小数目。显然,
上使得它可区间着色的悬挂边的最小数目。显然,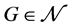 当且仅当
当且仅当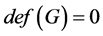 。在 [7] 中张维娟完全确定了单圈图和双圈图的亏度。参数
。在 [7] 中张维娟完全确定了单圈图和双圈图的亏度。参数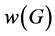 和
和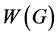 的确切数值对少数几类可区间着色的图来说已经完全确定了,其中包括偶圈,树 [8] 。本文中,我们完全确定了无穷双圈图
的确切数值对少数几类可区间着色的图来说已经完全确定了,其中包括偶圈,树 [8] 。本文中,我们完全确定了无穷双圈图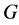 的下界,并且证明了
的下界,并且证明了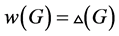 。
。
本文的框架如下。第二部分,给出了无穷双圈图的下界。第三部分,结论。第四部分,致谢。
2. 无穷双圈图的区间边着色的下界
图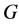 称作是无穷双圈无悬挂图,如果它恰有一个4度点其它顶点都是2度点,见图1所示。在无穷
称作是无穷双圈无悬挂图,如果它恰有一个4度点其它顶点都是2度点,见图1所示。在无穷

Figure 1. Infinite bicyclic graph without of pendent edge
图1. 无穷双圈无悬挂图
双圈无悬挂图 的顶点上不断添加悬挂边得到的图称作无穷双圈有悬挂图。用符号
的顶点上不断添加悬挂边得到的图称作无穷双圈有悬挂图。用符号 表示所有无穷双圈无悬挂图的集合,用符号
表示所有无穷双圈无悬挂图的集合,用符号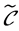 表示所有无穷双圈有悬挂图的集合。用
表示所有无穷双圈有悬挂图的集合。用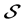 表示所有无穷双圈图的集合,显然有
表示所有无穷双圈图的集合,显然有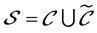 。
。
引理2.1 [7] 如果图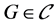 ,则有
,则有

引理2.2。如果 并且
并且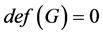 ,则
,则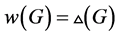 。
。
证明:设 的两个圈为
的两个圈为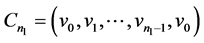 ,
,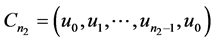 ,公共顶点为
,公共顶点为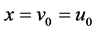 ,即
,即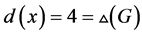 。由引理2.1知道
。由引理2.1知道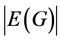 是偶数。又因为
是偶数。又因为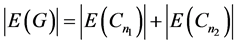 ,所以
,所以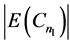 和
和 有相同的奇偶性。
有相同的奇偶性。
情况1。 和
和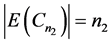 都是奇数。
都是奇数。
下面我们给出图 的一个区间4-着色
的一个区间4-着色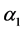 。我们给
。我们给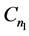 的边集:
的边集: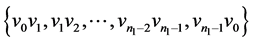 分别着色:
分别着色: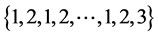 ,同时给
,同时给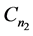 的边集:
的边集: 分别着色:
分别着色: ,就得到
,就得到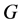 的一个区间4-着色
的一个区间4-着色 。
。
情况2。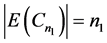 和
和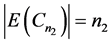 都是偶数。
都是偶数。
下面我们给出图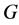 的一个区间4-着色
的一个区间4-着色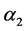 。我们给
。我们给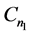 的边集:
的边集: 分别着色:
分别着色: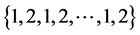 ,同时给
,同时给 的边集:
的边集: 分别着色:
分别着色: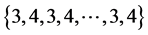 ,就得到
,就得到 的一个区间4-着色
的一个区间4-着色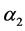 。
。
由以上讨论我们知道,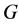 总有区间4-着色,因此,
总有区间4-着色,因此, 。另一方面,
。另一方面, 。所以得到
。所以得到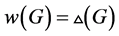 成立。
成立。
用符号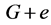 表示图
表示图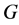 通过添加一条悬挂边
通过添加一条悬挂边 得到的图。
得到的图。
引理2.3。如果 并且
并且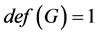 ,则
,则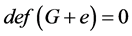 并且
并且 。
。
证明:设 的两个圈为
的两个圈为 ,
, ,公共顶点为
,公共顶点为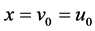 ,即
,即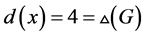 。由
。由 ,由引理2.1知道
,由引理2.1知道 是奇数。又因为
是奇数。又因为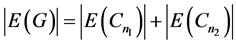 ,所以
,所以 和
和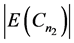 有不同的奇偶性。不失一般性,令
有不同的奇偶性。不失一般性,令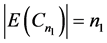 为奇数,,
为奇数,, 为偶数。当添加一条悬挂边
为偶数。当添加一条悬挂边 ,
,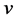 是悬挂点。由亏度的定义,得到
是悬挂点。由亏度的定义,得到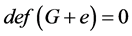 成立。
成立。
下面我们证明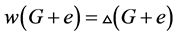 。
。
情况1。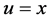 ,此时,
,此时,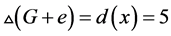 。我们给出图
。我们给出图 的一个区间5-着色
的一个区间5-着色 。我们给
。我们给 的边集:
的边集: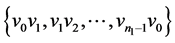 分别着色:
分别着色: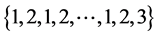 ,同时给
,同时给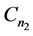 的边集:
的边集: 分别着色:
分别着色: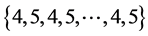 ,给边
,给边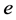 着颜色2,就得到
着颜色2,就得到 的一个区间5-着色
的一个区间5-着色 。
。
情况2。 ,此时,
,此时,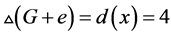 。我们给出图
。我们给出图 的一个区间4-着色
的一个区间4-着色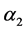 。如果
。如果 ,我们给
,我们给 的边集:
的边集: 分别着色:
分别着色: ,同时给
,同时给 的边集:
的边集: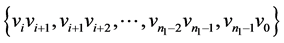 分别着色:
分别着色: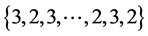 ,给
,给 的边集:
的边集: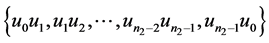 分别着色:
分别着色: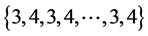 ,给边
,给边 着颜色2,就得到
着颜色2,就得到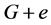 的一个区间4-着色
的一个区间4-着色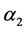 。如果
。如果 ,我们给
,我们给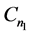 的边集:
的边集: 分别着色:
分别着色: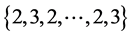 ,同时给
,同时给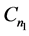 的边集:
的边集: 分别着色:
分别着色: ,给
,给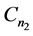 的边集:如果
的边集:如果 ,我们给
,我们给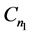 的边集:
的边集: 分别着色:
分别着色: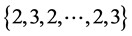 ,同时给
,同时给 的边集:
的边集: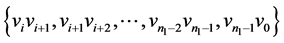 分别着色:
分别着色: ,给
,给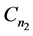 的边集:
的边集: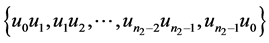 分别着色:
分别着色: ,给边
,给边 着颜色2,就得到
着颜色2,就得到 的一个区间4-着色
的一个区间4-着色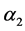 。分别着色:
。分别着色: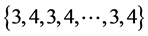 ,给边
,给边 着颜色2,就得到
着颜色2,就得到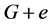 的一个区间4-着色
的一个区间4-着色 。
。
情况3。 ,此时,
,此时, 。我们给出图
。我们给出图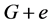 的一个区间4-着色
的一个区间4-着色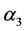 。如果
。如果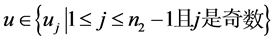 ,我们给
,我们给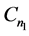 的边集:
的边集: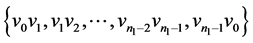 分别着色:
分别着色: ,给
,给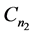 的边集:
的边集: 分别着色:
分别着色: ,同时给
,同时给 的边集:
的边集: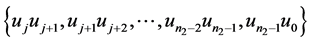 分别着色:
分别着色: ,给边
,给边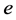 着颜色3,就得到
着颜色3,就得到 的一个区间4-着色
的一个区间4-着色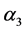 。如果
。如果 ,我们给
,我们给 的边集:
的边集: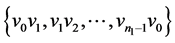 分别着色:
分别着色: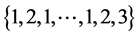 ,给
,给 的边集
的边集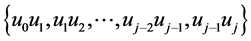 分别着色:
分别着色: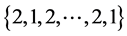 ,同时给
,同时给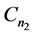 的边集:
的边集: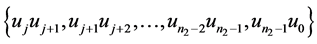 分别着色:
分别着色: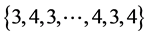 ,给边
,给边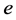 着颜色2,就得到
着颜色2,就得到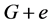 的一个区间4-着色
的一个区间4-着色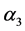 。
。
由以上讨论我们知道, 总有区间
总有区间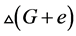 -着色,因此,
-着色,因此,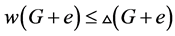 。另一方面,
。另一方面,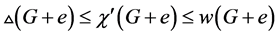 。我们得到:
。我们得到: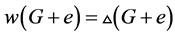 成立。
成立。
引理2.4。设 ,则
,则 。
。
证明:首先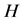 是由某个
是由某个 通过不断加悬挂边得到的图。其中
通过不断加悬挂边得到的图。其中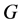 的两个圈为
的两个圈为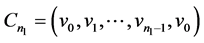 ,
,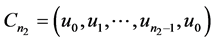 ,公共顶点为
,公共顶点为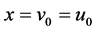 。因此
。因此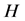 有悬挂边
有悬挂边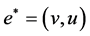 ,其中
,其中 为悬挂点。由引理2.2知道如果
为悬挂点。由引理2.2知道如果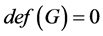 ,则
,则 有区间
有区间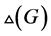 -着色
-着色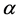 ,由引理2.3知道如果
,由引理2.3知道如果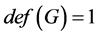 ,则
,则 并且
并且 也存在区间
也存在区间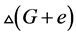 -着色。
-着色。
以下我们利用归纳法给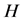 一个区间着色
一个区间着色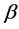 。设
。设 ,分别讨论以下几种情形。
,分别讨论以下几种情形。
如果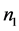 和
和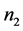 都是奇数,
都是奇数,
当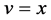 时,令
时,令
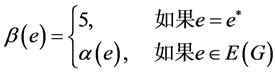
此时, 是一个区间5-着色。
是一个区间5-着色。
当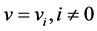 时,令
时,令

此时, 是一个区间4-着色。
是一个区间4-着色。
当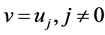 时,令
时,令
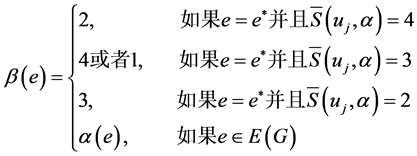
此时,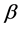 是一个区间4-着色。总之,
是一个区间4-着色。总之, 是
是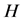 的一个区间
的一个区间 -着色。
-着色。
如果 和
和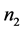 都是偶数,用类似的方法也可以得到
都是偶数,用类似的方法也可以得到 的一个区间
的一个区间 -着色,不妨也记作
-着色,不妨也记作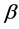 。
。
如果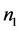 和
和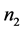 的奇偶性不同,则由引理2.3,图
的奇偶性不同,则由引理2.3,图 也存在区间
也存在区间 -着色,不妨也记作
-着色,不妨也记作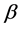 。
。
现在假设无穷双圈图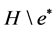 含有真子图
含有真子图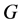 ,按归纳假设
,按归纳假设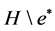 有区间着色
有区间着色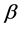 ,且它的区间边色数为
,且它的区间边色数为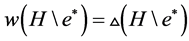 。以下要利用
。以下要利用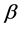 构造
构造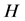 的一个区间
的一个区间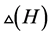 -着色
-着色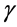 。我们考虑以下情形:
。我们考虑以下情形:
如果 的端点
的端点 是
是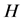 的最大度点,即
的最大度点,即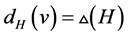 。此时,
。此时,
于是可取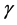 如下:
如下:
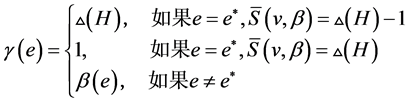
此时, 显然是
显然是 的一个区间
的一个区间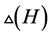 -着色。
-着色。
如果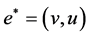 的端点
的端点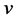 不是
不是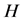 的最大度点,即
的最大度点,即 。此时
。此时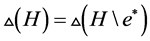 ,则我们可取
,则我们可取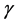 如下:
如下:

由于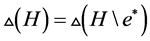 ,
,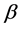 是一个
是一个 -连续着色,故
-连续着色,故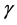 也是。由以上讨论,
也是。由以上讨论,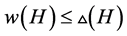 。另一方面,总有
。另一方面,总有 。于是结论成立,证毕。
。于是结论成立,证毕。
由引理2.2,2.3,2.4直接得到下面的结果。
3. 结论
设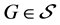 ,
,
(i) 如果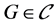 且
且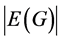 为奇数,那么
为奇数,那么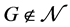 且
且 。
。
(ii)否则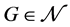 且
且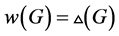 。
。
致谢
本文是在黄琼湘教授细心和认真的指导下完成的,在这里向黄老师表达深深的感谢和崇高的敬意。
文章引用
陶艳亮. 无穷双圈图的区间边着色的下界
The Lower Bounds of the Interval Edge-Colorings of Infinite Bicyclic Graphs[J]. 应用数学进展, 2017, 06(03): 382-387. http://dx.doi.org/10.12677/AAM.2017.63044
参考文献 (References)
- 1. Asratian, A.S. and Kamalian, R.R. (1987) Interval Colorings of Edges of a Multigraph. Applied Mathematics, 5, 25-34. (In Russian)
- 2. Asratian, A.S. and Kamalian, R.R. (1994) Investigation on Interval Edge-Colorings of Graphs. Journal of Combinatorial Theory, Series B, 62, 34-43.
- 3. Kamalian, R.R. (1990) Interval Edge Colorings of Graphs. Doctoral Thesis, Novosibirsk.
- 4. Giaro, K., Kubale, M. and Malafiejski, M. (2001) Consecutive Colorings of the Edges of General Graphs. Discrete Mathematics, 236, 131-143.
- 5. Axenovich, M.A. (2002) On Interval Colorings of Planar Graphs. Congressus Numerantium, 159, 77-94.
- 6. Kamalian, R.R. and Petrosyan, P.A. (2012) A Note on Interval Edge-Colorings of Graphs. Mathematical Problems of Computer Science, 36, 13-16.
- 7. Zhang, W.J. (2006) Consecutive Colorings of the Edges of Unicyclic and Bicyclic Graphs. Journal of Xinjiang University (Natural Science Edition), 23, 20-24.
- 8. Kamalian, R.R. (1989) Interval Colorings of Complete Bipartite Graphs and Trees, Preprint. Computer Center of the Academy, Sciences of Armenian SSR, Erevan. (In Russian)