Pure Mathematics
Vol.08 No.04(2018), Article ID:25592,7
pages
10.12677/PM.2018.84044
Meromorphic Function and Their Distribution of Zeros
Jianhao Lu, Li Chen
School of Mathematics and Computational Science, Wuyi University, Jiangmen Guangdong

Received: Jun. 4th, 2018; accepted: Jun. 19th, 2018; published: Jun. 27th, 2018

ABSTRACT
In this paper, we study zeros of difference product
and the value distribution of difference product
under the condition of
is a transcendental meromorphic function of finite order, where
, c is a Non-zero constant such that
.
Keywords:Transcendental Meromorphic Function, Difference Polynomials, Small Functions
亚纯函数及其差分乘积的零点分布
陆健豪,陈莉
五邑大学数学与计算科学学院,广东 江门

收稿日期:2018年6月4日;录用日期:2018年6月19日;发布日期:2018年6月27日

摘 要
本文主要研究
为有限级超越亚纯函数时,差分乘积
的零点情况以及
的值分布情况,此处
,c为任意非零常数满足
。
关键词 :超越亚纯函数,差分多项式,小函数

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言与定理
本文使用了Nevanlinna值分布论中常用记号及其基本结论 [1] 。本文出现的“亚纯函数”表示在整个复平面上亚纯。另外本文使用
表示亚纯函数f的增长级,
表示亚纯函数f的零点收敛指数,
表示亚纯函数f的极点收敛指数,记
,c为任意非零常数使得
。
Hayman在 [2] 中证明了下面定理。
定理A 若f为一个超越整函数且
,则
可取所有非零复常数无限多次。
2007年Laine和Yang在 [3] 中研究Hayman定理的差分形式的时候得出以下定理。
定理B 设
为有限级超越整函数,c为一非零复常数,则对于所有的
,
可取所有非零值a无限多次。
我们知道
能够看成
的差分形式,因此
的差分形式也可以看成
,因此
这一类差分乘积得到了数学家们的关注,其中Chen在 [4] 研究差分乘积
的零点情况时得到以下定理。
定理C 设
为有限级超越整函数,c为任意非零复常数使得
。
令
,
为整数。则以下结论成立
1) 若
具有无数多个零点,或者满足
,则
有无数多个零点。
2) 若
仅有有限多个零点并且满足
,则
仅有有限多个零点。
本文将上述定理的“整函数”条件推广到“亚纯函数”,得到以下定理。
定理1 设
为极点收敛指数
的超越亚纯函数,c为任意非零复常数使得
。
,
为整数。则以下结论成立
1) 若
具有无数多个零点,或者满足
,则
有无数多个零点。
2) 若
仅有有限多个零点并且满足
,则
仅有有限多个零点。
同时Chen在[4]中也考虑到差分乘积
当
即
的值分布情况,并得到以下定理。
定理D
为有限级超越整函数,且具有Borel例外值d,c为任意非零复常数使得
。函数集
,则以下结论成立
1)
可取任何非零复常数a无穷多次且满足
。
2) 若
,则
无有限的Borel例外值。
3) 若
,则0也是
的Borel例外值,从而
无有限非零的Borel例外值。
定理E
为有限级超越整函数,c为任意非零复常数使得
。令
,则以下结论成立
1) 若
仅有有限多个零点且满足
,或者
具有无穷多个零点,则
有无数多个零点。
2) 若
仅有有限多个零点并且满足
,则
仅有有限多个零点。
本文将定理D、E中的整函数推广到亚纯函数得到如下定理。
定理2 设
为具有两个Borel例外值
的有限级超越亚纯函数,c为任意非零复常数使得
。令
,则以下结论成立
1)
可取任何非零复常数a无穷多次且满足
。
2) 若
,则
无有限的Borel例外值。
3) 若
,则0也是
的Borel例外值,从而
无有限非零的Borel例外值。
定理3 设
为极点收敛指数
的超越亚纯函数,c为任意非零复常数使得
。令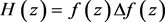 ,则以下结论成立
,则以下结论成立
1) 若
仅有有限多个零点且满足
,或者
具有无穷多个零点,则
有无数多个零点。
2) 若
仅有有限多个零点并且满足
,则
仅有有限多个零点。
最后,根据Borel例外值的定义,“
为具有两个Borel例外值
的有限级超越亚纯函数”等价于
,
。
2. 引理
本文定理的证明需要用到下述引理。
引理1 [5] 设
为差分方程
,的一个非常数有限级亚纯解,此处
为f的差分多项式,其系数
为亚纯函数,令
,若关于f及其平移的差分多项式
的次数至多是n,则有
对所有的r除去一个关于r的可能存在的具有有限对数测度的例外集成立。
引理2 [6] 设
为亚纯函数,
为整函数且满足
1)
;
2) 当
时,
不是常数;
3) 当
时,
,
为具有有限线性测度或有限对数测度的集合。则有
。
引理3 [7] 设
为非常数有限级亚纯函数,对
,有
引理4 [7] 设
为极点收敛指数
的超越亚纯函数,c为任意非零复常数,则对
有
引理5 设
为极点收敛指数
的超越亚纯函数,c为任意非零复常数,令
,则
。
证明:
(2.1)
由(2.1)以及引理3、4可得
于是
这意味着
。接下来证明
。
由(2.1)以及引理3、4也可得
由
得,
。
因此
。从而,
结论成立。
3. 定理1的证明
证明:1) 因为
为超越亚纯函数且
,从而当
有无穷多个零点时,
具有无穷多个零点。
现假设
仅有有限多个零点且
。又因为
为超越亚纯函数,故
能写成以下形式
(3.1)
此处
为多项式,
为整函数满足
,
为
极点的典型乘积,因此
。显然
。
由(3.1)可得
。因此
(3.2)
由引理5及
为超越函数,可得
为超越函数,故
能表示成如下形式
(3.3)
此处
为多项式,
为整函数满足
,
为
极点的典型乘积,因此
。显然
。
由(3.2) (3.3)可得
(3.4)
假设
,此处
为常数,由
可知
。因此
,此处
为常数。
由
可知
,故
不为常数。
若
和
都不为常数,则由引理2及(3.4)可得
。这是矛盾的。
若
,b为非零常数。即
,因此(3.4)可变为
(3.5)
由(3.5)及引理2可得
。这也是矛盾的。
若
为常数,则可由同样的方法得到矛盾。因此可得
有无穷多个零点。
2) 假设
仅有有限多个零点且
。则
可写成如下形式
(3.6)
此处
为常数,
为多项式,
为
极点的典型乘积,因此
。显然
。
由(3.6)可得
因为
,所以
。又因为
,故
仅有有限多个零点。
4. 定理2的证明
我们先证明第2)和3)。
2) 假设
,则
能写成如下形式。
(4.1)
此处a为非零常数,m为正整数,
为整函数满足
,
为
极点的典型乘积,因此
。显然
。因此
(4.2)
此处
为整函数,且满足
。由(4.1) (4.2)得
(4.3)
由
,可得
(4.4)
由(4.3) (4.4)可得
为有限级超越亚纯函数,且满足
。
若
有Borel例外值
,则
可表示成如下形式。
(4.5)
此处b为非零常数,m为正整数,
为整函数满足
,
为
极点的典型乘积,因此
。
。
由(4.3) (4.5)可得
(4.6)
若
且
,则由引理2和(4.6)可得
这是矛盾的。
若
或
,则利用定理1中得出(3.5)式的方法也可以推出矛盾。因此,
无有限的Borel例外值,(2)证明完毕。
下证(3),若
为
的Borel例外值,利用同样的方法由(4.3)可得
(4.7)
因为
且
,所以0为
的Borel例外值,从而
再无非零有限的Borel例外值。
最后证明1),由2) 3)可知若
有有限的Borel例外值,则任何非零有限值a必不为
的Borel例外值。因此
可取a无穷多次,因此可得
。
5. 定理3的证明
1) 因为
为亚纯函数且
,所以当
有无穷多个零点时
也有无穷多个零点。
现假设
有有限多个零点且
,因此
能写成如下形式
(5.1)
此处
为多项式,
,
为多项式,
为
极点的典型乘积,因此
。显然
。
由(5.1)可得
。因此
(5.2)
由引理5及
为超越函数,可得
为超越函数,故
能表示成如下形式
(5.3)
此处
为多项式,
为整函数满足
,
为
极点的典型乘积,因此
。显然
。
由(5.2) (5.3)可得
(5.4)
若
和
都不为常数,则由引理2及(5.4)可得
,
,
。这是矛盾的。
若
或
为常数,则用证明定理1的方法也可以得到矛盾结论。因此
有无穷多个零点。
2) 假设
仅有有限多个零点且
。则用证明定理1中证明2)的方法也可以得出结论。因此定理3证明完毕。
基金项目
广东省自然科学基金资助项目(2016A030313002),广东高校特色创新项目(2016KTSCX145)。
文章引用
陆健豪,陈 莉. 亚纯函数及其差分乘积的零点分布
Meromorphic Function and Their Distribution of Zeros[J]. 理论数学, 2018, 08(04): 333-339. https://doi.org/10.12677/PM.2018.84044
参考文献
- 1. 仪洪勋, 杨重骏. 亚纯函数唯一性理论[M]. 北京: 科学出版社, 1995.
- 2. Hayman, W.K. (1959) Picard Values of Meromorphic Functions and Their Derivatives. Annals of Mathematics, 70, 9-42. https://doi.org/10.2307/1969890
- 3. Laine, I. and Yang, C.C. (2007) Value Distribution of Difference Polynomials. Proceedings of the Japan Academy, Series A, Mathematical Sciences, 83, 148-151. https://doi.org/10.3792/pjaa.83.148
- 4. Chen, Z.X. (2011) Value Distribution of Products of Meromorphic Functions and Their Differences. Taiwanese Journal of Mathematics, 15, 1411-1421. https://doi.org/10.11650/twjm/1500406353
- 5. Chen, Z.X. (2014) Complex Differences and Difference Equations. Mathematics Monograph Series 29. Science Press, Beijing.
- 6. Yang, C.C. and Yi, H.X. (2003) Uniqueness Theory of Meromorphic Functions. Kluwer Academic Publishers Group, Dordrecht, 79-80. https://doi.org/10.1007/978-94-017-3626-8
- 7. Chiang, Y.M. and Feng, S.J. (2008) On the Nevanlinna Characteristic of and Difference Equations in the Complex Plane. The Ramanujan Journal, 16, 105-129. https://doi.org/10.1007/s11139-007-9101-1


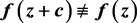





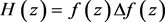 ,则以下结论成立
,则以下结论成立