Applied Physics
Vol.
09
No.
09
(
2019
), Article ID:
32279
,
6
pages
10.12677/APP.2019.99046
Chaotic Characteristic of Rossler System Based on Parametric Randomization
Haimei Zhou1, Wenhui Yu1,2, Mengqi Ma1, Shilong Gao1,3*
1College of Mathematics and Information Science, Leshan Normal University, Leshan Sichuan
2College of Science, Xihua University, Chengdu Sichuan
3Research Centre of Applied Mathematics, Leshan Normal University, Leshan Sichuan

Received: Sep. 3rd, 2019; accepted: Sep. 16th, 2019; published: Sep. 23rd, 2019

ABSTRACT
On the basis of the classical Rossler system, the system parameters are considered to take value in the chaotic interval and the non-chaotic interval according to a certain probability, and then the parameters randomized Rossler system is obtained. Numerical results show that chaotic phenomena still exist in Rossler system under random disturbance of parameters.
Keywords:Rossler System, Parameters Randomization, Chaos, Phase Diagrams
基于参数随机化的Rossler系统的混沌特征
周海梅1,余文慧1,2,马梦琪1,高仕龙1,3*
1乐山师范学院数学与信息科学学院,四川 乐山
2西华大学理学院,四川 成都
3乐山师范学院应用数学研究中心,四川 乐山

收稿日期:2019年9月3日;录用日期:2019年9月16日;发布日期:2019年9月23日

摘 要
在经典Rossler系统的基础上,考虑系统参数以一定的概率在混沌区间和非混沌区间取值,得到参数随机化的Rossler系统。数值结果表明,参数随机扰动下的Rossler系统仍然存在混沌现象。
关键词 :Rossler系统,参数随机化,混沌,相图

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
20世纪90年代,混沌和分岔理论的建立,为非线性动力学提供了科学的理论支撑。混沌作为大自然中普遍存在的一种现象,在现代科学的发展和进步中起着十分重要的作用。混沌现象的研究最早始于Lorenz,他在观察大气对流时无意间发现在确定性的非线性系统中存在混沌现象。自此以后,混沌现象开始在物理、生物、数学、通讯工程等领域有所了解和认识 [1] 。目前,混沌现象的研究及其应用非常广泛,已经渗透到自然科学的各个领域。
随着研究的不断深入,除了Lorenz系统以外,人们还发现了许多经典的混沌系统,Rossler系统就是其中的一个经典例子。德国物理化学家O.E.Rossler通过观察Lorenz吸引子的形成过程,发现从Lorenz吸引子中能够提取出一种非对称的、简单的吸引子结构 [2] ,这就是Rossler混沌系统。该混沌系统可由一个三维非线性微分方程组描述。关于Rossler系统的研究在混沌控制与同步方面已经较为成熟,目前研究的新方向是把Rossler系统应用于微弱周期信号的检测 [3] 和保密通信 [4] 等领域。
迄今为止,大多数学者对Rossler系统混沌特性的研究思路都是基于确定参数条件下,在定常数空间中进行数值模拟。例如,陕振沛用Matlab软件对Rossler混沌系统仿真、Lorenz系统再进行数值模拟,观察其相图、分岔图、混沌吸引子等动力特征 [5] ;刘健辰用其设计的反馈控制器实现了不同初值条件下Rossler系统的同步 [6] ;徐艳春讨论了在定常数空间下Rossler馄饨振子检测微弱信号的方法,并且验证了其有效性 [7] 。以上这些研究结果都是在定常空间下得到的,有研究表明,非确定参数下混沌系统的输出既具有混沌的不可预测性,又有不确定参数下的随机性,更利于保密通信的安全需要。因此,本文首先考虑对Rossler系统的参数进行随机化处理,并研究参数随机扰动下的Rossler系统的混沌特征。
2. Rossler系统
Rossler混沌系统是一个非线性系统,可以由下面确定的三维非线性方程组来描述:
(1)
其中a,b,c是系统的三个控制参数,x1,x2,x3是系统的状态变量。
通过求解如下方程
(2)
可得Rossler系统的平衡点为
(3)
当系统(1)的参数取 , , 时Rossler系统会产生混沌现象。图1为取定该参数下的Rossler混沌吸引子相图。

Figure 1. Chaotic attractor of Rossler system
图1. Rossler系统混沌吸引子
3. 算法与仿真分析
3.1. 参数b随机化
Rossler混沌系统的研究大多是基于定常参数条件下进行的。本文主要考虑将Rossler系统中某些参数按分布进行随机取值,再通过数值模拟,考察系统的混沌特征。
由系统(1)的分岔图2可知,在取定参数 , 的情况下,参数b有若干个混沌和非混沌区间。
对参数b进行随机化处理,即考虑如下的系统:
(4)
系统(4)的初始值取为 。随机变量 服从如下两点分布:
(5)
其中 在非混沌区间, 在混沌区间。求解方程组(4),数值模拟的结果如图3。

Figure 2. Bifurcation of Rossler system (1) versus parameter b
图2. Rossler系统(1)关于参数b的分岔图
观察图3中取不同概率值p时的相图,系统(4)具有以下明显的动力学行为:当 时,系统轨线收敛于稳定平衡点。当概率值p逐渐减小,系统相图表现为从单倍周期慢慢渐变为多倍周期,周期轨道逐渐稀疏。当 时,相图出现倍化的分岔序列 [8] ,进而继续演化直到进入混沌状态,形成了较为稳定的混沌轨道,即Rossler混沌吸引子。并伴随一部分窄带中存在的类似轨迹族,具备嵌套的、自相似结构 [9] 。上述动力学特征表明,参数随机化下的Rossler系统也可以由倍周期分岔后进入混沌的。
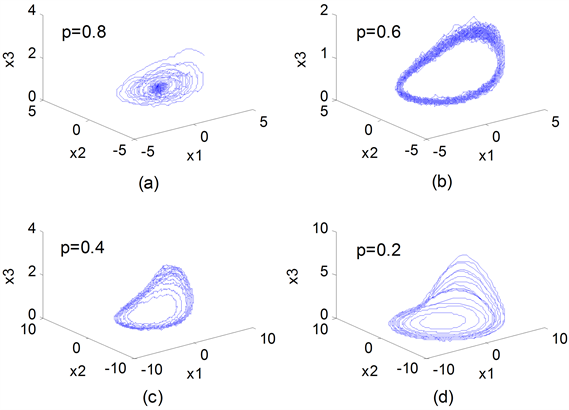
Figure 3. Phase diagrams of Rossler system at random parameter b
图3. 参数b随机化下Rossler系统的相图
3.2. 参数a,b随机化
根据分岔图4可知,参数a也具有多个混沌和非混沌区间。取定参数 ,考虑同时对系统(1)中参数a和b进行随机化处理,即考虑如下系统
(6)
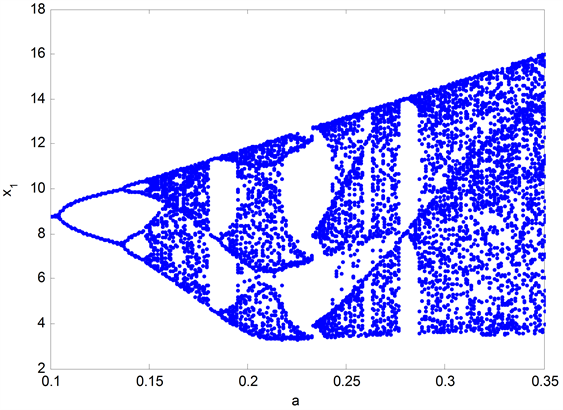
Figure 4. Bifurcation of Rossler system (1) versus parameter a
图4. Rossler系统(1)关于参数a的分岔图
系统(6)的初值依然为 。随机变是 和 在混沌区间和非混沌区间以相同的概率取值,即服从两点分布:
(7)
(8)
其中 和 分别在参数b和a的非混沌区间, 和 分别在参数b和a的混沌区间。求解方程组(6),实验结果如图5。
观察图5,此时系统(6)有如下动力学特征: 时,系统轨线收敛于稳定平衡点; 时,系统的运动轨线变密,体现为周期运动;随着非混沌区间的取值概率的减小, 时,系统开始逐渐出现倍周期分岔。在以上两个过程中,系统轨线除了体现为倍周期运动以外,轨线的随机性也比较明显。当 时,系统的运动轨线被吸引到了一个有限的相空间中 [10] ,这就是Rossler吸引子,此时系统呈现明显的混沌现象。

Figure 5. Phase diagrams of Rossler system at random parameter a and b
图5. 参数a和b随机化下Rossler系统的相图
4. 结论
本文研究了Rossler系统的控制参数a和b满足一定的分布条件下系统的混沌动力学特征。主要思路是将参数b或参数a在混沌区间和非混沌区间之间按一定的概率取值,从而达到将系统随机化的目的。数值模拟结果表明,随机参数控制下的Rossler系统依然可以产生混沌现象。
参数随机化的思想不仅仅适用于Rossler系统,对于其它一些混沌系统依然具有普适性和研究价值。同时,在后续研究中,可以进一步分析参数随机化下的Rossler系统在弱信号检测和保密通信等领域的应用。
基金项目
四川科技计划资助(NO: 2018JY0256);乐山师范学院2018年创新创业训练计划资助项目(NO: 201810649016)。
文章引用
周海梅,余文慧,马梦琪,高仕龙. 基于参数随机化的Rossler系统的混沌特征
Chaotic Characteristic of Rossler System Based on Parametric Randomization[J]. 应用物理, 2019, 09(09): 384-389. https://doi.org/10.12677/APP.2019.99046
参考文献
- 1. 周茜. 混沌理论及应用若干问题的研究[D]: [博士学位论文]. 天津: 南开大学, 2010.
- 2. 郭怡冰. Rossler混沌系统的混沌控制和研究[D]: [硕士学位论文]. 西安: 西安建筑科技大学, 2010.
- 3. 赵力, 史丽晨. 变形Rossler混沌及其在微弱信号检测的应用研究[J]. 计算机测量与控制, 2014, 22(2): 339-341.
- 4. 杨金玲. 参数不确定超混沌系统的同步研究[D]: [硕士学位论文]. 长春: 东北师范大学, 2012.
- 5. 陕振沛. 基于MATLAB的各类混沌系统的计算机仿真模拟研究[J]. 科技广场, 2015(6): 6-11.
- 6. 刘键辰. 分数阶Rossler混沌系统的模糊同步控制[J]. 信息与控制, 2008, 37(2): 130-134.
- 7. 徐艳春. 高阶混沌振子的微弱信号频率检测新方法[J]. 哈尔滨工业大学学报, 2010, 42(3): 447-450.
- 8. 尤小玲. Rossler系统的动力学行为研究及混沌抑制[J]. 工业仪表与自动化装置, 2013(4): 6-8.
- 9. 陈全发. 混沌动力系统中Rossler吸引子数值仿真分析[J]. 大学数学, 2009, 25(2): 52-55.
- 10. 赖宏慧. Rossler超混沌系统的混沌特性分析[J]. 江西理工大学学报, 2007, 28(4): 1-4.
NOTES
*通讯作者。