Material Sciences
Vol.07 No.04(2017), Article ID:21232,10
pages
10.12677/MS.2017.74058
A Study on Interfacial Shear Stress for Carbon Nanotube Composites
Ming Gao, Lichun Bian, Jing Pan, Wei Liu, Shurui Meng
Department of Engineering Mechanics, Yanshan University, Qinhuangdao Hebei

Received: Jun. 1st, 2017; accepted: Jun. 30th, 2017; published: Jul. 3rd, 2017

ABSTRACT
In this paper, the shear lag model is used to establish the representative element model of carbon nanotube composite and the carbon nanotube is considered as an effective fiber to simulate the main morphological characteristics of composites. The investigation focuses on the shear stress of interface, and it is assumed that the effective fibers and carbon nanotubes have the same diameter and length. The interface shear stress expression is derived using the continuity conditions of stress and displacement, and equilibrium equations. Based on the results obtained, the damage caused by the sliding displacement of carbon nanotube composites could be checked.
Keywords:Carbon Nanotube, Interfacial Shear Stress, Axial Loading, Shear Lag Model, Elastic Theory
碳纳米管复合材料的界面剪切应力研究
高明,卞立春,潘静,刘伟,孟淑睿
燕山大学,工程力学系,河北 秦皇岛
收稿日期:2017年6月1日;录用日期:2017年6月30日;发布日期:2017年7月3日

摘 要
本论文采用剪切滞后模型,建立了碳纳米管复合材料的代表性体元模型,并且将碳纳米管看做一个有效纤维,模拟分析碳纳米管复合材料的主要形态特性。研究重点主要集中在碳纳米管与基体接触面的剪切应力,假设有效纤维与碳纳米管具有相同的直径和长度,运用应力连续条件和位移连续条件以及相关平衡方程等,推导得出计算所需要的复合材料界面处的切应力表达式,本论文推论得到的结果可以校核碳纳米管复合材料因滑动位移而产生的破坏。
关键词 :碳纳米管,界面切应力,轴向应力,剪切滞后模型,弹性理论

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
碳纳米管(CNTs)具有较高的强度和刚度,许多科学家已经将碳纳米管看作是最终增强材料,并且认为其具有很好的发展方向 [1] 。一些研究表明,只要有1%(按重量)的碳纳米管添加在基体材料中,会使复合材料的刚度增加36%至42% [2] 。碳纳米管的承载能力在复合材料中也得到证实 [3] [4] [5] 。Ang和Ahmed [6] 及Li等 [7] 在Gao和Li [8] 的模型基础上建立了一种改进的剪切滞后模型,并且考虑了热残余应力和泊松收缩的影响。Wang等 [9] 研究了桥接法在碳纳米管增强复合材料拉出纤维接枝碳纳米管韧性分析中的应用,使用桥接法计算碳纳米管增强纳米复合材料的断裂韧性和预测碳纳米管接枝的常规短纤维的拉拔力位移响应。在考察了界面载荷传递对碳纳米管/聚合物复合材料应力分布以及弹性模量的影响方面,多尺度模型被广泛应用 [10] [11] [12] 。Banerjee等 [13] 及Lu和Hu [14] 采用有限元(FE)方法研究了纯碳纳米管和界面对玻璃状聚合物/单壁碳纳米管复合材料力学性能的影响。Chen等 [15] 在三级失效分析模型的基础上,研究了增强纤维在复合材料中的增韧效果。结果发现,较薄的增强纤维不一定赋予复合材料更好的断裂韧性。
近年来,剪切滞后模型和内聚力模型在碳纳米管增强复合材料界面特性进行研究中发挥了重要作用 [16] [17] [18] [19] 。自从1991年发现以来 [20] ,碳纳米管得到广泛的应用。尽管碳纳米管复合材料的研究取得了一些突破性进展,但是其实际应用仍然面临诸多困难和挑战。例如,碳纳米管复合材料的力学性能不稳定,并且在大多数情况下对基体性能的提高水平有限,远低于预测值,与传统的纤维增强复合材料的性能很难相比。因此,基于碳纳米管的应用研究需要探索新的发展途径。此外,基于碳纳米管的新型复合材料的制备仍然是一个困难和昂贵的过程。
本文研究对象采用单壁碳纳米管复合材料,研究单壁碳纳米管复合材料接触面的切应力和基体与纤维的轴向应力,来初步探讨在界面处不存在化学键的碳纳米管复合材料的破坏情况。本文进行理论上的推导,运用细观力学中的剪切滞后方法,建立研究对象模型。因为碳纳米管复合材料的代表性体元的应变相同,而两部分杨氏模量不同,因而产生不同的应力。据此来研究其接触面的切应力。本文的特色在于:运用剪切滞后模型,采用应力连续和位移连续双重条件来进行推导,进而简化了推导过程及表达式,以及进行了量化便于计算。
2. 碳纳米管复合材料应力分析
本文采用剪切滞后模型研究碳纳米管复合材料,研究重点集中在碳纳米管与基体的接触面的剪切应力。由于碳纳米管复合材料的两部分具有相同的应变,而拥有不同的杨氏模量,假设两部分均为线弹性,因此产生不同的正应力。在接触面上同时属于不同部分,故会产生应力差。有平衡方程知,剪应力为两应力差的一半。本文采用Gao和Li [8] 的模型,但从应力连续和位移连续两个方向出发,来探讨碳纳米管复合材料界面的切应力,如图1所示。
2.1. 理论推导
图1所示为Gao和Li [8] 中的剪切滞后模型代表性体元示意图,他们借助此模型进行了弹性理论分析,并得出了界面剪切应力和纤维轴向应力的封闭解,本文将延伸扩展此模型的分析计算。
本文只研究碳纳米管复合材料的加强区(即包含碳纳米管部分)的应力,如图2所示。
2.2. 加强区界面间的应力
代表体单元在不考虑体力,在极坐标下的位移平衡方程:
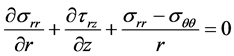 (1a)
(1a)
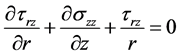 (1b)
(1b)
其中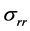 ,
, ,
,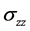 和
和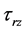 是应力变量。对平衡方程(1b),0到
是应力变量。对平衡方程(1b),0到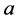 对
对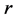 积分得:
积分得:
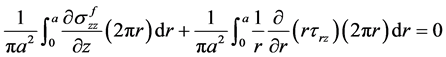 (3)
(3)
有效纤维平均应力定义为:
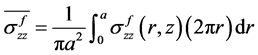 (4)
(4)
运用方程(4),方程(3)变为
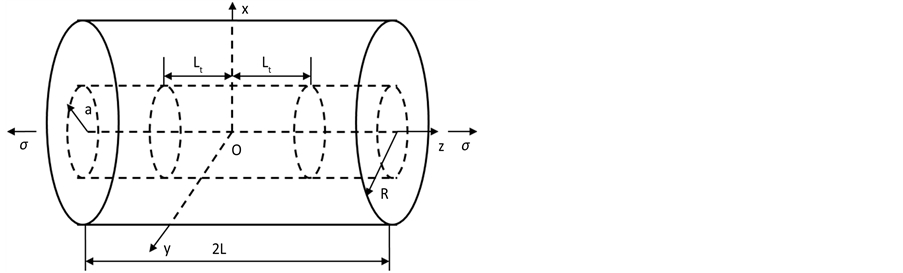
Figure 1. Diagram of the representative element of shear lag model
图1. 剪切滞后模型代表性体元示意图
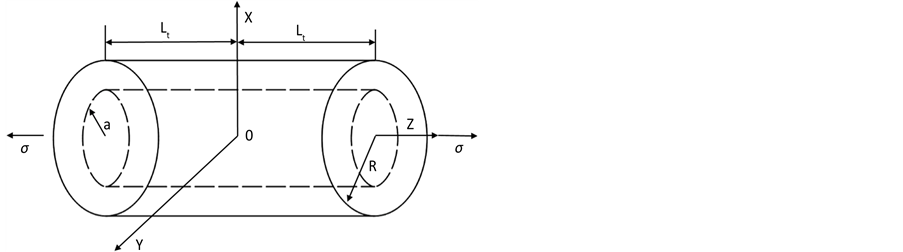
Figure 2. Cutting part of analysis model
图2. 所研究模型的截取部分
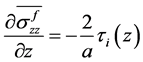 (5)
(5)
其中
 (6)
(6)
因为在模型的边缘假设不存在任何应力,即其应力大小为0。故其边界条件为:
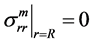 (7a)
(7a)
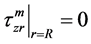 (7b)
(7b)
在碳纳米管复合材料中,界面处的正应力和切应力是连续的。因此边界连续条件为:
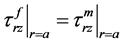 (8a)
(8a)
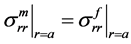 (8b)
(8b)
对平衡方程(1b)从a到R对r积分,并引入(6),(7 b),(8 b)得到以下表达式:
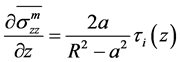 (9)
(9)
其中
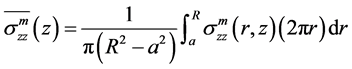 (10)
(10)
2.3. 计算界面的切应力
由于径向和环向应力与轴向应力相比是微不足道的,为了获得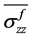 和
和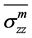 ,首先假设
,首先假设
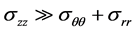 (11)
(11)
故有如下所示关系:
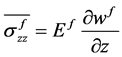 (12)
(12)
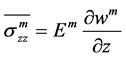 (13)
(13)
其中, 和
和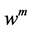 分别为碳纳米管和基体的轴向位移变量。由以上计算可以得出,如图3所示。
分别为碳纳米管和基体的轴向位移变量。由以上计算可以得出,如图3所示。
 (14)
(14)
 (15)
(15)
应用位移应变关系,故有如下方程:
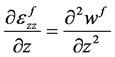 (16)
(16)
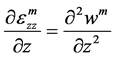 (17)
(17)

Figure 3. Diagram of stress equilibrium model
图3. 应力的平衡模型示意图
本构方程:
 (18)
(18)
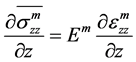 (19)
(19)
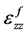 和
和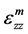 分别为纤维和基体的应变变量。如图3所示,为不使复合材料产生破坏,应力在模型的变化过程中不会产生突变,因为两部分有着不同的杨氏模量,相同的位移产生了不同的应力。而在模型中其应力连续。故应该由切应力来平衡两部分应力的差值。因此得到
分别为纤维和基体的应变变量。如图3所示,为不使复合材料产生破坏,应力在模型的变化过程中不会产生突变,因为两部分有着不同的杨氏模量,相同的位移产生了不同的应力。而在模型中其应力连续。故应该由切应力来平衡两部分应力的差值。因此得到
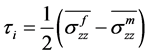 (20)
(20)
由方程(5) (9) (22)得
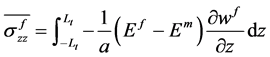 (21)
(21)
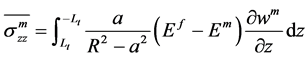 (22)
(22)
整理得
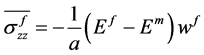 (23)
(23)
 (24)
(24)
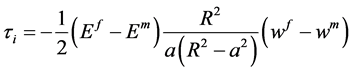 (25)
(25)
由公式(14)~(19)可以得出:
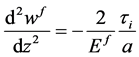 (26)
(26)
 (27)
(27)
其中,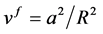 ,
,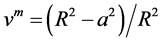 分别为碳纳米管和基体的体积分数。
分别为碳纳米管和基体的体积分数。
由公式(26)和(27)可以得出
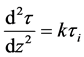 (28)
(28)
其中,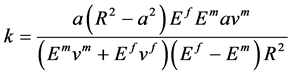 ,因此,求解上面的二阶微分方程可以推导出界面剪切应力的表达式为
,因此,求解上面的二阶微分方程可以推导出界面剪切应力的表达式为
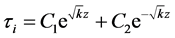 (29)
(29)
因此由公式(14)和(15)可以求得
 (30)
(30)
 (31)
(31)
在碳纳米管与基体接触的界面处,当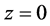 时,界面剪切应力为0,即
时,界面剪切应力为0,即
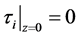 (32)
(32)
由公式(29)可知,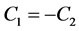 。另外,由考虑在z方向上复合材料的力平衡可知:
。另外,由考虑在z方向上复合材料的力平衡可知:
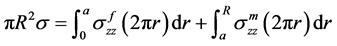 (33)
(33)
将公式(30)和(31)代入公式(33)中可以得出
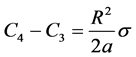 (34)
(34)
如果施加在纤维端部的边界条件为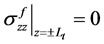 ,并且由公式(20)和(34)以及
,并且由公式(20)和(34)以及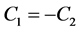 可以求得
可以求得
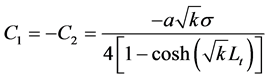 (35a)
(35a)
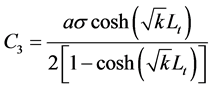 (35b)
(35b)
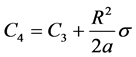 (35c)
(35c)
因此界面剪切应力以及施加在纤维和基体上的轴向应力为
 (36)
(36)
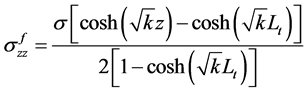 (37)
(37)
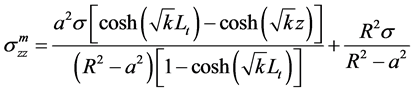 (38)
(38)
其中:
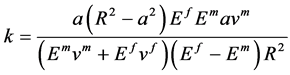 (39)
(39)
3. 讨论
为了说明在前面的部分中开发的剪切滞后模型,进行碳纳米管增强聚合物复合材料参数研究,使用新推导的公式,样本数值结果如下。为了便于比较,相关的材料参数取为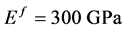 ,
,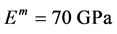 ,
,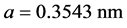 ,
,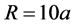 。图4和图5分别显示了复合材料纤维部分轴向应力和界面剪切应力分布情况。
。图4和图5分别显示了复合材料纤维部分轴向应力和界面剪切应力分布情况。
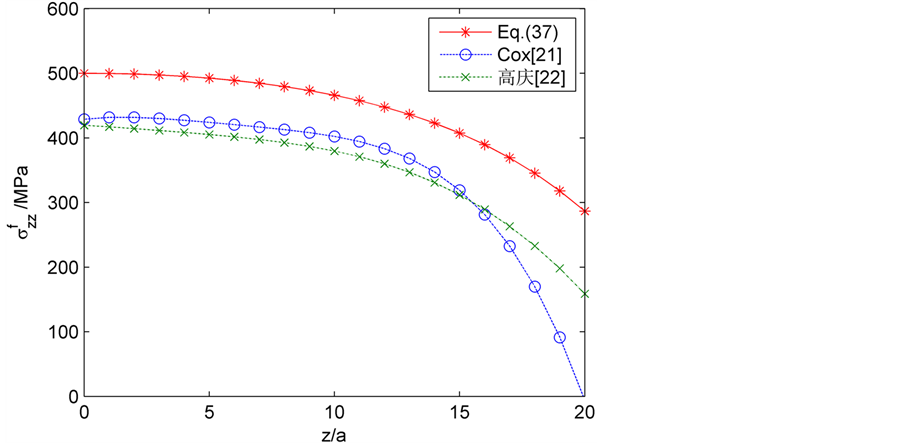
Figure 4. Distribution curve of fiber axial stress (AR = 12.8)
图4. 纤维轴向应力分布曲线(AR = 12.8)
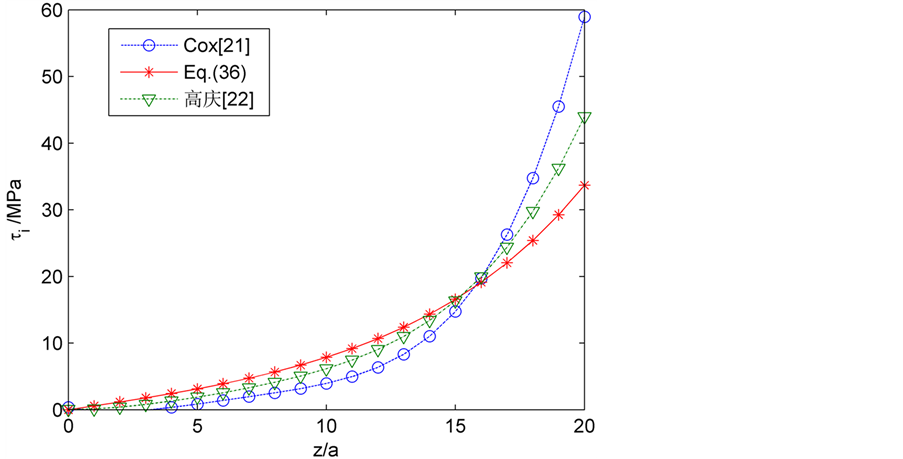
Figure 5. Distribution curve of interface shear stress (AR = 12.8)
图5. 界面剪切应力分布曲线(AR = 12.8)
本文新推导的公式的结果与Cox [21] 和高庆和康国政 [22] 的研究结果进行比较,由于在参数上略有差异,并且本文未考虑端部正应力的影响,即纤维端部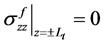 ,图5中显示的高庆和康国政 [22] 的曲线是在未考虑端面正应力情况所得出的公式(18)的模拟结果,可以看出,本文所得结果与其未考虑端面正应力所得结果比较吻合。轴向应力在结果比较上有一定的差异,这主要由于本文是考虑应力连续,没有考虑界面的影响,界面的模量和结合状态的变化不同,推导的公式就有变化,并且本文界面剪切应力由纤维和基体两部分的轴向应力平衡所得,所以对结果就会产生一定的影响,但总体趋势与高庆和康国政 [22] 的结果是一致的。另一方面,本文所推结果与Cox [21] 所得结果具有一定的差异,Cox [21] 研究所得理论
,图5中显示的高庆和康国政 [22] 的曲线是在未考虑端面正应力情况所得出的公式(18)的模拟结果,可以看出,本文所得结果与其未考虑端面正应力所得结果比较吻合。轴向应力在结果比较上有一定的差异,这主要由于本文是考虑应力连续,没有考虑界面的影响,界面的模量和结合状态的变化不同,推导的公式就有变化,并且本文界面剪切应力由纤维和基体两部分的轴向应力平衡所得,所以对结果就会产生一定的影响,但总体趋势与高庆和康国政 [22] 的结果是一致的。另一方面,本文所推结果与Cox [21] 所得结果具有一定的差异,Cox [21] 研究所得理论
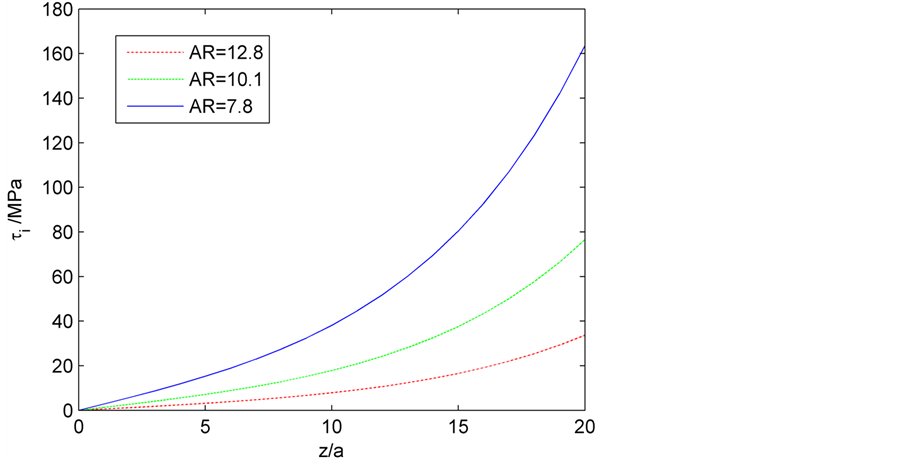
Figure 6. Distribution curve of interface shear stress under different length/diameter ratio
图6. 不同长径比下的界面剪切应力分布曲线
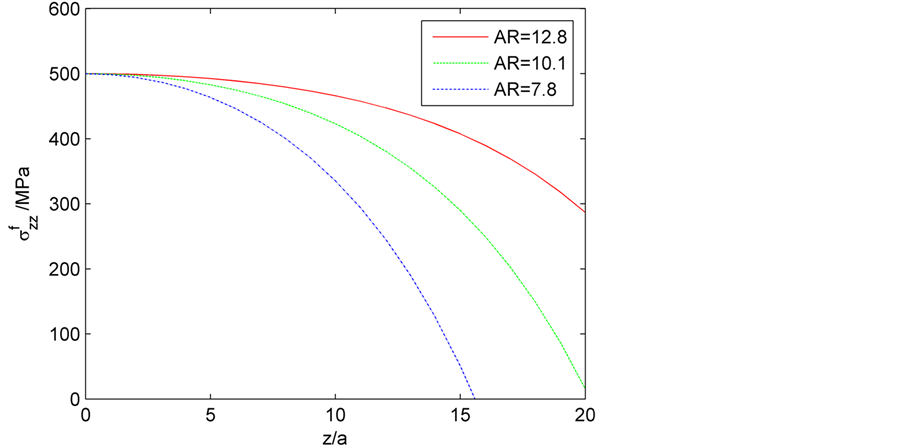
Figure 7. Distribution curve of fiber axial stress under different length/diameter ratio
图7. 不同长径比下的纤维轴向应力分布曲线
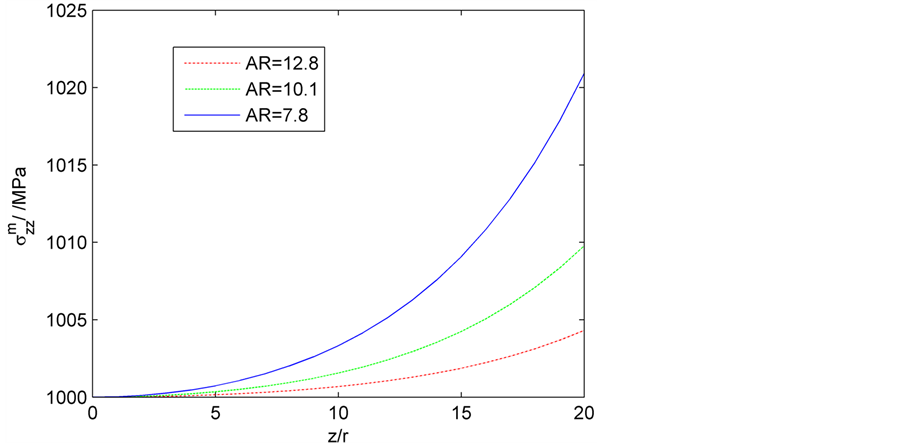
Figure 8. Distribution curve of matrix axial stress under different length/diameter ratio
图8. 不同长径比下的基体轴向应力分布曲线
只能考虑界面结合完好时的情况,并没有考虑端部正应力和界面的影响。
图6~图8所示图形为纤维和基体的轴向应力、界面剪切应力沿纳米管长度的变化曲线。从图6可以看出最大界面剪切应力发生在纳米管的末端,且中间的剪切应力具有对称性(在图中对称曲线没有标出)。此外,纵横比越大,纳米管的剪切应力越小(相同的z条件下)。图7和图8表示沿纳米管长度的纳米管的轴向正应力的分布和基体中的轴向正应力分布,显然他们也是对称曲线。从图7中观察到纤维最大轴向正应力在z = 0处,也就是说在纳米管中间,而最小发生在其两端。此外可以看出,纵横比越大,轴向应力越高。同样从图8可以看出基体最大轴向应力发生在端部,最小发生在z=0处,纵横比越大,轴向应力越低。
4. 结论
本文采用剪切滞后模型,建立了复合缸嵌入式碳纳米管复合材料代表性体元模型,将碳纳米管看做一个有效纤维,模拟碳纳米管复合材料的主要形态特性。其中,有效纤维与碳纳米管具有相同的直径和长度。运用弹性理论,应力连续条件及位移连续条件,推得了应力表达式,及界面处的切应力表达式,从碳纳米管复合材料的破坏条件和实验的测量条件来看,简化的表达式更容易实现。最大界面剪切应力发生在纳米管的末端,且中间的剪切应力具有对称性,纵横比越大,纳米管的剪切应力越小,此外可以看出,纵横比越大,轴向应力越高。本文考虑应力连续并且界面剪切应力由纤维和基体两部分的轴向应力平衡所得,总体趋势及在纤维端部界面剪切应力和纤维轴向应力与他人的结果比较吻合。
基金项目
河北省高等学校科学研究重点项目基金,编号:ZD2017075。
文章引用
高 明,卞立春,潘 静,刘 伟,孟淑睿. 碳纳米管复合材料的界面剪切应力研究
A Study on Interfacial Shear Stress for Carbon Nanotube Composites[J]. 材料科学, 2017, 07(04): 440-449. http://dx.doi.org/10.12677/MS.2017.74058
参考文献 (References)
- 1. Thostenson, E.T., Ren, Z.F. and Chou, T.W. (2001) Advances in the Science and Technology of Carbon Nanotubes and their Com-posites: A Review. Composites Science and Technology, 61, 1899-1912. https://doi.org/10.1016/S0266-3538(01)00094-X
- 2. Qian, D., Dickey, E.C., Andrews, R. and Rantell, T. (2000) Load Transfer and Deformation Mechanisms in Carbon Nanotube Polystyrene Composites. Applied Physics Letters, 76, 2868-2870. https://doi.org/10.1063/1.126500
- 3. Bian, L.C. and Zhao, H.C. (2015) Elastic Properties of a Single-Walled Carbon Nanotube under a Thermal Environment. Composite Structures, 121, 337-343. https://doi.org/10.1016/j.compstruct.2014.11.032
- 4. Wagner, H.D., Lourie, O., Feldman, Y. and Tenne, R. (1998) Stress-Induced Fragmentation of Multiwall Carbon Nanotubes in a Polymer Matrix. Applied Physics Letters, 72, 188-190.
- 5. 卞立春, 薛正敏, 潘静, 刘伟, 孟淑睿. 团聚效应碳纳米管复合材料特性分析[J]. 材料科学, 2016, 6(6): 398-406.
- 6. Ang, K.K. and Ahmed, K.S. (2013) An Improved Shear-Lag Model for Carbon Nanotube Reinforced Polymer Composites. Composites Part B Engineering, 50, 7-14. https://doi.org/10.1016/j.compositesb.2013.01.016
- 7. Li, W.X., Zhu, J., Hao, Y., Dai, J. and Wang, Q. (2010) A Shear-Lag Model for Carbon Nanotube-Reinforced Magnesium Matrix Composites. Advanced Materials And Processing, 15, 305-309.
- 8. Gao, X.L. and Li, K. (2005) A Shear-Lag Model for Carbon Nanotube-Reinforced Polymer Composites. International Journal of Solids and Structures, 42, 1649-1667. https://doi.org/10.1016/j.ijsolstr.2004.08.020
- 9. Wang, J.X., Tong, L. and Karihaloo, B.L. (2016) A Bridging Law and Its Application to the Analysis of Toughness of Carbon Nanotube-Reinforced Composites and Pull-Out of Fibres Grafted with Nanotubes. Archive of Applied Mechanics, 86, 361-373. https://doi.org/10.1007/s00419-015-1100-x
- 10. Pan, J., Bian, L.C., Zhao, H.C. and Zhao, Y. (2016) A New Micromechanics Model and Effective Elastic Modulus of Nanotube Reinforced Composites. Computational Materials Science, 113, 21-26. https://doi.org/10.1016/j.commatsci.2015.11.009
- 11. Alian, A.R., Kundalwal, S.I. and Meguid, S.A. (2015) Multiscale Modeling of Carbon Nanotube Epoxy Composites. Polymer, 7, 149-160.
- 12. Gupta, A.K. and Harsha, S.P. (2016) Analysis of Mechanical Properties of Carbon Nanotube Reinforced Polymer Composites Using Multi-Scale Finite Element Modeling Approach. Composites Part B. Engineering, 95, 172-178. https://doi.org/10.1016/j.compositesb.2016.04.005
- 13. Banerjee, D., Nguyen, T. and Chuang, T.J. (2016) Mechanical Properties of Single-Walled Carbon Nanotube Reinforced Polymer Composites with Varied Interphase’s Modulus and Thickness: A Finite Element Analysis Study. Computational Materials Science, 114, 209-218. https://doi.org/10.1016/j.commatsci.2015.12.026
- 14. Lu, X. and Hu, Z. (2012) Mechanical Property Evaluation of Single-Walled Carbon Nanotubes by Finite Element Modeling. Composites Part B. Engineering, 43, 1902-1913. https://doi.org/10.1016/j.compositesb.2012.02.002
- 15. Chen, Y., Wang, S., Liu, B. and Zhang, J. (2015) Effects of Geometrical and Mechanical Properties of Fiber and Matrix on Composite Fracture Toughness. Composite Structures, 122, 496-506. https://doi.org/10.1016/j.compstruct.2014.12.011
- 16. Liu, X., Yang, Q.S., He, X.Q. and Liew, K.M. (2016) Cohesive Laws for van der Waals Interactions of Super Carbon Nanotube/Polymer Composites. Mechanics Research Communications, 72, 33-40.
- 17. Jiang, L.Y., Huang, Y., Jiang, H., Ravichandran, G., Gao, H., Hwang, K.C. and Liu, B. (2006) A Cohesive Law for Carbon Nanotube/Polymer Interfaces Based on the van der Waals Force. Journal of the Mechanics and Physics of Solids, 54, 2436-2452. https://doi.org/10.1016/j.jmps.2006.04.009
- 18. Guo, G.D. and Zhu, Y. (2015) Cohesive-Shear-Lag Modeling of Interfacial Stress Transfer between a Monolayer Graphene and a Polymer Substrate. Journal of Applied Mechanics, 82, Article ID: 031005. https://doi.org/10.1115/1.4029635
- 19. Lu, W.B., Wu, J., Song, J., Hwang, K.C., Jiang, L.Y. and Huang, Y. (2008) A Cohesive Law for Interfaces between Multi-Wall Carbon Nanotubes and Polymers Due to the van der Waals Interactions. Computer Methods in Applied Mechanics & Engineering, 197, 3261-3267.
- 20. Iijima, S. (1991) Helical Microtubules of Graphitic Carbon. Nature, 354, 56-58. https://doi.org/10.1038/354056a0
- 21. Cox, H.L. (1952) The Elasticity and Strength of Paper and Other Fibrous Materials. British Journal of Applied Physics, 3, 72-79. https://doi.org/10.1088/0508-3443/3/3/302
- 22. 高庆, 康国政. 短纤维复合材料应力传递的修正剪滞理论[J]. 固体力学学报, 2000, 21(3): 198-204.