Advances in Applied Mathematics
Vol.
08
No.
06
(
2019
), Article ID:
30637
,
6
pages
10.12677/AAM.2019.86121
Lump Solutions to the (3+1)-Dimensional Mel’nikov Equation
Xiaoyu Li, Xuelin Yong*, Yehui Huang
School of Mathematical Sciences and Physics, North China Electric Power University, Beijing

Received: May 6th, 2019; accepted: May 28th, 2019; published: Jun. 4th, 2019

ABSTRACT
In this article, lump solutions of the (3+1)-dimensional Mel’nikov are obtained via the Hirota bilinear method and symbolic computation with Maple. A class of lump solutions rationally localized in all directions in the space is obtained. And we propose the conditions for the analyticity and rational localization of the lump solutions. By selecting special value of parameters involved, the dynamic characteristics of the solutions are illustrated.
Keywords:Lump Solution, (3+1)-Dimensional Mel’nikov, Hirota Bilinear Method
(3+1)维Mel’nikov方程的Lump解研究
李晓玉,雍雪林*,黄晔辉
华北电力大学数理学院,北京

收稿日期:2019年5月6日;录用日期:2019年5月28日;发布日期:2019年6月4日

摘 要
本文运用Hirota双线性方法和符号计算研究了(3+1)维Mel’nikov方程的Lump解。我们给出了一阶Lump解的表达式,并讨论了相应的解析性和局部性条件。最后,我们作出了解的图像并分析了解的动态性质。
关键词 :Lump解,(3+1)维Mel’nikov方程,Hirota双线性方法

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
作为孤子方程的可积推广,带自相容源的孤子方程是一类重要的数学物理模型,它涉及到流体力学、等离子体物理和固体物理中的很多问题 [1] 。带自相容源的孤子方程可以通过Sato理论 [2] ,反散射方法 [3] ,广义达布变换方法 [4] 和源生成法得到 [5] 。研究发现,在带自相容源的非线性可积系统中孤波是以变速度运动的 [6] - [11] 。
近年来在非线性科学中对于Lump波的研究引起了越来越多学者的广泛关注 [12] - [18] 。Lump解是一类局域的有理函数解,并且大量孤子方程的Lump解已经被找到 [19] [20] [21] [22] 。特别地,通过符号计算方法也给出了一些高维的非线性系统的有理解 [23] [24] [25] [26] [27] 。然而,对于(3+1)维的情况,得到的解往往不是在所有方向上都是局域有理化的,因此只能称为类Lump型解 [28] [29] [30] 。因此求解(3+1)维偏微分方程的Lump解是非常重要并且有意义的。
本文我们将研究如下的(3+1)维Mel’nikov方程:
(1)
文献 [31] 中通过Hirota方法和Wronskian技巧讨论了它的行列式解和双线性贝克隆变换。本文结构如下:在第二部分,通过变量变换并且利用Hirota双线性法得到了该方程的Lump解,同时作出了两组特解的图像并分析了它们的动力学性质。最后给出本文的结论。
2. Mel’nikov的Lump解
引入变量代换
(2)
方程(1)可以转化为如下双线性形式:
(3)
其中, 是实函数, 是关于 和 的复函数, 是 的复共轭函数。这里D是双线。
性算子定义如下 [32] :
(4)
为了求解双线性方程,我们作如下假设:
(5)
其中
(6)
这里的待定系数 全都是实数。
将(5)和(6)代入双线性方程(3)中,我们得到了一个包含自变量 和t的非线性方程组。将这些方程的系数分别取零后得到一个关于待定系数的超定代数方程组,利用Maple求解如下:
(7)
这里k是附加的实常数,需满足下列条件:
(8)
由此可以得到(3+1)维Mel’nikov方程的一类Lump解:
(9)
其中
(10)
且
(11)
在该Lump解中包含六个任意系数 。不失一般性,依据平移不变性我们可以设 或 。此外,对于任意给定时间t,在上述Lump解中 , 当且仅当对应的 ,或者换句话说,当 时, 。因此,条件 既保证了Lump解的解析性,又保证了Lump解的局域性。因此本文得到的解在空间所有方向上都是有理局域化的。为了获得更多的动力学性质,我们给定了一些参数值,并作出它们的二维和三维图像,如图1~4所示。
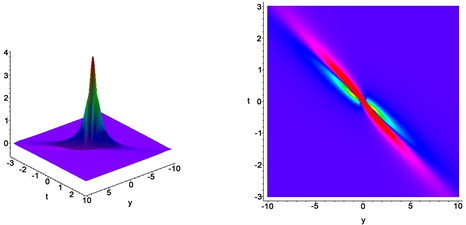
Figure 1. Plots of lump solution for u with when
图1. 当 , 时u的图像
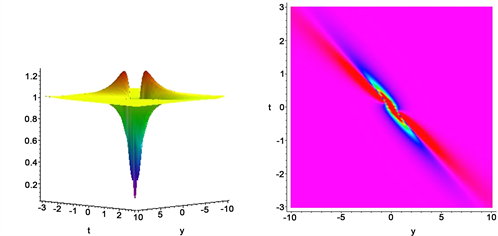
Figure 2. Plots of lump solution for with when
图2. 当 , 时 的图像
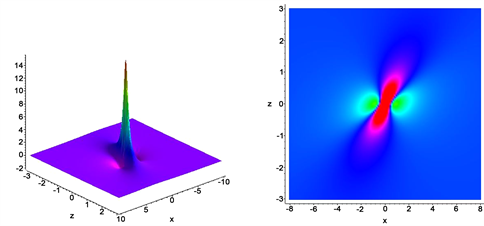
Figure 3. Plots of lump solution for u with when
图3. 当 , 时u的图像
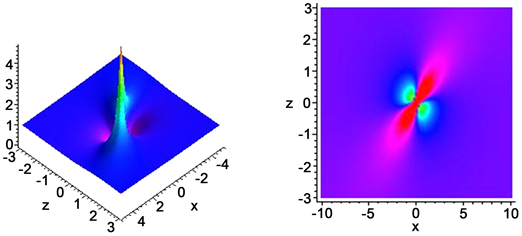
Figure 4. Plots of lump solution for with when
图4. 当 , 时 的图像
3. 结论
本文我们利用Hirota双线性方法给出了(3+1)维Mel’nikov方程的Lump解。通过作图我们观察到了方程更多的动力学性质。但是本文我们通过符号计算法仅得到了一阶Lump解,未来对于更高阶的解的研究将会是一个非常有意义的问题。
基金项目
本文工作受到了中央高校基本科研业务费(2019MS050)的资助。
文章引用
李晓玉,雍雪林,黄晔辉. (3+1)维Mel’nikov方程的Lump解研究
Lump Solutions to the (3+1)-Dimensional Mel’nikov Equation[J]. 应用数学进展, 2019, 08(06): 1058-1063. https://doi.org/10.12677/AAM.2019.86121
参考文献
- 1. Mel’Nikov, V.K. (1983) On Equations for Wave Interactions. Letters in Mathematical Physics, 7, 129-136. https://doi.org/10.1007/BF00419931
- 2. Lin, R.-L., Liu, X.-J. and Zeng, Y.-B. (2014) The KP Hierarchy with Self-Consistent Sources: Construction, Wronskian Solutions and Bilinear Identities. Journal of Physics: Conference Series, 538, Article No. 012014. https://doi.org/10.1088/1742-6596/538/1/012014
- 3. Lin, R.-L., Zeng, Y.-B. and Ma, W.-X. (2001) Solving the KdV Hierarchy with Self-Consistent Sources by Inverse Scattering Method. Physica A: Statistical Mechanics and Its Applications, 291, 287-298. https://doi.org/10.1016/S0378-4371(00)00519-7
- 4. Xiao, T. and Zeng, Y.-B. (2004) Generalized Darboux Transformations for the KP Equation with Self-Consistent Sources. Journal of Physics A: Mathematical and General, 37, 7143-7162. https://doi.org/10.1088/0305-4470/37/28/006
- 5. Wang, H.-Y. and Hu, X.-B. (2001) A Hybrid Type of Soliton Equations with Self-Consistent Sources: KP and Toda Cases. Journal of Mathematical Analysis and Applications, 376, 393-406. https://doi.org/10.1016/j.jmaa.2010.12.010
- 6. Zeng, Y.-B., Ma, W.-X. and Lin, R.-L. (2001) Integra-tion of the Soliton Hierarchy with Self-Consistent Sources. Journal of Mathematical Physics, 41, 5453-5489. https://doi.org/10.1063/1.533420
- 7. Deng, S.-F., Chen, D.-Y. and Zhang, D.-J. (2003) The Multisoliton Solu-tions of the KP Equation with Self-Consistent Sources. Journal of the Physical Society of Japan, 72, 2184-2192. https://doi.org/10.1143/JPSJ.72.2184
- 8. Hu, X.-B. and Wang, H.-Y. (2006) Construction of dKP and BKP Equations with Self Consistent Sources. Inverse Problems, 22, 1903-1920. https://doi.org/10.1088/0266-5611/22/5/022
- 9. Yao, Y.-Q. and Zeng, Y.-B. (2008) Integrable Rosochatius De-formations of Higher-Order Constrained Flows and the Soliton Hierarchy with Self-Consistent Sources. Journal of Physics A: Mathematical and Theoretical, 41, Article No. 295205. https://doi.org/10.1088/1751-8113/41/29/295205
- 10. Zhu, J.-Y. and Geng, X.-G. (2012) A Hierarchy of Coupled Evolution Equations with Self-Consistent Sources and the Dressing Method. Journal of Physics A: Mathematica and Theoretical, 46, Article No. 035204. https://doi.org/10.1088/1751-8113/46/3/035204
- 11. Wang, H. and Xia, T.-C. (2013) Conservation Laws and Self-Consistent Sources for a Super KN Hierarchy. Applied Mathematics and Computation, 219, 5458-5464. https://doi.org/10.1016/j.amc.2012.11.042
- 12. Ma, W.-X. (2015) Lump Solutions to the Kadomtsev-Petviashvili Equation. Physics Letters A, 379, 1975-1978. https://doi.org/10.1016/j.physleta.2015.06.061
- 13. Yang, J.-Y. and Ma, W.-X. (2017) Abundant Interaction So-lutions of the KP Equation. Nonlinear Dynamics, 89, 1539-1544. https://doi.org/10.1007/s11071-017-3533-y
- 14. Zhao, H.-Q. and Ma, W.-X. (2017) Mixed Lump-Kink Solutions to the KP Equation. Computers & Mathematics with Applications, 74, 1399-1405. https://doi.org/10.1016/j.camwa.2017.06.034
- 15. Yang, J.-Y. and Ma, W.-X. (2016) Lump Solutions of the BKP Equation by Symbolic Computation. International Journal of Modern Physics B, 30, Article No. 1640028. https://doi.org/10.1142/S0217979216400282
- 16. Zhang, J.-B. and Ma, W.-X. (2017) Mixed Lump-Kink Solu-tions to the BKP Equation. Computers & Mathematics with Applications, 74, 591-596. https://doi.org/10.1016/j.camwa.2017.05.010
- 17. Ma, W.-X., Yong, X.-L. and Zhang, H.-Q. (2018) Diversity of Interaction Solutions to the (2+1)-Dimensional Ito Equation. Computers & Mathematics with Applications, 75, 289-295. https://doi.org/10.1016/j.camwa.2017.09.013
- 18. Yong, X.-L., Ma, W.-X., Huang, Y.-H. and Liu, Y. (2018) Lump Solutions to the Kadomtsev-Petviashvili I Equation with a Self-Consistent Source. Computers and Mathematics with Applications, 75, 3414-3419. https://doi.org/10.1016/j.camwa.2018.02.007
- 19. Ablowitz, M.J. and Satsuma, J. (1978) Solitons and Rational Solutions of Nonlinear Evolution Equations. Journal of Mathematical Physics, 19, 2180-2186. https://doi.org/10.1063/1.523550
- 20. Kaup, D.J. (1981) The Lump Solutions and the Backlund Transformation for the Three-Dimensional Three-Wave Resonant Interaction. Journal of Mathematical Physics, 22, 1176-1181. https://doi.org/10.1063/1.525042
- 21. Gilson, C.R. and Nimmo, J.J.C. (1990) Lump Solutions of the BKP Equa-tion. Physics Letters A, 147, 472-476. https://doi.org/10.1016/0375-9601(90)90609-R
- 22. Imai, K. (1997) Dromion and Lump Solutions of the Ishimori-I Equation. Progress of Theoretical Physics, 98, 1013-1023. https://doi.org/10.1143/PTP.98.1013
- 23. Zhang, X. and Chen, Y. (2017) Rogue Wave and a Pair of Resonance Stripe Solitons to a Reduced (3+1)-Dimensional Jimbo—Miwa Equation. Communications in Nonlinear Science and Numerical Simulation, 52, 24-31. https://doi.org/10.1016/j.cnsns.2017.03.021
- 24. Pu, J.-C. and Hu, H.-C. (2018) Mixed Lump—Soliton Solutions of the (3+1)-Dimensional Soliton Equation. Applied Mathematics Letters, 85, 77-81. https://doi.org/10.1016/j.aml.2018.05.017
- 25. Foroutan, M., Manafian, J. and Ranjbaran, A. (2018) Lump Solu-tion and Its Interaction to (3+1)-D Potential-YTSF Equation. Nonlinear Dynamics, 92, 2077-2092. https://doi.org/10.1007/s11071-018-4182-5
- 26. Zhang, Y., Liu, Y.-P. and Tang, X.-Y. (2018) M-Lump and In-teractive Solutions to a (3+1)-Dimensional Nonlinear system. Nonlinear Dynamics, 93, 2533-2541. https://doi.org/10.1007/s11071-018-4340-9
- 27. Zhang, J.-G. and Zhang, Y.-F. (2018) Construction of Lump Soliton and Mixed Lump Stripe Solutions of (3+1)- Dimensional Soliton Equation. Results in Physics, 10, 94-98. https://doi.org/10.1016/j.rinp.2018.05.022
- 28. Ma, W.-X. (2016) Lump-Type Solutions to the (3+1)-Dimensional Jimbo—Miwa Equation. International Journal of Nonlinear Sciences and Numerical Simulation, 17, 355-359. https://doi.org/10.1515/ijnsns-2015-0050
- 29. Yang, J.-Y. and Ma, W.-X. (2017) Abundant Lump-Type Solutions of the Jimbo—Miwa Equation in (3+1)-Dimensions. Computers and Mathematics with Applications, 73, 220-225. https://doi.org/10.1016/j.camwa.2016.11.007
- 30. Batwa, S. and Ma, W.-X. (2018) A Study of Lump-Type and Interaction Solutions to a (3+1)-Dimensional Jimbo—Miwa-Like Equation. Computers and Mathematics with Applications, 76, 1576-1582. https://doi.org/10.1016/j.camwa.2018.07.008
- 31. Wang, H.-Y. and Wen, D.-H. (2012) A (3+1)-Dimensional KP Equation with Self-Consistent Source. Journal of Zhengzhou University, 44, 6-10.
- 32. Hirota, R. (2004) The Direct Method in Soliton Theory. Cambridge University Press, New York. https://doi.org/10.1017/CBO9780511543043
NOTES
*通讯作者。