ABSTRACT

Based on the problem of tensor nuclear norm, a new robust principal component analysis model is established by substituting truncated nuclear norm for nuclear norm, and the convex optimization problem is solved by augmented Lagrange multiplier method. In the experiment of image denoising, the robust principal component analysis model with truncated unclear norm has good denosing effect.

Keywords:Truncated Nuclear Norm, Augmented Lagrange Multipliers, Tensor Singular Value Decomposition, Image Denoising

基于截断核范数的张量去噪

冯晓亭，马婷婷

辽宁师范大学数学学院，辽宁 大连

收稿日期：2019年9月24日；录用日期：2019年10月4日；发布日期：2019年10月11日

摘 要

基于张量核范数问题，用截断核范数代替核范数，建立一个新的截断核范数鲁棒主成分分析(Truncated Nuclear Norm Robust Principal Component Analysis, TNNRPCA)模型，并使用增广拉格朗日乘子法对这个凸优化问题求解。在图像去噪的实验过程中，截断核范数的鲁棒主成分分析模型去噪效果好。

关键词 :截断核范数，增广拉格朗日乘子法，张量奇异值分解，图像去噪

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随着稀疏与低秩知识的深入，主成分分析模型 [1] 对于低秩矩阵恢复潜力巨大，但由于主成分分析模型中的特征值分解有一些局限性，并且在非高斯分布情况下，主成分分析模型得出结果可能并不是最优的。Candès等 [2] 将主成分分析推广到了鲁棒主成分分析(Robust Principal Component Analysis, RPCA) [3] 模型。

由于矩阵的秩非凸，且函数不连续，RPCA构建的模型为一个NP-Hard的优化问题，不易求解。所以引入核范数鲁棒主成分分析 [4] ，该算法对矩阵中的不同奇异值求和，优化时有相同的惩罚力度。但在不同大小的奇异值中，前 $r$ 个较大的奇异值在核范数中起了主要作用，所以核范数在图像去噪方面效果仍不是特别理想，导致实际问题中求出的模型的次优解。为更精确刻画低秩的部分，Hu [5] 等人提出截断核范数的概念，构建截断核范数优化模型，弥补了核范数的不足，使求解后的张量数据恢复的更好。在现有文献基础上，将矩阵鲁棒主成分分析方法运用于高维数据去噪，这种基于矩阵鲁棒主成分分析模型的方法对于结构简单的高维数据，具有较好的去噪效果。因此我们在张量中的模型是基于张量奇异值分解(Tensor Singular Value Decomposition, t-SVD) [6] 和张量截断核范数的鲁棒主成分分析，它的目的是通过求解一个目标为张量截断核范数与 ${\mathcal{l}}_1$ 范数加权组合的模型，可以精确地恢复一个被稀疏误差损坏的低秩张量。

2. 预备知识

定义1 [7] 张量 $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$ 的核范数记为 ${\Vert \mathcal{A}\Vert }_{\ast }$，表示 $\bar{\mathcal{A}}$ 所有正面切片核范数的平均值，即：

${\Vert \mathcal{A}\Vert }_{\ast }:=\frac{1}{n_3}{\displaystyle {\sum }_{i=1}^{n_3}{\Vert {\bar{A}}^{\left(i\right)}\Vert }_{\ast }}$ (1)

定义2 [8] 张量 $\mathcal{X}\in {ℝ}^{n_1\times n_2\times n_3}$ 的截断核范数记为 ${\Vert \mathcal{X}\Vert }_r$，被定义为：

${\Vert \mathcal{X}\Vert }_r={\Vert \mathcal{X}\Vert }_{\ast }-\underset{\begin{array}{l}\mathcal{A}\ast {\mathcal{A}}^{\text{T}}=\mathcal{I}\\ \mathcal{B}\ast {\mathcal{B}}^{\text{T}}=\mathcal{I}\end{array}}{\max }tr\left(\mathcal{A}\ast \mathcal{X}\ast \mathcal{B}\right)$ (2)

其中 $\mathcal{A}\in {ℝ}^{n_1\times r\times n_3}$， $\mathcal{B}\in {ℝ}^{n_2\times r\times n_3}$ 是由t-SVD生成的，其中 $\mathcal{A}$ 和 $\mathcal{B}$ 分别为t-SVD中的 $\mathcal{U}$ 和 $\mathcal{V}$ 在第二维度中的前r列。

定义3 [7] 已知 ${\mathcal{A}}_0\in {ℝ}^{n_1\times n_2\times n_3}$ 可以进行t-SVD，要使得 ${\mathcal{A}}_0$ 满足带有参数 $\mu$ 的张量非相干条件，则需满足：

$\underset{i=1,\cdots ,n_1}{\max }{\Vert {\mathcal{U}}^{\ast }\ast \stackrel{\circ }{{\mathfrak{e}}_i}\Vert }_F\le \sqrt{\frac{\mu r}{n_1{n}_3}}$ (3)

$\underset{j=1,\cdots ,n_2}{\max }{\Vert {\mathcal{V}}^{\ast }\ast \stackrel{\circ }{{\mathfrak{e}}_j}\Vert }_F\le \sqrt{\frac{\mu r}{n_2{n}_3}}$ (4)

和

${\Vert \mathcal{U}\ast {\mathcal{V}}^{\ast }\Vert }_{\infty }\le \sqrt{\frac{\mu r}{n_1{n}_2{n}_2^3}}$ (5)

定理1 [1] 设 $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$ 的t-SVD为：

$\mathcal{A}=\mathcal{U}\ast \mathcal{S}\ast {\mathcal{V}}^{\ast }$ (6)

$\mathcal{U}\in {ℝ}^{n_1\times n_1\times n_3},\mathcal{V}\in {ℝ}^{n_2\times n_2\times n_3}$ 是正交的， $\mathcal{S}\in {ℝ}^{n_1\times n_2\times n_3}$ 是f-对角张量。

引理1 [8] 已知张量 $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$ 的t-SVD为 $\mathcal{U}\ast \mathcal{S}\ast {\mathcal{V}}^{\ast }$，奇异阈值算子定义为：

(7)

3. 截断核范数的鲁棒主成分分析

3.1. 模型的建立

已知一个数据张量 $\mathcal{X}\in {ℝ}^{n_1\times n_2\times n_3}$，假设张量可以通过t-SVD分解成低秩分量 ${\mathcal{L}}_0\in {ℝ}^{n_1\times n_2\times n_3}$ 和稀疏分量 ${\mathcal{E}}_0\in {ℝ}^{n_1\times n_2\times n_3}$，核范数鲁棒主成分分析模型如下式所示：

(8)

其中 $\lambda =1/\sqrt{\max \left(n_1,n_2\right)n_3}$。

式(8)中， ${\Vert \mathcal{L}\Vert }_{\ast }$ 为张量 $\mathcal{L}$ 的核范数，根据张量的奇异值分解，在核范数最小化问题中，所有的奇异值同时被最小化，这样不能对原始张量进行很好地秩估计。为了保证数据不被过多丢失，增强模型鲁棒性，用截断式核范数代替核范数，构建了基于张量截断核范数与 ${\mathcal{l}}_1$ 范数的鲁棒主成分分析模型，如式(9)所示：

(9)

3.2. 模型的求解

根据定义2且引入辅助变量 $\mathcal{W}\in {ℝ}^{n_1\times n_2\times n_3}$，得到优化问题(9)的如下形式：

$\underset{X}{\min }{\Vert X\Vert }_{\ast }-Tr\left({\mathcal{A}}_l\mathcal{W}{\mathcal{B}}_l^{\text{T}}\right)+\lambda {\Vert \mathcal{E}\Vert }_1\text{s}\text{.t}\text{.}\mathcal{L}=\mathcal{W},\mathcal{X}=\mathcal{L}+\mathcal{E}$ (10)

对式(10)构建增广拉格朗日函数：

$\begin{array}{c}L\left(\mathcal{L},\mathcal{E},\mathcal{W},{\mathcal{Y}}_1,{\mathcal{Y}}_2\right)={\Vert \mathcal{L}\Vert }_{\ast }-Tr\left({\mathcal{A}}_l\mathcal{W}{\mathcal{B}}_l^{\text{T}}\right)+\lambda {\Vert \mathcal{E}\Vert }_1+\langle {\mathcal{Y}}_1,\mathcal{L}+\mathcal{E}-\mathcal{X}\rangle \\ +\langle {\mathcal{Y}}_2,\mathcal{L}-\mathcal{W}\rangle +\frac{\mu }{2}\left({\Vert \mathcal{L}+\mathcal{E}-\mathcal{X}\Vert }_F^2+{\Vert \mathcal{L}-\mathcal{W}\Vert }_F^2\right)\end{array}$ (11)

其中张量 ${\mathcal{Y}}_1,{\mathcal{Y}}_2$ 为拉格朗日乘子，惩罚系数 $\mu >0$。

使用交替方向法迭代更新张量 $\mathcal{L},\mathcal{E},\mathcal{W},{\mathcal{Y}}_1,{\mathcal{Y}}_2$ 和惩罚系数 $\mu$。求解目标函数的详细流程如下：

固定 ${\mathcal{E}}_k,{\mathcal{W}}_k,{\mathcal{Y}}_{1,k},{\mathcal{Y}}_{2,k}$，更新 ${\mathcal{L}}_{k+1}$ ：

$\begin{array}{c}{\mathcal{L}}_{k+1}=\arg \underset{\mathcal{L}}{\min }{\Vert \mathcal{L}\Vert }_{\ast }+\langle {\mathcal{Y}}_{1,k},\mathcal{L}+{\mathcal{E}}_k-\mathcal{X}\rangle +\langle {\mathcal{Y}}_{2,k},\mathcal{L}-{\mathcal{W}}_k\rangle +\frac{\mu }{2}\left({\Vert \mathcal{L}+{\mathcal{E}}_k-\mathcal{X}\Vert }_F^2+{\Vert \mathcal{L}-{\mathcal{W}}_k\Vert }_F^2\right)\\ =\arg \underset{\mathcal{L}}{\min }{\Vert \mathcal{L}\Vert }_{\ast }+\mu {\Vert \mathcal{L}+\frac{1}{2}\left({\mathcal{E}}_k-\mathcal{X}-{\mathcal{W}}_k+\frac{1}{\mu }\left({\mathcal{Y}}_{1k}+{\mathcal{Y}}_{2k}\right)\right)\Vert }_F^2\end{array}$ (12)

根据引理1，(12)式可以化简为：

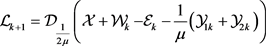(13)

固定 ${\mathcal{L}}_{k+1},{\mathcal{W}}_k,{\mathcal{Y}}_{1,k},{\mathcal{Y}}_{2,k}$，更新 ${\mathcal{E}}_{k+1}$ ：

$\begin{array}{c}{\mathcal{E}}_{k+1}=\arg \underset{\mathcal{E}}{\min }\lambda {\Vert \mathcal{E}\Vert }_1+\langle {\mathcal{Y}}_{1k},{\mathcal{L}}_{k+1}+\mathcal{E}-\mathcal{X}\rangle +\frac{\mu }{2}{\Vert {\mathcal{L}}_{k+1}+\mathcal{E}-\mathcal{X}\Vert }_F^2\\ =\arg \underset{\mathcal{E}}{\min }\lambda {\Vert \mathcal{E}\Vert }_1+\frac{\mu }{2}{\Vert \mathcal{E}+\left({\mathcal{L}}_{k+1}-\mathcal{X}+\frac{1}{\mu }{\mathcal{Y}}_{1,k}\right)\Vert }_F^2\end{array}$ (14)

通过软阈值收缩算子，可以转化为：

${\mathcal{E}}_{k+1}={\mathcal{S}}_{\frac{\lambda }{{\mu }_k}}\left(\mathcal{X}-{\mathcal{L}}_{k+1}-\frac{1}{\mu }{\mathcal{Y}}_{1,k}\right)$ (15)

固定 ${\mathcal{L}}_{k+1},{\mathcal{E}}_{k+1},{\mathcal{Y}}_{1,k},{\mathcal{Y}}_{2,k}$，更新 ${\mathcal{W}}_{k+1}$ ：

${\mathcal{W}}_{k+1}=\arg \underset{\mathcal{W}}{\min }-Tr\left({\mathcal{A}}_l\mathcal{W}{\mathcal{B}}_l^{\text{T}}\right)+\langle {\mathcal{Y}}_{2k},{\mathcal{L}}_{k+1}-\mathcal{W}\rangle +\frac{\mu }{2}{\Vert {\mathcal{L}}_{k+1}-\mathcal{W}\Vert }_F^2$ (16)

(16)式为关于 $\mathcal{W}$ 的二次项，令其导数为0，可得到闭式解。去掉无关项得：

${\mathcal{W}}_{k+1}=\arg \underset{\mathcal{W}}{\min }-Tr\left({\mathcal{A}}_l\mathcal{W}{\mathcal{B}}_l^{\text{T}}\right)+\frac{\mu }{2}{\Vert \mathcal{W}\Vert }_F^2+\langle -{\mathcal{Y}}_{2k},\mathcal{W}\rangle +\mu \langle -{\mathcal{L}}_{k+1},\mathcal{W}\rangle$ (17)

求导：

$-{\mathcal{A}}_l{\mathcal{B}}_l^{\text{T}}+\mu \mathcal{W}-{\mathcal{Y}}_{2k}-\mu {\mathcal{L}}_{k+1}=0$ (18)

$\mathcal{W}={\mathcal{L}}_{k+1}+\frac{1}{\mu }\left({\mathcal{A}}_l{\mathcal{B}}_l^{\text{T}}+{\mathcal{Y}}_{2k}\right)$ (19)

更新 ${\mathcal{Y}}_{1k+1}$， ${\mathcal{Y}}_{2k+1}$ ：

$\begin{array}{l}{\mathcal{Y}}_{1k+1}={\mathcal{Y}}_{1k}+\mu \left({\mathcal{L}}_{k+1}+{\mathcal{E}}_{k+1}-\mathcal{X}\right)\\ {\mathcal{Y}}_{2k+1}={\mathcal{Y}}_{2k}+\mu \left({\mathcal{L}}_{k+1}-{\mathcal{W}}_{k+1}\right)\end{array}$ (20)

4. 实验

实验将本文模型与TRPCA、TNNR、SNN这 3个模型作比较，选取图片大小 $321\times 481\times 3$，椒盐噪声为20%的彩色图片。通过对比彩色图片的恢复情况，得到张量去噪模型的恢复效果。下面列出在单张彩色图片上这四种模型恢复上的效果，如图1所示。同时为了准确评估算法之间恢复的效果，采用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)来衡量四种模型在相同噪声情况下数据的高低，其中PSNR越高，噪声数据恢复的效果越好，数据如表1所示。

图1. 不同方法去噪效果对比

表1. 各算法去噪后的数据

5. 结论

当初始条件相同时，通过图1得出，TRPCA、TNNR、SNN模型恢复出来的彩色图片与原始彩色图片有一定区别。而本文模型对张量数据的恢复更接近于原始彩色图片，即说明使用截断核范数的方法可以有效去除较大奇异值对于噪声产生的不良影响。通过表1数据显示，在相同噪声情况下，本模型PSNR要高于其他模型，同时在迭代次数以及迭代时间上都优于其他模型，实验结果证明本文所建模型的有效性和可行性。总体上来说，TNNRPCA能够比较准确地恢复出彩色图片。

文章引用

冯晓亭,马婷婷. 基于截断核范数的张量去噪
Tensor Denoising Based on Truncated Nuclear Norm[J]. 应用数学进展, 2019, 08(10): 1592-1596. https://doi.org/10.12677/AAM.2019.810186

参考文献