Advances in Applied Mathematics
Vol.
10
No.
10
(
2021
), Article ID:
45545
,
6
pages
10.12677/AAM.2021.1010338
基于分数阶SIR模型的新冠肺炎疾病的 传播预测
任 磊*,米冬茜
商丘师范学院数学与统计学院,河南 商丘
收稿日期:2021年8月26日;录用日期:2021年9月15日;发布日期:2021年9月28日

摘要
本文提出了用于预测新冠肺炎疾病传播的分数阶SIR (susceptible-infected-recovered)模型,基于Caputo分数阶导数的有限差分方法完成了时域模型的实现,然后研究了分数阶导数值对所提出的分数阶SIR模型的动态特性的影响。
关键词
分数阶系统,新冠肺炎,SIR模型

Prediction of Novel Coronavirus Pneumonia Transmission Based on Fractional SIR Model
Lei Ren*, Dongqian Mi
School of Mathematics and Statistics, Shangqiu Normal University, Shangqiu Henan
Received: Aug. 26th, 2021; accepted: Sep. 15th, 2021; published: Sep. 28th, 2021

ABSTRACT
A novel coronavirus pneumonia model is proposed to predict the spread of new crown pneumonia disease. The SIR model (susceptible-infected-recovered) is implemented. The time domain model is implemented by the Caputo finite difference method with fractional derivative. Then the influence of fractional values on the dynamic characteristics of the fractional SIR model is studied.
Keywords:Fractional System, COVID-19, SIR Model

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
冠状病毒病是由SARS-CoV-2病毒感染引起的呼吸系统急性传染病,感染症状通常是发烧、干咳、疲劳、食欲不振和呼吸急促。新冠肺炎于2019年12月8日在中国武汉首次被识别和描述。由于该病毒迅速传播到其他国家和大陆,2020年3月11日,世界卫生组织将新冠肺炎归类为大流行病。从死亡率和传染率来看,新冠肺炎被认为是自20世纪初流感大流行以来现代最严重的流行病。
传染病传播动力学的数学建模理论引起了相当大的研究兴趣,因为新冠肺炎疫情的全球性问题吸引了来自不同领域的研究人员 [1] [2] [3]。Susceptible-Infected-Removed (SIR)流行病模型是一种经典的隔室模型,广泛用于预测传染病的进展 [4] [5] [6]。
尽管SIR模型在模拟多个流行过程中可能有用,但它可能不足以描述新冠肺炎的传播动态。因此,对用于近似新冠肺炎疾病的SIR模型进行了一些修改使用SEIR (易感暴露感染去除)隔室模型来研究新冠肺炎的传播和控制。文献 [7] 提出了一种SEIR模型,通过添加接触者追踪和其他干预措施(例如隔离、锁定和社会疏远)来扩展。Giordano等人 [8] 提出了区分确诊和未确诊个体的SIDARTHE (易感–感染–诊断–患病–识别–威胁–治愈–灭绝)模型。
众所周知,分数阶微积分具有非局部性,更适合描述复杂流体的渗流、弹性体的热传导等具有记忆性和遗传性质的数学模型。在各种物理过程的微分方程中利用分数阶微积分建模可以显着提高多个过程的建模性能。因此,许多科学家开始关注这个数学分支,因为它可以更好地理解一些普通微积分无法提供精确解释的复杂物理现象。Atangana和Gómez-Aguilar [9] 应用分数阶导数来模拟混沌和统计。莫拉莱斯–德尔加多等人 [10] 获得了涉及Caputo-Fabrizio和Atanagana-Baleanu分数导数的癌症化疗效果模型的解决方案。Khan和Atangana [11] 提出并研究了一种考虑人与感染源(海鲜市场)之间相互作用的分数阶扩展SEIR (易感暴露感染去除)模型。
在本文中,我们将Caputo分数阶导数运用到经典SIR模型中,以模拟和预测新冠肺炎的传播。本文的结构如下:在引言中介绍了对新冠肺炎传播的相关建模问题,第1节介绍了经典的SIR模型,第2节介绍了SIR模型的分数阶推广及其固定步长的实现。第3节介绍了分数阶对模型动态特性的影响,并介绍了局部区域的病毒传播模型,第4节的小结概括了本文。
2. 预备知识
SIR模型是最简单的隔室模型之一,许多其他模型是其基本形式的派生形式。SIR模型将总人口N分为三类:易感个体的数量(S),感染者的数量(I),恢复个体的数量(R)。SIR模型通常由三个常微分方程组成,如下所示
(1)
其中 和 分别为感染率和恢复率。
一般的SIR模型中,出生和死亡动态通常被忽略,基于流行病的特点,其传播速度通常比出生和死
亡快得多,并且数值模拟一般也在较短的时间间隔内执行。传染病的动态取决于比率 ,其中 是
基本再生数。该比率量化了受感染人群中一个人直接产生的预期病例数。当 时,感染将能够开始传播,从而导致潜在的爆发。当 ,疾病感染然人群将逐步衰减直至消失。
3. 分数阶SIR模型
通常情况下,常见方程中大多数整数阶导数可以推广到分数阶导数。分数阶导数通常表示为 ,其中阶数 。分数阶导数通常有三个定义,如Caputo分数阶导数、Rieman-Liouville分数阶导数和Grünwald-Letnikov (G-L)分数阶导数。在本文中利用形如下列的Caputo分数阶导数:
(2)
其中 是Caputo分数阶导数的阶。
在时间的离散上,使用 逼近格式,具体逼近格式如下:
(4)
易知,在模型方程中加入分数阶导数可以改善物理过程中的模型参数。特别是,使用分数阶微分方程可以更好地模拟各种传播与扩散过程。考虑到病毒传播是与上述类似的一类过程,分数阶SIR模型可以显著提高某些数学模型的性能。在这种情况下,整数阶差分格式由分数阶导数差分格式代替可得:
(5)
其中 ,。SIR模型动力学的分数阶推广不同于一般情况下的模型推广。分数阶模型的若干性质与整数阶不同,例如总人口数N在分数阶模型下是随时间变化的。因此,分数阶SIR模型应该被认为是一种启发式模型,不直接依赖于物理现象。此外,值得强调的是,在这种情况下,我们有三个额外的估计参数 ,,它们是分数阶导数的不同阶数。
考虑到在大多数地区,新冠肺炎统计数据每周或者每天呈现一次,对于病毒传播的预测,我们可以使用离散时间 差分格式,因此我们有
(6)
结合方程(4)和(6),我们可以得到基于Caputo分数阶导数的分数阶SIR模型:
(7)
为了对新冠肺炎的传播进行数学建模,我们需要给出模型参数 。其中参数N是任意给定的,其余参数在实际模型中要根据具体情况来确定。在下一节中,我们将验证分数阶 , 对模型动力学特性的影响。
4. 数值模拟
本节将介绍所提出的分数阶SIR模型(7)的动态,并展示分数阶差分如何改变数值结果。首先,我们将展示具有不同分数阶数的模拟,以演示它们的值如何影响隔室种群,并给出分数阶SIR模型的动力学特性。
考虑具有以下参数的三组模拟: ,,,,,, 以及 。在每一组中,只有一个 改变,而剩下的两个等于1。这样,我们可以看到特定的分数阶 , 如何影响模型。图1,图2呈现模拟结果。
由于 , 的情况类似,所以我们仅做出分数阶导数 变化的情形作图。从图1,图2中可以看到,分数阶 和 影响整个模型,而 只影响移除的隔室,这一结果和我们的模型方程(7)的预期是一致的。参数越多,所呈现的模型就越复杂,但也更通用。上述结果表明,分数阶SIR模型更契合于现实生活过程的数学模型。
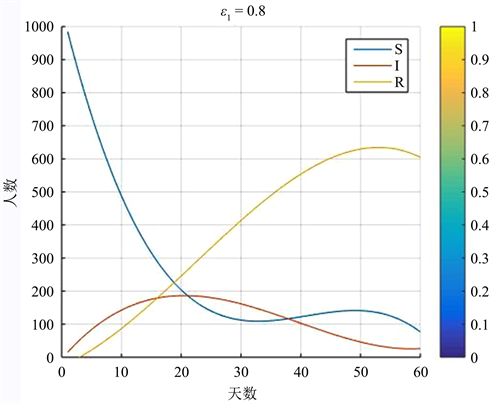
Figure 1. The simulate result of ε1 = 0.8 and ε2 = ε3 = 1
图1. 当ε1 = 0.8时,ε2 = ε3 = 1模拟结果

Figure 2. The simulate result of ε1 = 0.4 and ε2 = ε3 = 1
图2. 当ε1 = 0.4时,ε2 = ε3 = 1模拟结果
5. 小结
本文中给出了分数阶SIR模型,用来预测新冠肺炎疾病的传播。模型的实现基于Caputo分数阶导数及其离散化。我们研究了模型导数的分数阶对所提出模型的动态特性的影响。在对新冠肺炎传输进行建模时,模型的参数是在使用遗传算法的同时进行估计的。该模型具有一些局限性,模型的预测并不代表真实数据。在这种情况下,需要使用分数阶SIR模型或更复杂的流行病模型的时变参数。尽管如此,该研究表明,所提出的模型是有效的,并且可能对未来的流行病研究有用。
基金项目
本研究由河南省高等学校重点科研项目“反常扩散模型的数值分析及其在土壤污染中的应用研究”资助,批准号21A110020。本研究由商丘师范学院新冠肺炎疫情防控应用型科研项目“基于SIR模型对新型冠状病毒肺炎疫情的趋势预测与仿真模拟”资助,批准号SQSYXGYQ2020008。
文章引用
任 磊,米冬茜. 基于分数阶SIR模型的新冠肺炎疾病的传播预测
Prediction of Novel Coronavirus Pneumonia Transmission Based on Fractional SIR Model[J]. 应用数学进展, 2021, 10(10): 3233-3238. https://doi.org/10.12677/AAM.2021.1010338
参考文献
- 1. Hu, Z.L., Song, S., Xu, C.J., et al. (2020) Clinical Characteristics of 24 Asymptomatic Infections with COVID-19 Screened among Close Contacts in Nanjing, China. Science China Life Sciences, 63, 706-719. https://doi.org/10.1007/s11427-020-1661-4
- 2. Guo, Y.-R., Cao, Q.-D., Hong, Z.-S., et al. (2020) The Origin, Transmission and Clinical Therapies on Coronavirus Disease 2019 (COVID-19) Outbreak—An Update on the Status. Military Medical Research, 7, 93-103. https://doi.org/10.1186/s40779-020-00240-0
- 3. 曹盛力, 冯沛华, 时朋朋. 修正SEIR传染病动力学模型应用于湖北省2019冠状病毒病(COVID-19)疫情预测和评估[J]. 浙江大学学报(医学版), 2020, 49(2): 178-184.
- 4. 李东辉, 郑三强, 杨淑伶. K-means聚类算法在SIR传染病模型中的应用研究[J]. 数学的实践与认识, 2021, 51(2): 268-276.
- 5. 庞金彪, 鹿利. SIR型传染病模糊控制模型及其应用[J]. 中国卫生统计, 2003, 20(3): 154-157.
- 6. 张艳霞, 李进. 基于SIR模型的新冠肺炎疫情传播预测分析[J]. 安徽工业大学学报(自然科学版), 2020, 37(1): 94-101.
- 7. 范如国, 王奕博, 罗明, 张应青, 朱超平. 基于SEIR的新冠肺炎传播模型及拐点预测分析[J]. 电子科技大学学报, 2020, 49(3): 369-374.
- 8. Giordano, G., Blanchini, F., Bruno, R., Colaneri, P., Filippo, A.D., Matteo, A.D. and Colaneri, M. (2020) Modelling the COVID-19 Epidemic and Implementation of Population-Wide Interventions in Italy. Nature Medicine, 26, 855-860. https://doi.org/10.1038/s41591-020-0883-7
- 9. Atangana, A. and Gómez-Aguilar, J. (2018) Fractional Derivatives with No-Index Law Property: Application to Chaos and Statistics. Chaos Solitons Fractals, 114, 516-535. https://doi.org/10.1016/j.chaos.2018.07.033
- 10. Morales-Delgado, V.F., Gómez-Aguilar, J.F., Saad, K. and Jiménez, R.F.E. (2019) Application of the Caputo-Fabrizio and Atangana-Baleanu Fractional Derivatives to Mathematical Model of Cancer Chemotherapy Effect. Mathematical Methods in the Applied Sciences, 42, 1167-1193. https://doi.org/10.1002/mma.5421
- 11. Khan, M.A. and Atangana, A. (2020) Modeling the Dynamics of Novel Coronavirus (2019-nCov) with Fractional Derivative. Alexandria Engineering Journal, 59, 2379-2389. https://doi.org/10.1016/j.aej.2020.02.033
NOTES
*第一作者。