上海理工大学，管理学院，上海

收稿日期：2022年12月1日；录用日期：2022年12月29日；发布日期：2023年1月6日

摘要

面对被严重稀疏噪声损坏的观测数据，采用L₁范数来度量稀疏性的低秩恢复算法已不能很好的从退化的观测矩阵中恢复低秩结构。本文提出了一个新的加权低秩矩阵恢复算法用于图像去噪。利用L_1/2范数来度量稀疏性，引入权重分配给每个组成元素，并结合L_p范数特定情况下(p = 1/2)的封闭阈值算子，提出加权的L_1/2正则化，相比常用的L₁范数更加有效。同时将TV正则化整合到我们的方法中，有效的保证了图像的边缘特征。所提的方法与现有的低秩恢复算法相比，在增强图像结构平滑性和去除大的稀疏噪声方面表现更好，图像重建的质量有了明显提高。

关键词

低秩矩阵恢复，结构平滑性，TV范数

Weighted L_1/2 Norm with TV Regularization for Image Denoising

Wanhong Wu, Zikai Wu^*

Business School, University of Shanghai for Science and Technology, Shanghai

Received: Dec. 1^st, 2022; accepted: Dec. 29^th, 2022; published: Jan. 6^th, 2023

ABSTRACT

In the face of the observation data damaged by serious sparse noise, the low-rank restoration algorithm using L₁ norm to measure sparsity can not better recover the low-rank structure from the degraded observation matrix. In this work, a new weighted low-rank matrix restoration algorithm is proposed for image denoising. The L_1/2 norm is used to measure sparsity, and the weight is assigned to each component element. Combined with the closed threshold operator of L_p norm (p = 1/2), the weighted L_1/2 regularization is proposed, which is more effective than the common L_1/2 norm. At the same time, TV regularization is integrated into our method to effectively ensure the edge features of the image. Compared with the existing low-rank restoration algorithm, the proposed method has better performance in enhancing the smoothness of image structure and removing large sparse noise, and the quality of image reconstruction has been significantly improved.

Keywords:Low-Rank Matrix Recovery, Structure Smoothness, TV Regularization

Copyright © 2023 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随着低秩和稀疏矩阵分析理论的初步建立和不断完善，它逐渐成为在图像信号处理方面的有效工具，并在计算机视觉和模式识别中的有着广泛应用，如图像去噪 [1] [2]，目标追踪 [3] [4]，空间聚类 [5] [6]，推荐系统 [7] 等，该分析理论的目的主要是从退化的观测数据中恢复具有低秩结构的干净数据。

在自然图像中，其数据矩阵通常是低秩或近似低秩的，但存在随机且任意大的误差破坏了这种低秩特性，这类误差分布具有稀疏性。为了从损坏数据中准确恢复出低秩结构，我们可以针对这类破坏数据结构的稀疏误差进行建模。Candès等人 [8] 根据数据的低秩和稀疏特性提出了鲁棒主成分分析(robustprincipal component analysis, RPCA)，通过引入重构误差，加入稀疏约束并最小化低秩数据矩阵的秩，将数据分离成低秩数据和稀疏噪声两部分。由于RPCA是一个NP-hard问题，通常转化为凸优化问题求解，将秩函数最小化近似为核范数最小化(nuclearnormminimization, NNM)，将 ${\mathcal{l}}_0$ 范数最小化近似为 ${\mathcal{l}}_1$ 范数最小化来处理，但是这种简单的凸近似很容易引起解的过收缩问题，容易导致数据信息过多地丢失而影响图像重建的质量。Gu等人 [9] 为了增强低秩解的准确性，提出了加权核范数最小化(weight NNM, WNNM)对不同大小的奇异值分量采用相应的惩罚权重，能更灵活地处理实际问题。受到加权 ${\mathcal{l}}_1$ 范数最小化能增强稀疏性的启发，Peng等人 [10] 提出了对低秩和稀疏成分双重加权的恢复算法，并在迭代过程中重新分配权重，大大提高了低秩矩阵的性能恢复。然而这类方法在处理内在秩较高的或者被高密度噪声损坏的数据时，仍然存在显著的性能退化，且他们均未考虑图像的结构平滑性。

本文提出了一个双重加权的低秩恢复算法，采用加权核范数来增强低秩性，并提出了一个改进的稀疏正则项，即加权 ${\mathcal{l}}_{1/2}$ 范数最小化。 ${\mathcal{l}}_{1/2}$ 范数相比 ${\mathcal{l}}_1$ 范数在图像恢复方面更有竞争力，因为加权的 ${\mathcal{l}}_{1/2}$ 能够更好的体现观测数据的稀疏性，在处理高密度的稀疏噪声时比 ${\mathcal{l}}_1$ 范数有更好的表现。总变分正则化已被证实在图像处理中是提高图像平滑度的有效工具 [11] [12]，为保持图像的边缘特征和结构平滑性，我们将总变分正则化整合到低秩稀疏模型中提出了基于加权 ${\mathcal{l}}_{1/2}$ 范数和总变分(total variation, TV)正则化的图像去噪算法。该模型整体是一个非凸优化问题，我们采用非精确的拉格朗日算法(inexact augmented lagrange method, IALM)并用交替方向乘子法(alternate direction multiplier method, ADMM)将难以处理的问题分成三个容易处理的子问题进行求解。实验证明，所提的算法明显改善了图像恢复的质量。

2. 相关工作

2.1. 鲁棒主成分分析

Candès等人 [8] 建立了低秩矩阵恢复的有关理论，该理论表明当一个低秩或近似低秩的矩阵的部分元素被破坏后，能通过数学模型方法从损坏的矩阵中恢复出低秩矩阵。RPCA旨在被噪声矩阵S破坏的观测矩阵D中恢复出低秩矩阵L，这里假设矩阵S是稀疏的，具体可以描述为如下的优化问题

$\underset{L,S}{\min }rank\left(L\right)+\lambda {\Vert S\Vert }_{{\mathcal{l}}_0}\text{s}\text{.t}\text{.}D=L+S$ (1)

其中， $rank\left(L\right)$ 为矩阵的秩， ${\Vert S\Vert }_{{\mathcal{l}}_0}$ 表示矩阵中非零元的个数。但是在实际应用中，(1)是一个NP问题，不能直接求解，一个常用的方法就是采用秩函数和 ${\mathcal{l}}_0$ 范数的凸包近似，该方法称为主成分追踪(principal component pursuit, PCP)，即

$\underset{L,S}{\min }{\Vert L\Vert }_{\ast }+\lambda {\Vert S\Vert }_{{\mathcal{l}}_1}\text{s}\text{.t}\text{.}D=L+S$ (2)

其中 ${\Vert L\Vert }_{\ast }={\displaystyle \sum {\sigma }_j\left(L\right)}$，表示矩阵的奇异值之和， ${\Vert S\Vert }_{{\mathcal{l}}_1}={\displaystyle \sum {\left|S\right|}_{i,j}}$，表示所有元素的绝对值之和。该问题的两个子问题可以分别使用奇异值阈值算子和软阈值算子求解 [13]。

2.2. 加权核范数最小化

加权核范数最小化可以用于增强矩阵的低秩结构，假设 $X\in {ℝ}^{m\times n}$，$Y\in {ℝ}^{m\times n}$ 且矩阵的秩为r， $W_X=\left\{w_{X,j}\right\}\in {ℝ}^r$，则加权核范数最小化问题如下

$\underset{X}{\min }\alpha {\displaystyle \underset{j=1}{\overset{r}{\sum }}{w}_{X,j}}\cdot {\sigma }_j+\frac{1}{2}{\Vert X-Y\Vert }_F^2$ (3)

Y的奇异值分解为 $Y=U\Sigma V^{\text{T}}$，$\Sigma =diag\left({\left\{{\sigma }_j\right\}}_{1\le j\le r}\right)$。Peng在 [10] 中提出非均匀阈值(non-uniform singular

value thresholding, NSVT)算子来求解该最小化问题， ${\mathcal{D}}_w\left[Y\right]=U{\mathcal{S}}_w\left[\Sigma \right]V^{\text{T}}$，其中 ${\mathcal{S}}_w\left[\Sigma \right]=diag\left({\left\{{\sigma }_j-w_j\right\}}_{+}\right)$。因此优化问题(2)的最优解为 $X^{*}={\mathcal{D}}_{\alpha w_x}\left[Y\right]$。

2.3. 加权 ${\mathcal{l}}_{1/2}$ 范数最小化

为了增强稀疏解的准确性，我们提出了用于加权 ${\mathcal{l}}_{1/2}$ 范数最小化求解的非均匀半阈值算子，假设 $X\in {ℝ}^{m\times n}$，$Y\in {ℝ}^{m\times n}$，$W=\left\{w_{ij}\right\}\in {ℝ}^{m\times n}$，则加权核范数最小化问题如下

$\underset{X}{\min }{\Vert X-Y\Vert }_F^2+\alpha {\Vert W\odot X\Vert }_{{\mathcal{l}}_{1/2}}^{1/2}$ (4)

该问题的求解受到文献 [14] [15] 的启发，定义非均匀半阈值算子可表示为

${\Gamma }_{\eta }\left(y_{ij}\right)=\{\begin{array}{ll}\frac{2}{3}{y}_{ij}\left[1+\cos \left(\frac{2\pi -2{\psi }_{\eta }\left(y_{ij}\right)}{3}\right)\right],\hfill & \left|y_{ij}\right|>\frac{\sqrt[3]{54{\eta }^2}}{4}\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$ (5)

其中 $\eta =\alpha w_{ij}$，${\psi }_{\eta }\left(y_{ij}\right)=\arccos \left(\frac{\eta }{8}{\left(\left|y_{ij}\right|/3\right)}^{-3/2}\right)$。则优化问题(4)的最优解为 $X^{*}={\Gamma }_{\alpha w}\left(Y\right)$。

2.4. 总变分范数优化模型

Beck和Teboulle [16] 表明在图像处理中TV范数在保留图像的边缘特征和增强图像的结构平滑性起到重要的作用，有关各项同性TV范数的定义如下。

${\Vert X\Vert }_{TV}={\displaystyle \underset{i=1}{\overset{m-1}{\sum }}{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\sqrt{{\left(x_{i,j}-x_{i+1,j}\right)}^2+{\left(x_{i,j}-x_{i,j+1}\right)}^2}}}+{\displaystyle \underset{i=1}{\overset{m-1}{\sum }}\left|x_{i,n}-x_{i+1,n}\right|}+{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\left|x_{m,j}-x_{m,j+1}\right|}$ (6)

使用TV范数最小化的图像去噪问题定义如下

$\begin{array}{l}\underset{X}{\min }\beta {\Vert X\Vert }_{TV}+\frac{1}{2}{\Vert X-C\Vert }_F^2\\ \text{s}\text{.t}.X\in B_{l,u}\equiv \left\{x_{i,j},l\le x_{i,j}\le u\right\}\end{array}$ (7)

其中C是带噪声图像， $\beta$ 是正则项的罚参数 $B_{l,u}$ 是一个集合用于约束图像中的像素值， $\left[l,u\right]=\left[0,255\right]$。对于该问题我们引用了 [16] 中提出的快速梯度投影算法，优化问题的最优解为 $X^{*}=P_{B_{l,u}}\left(C-\beta \mathcal{L}\left(a,b\right)\right)$，其中P是线性算子， $\mathcal{L}$ 是正交投影算子。

3. 低秩恢复模型

本章我们提出了一个双加权的低秩恢复模型，并给证明了其求解过程。

3.1. 模型

为了增强稀疏性，我们提出了加权的 ${\mathcal{l}}_{1/2}$ 范数最小化，在图像去噪中能够更准确的描述稀疏噪声并将其从损坏的数据中去除，同时将TV范数引入目标函数能够保留图像的边缘结构，增强图像的平滑性。为此建立了如下模型

$\begin{array}{l}\underset{L,S}{\min }{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{L,j}}\cdot {\tilde{\sigma }}_j+\lambda {\Vert W_S\odot S\Vert }_{{\mathcal{l}}_{1/2}}^{1/2}+\beta {\Vert L\Vert }_{TV}\\ \text{s}\text{.t}\text{.}D=L+S\\ L\in B_{l,u}\equiv \left\{x_{i,j},l\le x_{i,j}\le u\right\}\end{array}$ (8)

3.2. 模型求解

为了求解(8)中的优化问题，引入辅助变量H，

$\begin{array}{l}\underset{H,L,S}{\min }{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{H,j}\cdot {\sigma }_j}+\lambda {\Vert W_S\odot S\Vert }_{{\mathcal{l}}_{1/2}}^{1/2}+\beta {\Vert L\Vert }_{TV}\\ \text{s}\text{.t}\text{.}H=L,D=L+S\\ L\in B_{l,u}\equiv \left\{x_{i,j},l\le x_{i,j}\le u\right\}\end{array}$ (9)

这里 $W_H=\left\{w_{H,j},j=1,\cdots ,n\right\}$ 为 $\left\{{\sigma }_j\right\}$ 的权重， $\left\{{\sigma }_j\right\}$ 是矩阵H的奇异值。 $W_S$ 为稀疏矩阵S的权重。

因此模型(9)的增广拉格朗日函数为

$\begin{array}{l}\mathcal{L}\left(H,L,S,Y_1,Y_2\right)\\ ={\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{H,j}\cdot {\sigma }_j}+{\Vert W_S\odot S\Vert }_{{\mathcal{l}}_{1/2}}^{1/2}+\beta {\Vert L\Vert }_{TV}+\langle Y_1,D-H-S\rangle +\langle Y_2,L-H\rangle \\ +\frac{\mu }{2}\left({\Vert D-H-S\Vert }_F^2+{\Vert L-H\Vert }_F^2\right)\\ \text{s}\text{.t}\text{.}L\in B_{l,u}\equiv \left\{x_{i,j},l\le x_{i,j}\le u\right\}\end{array}$ (10)

式中， $\langle \cdot ,\cdot \rangle$ 表示两个矩阵的内积， $\mu$ 是拉格朗日惩罚参数。采用ADMM求解一个变量时固定其他变量均保持不变，具体方法如下。

求解H时，固定其他变量均保持不变，

$\begin{array}{l}\arg \underset{H}{\min }{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{H,j}\cdot {\sigma }_j}+\langle Y_1,D-H-S\rangle +\langle Y_2,L-H\rangle +\frac{\mu }{2}\left({\Vert D-H-S\Vert }_F^2+{\Vert L-H\Vert }_F^2\right)\\ =\arg \underset{H}{\min }{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{H,j}\cdot {\sigma }_j}+\mu {\Vert H-\frac{1}{2}\left(D+L-S+Y_1/\mu +Y_2/\mu \right)\Vert }_F^2\\ =\arg \underset{H}{\min }{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{H,j}\cdot {\sigma }_j}+\mu {\Vert H-C\Vert }_F^2\end{array}$ (11)

此处 $C=\frac{1}{2}\left(D+L-S+Y_1/\mu +Y_2/\mu \right)$，时，这个最小化问题可以利用NSVT求解， $H^{*}={\mathcal{D}}_{{\left(2\mu \right)}^{-1}{w}_x}\left[C\right]$。

求解S时，固定其他变量均保持不变，

$\begin{array}{l}\arg \underset{S}{\min }\lambda {\Vert W_S\odot S\Vert }_{{\mathcal{l}}_{1/2}}^{1/2}+\langle Y_1,D-H-S\rangle +\frac{\mu }{2}{\Vert D-H-S\Vert }_F^2\\ =\arg \underset{S}{\min }\lambda {\Vert W_S\odot S\Vert }_{{\mathcal{l}}_{1/2}}^{1/2}+\frac{\mu }{2}{\Vert S-\left(D-H+Y_1/\mu \right)\Vert }_F^2\\ =\arg \underset{S}{\min }\lambda {\Vert W_S\odot S\Vert }_{{\mathcal{l}}_{1/2}}^{1/2}+\mu {\Vert S-K\Vert }_F^2\end{array}$ (12)

其中 $K=D-H+Y_1/\mu$，我们可以通过非均匀半阈值算子求解， $S^{*}={\Gamma }_{2\lambda w_s/\mu }\left(K\right)$。

求解L时，固定其他变量均保持不变，

$\begin{array}{l}\arg \underset{L}{\min }\beta {\Vert L\Vert }_{TV}+\langle Y_2,L-H\rangle +\frac{\mu }{2}{\Vert L-H\Vert }_F^2\\ =\arg \underset{L}{\min }\beta {\Vert L\Vert }_{TV}+\frac{\mu }{2}{\Vert L-\left(H-Y_2/\mu \right)\Vert }_F^2\\ =\arg \underset{L}{\min }\beta {\Vert L\Vert }_{TV}+\frac{\mu }{2}{\Vert L-G\Vert }_F^2\end{array}$ (13)

此处 $G=H-Y_2/\mu$，$L\in B_{l,u}\equiv \left\{x_{i,j},l\le x_{i,j}\le u\right\}$。为求解TV最小化问题采用快速梯度投影算法 [14]， $L^{*}=P_{B_{l,u}}\left(G-\left(\beta /\mu \right)\mathcal{L}\left(a,b\right)\right)$。

3.3. 算法总结

求解加权 ${\mathcal{l}}_{2/3}$ 范数和TV范数的增广拉格朗日算法如算法1，低秩矩阵恢复的图像去噪算法如算法2。

算法1增广拉格朗日算法

输入矩阵 $D\in {ℝ}^{m\times n}$，$\lambda$，$\beta$，$\delta$

初始化： $L_0\in {ℝ}^{m\times n}$，$H_0\in {ℝ}^{m\times n}$，$S_0\in {ℝ}^{m\times n}$，$Y_{1,0}\in {ℝ}^{m\times n}$，$Y_{2,0}\in {ℝ}^{m\times n}$，${\mu }_0>0$，$\xi ={10}^{-7}$，$t=0$，$innertier=100$

1) while ${\Vert D-H-S\Vert }_F/{\Vert D\Vert }_F>\xi$ && $t<innertier$

2) update $H_{t+1}={\mathcal{D}}_{{\left(2{\mu }_t\right)}^{-1}{w}_x}\left[C_{t+1}\right]$

3) update $S_{t+1}={\Gamma }_{2\lambda w_s/{\mu }_t}\left(K_{t+1}\right)$

4) update $L_{t+1}=P_{B_{l,u}}\left(G_{t+1}-\left(\beta /\mu \right)\mathcal{L}\left(a,b\right)\right)$

5) update $Y_{1,t+1}=Y_{1,t}+{\mu }_t\left(D-H_{t+1}-S_{t+1}\right)$

6) update $Y_{2,t+1}=Y_{2,t}+{\mu }_t\left(L_{t+1}-H_{t+1}\right)$

7) update ${\mu }_{t+1}=\delta {\mu }_t$，$t\leftarrow t+1$

8) endwhile

输出： $L_t$，$S_t$

算法2加权 ${\mathcal{l}}_{2/3}$ 范数和TV范数低秩矩阵恢复的图像去噪算法

输入矩阵 $D\in {ℝ}^{m\times n}$，$m\ge n$

初始化： $W_X=\left\{w_{X,j}\right\}\in {ℝ}^n$，$W_S=\left\{w_{S,ij}\right\}\in {ℝ}^{m\times n}$，$\epsilon ={10}^{-7}$

利用PCP [1] 计算出 $L^{\left(0\right)}=U\Sigma V^{\text{T}}$ 和 $S^{\left(0\right)}$，设置权重 $w_{X,j}=\frac{1}{diag{\left(\Sigma \right)}_j+{ϵ}_1}$，$w_{S,ij}=\frac{1}{\left|s_{i,j}\right|+{ϵ}_2}$

1) while ${\Vert D-L-S\Vert }_F/{\Vert D\Vert }_F>\epsilon$

2) 将 $w_{X,j}$ 和 $w_{S,ij}$ 带入算法2中，计算 $L_t$，$S_t$

3) end while

4) 输出 $L^{*}$，$S^{*}$

4. 实验与结果分析

4.1. 实验设置

在实验中，我们设置的参数如下。输入的数据矩阵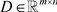，设置初始值 $L_0=0$，$S_0=0$，$H_0=0$，$Y_{1，0}=D/\max \left(\Vert D\Vert ,{\lambda }^{-1}{\Vert D\Vert }_{\infty }\right)$，$Y_{2，0}=0$，$\delta =1.5$，${ϵ}_1={ϵ}_2=0.01$。

在本工作中， $\lambda$ 和 $\beta$ 是用于平衡三个正则项的参数，按照以往的经验 $\lambda$ 取值为 $1/\sqrt{\max \left(m,n\right)}$。而 $\beta$ 的取值控制着TV项的重要程度，因此如何确定 $\beta$ 的取值是一个关键的问题。

当 $\lambda$ 固定时，令 $\beta =2^a\theta$，其中 $\theta =0.00125/\sqrt{\max \left(m,n\right)}$，$a=0,1,\cdots ,8$。分析a取不同值参数 $\beta$ 的变化对图像恢复的影响，选取Lena，Babara，Mountain，Boat四张自然图像用于测试，从图1可以看出 $a=3$ 时图像重建的峰值信噪比更高。所有算法的实验环境为CPUi5-12400，内存16 GB，Windows 10操作系统以及MATLAB 2016a。

图1. 参数β对结果的影响

4.2. 自然图像去噪

为了验证本文提出的基于加权 ${\mathcal{l}}_{1/2}$ 范数和TV正则化的图像去噪算法的有效性与正确性，实验部分将与目前的比较先进的低秩恢复算法做比较，例如PCP [5]，Reweighted l₁ [17]，NSVT [7] 以及SRLRMR [18]，且对应算法的参数均使用他们文中的默认参数。为了客观评价几种方法，采用峰值信噪比(PSNR)和结构相似度(SSIM) [19] 作为评价指标。

选择测试的自然图像如图2所示，从左到右分别标号为1~9。其中我们选择图片5 (Bridge)和图片1 (Lena)加入20%和30%的密度稀疏噪声作为去噪效果展示，如图3和图4。所提的算法显著提高了图像恢复质量，增强了图像结构平滑度。

图2. 用于测试的自然图像

图3. 图像Bridge添加20%稀疏噪声后各算法的去噪结果

图4. 图像Lena添加30%稀疏噪声后各算法的去噪结果

实验测试图像密度为20%，30%，40%声损坏，各种算法的去噪结果总结在表1和表2。从评价指标可以看出所提的算法不论是PSNR还是SSIM的表现都是更加优越的。20%密度的噪声下PSNR和SSIM分别平均约提高2.74 dB，0.018，30%密度的噪声下，PSNR和SSIM分别平均约提高了1.16 dB，0.01。

表1. 各个算法去噪后的PSNR比较

表2. 各个算法去噪后的SSIM比较

5. 结论

本文提出了加权 ${\mathcal{l}}_{1/2}$ 范数最小化，并结合加权核范数和TV正则化建立了一个双加权的低秩恢复模型，利用IALM和ADMM可以有效的处理所提的非凸优化模型。从实验结果可以看出，本文提出的算法在去噪方面效果更优，不仅提高了去噪后图像的结构平滑性，同时保留了较好的边缘特征，重建质量更接近原始图像，图像去噪效果相比PCP，Reweightedl₁，NSVT以及SRLRMA有着明显提升。从而也印证了加权 ${\mathcal{l}}_{1/2}$ 范数相比比加权 ${\mathcal{l}}_1$ 范数，前者能够更好的针对稀疏误差建模。

然而，我们的方法也存在一些未解决的问题，例如如何根据不同水平的噪声自适应的选择参数，以及用理论分析证明算法的收敛性都将是未来值得去研究的问题。

文章引用

吴万红,吴自凯. 基于加权L1/2范数和TV正则化的图像去噪方法
Weighted L1/2 Norm with TV Regularization for Image Denoising[J]. 应用数学进展, 2023, 12(01): 6-14. https://doi.org/10.12677/AAM.2023.121002

参考文献