Statistics and Application
Vol.
13
No.
02
(
2024
), Article ID:
85124
,
8
pages
10.12677/sa.2024.132045
高维因子模型两类“主成分”估计的比较
——以S & P 500股票数据分析为例
刘艺天
华南农业大学数学与信息学院,广东 广州
收稿日期:2024年3月26日;录用日期:2024年4月16日;发布日期:2024年4月24日

摘要
高维因子模型在超高维度的大型数据集降维处理中发挥了重要作用。目前,高维因子模型有两种主成分估计方法,分别是基于协方差的主成分估计PCE和基于滞后自协方差的主成分估计LPCE。本文以S & P 500公司股票数据的高维因子建模为例,比较了PCE和LPCE在高维股票数据降维中的实际表现,其中因子个数通过信息准则法和特征值比值估计法确定。结果表明,在高维非平稳序列因子模型中,PCE的均方根误差和预测误差都比LPCE小,PCE得到的因子也比LPCE更能捕捉高维非平稳序列变化特征。在高维平稳序列因子模型中,PCE和LPCE的估计误差相同,两者的估计因子均能还原高维平稳序列的变化特征。此外,在确定因子个数时,信息准则倾向于高估因子个数,表现出严重的过拟合。特征值比值估计法的估计结果相对更准确和稳定,在PCE中倾向于放弃相对弱势的主成分,在LPCE中则倾向于将弱势的主成分视为因子。
关键词
高维因子模型,主成分估计,信息准则,特征值比值估计

Comparison of Two Types of Principal Component Estimation in High-Dimensional Factor Model
—A Case Study of S & P 500 Stock Data Analysis
Yitian Liu
College of Mathematics and Information, South China Agricultural University, Guangzhou Guangdong
Received: Mar. 26th, 2024; accepted: Apr. 16th, 2024; published: Apr. 24th, 2024

ABSTRACT
High-dimensional factor models play a crucial role in dimensionality reduction of large datasets with ultra-high dimensions. Currently, there are two principal component methods for estimating high-dimensional factor models: Principal Component Estimation (PCE) based on covariance and Lagged Principal Component Estimation (LPCE) based on lagged autocovariance. This paper utilizes high-dimensional factor modeling of S & P 500 company stock data as a case study to compare the practical performance of PCE and LPCE in dimensionality reduction of high-dimensional stock data, where the number of factors is determined through the information criterion method and eigenvalue ratio method. Results indicate that in high-dimensional non-stationary sequence factor models, both the root mean square error and prediction error of PCE are smaller than LPCE. Additionally, factors obtained from PCE are more effective in capturing the characteristics of high-dimensional non-stationary sequence changes compared to LPCE. In high-dimensional stationary sequence factor models, the estimation errors of PCE and LPCE are identical, and both estimation methods can effectively capture the changing characteristics of high-dimensional stationary sequences. Furthermore, when determining the number of factors, the information criterion tends to overestimate the number of factors, indicating severe overfitting. The eigenvalue ratio method provides relatively more accurate and stable estimation results, with PCE tending to discard relatively weaker principal components, while LPCE tends to treat weaker principal components as factors.
Keywords:High-Dimensional Factor Model, Principal Component Estimation, Information Criterion, Eigenvalue Ratio Estimation

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
作为不同时间点记录的不同数据,对不同公司的股票数据建立标准的多元时间序列模型,如向量自回归模型,是研究者分析股票价格变化的重要模型。然而,进入大数据时代,对股票数据的收集越来越多,不仅体现在样本量大,而且体现在公司数量众多。此时,一些传统的数据分析手段往往会失效,例如,时间序列的维数N较大时,研究者建立的向量自回归模型将“维数灾难”问题,即模型中待估计参数的数量级往往达到N2,过度参数化会对模型识别产生严重的干扰,所建立的模型几乎不能实际应用。
目前,建立高维因子模型对高维数据集进行降维处理,再对低维因子作后续分析,已经成为研究者们分析大型数据集的常用手段之一。例如,廖春芳等人通过高维因子模型分析影响中国股市变化的潜在因素 [1] ;李伯龙利用高维分位数因子模型提取个股分位数变化的共同成分来衡量尾部系统风险 [2] 。郑红景等人建立高维动态因子模型对金融市场波动率进行建模 [3] 。
针对高维因子模型,基于某个非负定矩阵的特征分析技术获取模型的主成分估计是文献中使用最广泛的方法之一,与极大似然估计相比,主成分估计优势在于算法简单,估计结果具有稳健性,且不需要假设特殊因子相互独立和先验分布。目前,文献中对于高维因子模型的估计有两种截然不同的主成分估计,一是从可观测变量的截面信息出发,有基于最小二乘原理和协方差矩阵的主成分估计(PCE) [4] 。这一方法针对高维近似因子模型,对特殊因子的限制较少,允许异方差,弱序列相关,弱截面相关,也允许公共因子与特殊因子弱相关,非常宽松的假设条件使得该方法在计量经济学等领域被广泛使用。二是从可观测变量的滞后信息出发,有基于由可观测变量自协方差矩阵构建非负定矩阵的主成分估计(LPCE) [5] 。这一方法针对高维时间序列因子模型,理论上要求特殊因子是白噪声。虽然白噪声假设大多数情况下不太符合实际需要,但是从Lam等人针对时间序列因子模型建立的渐近理论来看,这一模型仍然具有以下理论上的优点,一是理论上可以在有限维情形下严格区分公共因子与特殊因子,二是允许特殊因子存在较强的截面相关性,三是允许因子与滞后噪声相关。此外,对于主成分估计,也存在两种因子个数的估计方法,一是基于惩罚函数的信息准则方法 [6] ,二是基于特征值极限性质的比值估计法 [7] [8] [9] 。
目前,这两类主成分估计在高维股票数据集中的表现缺乏直接的比较。对于不同的数据序列场景,两种主成分估计各自估计潜在的公共因子准确度如何,使用哪一种主成分估计所得到的公共因子能更好地还原众多原始股票的变化特征和预测其下一步的变化,是值得研究的问题。因此,本文以对标准普尔500指数(S & P 500)中包含的公司股票数据建立高维因子模型为例,比较高维因子模型中这两类不同的主成分估计的估计误差和预测误差,以及信息准则和特征值比值估计法在的因子个数估计上的表现。
本文的主要发现是,在高维非平稳时间序列因子模型中,PCE得到的估计因子的均方根误差和预测误差都比LPCE小。从图像上看,前者更能捕捉高维非平稳序列变化特征。在高维平稳时间序列因子模型中,PCE和LPCE的估计误差相同,两者的估计因子均能还原高维平稳序列的变化特征。此外,在确定因子个数时,特征值比值估计法在PCE中倾向于放弃相对弱势的主成分,在LPCE中则倾向于保留弱势的主成分作为弱因子。
2. 因子模型及估计方法介绍
2.1. 模型介绍
假设N维的可观测变量 已经中心化,即 。对于样本 ,经典因子模型结构如下, ,其中, , 是公因子,r是潜在公共因子的个数,满足 ; 是因子载荷矩阵,代表公共因子对于可观测变量的影响。 是N维特殊因子,代表系统中所有的随机误差。
将数据维数与样本数结合,可以将该模型重新表达为矩阵形式, ,其中, , , 。
目前,因子模型的不同主要体现在特殊因子的假设上。在经典因子模型中, ,即特殊因子是相互独立的,此时截面相关性全部来源于公共因子;在近似因子模型中, ,即允许特殊因子存在截面相关 [10] ;在时间序列因子模型中, ,即特殊因子是一个白噪声 [5] ,此时序列相关性全部来源于公共因子。
另外,因子模型的因子载荷矩阵与公共因子不具有唯一性,使用 替换 ,模型仍然成立。因此,在进行模型估计时会加上一个模型识别条件 或者 。
2.2. 主成分估计(PCE) [4]
PCE来源于在近似因子模型中求解如下优化问题,
,
这一优化问题等价于对样本协方差矩阵 进行特征分解。因子载荷矩阵的估计值为 ,其中 是矩阵 的第i大的特征值对应的特征向量。相应的因子得分为 。
2.3. 基于自协方差矩阵的主成分估计(LPCE) [5]
LPCE来源于时间序列因子模型,此时特殊因子是白噪声。对于任意 ,定义 , ,有 。对于常数 ,定义矩阵
,
此时, 由M的非零特征值对应的特征向量张成。因此,因子载荷矩阵估计值为 ,相应因子得分为 。其中, 是 第i大的特征值对应的特征项对应的特征向量, 。
2.4. 因子个数估计
因子载荷矩阵的PCE和LPCE都是某个非负定矩阵的特征向量构成,因此因子个数的估计实际上是选择几个主成分作为公共因子的问题。
信息准则BIC和CPp1通过为最小二乘的目标函数加入惩罚函数来选择最佳的因子个数 [6] 。假设选择k个因子 ,具体形式为
BIC准则: ,
CPp1准则: ,
其中, 是估计误差的样本平均值。
特征值比值估计法基于公共因子的特征值会随N和T发散到无穷,而其余特征值的始终有界,通过定位相邻特征值的比值突变处估计因子个数。假设主成分估计对应的特征值为 ,有如下三种比值估计法,
ER估计 [7] : ,
GR估计 [8] : ,
TCR估计 [9] : 。
3. 实证分析
3.1. 数据选择与预处理
本文选择S & P 500指数中480只股票在2013年1月1日至2023年12月31日期间的每日收盘价 ,数据来源于雅虎财经。这一案例中,变量维数 ,样本量 。本文对数据进行两种预处理,一是的对数日收盘价 ,二是对数日收益率 ,表达式分别为:
, 。
表1给出了两种数据的ADF检验结果,在5%的显著性水平下,对数日收盘价 是非平稳数据,而对数日收益率 是平稳序列。
Table 1. Mean of ADF test statistic for data series of 480 stocks of S & P 500 index
表1. S & P 500指数480只股票数据序列ADF检验统计量均值
3.2. 因子个数估计
表2给出了PCE估计和LPCE估计中分别使用信息准则和特征值比值估计法估计因子个数的结果。表3则给出了前5个主成分估计值对应的特征值,因为各主成分对应的特征值实际上反映了其对可观测变量方差的贡献,所以特征值的相对大小可用于辅助判断因子个数。
Table 2. The estimation of factor number
表2. 因子个数估计结果
Table 3. Principal components correspond to the top 5 eigenvalues
表3. 主成分对应的前5大特征值
对于非平稳序列 ,信息准则BIC和CPp1倾向于给出15个因子,这是本文设置的最大因子个数,说明信息准则法会严重高估因子个数。特征值比值估计法的表现相对良好,在PCE中ER、GR和TCR都估计1个因子。在LPCE中ER估计1个因子,GR和TCR估计2个因子,结合表3,在PCE得到主成分中,第一主成分比其余主成分贡献度高两个数量级,其余主成分处于同一个数量级。在LPCE中,第一主成分的贡献度处于绝对强势地位;第二主成分是弱因子,比剩余主成分高一个数量级,可以视为弱因子。
对于平稳序列 ,在PCE中,BIC和CPp1估计5个和15个因子,ER、GR和TCR都估计2个因子,此时信息准则仍然高估因子个数。在LPCE中,BIC和GR与TCR估计3个因子,而CPp1高估因子个数,ER低估因子个数。结合表3,可以确定存在2~3个因子。
综合来看,使用对数日收盘价 建模,存在1~2个因子;使用对数日收益率 建模,存在2~3个因子。并且,在PCE和LPCE两种估计方法中,第一因子都远强于其余因子,可以解释为美股中的市场因素;较弱的第二因子和第三因子可以解释为政府政策因素和行业因素。
3.3. 因子得分
图1给出了对数日收盘价 的因子模型中PCE和LPCE的第一因子得分与S & P 500对数指数的变化趋势。图2给出了对数日收益率 的因子模型中PCE和LPCE的第一因子得分与S & P 500对数差分指数的变化趋势。
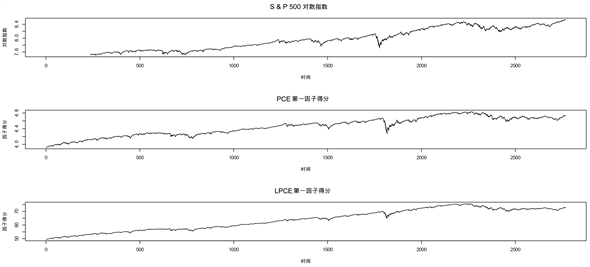
Figure 1. Trends in the first factor of log daily closing prices versus the S & P 500 log index
图1. 对数日收盘价vt第一因子与S & P 500对数指数的变化趋势
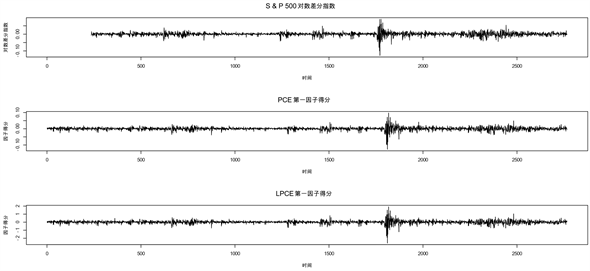
Figure 2. Trends in the first factor of log daily returns versus the S & P 500 log difference index
图2. 对数日收益率rt第一因子与S & P 500对数差分指数的变化趋势
通过观察图1和图2,对于非平稳序列 ,PCE的第一因子相比LPCE的第一因子更准确的捕捉了S & P 500对数指数在某些时间节点的突变特征。而对于平稳序列 ,PCE和LPCE的表现相同,都很好地还原了S & P 500对数差分指数的变化特征。
3.4. 估计误差
本文使用均方根误差(RMSE)和预测误差(FE)两个指标比较PCE和LPCE的总体估计表现。RMSE和FE的定义如下, , ,其中, ; 是 的样本预测值,利用 建立VAR (1)模型并向前一步预测得到。表4和表5分别给出了当因子个数取1至3个时,PCE和LPCE两种方法在RSEM和FE上的结果。
Table 4. Root mean square error
表4. 均方根误差
Table 5. Forecast error
表5. 预测误差
可以看到,对于非平稳序列 ,PCE的表现比LPCE好很多,无论是样本均方根误差还是向前一步的预测误差,PCE的结果都比LPCE小一个数量级。对于平稳序列 ,PCE和LPCE的估计误差很接近,几乎没有区别。
进一步,从RMSE和FE在不同因子个数下的结果也间接反映了前文中关于因子个数的讨论结果。具体来看,对于 ,PCE的RMSE和FE都在因子个数为1时最小,LPCE都在因子个数为2时最小;对于 ,PCE的RMSE和FE都在因子个数为2时最小,LPCE都在因子个数为3时最小。
4. 结论
结合全部实证分析的结果,对于高维因子模型,可以得到以下结论。
当可观测序列是高维非平稳时间序列,使用基于截面信息的PCE进行模型估计要比基于滞后信息的LPCE更好,此时PCE的样本均方误差和向前一步预测误差都比LPCE小一个数量级。进一步看,PCE因子不仅可以准确还原原始序列的时间趋势,还能精确捕捉它在某些时间点上的突变特征,而LPCE仅能大致还原原始序列的趋势,没有很好地反映它的突变特征。
当可观测序列是高维平稳时间序列,在模型估计中PCE和LPCE均可以使用,两者的样本均方误差和向前一步预测误差几乎相同,此时两者的因子估计值均可以还原原始序列的波动趋势,并且准确地捕捉了其中的异常波动。
对于因子个数的估计,信息准则在高维非平稳序列因子模型中会非常容易过拟合,表现为严重高估因子个数,而在高维平稳序列因子模型中表现会好很多,但仍然会倾向高估因子个数。特征值比值估计法对原始序列的平稳性不敏感,估计结构具有稳健性,其中,ER估计倾向于低估因子个数,GR和TCR的结果更具有说服力,可以识别可能是因子的弱势主成分。
此外,特征值比值估计法在PCE和LPCE上的结果也有差异。当主成分之间的方差贡献度有明显强弱之分,但差距不超过一个数量级时,比值估计法在PCE上倾向于放弃弱势的主成分,而在LPCE上则倾向于将弱势的主成分视为弱因子。
文章引用
刘艺天. 高维因子模型两类“主成分”估计的比较——以S & P 500股票数据分析为例
Comparison of Two Types of Principal Component Estimation in High-Dimensional Factor Model—A Case Study of S & P 500 Stock Data Analysis[J]. 统计学与应用, 2024, 13(02): 453-460. https://doi.org/10.12677/sa.2024.132045
参考文献
- 1. 廖春芳, 刘金山. 基于贝叶斯方法的高维因子模型在中国股市的应用[J]. 佛山科学技术学院学报(自然科学版), 2016, 34(6): 31-36.
- 2. 李伯龙. 基于高维分位数因子模型的中国股市尾部系统风险分析[J]. 系统管理学报, 2021, 30(6): 1079-1087.
- 3. 郑红景, 蒋梦梦, 周杰. 股票市场的高维动态因子模型及其实证分析[J]. 计算机工程与应用, 2020, 56(12): 243-249.
- 4. Bai, J. (2003) Inferential Theory for Factor Models of Large Dimensions. Econometrica, 71, 135-171. https://doi.org/10.1111/1468-0262.00392
- 5. Lam, C., Yao, Q. and Bathia, N. (2011) Estimation of Latent Factors for High-Dimensional Time Series. Biometrika, 98, 901-918. https://doi.org/10.1093/biomet/asr048
- 6. Bai, J. and Ng, S. (2002) Determining the Number of Factors in Approximate Factor Models. Econometrica, 70, 191-221. https://doi.org/10.1111/1468-0262.00273
- 7. Lam, C. and Yao, Q. (2012) Factor Modeling for High-Dimensional Time Series: Inference for the Number of Factors. The Annals of Statistics, 40, 694-726. https://doi.org/10.1214/12-AOS970
- 8. Ahn, S.C. and Horenstein, A.R. (2013) Eigenvalue Ratio Test for the Number of Factors. Econometrica, 81, 1203-1227. https://doi.org/10.3982/ECTA8968
- 9. Xia, Q., Liang, R. and Wu, J. (2017) Transformed Contribution Ratio Test for the Number of Factors in Static Approximate Factor Models. Computational Statistics & Data Analysis, 112, 235-241. https://doi.org/10.1016/j.csda.2017.03.005
- 10. Chamberlain, G. and Rothschild, M. (1983) Arbitrage, Factor Structure, and Mean-Variance Analysis on Large Asset Markets. Econometrica, 51, 1281-1304. https://doi.org/10.2307/1912275
