Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21472,8
pages
10.12677/AAM.2017.64071
Well-Balanced Central Discontinuous Galerkin Methods for the Nonlinear Shallow Water Equations
Aimin Chen1, Maojun Li2
1City College of Science and Technology, Chongqing University, Chongqing
2College of Mathematics and Statistics, Chongqing University, Chongqing

Received: Jul. 1st, 2017; accepted: Jul. 21st, 2017; published: Jul. 25th, 2017

ABSTRACT
A high order well-balanced central discontinuous Galerkin method is developed for solving the nonlinear shallow water equations and the well-balanced property is proved. Compared to the standard central discontinuous Galerkin method, the present method can maintain the still water stationary solutions of the nonlinear shallow water equations, and thus remove the numerical oscillations. Numerical examples are presented to show the accuracy and reliability of the proposed method.
Keywords:Central Discontinuous Galerkin Method, Nonlinear Shallow Water Equations, Well-Balanced Property
非线性浅水波方程的保持平衡的 中心间断伽辽金法
陈爱敏1,李茂军2
1重庆大学城市科技学院,重庆
2重庆大学数学与统计学院,重庆
收稿日期:2017年7月1日;录用日期:2017年7月21日;发布日期:2017年7月25日

摘 要
提出了一个求解非线性浅水波方程的高阶的保持平衡的中心间断伽辽金法,并证明了该方法的保持平衡性。与传统的中心间断伽辽金法相比,该方法能够精确地保持非线性浅水波方程的静水稳定解,因而消除了数值震荡。数值算例验证了方法的精度和可靠性。
关键词 :中心间断伽辽金法,非线性浅水波方程,保持平衡性

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
非线性浅水波方程 [1] 在与河流,湖泊,沿海区域的流体流动有关的科学工程问题中有广泛的应用,例如海啸和风暴的预报,河口和近海水域的潮汐能捕捉等。由于问题是非线性的且问题的解有不连续的情况,因而数值求解非线性浅水波方程具有很大的挑战性。在一般情况下,非线性浅水波方程是一类平衡律,这类方程具有静水稳定解,对该稳定解,流通项非零但被源项所平衡,然而通常的数值方法不能保持流通项和源项的平衡,从而不能保持稳定解,因此在计算与稳定解相关的问题时常常会产生数值伪震荡。在最近几十年,已经出现了许多求解非线性浅水波方程的保持静水稳定解的数值方法 [1] [2] [3] [4] [5] ,这样的方法被称为保持平衡的方法。本文的目的是基于求解一般守恒律的中心间断伽辽金法 [6] ,提出一个高阶的保持平衡的中心间断伽辽金法(WBCDGM)来求解非线性浅水波方程,该方法通过引入一个参数来改写方程,然后再将中心间断伽辽金法应用到改写后的方程,当我们对参数取合适的值时,数值格式在保持高阶精度的同时,也保持了静水稳定解,从而消除了数值伪震荡。
2. 非线性浅水波方程
考虑如下的一维非线性浅水波方程:
 (1)
(1)
其中 ,
, 是未知函数,
是未知函数, 表示流通函数,
表示流通函数,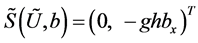 表示源项,
表示源项, 表示水的深度,
表示水的深度,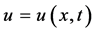 表示水的速度,
表示水的速度, 表示重力加速度,
表示重力加速度,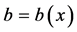 表示底部地势。
表示底部地势。
非线性浅水波方程(1)有如下的静水稳定解:
 (2)
(2)
其中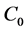 为常数,
为常数, 表示水面高度。从(1)能够观察到,在流体为静止状态,即(2)式成立时,且底部地势
表示水面高度。从(1)能够观察到,在流体为静止状态,即(2)式成立时,且底部地势 不是常数时,流通函数的导数非零但是其刚好被源项所抵消。
不是常数时,流通函数的导数非零但是其刚好被源项所抵消。
3. 数值方法
假设 是空间区域
是空间区域 的一个单元剖分,
的一个单元剖分,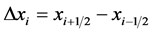 是
是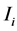 的长度,
的长度, 是网格大小。让
是网格大小。让 ,那么
,那么 是与
是与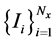 相互重叠的网格。在这两套网格上,我们定义如下的有限维离散空间:
相互重叠的网格。在这两套网格上,我们定义如下的有限维离散空间:

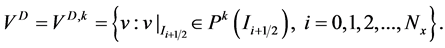
其中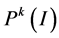 表示定义在区间
表示定义在区间 上的次数至多为
上的次数至多为 的多项式空间。另外让
的多项式空间。另外让 表示时间区域
表示时间区域 的一个剖分,定义
的一个剖分,定义 ,
,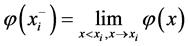 。
。
若直接使用中心间断伽辽金法 [6] 去离散方程(1),则所得到的数值格式对静水稳定解(2)不能精确成立,因此数值结果会产生数值伪震荡,为了避免该问题,我们首先将(1)改写为:
 (3)
(3)
其中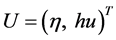 ,
, ,
, ,
, 是一个待定参数。
是一个待定参数。
然后使用中心间断Galerkin法 [6] 去离散(3)的空间变量,使用向前欧拉法去离散时间变量,即求 ,
, ,使得对任意的
,使得对任意的 和
和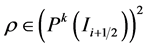 下面的方程成立:
下面的方程成立:
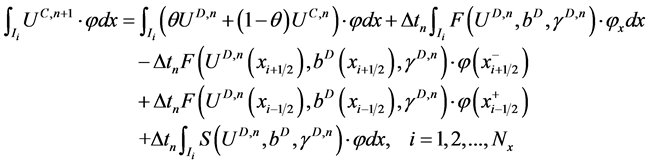 (4)
(4)
 (5)
(5)
其中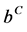 ,
, 是
是 分别在
分别在 ,
, 中的
中的 投影,
投影, ,
, 分别是数值解
分别是数值解 在
在 时刻的值,
时刻的值, ,
,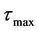 是由CFL条件所限制的时间步长的一个上限。
是由CFL条件所限制的时间步长的一个上限。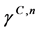 和
和 是参数
是参数 在
在 时刻的近似值,为了让数值格式(4)和(5)对静水稳定解(2)精确成立,必须选择合适的
时刻的近似值,为了让数值格式(4)和(5)对静水稳定解(2)精确成立,必须选择合适的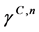 和
和 ,最好的选择是
,最好的选择是 ,但对一般的问题,
,但对一般的问题, 是未知的,因此在本文提出的数值格式中
是未知的,因此在本文提出的数值格式中 和
和 分别被定义为:
分别被定义为:
 (6)
(6)
我们将所提出的算法(4)~(6)命名为保持平衡的中心间断伽辽金法(WBCDGM),而直接将中心间断伽辽金法应用到方程(1)得到的算法命名为非保持平衡的中心间伽辽金法(NWBCDGM)。现在,我们有如下的定理:
定理1 全离散形式的中心间断伽辽金法(4)~(6)精确地满足静水稳定解(2)。
证明:因为在初始时刻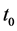 ,
,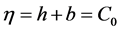 ,
, ,那么通过
,那么通过 投影可以得到
投影可以得到 。现在假设在
。现在假设在 时刻,
时刻,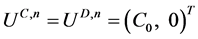 ,那么我们想要证明
,那么我们想要证明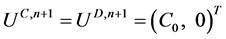 。
。
因为 ,那么方程(4)的右端第一项为:
,那么方程(4)的右端第一项为:
 (7)
(7)
由于 ,则由(6)知
,则由(6)知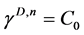 ,那么
,那么


因此对(6)右端第二项到第五项,我们有
 (8)
(8)
最后将(7)和(8)带入(4)式可得:

取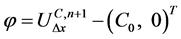 ,可得
,可得 。同理可证
。同理可证 。定理证毕。
。定理证毕。
4. 数值算例
为了便于表述,我们在上一部分使用了向前欧拉法来离散时间变量,但为了增加时间上的计算精度以及保持算法的稳定性,我们在计算中均使用三阶的Runge-Kutta法来离散时间变量,该方法是向前欧拉法的凸组合,因此仍旧保持了算法原有的性质。时间步长被动态的选择:

其中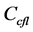 所谓的CFL数,对
所谓的CFL数,对 的情况,我们取
的情况,我们取 ,而对
,而对 的情况我们取
的情况我们取 。在所有的算例中,所有变量都被无因化,因此取重力加速度
。在所有的算例中,所有变量都被无因化,因此取重力加速度 。此外,对所有测试我们取
。此外,对所有测试我们取 ,即
,即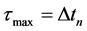 。
。
在这一部分,我们选择一些算例来验证保持平衡的中心间断伽辽金法的精确性和可靠性,并与传统的中心间断伽辽金法的结果进行了对比。对解为非光滑的算例,我们使用TVB minmod限制器来维持解的稳定性,并始终选取TVB minmod限制器中的常数 。在保持平衡的中心间断伽辽金法中,该限制器被直接执行在
。在保持平衡的中心间断伽辽金法中,该限制器被直接执行在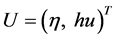 上,因此其并不破坏算法的保持平衡性。
上,因此其并不破坏算法的保持平衡性。
算例1. 静水稳定解
作为第一个算例,我们检测所提出的算法是否精确的保持静水稳定解。我们使用的稳定解为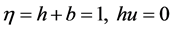 ,底部地势为
,底部地势为 。计算区域为
。计算区域为 被划分为50个均匀的网格。我们使用单精度和双精度两种精度类型进行了计算,我们计算到
被划分为50个均匀的网格。我们使用单精度和双精度两种精度类型进行了计算,我们计算到 。数值解的误差如表1所示。所有误差均在相应精度类型的计算机误差水平,因此所提出的算法确实能够保持静水稳定解。
。数值解的误差如表1所示。所有误差均在相应精度类型的计算机误差水平,因此所提出的算法确实能够保持静水稳定解。
算例2. 精度测试
在这个算例中,我们检测所提出算法的高阶精度。我们考虑如下的初始条件和底部地势:
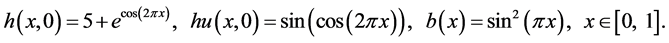
边界条件是周期的。由于精确解未知,我们使用8000个均匀网格上的数值解作为参考解来计算误差。计算结果如表2所示。从表2可以看出,当我们加密网格,所提出的算法是收敛的,而且对分片线性近似我们得到了二阶的收敛精度,对分片二次多项式近似,我们得到了三阶的收敛精度。因此,所提出的算法具有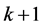 阶的收敛精度
阶的收敛精度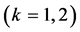 ,即该方法具有最优收敛阶。
,即该方法具有最优收敛阶。
算例3. 稳定解的扰动
在这个算例中,我们考虑一个稳定解的扰动,即初始条件为:

其中 是一个小的非零扰动,底部地势是一个拱形,即:
是一个小的非零扰动,底部地势是一个拱形,即:

为了方便观察初始条件的情况,我们将其描绘在图1中。其他这个算例被使用来检测所提出的算法在模拟快速变化流体的能力,我们同时也利用非保持平衡的中心间断伽辽金法来计算该问题,以便观察两个方法的计算结果的差别。
我们考虑了两个扰动:一个较大的扰动 和一个较小的扰动
和一个较小的扰动 。理论上,对一个非零扰动,其将分裂为两个波,一个以速度
。理论上,对一个非零扰动,其将分裂为两个波,一个以速度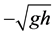 (负号表示向左的方向)向左传播,一个以速度
(负号表示向左的方向)向左传播,一个以速度 向右传播。许多数值方法很难去模拟这样的波的传播,特别是当扰动特别小的时候。两种方法的数值结果分别描绘在了图2~图5中。
向右传播。许多数值方法很难去模拟这样的波的传播,特别是当扰动特别小的时候。两种方法的数值结果分别描绘在了图2~图5中。
我们在粗细两套网格上进行了计算,两个方法的解都收敛到同一个解。但是,从这些图片中,我们可以看出中心间断Galerkin法在使用粗糙网格的时候不能很好的模拟这个问题,特别是对较小的扰动,这是因为该方法不能平衡流通项和源项,从而在底部不平坦的地方产生了数值震荡,为了得到较好的结果,只能加密网格,然而这将使得计算费用增加,而且这也只能使得震荡减小,却不会消失。而保持平衡的中心间断Galerkin法即使在使用粗糙网格的时候也能得到没有数值震荡的结果。
5. 结论
在这篇文章中,我们研究了一维非线性浅水波方程的数值方法,提出了一个保持平衡的中心间断伽辽金法,该方法具有高阶精度而且能够保持静水稳定解。该方法也能够容易地推广到二维情况。在未来的研究工作中,我们进一步将该方法推广到其他水波方程,例如非线性弱色散的浅水波方程——Green-Naghdi模型。
Table 1. Errors of numerical solutions for Example 1
表1. 算例1的数值结果的误差
Table 2. Errors and convergence orders of numerical solutions for Example 2
表2. 算例2的数值解的误差和收敛阶

Figure 1. Initial conditions and bottom of Example 3. Dashed line: initial conditions; Solid line: bottom
图1. 算例3的初始条件和底部。虚线:初始条件;实线:底部

Figure 2. NWBCDGM numerical solutions for perturbation . Dot: 200 elements; solid line: 2000 elements
. Dot: 200 elements; solid line: 2000 elements
图2. 扰动 的NWBCDGM数值解。实点:200单元的解;实线:2000单元上的解
的NWBCDGM数值解。实点:200单元的解;实线:2000单元上的解
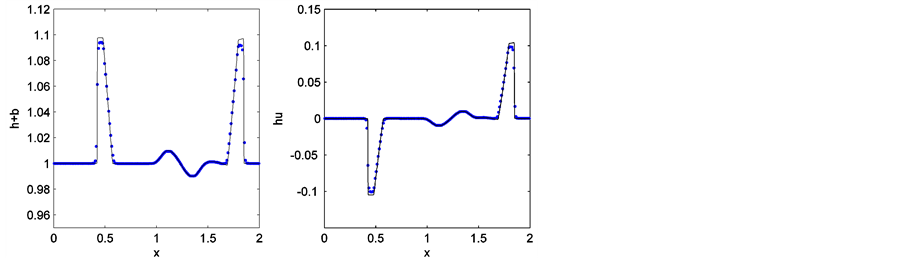
Figure 3. WBCDGM numerical solutions for perturbation . Dot: 200 elements; solid line: 2000 elements
. Dot: 200 elements; solid line: 2000 elements
图3. 扰动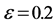 的WBCDGM数值解。实点:200单元的解;实线:2000单元上的解
的WBCDGM数值解。实点:200单元的解;实线:2000单元上的解

Figure 4. NWBCDGM numerical solutions for perturbation 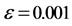 . Dot: 200 elements; Solid line: 2000 elements
. Dot: 200 elements; Solid line: 2000 elements
图4. 扰动 的NWBCDGM数值解。实点:200单元的解;实线:2000单元上的解
的NWBCDGM数值解。实点:200单元的解;实线:2000单元上的解

Figure 5. WBCDGM numerical solutions for perturbation . Dot: 200 elements; Solid line: 2000 elements
. Dot: 200 elements; Solid line: 2000 elements
图5. 扰动 的WBCDGM数值解。实点:200单元的解;实线:2000单元上的解
的WBCDGM数值解。实点:200单元的解;实线:2000单元上的解
基金项目
重庆市教育科学“十三五”规划课题(课题编号:2016-GX-163)国家自然科学基金青年基金(项目编号: 11501062)。
文章引用
陈爱敏,李茂军. 非线性浅水波方程的保持平衡的中心间断伽辽金法
Well-Balanced Central Discontinuous Galerkin Methods for the Nonlinear Shallow Water Equations[J]. 应用数学进展, 2017, 06(04): 611-618. http://dx.doi.org/10.12677/AAM.2017.64071
参考文献 (References)
- 1. Xing, Y. and Shu, C.-W. (2005) High Order Finite Difference WENO Schemes with the Exact Conservation Property for the Shallow Water Equations. Journal of Computational Physics, 208, 206-227. https://doi.org/10.1016/j.jcp.2005.02.006
- 2. Xing, Y. and Shu, C.-W. (2006) High Order Well-Balanced Finite Volume WENO Schemes and Discontinuous Galerkin Methods for a Class of Hyperbolic Systems with Source Terms. Journal of Computational Physics, 214, 567-598. https://doi.org/10.1016/j.jcp.2005.10.005
- 3. Michel-Dansac, V., Berthon, C., Clain, S. and Foucher, F. (2016) A Well-Balanced Scheme for the Shallow-Water Equations with Topography. Computers & Mathematics with Applications, 72, 568-593. https://doi.org/10.1016/j.camwa.2016.05.015
- 4. Li, M., Guyenne, P., Li, F. and Xu, L. (2017) A Positivity-Preserving Well-Balanced Central Discontinuous Galerkin Method for the Nonlinear Shallow Water Equation. Journal of Scientific Computing, 71, 994-1034. https://doi.org/10.1007/s10915-016-0329-z
- 5. Zhu, Q., Gao, Z., Don, W.S. and Lv, X. (2017) Well-Balanced Hybrid Com-pact-WENO Scheme for Shallow Water Equations. Applied Numerical Mathematics, 112, 65-78. https://doi.org/10.1016/j.apnum.2016.10.001
- 6. Liu, Y., Shu, C.-W., Tadmor, E. and Zhang, M. (2007) Central Discontinuous Galerkin Methods on Overlapping Cells with a Nonoscillatary Hierarchical Reconstruction. SIAM Journal on Numerical Analysis, 45, 2442-2467. https://doi.org/10.1137/060666974
