Advances in Applied Mathematics
Vol.
13
No.
04
(
2024
), Article ID:
85088
,
10
pages
10.12677/aam.2024.134132
非线性时间分数阶四阶混合次扩散和扩散波动方程的混合有限元算法
杨宁
内蒙古大学数学科学学院,内蒙古 呼和浩特
收稿日期:2024年3月19日;录用日期:2024年4月16日;发布日期:2024年4月23日

摘要
本文数值求解了一个二维非线性时间分数阶四阶混合次扩散和扩散波动方程,在时间方向上采用L1-CN格式,在空间上通过混合有限元方法进行离散,并且在此基础上,给出了它的全离散格式。最后针对该数值格式提供了算法过程和数值算例,以及详细的收敛结果。
关键词
非线性时间分数阶四阶混合次扩散和扩散波动方程,L1-CN格式,混合有限元方法,数值算例

Mixed Finite Element Algorithm for a Nonlinear Time-Fractional Fourth-Order Mixed Sub-Diffusion and Diffusion Wave Equation
Ning Yang
School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia
Received: Mar. 19th, 2024; accepted: Apr. 16th, 2024; published: Apr. 23rd, 2024

ABSTRACT
In this article, the two-dimensional nonlinear time-fractional fourth-order mixed sub-diffusion and diffusion wave equation is numerically solved, where L1-CN scheme is used in the time direction, and the mixed finite element method is applied in space. Further, the fully discrete scheme is provided. Finally, the algorithm process, numerical example, and detailed convergence results are provided for this numerical scheme.
Keywords:Nonlinear Time-Fractional Fourth-Order Mixed Sub-Diffusion and Diffusion Wave Equation, L1-CN Scheme, Mixed Finite Element Method, Numerical Example

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分数阶扩散方程作为分数阶偏微分方程的一个重要组成部分,常被用于解释不同物质之间的扩散现象,随着研究深入,含扩散项的方程不断演变,其中带有单个时间分数阶的扩散类方程最为常见,时间分数阶为Caputo型 [1] [2] [3] [4] 或Riemann-Liouville型 [5] [6] 居多。
随着研究更加深入,人们发现带有两项时间分数阶的扩散或扩散波动方程更能准确地把握物质的属性以及现象发生的过程。在 [7] 中,Feng等利用有限元方法首次研究了二维时间分数阶混合次扩散和扩散波动方程。近些年混合次扩散和扩散波动方程的研究理论不断完善,其中,Chen等 [8] 利用空间两网格有限元方法结合L1-CN格式解决了一个二维非线性时间分数阶两项混合次扩散和扩散波动方程。在 [3] 中,Sun等将有限差分法与L1格式相结合数值离散了一个分数阶混合次扩散和扩散波动方程。在 [9] 中,Shen等将单项时间分数阶扩散波动方程的H2N2方法扩展到带有非齐次原项的时间分数阶混合次扩散和扩散波动方程上。由此可知,L1-CN格式及其改进格式能有效求解混合次扩散和扩散方程。除此之外,不同形式的双分数阶方程多年来同样被大量学者重视。在 [10] 中,Yin等人在卷积求积框架下,利用Caputo型分数阶导数与Riemann-Liouville型分数阶导数的关系化解了系数为(1, 2)的分数阶导数卷积求解难的问题。纵然双分数阶问题被大量研究,但多年来该问题的四阶情况从未被考虑,因此选取合适的数值方法来处理含有四阶项的双分数阶问题具有非常重要的意义。据了解目前处理高阶问题常用的方法有混合有限元方法 [11] [12] ,有限差分法 [13] ,间断有限元方法 [14] 等。
在本文中,我们在空间上选用混合有限元方法,在时间上利用L1-CN格式考虑以下二维非线性四阶时间分数阶混合次扩散和扩散波动方程:
(1)
满足边界条件
(2)
和初始条件
(3)
其中 , 是一个凸多边形区域, 是 的边界, 是时间区间,并且 。
和 均为Caputo型分数阶导数,有如下定义:
本文的重点如下:
1) 二维非线性时间分数阶四阶混合次扩散和扩散波动方程首次被研究。
2) 本文以混合有限元和L1-CN格式相结合的方法处理四阶混合次扩散和扩散波动方程。同时还呈现了该方程详细的混合有限元算法过程,以及算例和数据结果。
本文结构如下:
在第二节中,通过引入辅助变量 ,将四阶问题转化为二阶耦合系统,然后时间方向上结合L1-CN近似公式给出相对应的全离散格式。在第三节中,基于耦合系统的全离散格式,给出方程(1)~(3)的详细算法过程,并呈现了算例的误差和收敛结果。在第四节中,得出了一些结论。
2. 数值格式
在这一节中,我们在时间方向上利用L1-CN近似公式的引理结合空间混合有限元方法得出方程(1)~(3)的弱形式和全离散格式。
为了得到全离散格式,我们将时间区间 均匀剖分为 ,N为正整数,其中 , 为时间步长。定义 ,我们给出 处的几个离散形式:
引理1
Caputo型导数 和 的L1-CN近似公式 [4] [8] 如下所示:
其中 , , 。
接下来引入一个辅助变量 ,方程(1)可以改写为:
(4)
(5)
取 , ,(4)~(5)在 处相应的弱形式如下:
定义有限元空间 和
利用引理1,取 , ,其中 ,可以得到以下全离散格式:
(6)
(7)
3. 数值模拟
3.1. 数值算法
对 , ,且 , ,我们记,
然后有
故令
进而对于(6)~(7)有以下算法方程式成立:
当 时,
其中
当 时,
其中
3.2. 数值算例
在本节中,通过数值算例验证数值格式的有效性。
以下方程的精确解表示为 ,
其中 , , 是已知源项
在表1中,固定时间步长 ,选择空间网格步长 ,得到了基于不同参数 , , , 以及 , 下的空间收敛结果。在表2中,固定空间网格步长 ,选择时间步长 ,得到了基于不同参数 , , , 以及 , 下的时间收敛结果。表1,表2的收敛结果表明数值格式(6)~(7)对于求解方程(1)~(3)是非常有效的。
Table 1. Spatial convergence results with τ = 1 / 400
表1. 当 时,空间收敛结果
Table 2. Time convergence results with H = 1 / 32400
表2. 当 时,空间收敛结果
为了更加直观清楚地观察数值模拟的效果,给出了一些数值解以及误差的图像。图1~3展示了精确解u和数值解 基于不同参数 和 的图像。在图4,图5中,给出了不同参数 和 下的 和 的等高线图。最后在图6,图7中,我们结合表1,表2的数据分别画出了 和 的空间收敛阶图和时间收敛阶图。
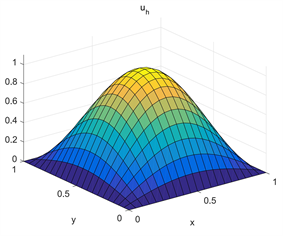
Figure 1. The images of numerical solution and exact solution u with ,
图1. 当 , 数值解 与精确解u的图像
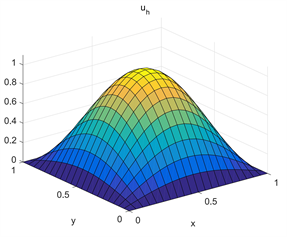
Figure 2. The images of numerical solution and exact solution u with ,
图2. 当 , 数值解 与精确解u的图像
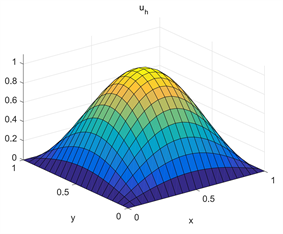
Figure 3. The images of numerical solution and exact solution u with ,
图3. 当 , 数值解 与精确解u的图像
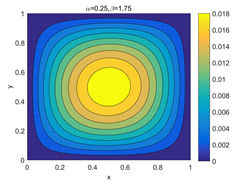
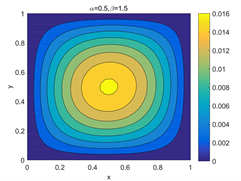
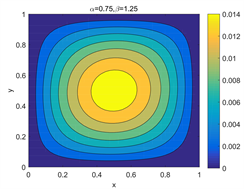
Figure 4. Error contour of with different parameters and
图4. 不同参数 和 下, 的误差等高线图
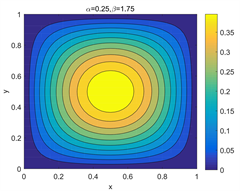
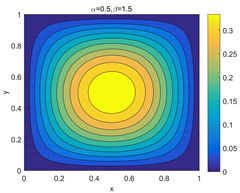
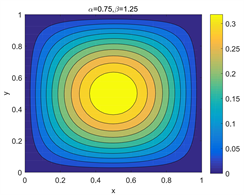
Figure 5. Error contour of
with different parameters  and
and
图5. 不同参数 和 下, 的误差等高线图
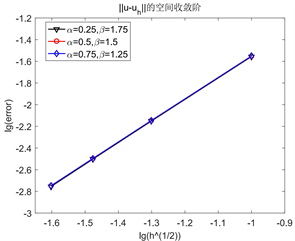
Figure 6. Spatial convergence order of and with different parameters and
图6. 不同参数 和 下, 和 的空间收敛阶图
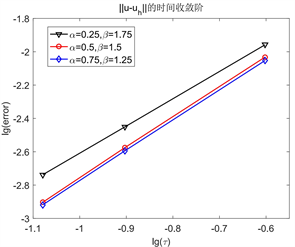
Figure 7. Spatial convergence order of and with different parameters and
图7. 不同参数 和 下, 和 的时间收敛阶图
4. 结论
本文提出了一种数值求解二维非线性时间分数阶四阶混合次扩散和扩散波动方程的方法,具体是在空间方向上采用混合有限元方法,在时间方向上利用L1-CN格式。进一步给出了它的全离散格式以及混合有限元算法过程。最后通过算例及其结果表明我们的方法能够有效地求解含有四阶导数项的混合次扩散和扩散波动方程。
文章引用
杨 宁. 非线性时间分数阶四阶混合次扩散和扩散波动方程的混合有限元算法
Mixed Finite Element Algorithm for a Nonlinear Time-Fractional Fourth-Order Mixed Sub-Diffusion and Diffusion Wave Equation[J]. 应用数学进展, 2024, 13(04): 1415-1424. https://doi.org/10.12677/aam.2024.134132
参考文献
- 1. Liu, Y., Du, Y. and Li, H. (2015) A Two-Grid Mixed Finite Element Method for a Nonlinear Fourth-Order Reaction-Diffusion Problem with Time-Fractional Derivative. Computers & Mathematics with Applications, 70, 2474-2492. https://doi.org/10.1016/j.camwa.2015.09.012
- 2. Lin, Y. and Xu, C. (2007) Finite Difference/Spectral Approximations for the Time-Fractional Diffusion Equation. Journal of Computational Physics, 225, 1533-1552. https://doi.org/10.1016/j.jcp.2007.02.001
- 3. Sun, Z.Z., Ji, C.C. and Du, R.L. (2020) A New Analytical Technique of the L-Type Difference Schemes for Time Fractional Mixed Sub-Diffusion and Diffusion-Wave Equations. Applied Mathematics Letters, 102, 106115. https://doi.org/10.1016/j.aml.2019.106115
- 4. Sun, Z.Z. and Wu, X.N. (2006) A Fully Discrete Difference Scheme for a Diffusion-Wave System. Applied Numerical Mathematics, 56, 193-209. https://doi.org/10.1016/j.apnum.2005.03.003
- 5. Liu, N., Liu, Y., Li, H. and Wang, J. (2018) Time Second-Order Finite Difference/Finite Element Algorithm for Nonlinear Time-Fractional Diffusion Problem with Fourth-Order Derivative Term. Computers & Mathematics with Applications, 75, 3521-3536. https://doi.org/10.1016/j.camwa.2018.02.014
- 6. Yin, B.L., Liu, Y. and Li, H. (2020) A Class of Shifted High-Order Numerical Methods for the Fractional Mobile/Immobile Transport Equations. Applied Mathematics and Computation, 368, 124799. https://doi.org/10.1016/j.amc.2019.124799
- 7. Feng, L.B., Liu, F.W. and Turner, I. (2019) Finite Difference/Finite Element Method for a Novel 2D Multi-Term Time-Fractional Mixed Sub-Diffusion and Diffusion-Wave Equation on Convex Domains. Communications in Nonlinear Science and Numerical Simulation, 70, 354-371. https://doi.org/10.1016/j.cnsns.2018.10.016
- 8. Chen, Y., Gu, Q., Li, Q. and Huang, Y. (2022) A Two-Grid Finite Element Approximation for Nonlinear Time Fractional Two-Term Mixed Sub-Diffusion and Diffusion Wave Equations. Journal of Computational Mathematics, 40, 936. https://doi.org/10.4208/jcm.2104-m2021-0332
- 9. Shen, J.Y. and Gu, X.M. (2022) Two Finite Difference Methods Based on an H2N2 Interpolation for Two-Dimensional Time Fractional Mixed Diffusion and Diffusion-Wave Equations. Discrete and Continuous Dynamical Systems B, 27, 1179-1207. https://doi.org/10.3934/dcdsb.2021086
- 10. Yin, B.L., Liu, Y., Li, H. and Zeng, F.H. (2021) A Class of Efficient Time-Stepping Methods for Multi-Term Time-Fractional Reaction-Diffusion-Wave Equations. Applied Numerical Mathematics, 165, 56-82. https://doi.org/10.1016/j.apnum.2021.02.007
- 11. Liu, Y., Du, Y., Li, H., He, S. and Gao, W. (2015) Finite Difference/Finite Element Method for a Nonlinear Time-Fractional Fourth-Order Reaction-Diffusion Problem. Computers & Mathematics with Applications, 70, 573-591. https://doi.org/10.1016/j.camwa.2015.05.015
- 12. Liu, X.F. and Yang, X.Y. (2021) Mixed Finite Element Method for the Nonlinear Time-Fractional Stochastic Fourth-Order Reaction-Diffusion Equation. Computers & Mathematics with Applications, 84, 39-55. https://doi.org/10.1016/j.camwa.2020.12.004
- 13. Wang, Y.M. and Guo, B.Y. (2008) Fourth-Order Compact Finite Difference Method for Fourth-Order Nonlinear Elliptic Boundary Value Problems. Journal of Computational and Applied Mathematics, 221, 76-97. https://doi.org/10.1016/j.cam.2007.10.007
- 14. Meng, X., Shu, C.W. and Wu, B. (2012) Superconvergence of the Local Discontinuous Galerkin Method for Linear Fourth-Order Time-Dependent Problems in One Space Dimension. IMA Journal of Numerical Analysis, 32, 1294-1328. https://doi.org/10.1093/imanum/drr047
