Advances in Applied Mathematics
Vol.
13
No.
01
(
2024
), Article ID:
79632
,
10
pages
10.12677/AAM.2024.131026
基于Pythagorean Hodograph T-曲线的过渡 曲线的构造
杨雪,彭兴璇*
辽宁师范大学数学学院,辽宁 大连
收稿日期:2023年12月19日;录用日期:2024年1月13日;发布日期:2024年1月22日

摘要
本文基于平面三次T-Bézier曲线,定义了三次T-PH曲线,研究了T-PH曲线的代数和几何特征,进而利用三次T-PH曲线构造了两圆互不包含的情况下的C型过渡曲线,给出圆心距的取值范围,并证明了过渡曲线的唯一性。最后给出数值实例,验证了方法的可行性。
关键词
三次T-PH曲线,几何特征,过渡曲线

Construction of Transition Curve Based on Pythagorean Hodograph T-Curve
Xue Yang, Xingxuan Peng*
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Dec. 19th, 2023; accepted: Jan. 13th, 2024; published: Jan. 22nd, 2024

ABSTRACT
In this paper, we define the cubic T-PH curve and study the algebra and geometric characteristic of T-PH curve. In addition, a non-circle transition curve is constructed as a C-type transition curve using cubic T-PH curve, giving the value range of the center distance, and proving the uniqueness of transition curve. Finally, numerical examples are given to verify the feasibility of the method.
Keywords:Cubic T-PH Curve, Geometric Characteristic, Transition Curve

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Pythagorean-Hodograph (PH)曲线是Farouki [1] 提出的一种特殊的多项式参数曲线。由于PH曲线的曲率和等距曲线是有理形式的,因此被广泛应用在计算机辅助设计、机器人行走路线、数控机器加工等领域中。
到目前为止,基于一元多项式空间 中的PH曲线已经有了比较深入的研究。文献 [1] 给出了在边角分离的条件下,三次PH曲线的控制多边形的几何特征。但是有理式Bézier模型不能准确地表示超越曲线,因此,许多学者提出了三角空间和代数双曲混合空间。文献 [2] 定义了空间 上的C-Bézier曲线,并给出三次C-Bézier曲线成为PH曲线的充要条件;文献 [3] 以三次PH-C曲线的代数结构为基础,给出三次PH-C曲线的几何特征及构造方法。文献 [4] 定义了 上的AH-Bézier曲线,文献 [5] 在文献 [4] 的基础上,通过两种基底推导出三次PH-H曲线的充要条件,并给出PH-H曲线的几何构造方法;文献 [6] 定义了在三角多项式空间 上的T-Bézier曲线。目前三角多项式空间上的PH曲线尚无研究。
在曲线曲面的几何造型设计中,经常涉及到2条曲线间的光滑拼接,即过渡曲线的构造。由于过渡曲线要求在端点处满足几何连续性,并且曲线的曲率单调变化,因此文献 [7] 定义了用积分表示的Clothoid曲线,并将其用于公路铁路设计中。后来发现Clothoid曲线的表达式中含有Fresnel积分,计算复杂,许多学者开始对文献 [8] 提出了用三次Bézier曲线构造过渡曲线,但Bézier曲线的弧长和等距线不能表示为有理形式,在实际的几何设计中存在新的难题,为解决这一问题,文献 [9] [10] [11] 提出了利用五次PH曲线构造过渡曲线,五次PH曲线的内部不含奇点和拐点,其曲率单调,并且曲率和等距曲线是有理形式的,因此更适用于构造过渡曲线。为了使过渡曲线构造更为简单高效,文献 [12] 利用放缩法得到了类三次Bézier螺线,并构造了半径比例不受限制的两圆弧间S型和C型G2连续过渡曲线;文献 [13] [14] [15] 分别构造了C-Bézier螺线、H-Bézier螺线和T-Bézier螺线,并利用这些螺线作两圆之间的过渡曲线。为了避免求解复杂的非线性方程组,文献 [16] 采用次数较低的三次PH曲线构造相互包含的两圆弧间G2连续过渡曲线,文献 [17] 基于三次PH曲线,构造了两圆不相互包含的情况下的C型过渡曲线。
本文主要研究了T-PH曲线的代数和几何特征,并用来解决过渡曲线的构造问题。结构安排如下:首先,给出T-PH曲线的定义,并应用平面参数曲线的复数表示法,讨论T-PH曲线的代数结构和几何特征;其次,基于三次T-PH曲线来构造不互相包含的两圆之间的C型过渡曲线,并证明了过渡曲线的唯一性;最后,给出数值实例。
2. T-PH曲线
在三角多项式空间 中可以生成一类特殊曲线T-Bézier曲线。
定义1 [7] 给定平面上一组控制顶点 ,对于任意的 ,三次T-Bézier曲线表示为
(1)
其中 为T-Bézier曲线的基函数。其矩阵表示形式为
显然
则有
从而
(2)
其中
记 。
定义2平面T-Bézier曲线 ,若存在 使得其导数分量 满足 ,则称该曲线为Pythagorean Hodograph T-曲线,简称T-PH曲线。
3. 三次T-PH曲线的代数与几何特征
定理1 若参数曲线 满足:
其中 分别为实系数多项式,且不等于零,则 为PH曲线。
根据定义2和定理1,可以得到
定理2 式(1)中的三次T-Bézier曲线 是PH曲线的充要条件是存在实数 ,使得其控制顶点满足如下关系式
(3)
其中
(4)
证明:令
由T-Bézier曲线的基函数得
三次T-Bézier曲线的导数可写为
因此得到T-PH曲线的控制顶点:
其中 需满足
对上式进行整理即可得到式(3),从而得到了三次T-Bézier曲线成为T-PH曲线的充要条件。
下面将用一个例子来说明定理2,用定理中的充要条件给定参数取值,计算出曲线的控制顶点,并根据T-Bézier曲线的表达式构造出两条三次T-PH曲线。
例1给定 ,则由式(3)可得三次T-PH曲线的控制顶点为:
得到的三次T-PH曲线及其控制多边形如图1所示。
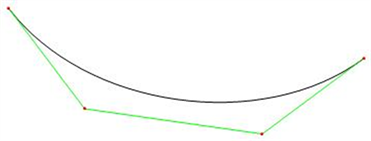
Figure 1. Cubic T-PH curve and control polygon
图1. 三次T-PH曲线及控制多边形
Farouki已经得出三次多项式PH曲线具有简单的几何性质,利用这个性质可以对三次多项式PH曲线进行判别和构造,接下来将证明三次T-PH曲线也具有类似的几何性质。
定理3 若 为三次T-Bézier曲线 的控制顶点, 为控制多边形的两个内角, 为控制多边形的三条边长,则 是T-PH曲线当且仅当
(5)
证明:由定理2可知,若一条三次T-Bézier曲线为T-PH曲线,则存在实数 使得式(3)、(4)成立。记 为 的辐角,可得
(6)
(7)
(8)
分别计算 和 的实部和虚部,得到
其中
由式(4)化简得到
其中
由式(4)化简得到
从而可得
(9)
因为 为控制多边形的内角,即 ,所以由式(9)可知式(5)成立。
反之,若对于给定的三次T-PH曲线,其控制多边形满足式(5),则假定 为待定系数,使得式(6)~式(8)成立。若式(6)、式(7)成立,则式(8)也成立。因此分别考虑复方程(6)的实部和虚部,通过求解线性方程组得到
进一步,将 作为已知量,分别考虑复方程(7)的实部和虚部,通过求解线性方程组得到
综上,得到使定理3成立的4个实数 ,因此,该曲线是一条三次T-PH曲线。证毕。
4. 三次T-PH过渡曲线的构造
平面参数曲线的曲率表达式为:
设三次T-PH曲线的控制多边形初始端点为P0,末端点为P3,以P0为原点建立直角坐标系,由P0处的曲率可得到以C0为圆心,r0为半径的圆Ω0,由P3的曲率可得到以C1为圆心,r1为半径的圆Ω1,如图2所示。
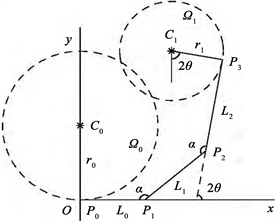
Figure 2. Circle of curvature [17]
图2. 曲率圆 [17]
由图2得三次T-PH曲线的控制顶点为:
(10)
将式(10)代入式(1)中,得到 的参数表达式为:
其中
(11)
(12)
对式(11)、式(12)求导,得到T-PH曲线导数的模长为
则曲率表达式为
(13)
将 代入式(13)分别得到初始端点和末端点的曲率 和
因为 ,所以 和 同号,因此当两个圆互不包含时,所构造的三次PH过渡曲线是C型的。
设 、 为是末端点的曲率半径, 令 则 。
定理4 当 时,即两圆不互相包含时,若
则过渡曲线是一个C型过渡曲线。
证明:对式(13)求导,得到三次T-PH曲线的曲率导数为
(14)
则
得
由于 , ,故当 时,
即 ,此时,三次T-PH曲线的内部含有尽量少的曲率极值点,且所构造的三次T-PH曲线是C型G2连续的过渡曲线。
下面讨论三次T-PH过渡曲线的唯一性。
定理5 设给定端点的曲率为 和 ,相应的曲率半径为 和 ,令 ,若
且
其中
若所构造的三次T-PH过渡曲线符合上述条件,则该曲线是唯一的。
证明:由图2知,两圆的圆心分别为 , ,则圆心距 ,设圆心距长度为r,则 。
由始末端点曲率 和 及 可得
(15)
(16)
由 ,得
(17)
构造函数 ,令 ,则 。将式(10)中T-PH曲线的控制顶点代入 中,得到关于h的方程
因为 ,考虑 在 上的情况:
由零点定理, 有解的充分条件为 。
由 得 ,因为 ,所以 ,从而 。
经计算,当 时, 成立,此时 在 有根。

Figure 3. Cubic T-PH transition curves between two circles that do not contain each other
图3. 互不包含的两圆之间的三次T-PH过渡曲线
接下来讨论h的唯一性:
是关于h的二次多项式,且开口向下,另外 , ,所以 是增函数,又 , , ,因此 在 有唯一的根。
5. 数值例子
取 , ,由 ,取 ,计算得出过渡曲线两端点的曲率圆的圆心距范围为 ,取 ,解得 ,生成的三次T-PH过渡曲线如图3所示。
6. 总结
本文基于三角多项式空间,给出了三次T-Bézier曲线成为T-PH曲线的几何特征。本文研究的另一个问题,即利用三次T-PH曲线的几何特征,构造了互不包含的两圆之间的三次T-PH过渡曲线,由于过渡曲线次数较低,所以计算方便,易在CAD中实现。
文章引用
杨 雪,彭兴璇. 基于Pythagorean Hodograph T-曲线的过渡曲线的构造
Construction of Transition Curve Based on Pythagorean Hodograph T-Curve[J]. 应用数学进展, 2024, 13(01): 234-243. https://doi.org/10.12677/AAM.2024.131026
参考文献
- 1. Farouki, R.T. and Sakkalis, T. (1990) Pythagorean Hodographs. IBM Journal of Research and Development, 34, 736-752. https://doi.org/10.1147/rd.345.0736
- 2. Chen, Q. and Wang, G. (2003) A Class of Bézier-Like Curves. Computer Aided Geometric Design, 20, 29-39. https://doi.org/10.1016/S0167-8396(03)00003-7
- 3. 李毓君, 方林聪. Pythagorean Hodograph C-曲线的几何构造方法[J]. 数学学报(中文版), 2023, 66(2): 353-362.
- 4. Li, Y.J. and Wang, G.Z. (2005) Two Kinds of B-Basis of the Algebraic Hyperbolic Space. Journal of Zhejiang University—Science, 6, 750-759. https://doi.org/10.1631/jzus.2005.A0750
- 5. 廖莲星. 三次Pythagorean-hodograph曲线的造型研究[D]: [硕士学位论文]. 镇江: 江苏大学, 2023.
- 6. 苏本跃, 黄有度. 一类Bézier型的三角多项式曲线[J]. 高等学校计算数学学报, 2005(3): 14-20.
- 7. Meek, D.S. and Walton, D.J. (1989) The Use of Cornu Spirals in Drawing Planar Curves of Controlled Curvature. Journal of Computational and Applied Mathematics, 25, 69-78. https://doi.org/10.1016/0377-0427(89)90076-9
- 8. Walton, D.J. and Meek, D.S. (1998) Planar G2 Curve Design with Spiral Segments. Computer-Aided Design, 30, 529-538. https://doi.org/10.1016/S0010-4485(98)00007-4
- 9. Walton, D.J. and Meek D.S. (1999) A Pythagorean Hodo-graph Quintic Spiral. Computer-Aided Design, 28, 943-950. https://doi.org/10.1016/0010-4485(96)00030-9
- 10. Walton, D.J. and Meek D.S. (1998) G2 Curves Composed of Planar Cubic and Pythagorean Hodograph Quintic Spirals. Computer Aided Geometric Design, 15, 547-566. https://doi.org/10.1016/S0167-8396(97)00028-9
- 11. Walton, D.J. and Meek, D.S. (2007) G2 Curve Design with a Pair of Pythagorean Hodograph Quintic Spirals. Computer Aided Geometric Design, 24, 267-285. https://doi.org/10.1016/j.cagd.2007.03.003
- 12. 高晖, 寿华好, 缪永伟, 等. 3个控制顶点的类三次Bézier螺线[J]. 中国图象图形学报, 2014, 19(11): 1677-1683.
- 13. 蔡华辉, 王国瑾, 三次C-Bézier螺线的构造及其在道路设计中的应用[J]. 浙江大学学报(工学版), 2010, 44(1): 68-74.
- 14. 蔡华辉, 柳炳祥, 程燕. 三次平面H-Bézier螺线[J]. 图形学报, 2014, 35(3): 374-378.
- 15. 王子洋. 基于类Bézier曲线的过渡曲线的研究[D]: [硕士学位论文]. 合肥: 合肥工业大学, 2018.
- 16. 郑志浩, 汪国昭. 三次PH曲线的曲率单调性及过渡曲线构造[J]. 计算机辅助设计与图形学学报, 2014, 26(8): 1219-1224.
- 17. 刘莹莹, 王旭辉. 平面三次PH过渡曲线的构造[J]. 合肥工业大学学报(自然科学版), 2016, 39(9): 1288-1291.
NOTES
*通讯作者。