Advances in Applied Mathematics
Vol.
11
No.
01
(
2022
), Article ID:
48076
,
5
pages
10.12677/AAM.2022.111027
一类空间分数阶Burgers方程 守恒型差分方法
胡婷,傅毛里
长沙理工大学数学与统计学院,湖南 长沙
收稿日期:2021年12月17日;录用日期:2022年1月6日;发布日期:2022年1月19日

摘要
本文采用守恒型差分方法求解一类空间分数阶Buegers方程,其中时间方向和空间方向分别采用Crank-Nicolson格式和有限差分法离散。实验结果表明,该方法在时间和空间上的收敛速度都为二阶。
关键词
空间分数阶Burgers方程,守恒型差分方法,Crank-Nicolson格式

A Conservative Difference Method for a Space-Fractional Burgers Equation
Ting Hu, Maoli Fu
School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha Hunan
Received: Dec. 17th, 2021; accepted: Jan. 6th, 2022; published: Jan. 19th, 2022

ABSTRACT
This paper develops a conservative discretization for a space-fractional Burgers equation, in which the temporal Crank-Nicolson scheme and spacial finite difference method are used. Numerical test shows that the convergence of this method is of order 2 in time and space.
Keywords:Space-Fractional Burgers Equations, Conservative Difference Method, Crank-Nicolson Scheme

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 介绍
近年来,由于分数阶导数的记忆性质,使分数阶微分方程对自然物理和动力系统过程的建模更加精确,因而在工程、流体力学、物理、化学、金融等领域的应用越来越广泛。对于分数阶微分方程的求解,虽然有一些方法可以得到它的解析解,但大多数情况下,这类方程的解析解难以求解,因此求分数阶微分方程的数值解尤为重要。
本文考虑下述空间分数阶Burgers方程
,,, (1.1)
满足初边值条件
,, (1.2)
其中 ,, 为给定函数, 阶Caputo分数阶导数
. (1.3)
方程(1.1)可模拟充气管道中弱非线性声波的单向传播,其中分数阶导数反映了声波在通过充气管道边界层时所产生的壁摩擦积累效应 [1]。对于方程(1.1),Sugimoto [1] 和Wu等 [2] 分别使用有限差分法和谱方法对此类方程进行了求解;杨和马 [3] 使用了Chebyshev配置法求解该方程,并给出了稳定性分析及误差估计。
本文构造一种守恒型差分法来求解空间分数阶Burgers方程的数值解,内容组织如下,第二节,引入守恒型差分法;第三节,给出数值算例验证该方法的有效性;第四节,对本文进行总结。
2. Burgers方程的离散格式
定义网格节点 ,, ; ,其中 ,,N,L为两个正整数。令u在 处的精确值和近似值分别记为 和 ,并记 。
我们假定解u是光滑函数,u2满足Lipschitz条件
,
在算法中取h满足
, (2.1)
其中 , 是Riemann zeta函数。
将在点 处方程(1.1)写成如下形式
. (2.2)
对空间导数使用中心差商近似
, (2.3)
, (2.4)
对Caputo分数阶导数,采用一种二阶近似方法 [4]
, (2.5)
其中 ,直接可以验证
,. (2.6)
将(2.3)~(2.5)代入(2.2),时间方向使用Crank-Nicolson格式近似,得到
(2.7)
其中 为截断误差,
(2.8)
, (2.9)
从而得到全离散格式
, (2.10)
其中 , 由(2.8)和(2.9)定义得到。当 , 表示在 点的通量,算法具有守恒结构 [5],这种守恒性可以帮助捕捉解的奇异位置。
3. 数值实验
本节提供两个算例,分别用于测试算法的收敛阶和解的奇异位置捕捉能力(表1,表2)。
例3.1 考虑右端带有原项
,(3.1)
的方程(1.1),初始条件为 ,,,,问题的解为 。
下表中 表示在 处数值解与精确解的误差,结果表明算法时间和空间方向2阶收敛。
Table 1. Error and order of convergence in spatial direction when L = 10,000
表1. 当L = 10,000时,空间方向上的误差及收敛阶
Table 2. Error and order of convergence in spatial direction when N = 8000
表2. 当N = 8000时,时间方向上的误差及收敛阶
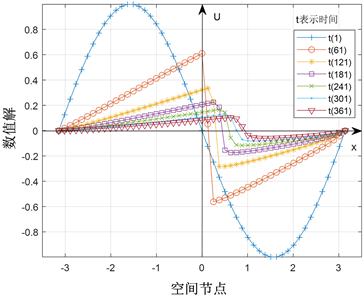
Figure 1. Numerical solutions with singular solutions, (left) and (right)
图1. 带有“奇异解”情形数值解, (左)和 (右)
例3.2 取 ,,,,,, 或 。
图1中横坐标x表示空间节点,纵坐标U表示数值解,每种线型表示某一特定时刻数值解随空间坐标的变化情况。该图结果表明,我们的算法在求解“奇异解”问题时具有很好的效果。
4. 结论
本文研究了一类空间分数阶Burgers方程,当方程中的 取值较小时,该方程具有一定的奇异性,采用守恒型差分方法求解了此类带有奇异解的方程,并验证了该数值方法的有效性,得到时间和空间方向上的收敛速度都为2阶。
文章引用
胡 婷,傅毛里. 一类空间分数阶Burgers方程守恒型差分方法
A Conservative Difference Method for a Space-Fractional Burgers Equation[J]. 应用数学进展, 2022, 11(01): 219-223. https://doi.org/10.12677/AAM.2022.111027
参考文献
- 1. Sugimoto, N. (1991) Burgers Equation with a Fractional Derivative; Hereditary Effects on Nonlinear Acoustic Waves. Journal of Fluid Mechanics, 225, 631-653. https://doi.org/10.1017/S0022112091002203
- 2. Wu, Q. and Zeng, X. (2020) Jacobi Collocation Methods for Solving Generalized Space-Fractional Burgers Equations. Communications on Applied Mathematics and Computation, 2, 305-318. https://doi.org/10.1007/s42967-019-00053-6
- 3. 杨宇博, 马和平. 广义空间分数Burgers方程的Legendre Galerkin-Chebyshev配置方法逼近[J]. 数值计算与计算机应用, 2017, 38(3): 236-244.
- 4. Dimitrov, Y. (2015) A Second Order Approximation for Caputo Fractional Derivative. https://arxiv.org/abs/1502.00719
- 5. Hesthaven, J.S. (2017) Chapter 4: From Continuous to Discrete. In: Numerical Methods for Conservation Laws. https://doi.org/10.1137/1.9781611975109.ch4
