Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21534,8
pages
10.12677/AAM.2017.64076
Optimization of Preconditioner in Conjugate Gradient Method
Cunzhu Guo
School of Mathematics & Information, Longnan Teacher’s College, Longnan Gansu

Received: Jul. 9th, 2017; accepted: Jul. 24th, 2017; published: Jul. 27th, 2017

ABSTRACT
For decreasing the conditional number of the coefficient matrix in solving the linear equations with conjugate gradient methods and accelerating the convergence, it is common to use preconditioned methods to find the equivalent equations, whose conditional numbers are smaller. It is required that the preconditioners should be as close as possible to the original coefficient matrix and their inverse matrices can be easily computed. Starting from diagonal preconditioners, we first compute the eigenvalue decomposition of the coefficient matrix, and obtain the optimal preconditioner. However, it is of high computational complexity to do the eigenvalue decomposition. In this paper, we introduce three p-norm preconditioners to approximate the optimal preconditioner. Comparing with the existing preconditioners, the experimental results show that the proposed three diagonal p-norm preconditioners converge much faster, which demonstrates the advantages of the proposed family of preconditioners.
Keywords:Preconditioner, Condition Number, Eigenvalue Decomposition, p-Norm Preconditioner
共轭梯度法中预条件子的优化
郭存柱
陇南师专数信学院,甘肃 陇南
收稿日期:2017年7月9日;录用日期:2017年7月24日;发布日期:2017年7月27日

摘 要
为了降低方程组求解中共轭梯度法系数矩阵的条件数,提高收敛速度,常用预处理方法将原方程进行等价转化,同时预条件子既要接近原系数矩阵,又要容易求其逆矩阵。本文从寻求对角预条件子出发,用矩阵的特征值分解方法解出了预处理后系数矩阵特征值矩阵的显式表达,得到对角预条件子矩阵的最优选择,并予以证明。给出了三个p-范数预条件子,将之与常用的预条件子进行对比,实例检验表明三个p-范数预条件子的作用更优越,且使算法收敛更快。
关键词 :预条件子,条件数,特征值分解,p-范数预条件子

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
使用求解方程组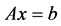 (其中A为n阶对称正定矩阵,x为
(其中A为n阶对称正定矩阵,x为 未知向量,b为
未知向量,b为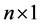 已知向量),理论上可以在n步之内得到精确解。但由于机器的舍入误差,可能需迭代超过n步才能达到所需精度的解。尤其当A的条件数很大时,迭代求解过程总体收敛会很慢,因之这一优越的方法在一段时间曾被搁置。直到引入预条件处理方法(用
已知向量),理论上可以在n步之内得到精确解。但由于机器的舍入误差,可能需迭代超过n步才能达到所需精度的解。尤其当A的条件数很大时,迭代求解过程总体收敛会很慢,因之这一优越的方法在一段时间曾被搁置。直到引入预条件处理方法(用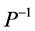 乘以原方程组,得到同解方程组
乘以原方程组,得到同解方程组 ),来降低系数矩阵的条件数(
),来降低系数矩阵的条件数(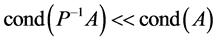 ),提高了迭代速度和稳定性,才使共轭梯度法在工程、微分方程数值求解和最优化等领域得到广泛应用。
),提高了迭代速度和稳定性,才使共轭梯度法在工程、微分方程数值求解和最优化等领域得到广泛应用。
2. 已有成果 [1]
预条件子(亦称条件预优矩阵)P的选取应接近A,且容易求逆,正对角阵为首选。此前共轭梯度法常用的预条件子有以下三种。
2.1. Jacobi预条件子
取 ,其中D为A的对角阵。
,其中D为A的对角阵。
2.2. Gauss-Seidel预条件子
取 ,其中A被分解为
,其中A被分解为 ,D、L、U为对角阵、下三角阵、上三角阵,
,D、L、U为对角阵、下三角阵、上三角阵,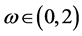 。当
。当 时即为Gauss-Seidel预条件子。
时即为Gauss-Seidel预条件子。
2.3. 不完全Cholesky分解预条件子 [2]
由Meijerink J.A.和Van der vorst A.1977年提出 [3] 。将A分解成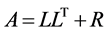 ,其中L为下三角阵,且与A有一样的稀疏性(当
,其中L为下三角阵,且与A有一样的稀疏性(当 时,有
时,有 )。
)。
取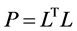 ,或
,或 。
。
3. 目标问题
已知矩阵A,求矩阵P,使得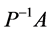 的条件数最小,即
的条件数最小,即
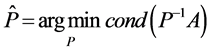
4. 概念、定理与符号
4.1. 定义(谱条件数)
设正定矩阵A的特征值分别为 ,
,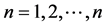 ,则A的谱条件数为
,则A的谱条件数为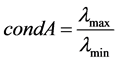 。
。
4.2. 矩阵的谱分解定理
设n阶矩阵A的特征值分别为 ,相应的特征向量为
,相应的特征向量为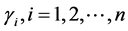 为标准正交向量组,即
为标准正交向量组,即

记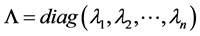 ,
,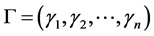 ,其中,
,其中,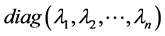 表示对角元素分别为
表示对角元素分别为
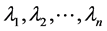 的对角矩阵,则A可分解为
的对角矩阵,则A可分解为
 (1)
(1)
4.3.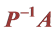 的谱分解
的谱分解
设 的特征值分别为
的特征值分别为 ,相应的特征向量为
,相应的特征向量为 为标准正交向量组,即
为标准正交向量组,即
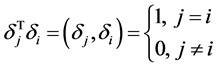
记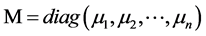 ,
,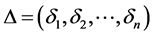 ,
,
由矩阵的谱分解定理
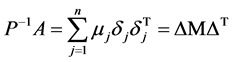 (2)
(2)
5. 求解
首先想到的是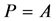 ,因
,因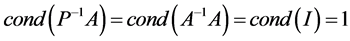 ,条件数最小。但求
,条件数最小。但求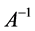 和解方程组是同一问题,当A的条件数很大时误差会很大,且其时间复杂度为
和解方程组是同一问题,当A的条件数很大时误差会很大,且其时间复杂度为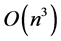 .
.
5.1. 最优预条件子
将(1)两边乘以 得
得
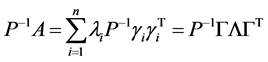 (3)
(3)
由(2)、(3)得
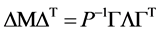
解得
 (4)
(4)
 的条件数最小化问题化为
的条件数最小化问题化为
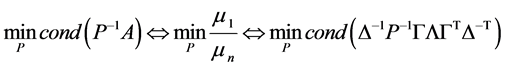 (5)
(5)
由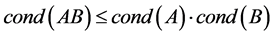 ,且
,且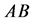 与
与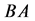 有相同的非零特征值 [4] ,
有相同的非零特征值 [4] ,
从而, ,
,
所以 ,
,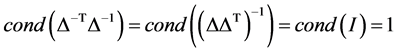
(5)化为
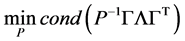 (6)
(6)
设 ,
,
由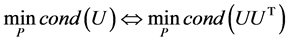 , (6)等价于
, (6)等价于

 (7)
(7)
其中 ,要使得(7)条件数最小化为1,只需
,要使得(7)条件数最小化为1,只需
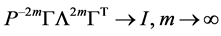 (8)
(8)
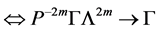
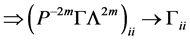
所以
 (9)
(9)
否则,用反证法。
为简单起见,不妨设 ,
,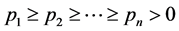 ,
,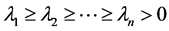 ,
, ,
, ,则
,则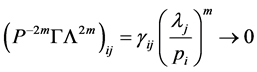 ,(
,( ),
), ,
,

若 ,
,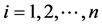
则 ,(
,( ),
),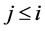 ,
,

这与(8)矛盾,如此,就证明了(9)成立。
因此,对角预条件子P的最优选择是A的特征值矩阵 ,此时,
,此时,

为最小。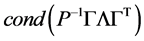 趋向于最小值1。
趋向于最小值1。
5.2. 最优预条件子的近似替代
在数值计算中,当A的特征值非常接近于0时,由于机器的舍入误差容限,计算机将其按0对待,导致无法求逆。因而,寻找可逆矩阵P近似替代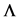 。
。
5.2.1. 列范数预条件子
取由A的各列的p-范数为对角元素的矩阵作为预条件子P,即
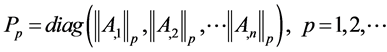
其中,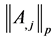 表示A的第j列的p-范数,
表示A的第j列的p-范数,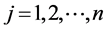 。
。
分别取 ,可得以下三种不同列范数预条件子。
,可得以下三种不同列范数预条件子。
5.2.2. 列绝对和(1-范数)预条件子
取
5.2.3. 列Euclid(2-范数)预条件子
取
5.2.4. 列最大模(¥-范数)预条件子
取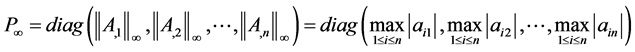
当A为正定对角矩阵时,三个p-范数预条件子都等于A。
6. 实例检验
使用Matlab的预条件子共轭梯度函数pcg和双线性共轭梯度函数bicg。
实例1. 当A为13阶Hilbert矩阵,x = ones(n) (n个1); b = A*x; cond(A) = 8.3042 × 1019,用1-范数预条件子1-步达精确值、∞-范数预条件子13步相对误差小于10−16、2-范数预条件子17步相对误差小于10−16,其次是Jacobi、Gauss-Seidel预条件子和不用预条件子,用不完全Cholesky预条件子表现最差。如图1。
实例2. 当n = 1000; A = diag((1:n).^2) + diag((1:n-20).^(1/2),20) + diag((1:n − 20).^(1/2),−20); x, b同例1(下同); cond(A) = 1.0023 × 106,用1-范数预条件子2步达精确值、Gauss-Seidel预条件子6步相对误差小于10−16,2-范数、∞-范数、Jacobi预条件子17步相对误差小于10−16,其次是不完全Cholesky预条件子,不用预条件子收敛非常慢,如图2。
实例3. 当n = 33; A = log([5:n + 4]')*([1:n].^2); cond(A) = 1.2857 × 1020,用1-范数、∞-范数预条件子迭代1步达精确值,2-范数预条件子迭代1步相对误差小于10−16, 无法进行Cholesky分解,如图3。
实例4. 当n = 3000; A = diag(1./(3:n + 2)) + diag(1./(n − 1:1),1) + diag(1./(n − 1:1),−1); cond(A) = 1.0007 × 103,全部预条件子表现都优越,且用1-范数、2-范数、∞-范数预条件子表现最好,1步达到精确值,如图4。
实例5. 当n = 2000; A = magic(n); A非正定, cond(A) = 8.5285 × 1020,其它方法无法进行,用1-范数1步迭代达精确值,不用预条件子迭代10步相对误差小于10−15,如图5。
实例6. 当n = 1000; A = diag((1:n)) + diag(sin(1:n − 3),3) + diag(sin(1:n − 3), −3) + diag(sin(1:n − 20),20) + diag(sin(1:n − 20),−20) + diag(cos(1:n − 100), 100) + diag(cos(1:n − 100),−100); cond(A) = 1.3568 × 103,Gauss-Seidel预条件子表现优越,迭代16步误差即小于10−18,其次是不完全2-范数、∞-范数、Jacobi、1-范数、Cholesky预条件子,不用预条件子收敛非常慢,如图6。

Figure 1. Figure of instance 1
图1. 实例1图

Figure 2. Figure of instance 2
图2. 实例2图

Figure 3. Figure of instance 3
图3. 实例3图
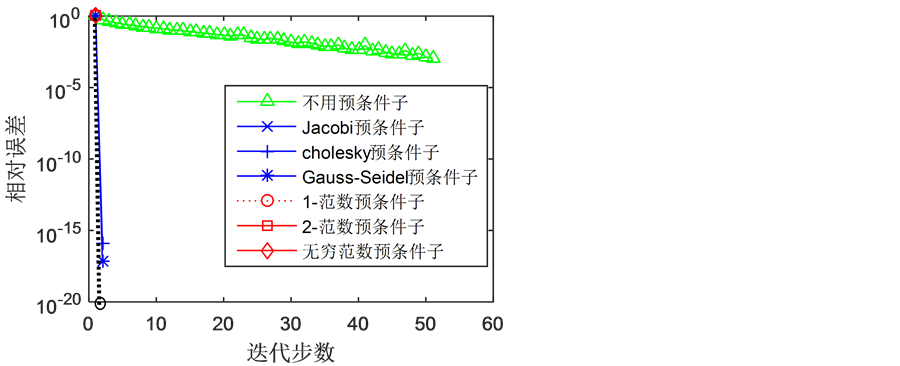
Figure 4. Figure of instance 4
图4. 实例4图

Figure 5. Figure of instance 5
图5. 实例5图

Figure 6. Figure of instance 6
图6. 实例6图
7. 算法复杂度
共轭梯度法的算法复杂度取决于矩阵与向量乘积的次数,如恰当设计程序使每步迭代只有一次矩阵与向量的乘法,在矩阵稀疏时,时间复杂度为 。而使用预条件子的共轭梯度法大大降低了复杂度,
。而使用预条件子的共轭梯度法大大降低了复杂度,
节省了计算的时间成本,提高了运算速度和精度。其中用列范数预条件子方法迭代次数远远小于矩阵阶数n。考虑到两矩阵乘积、矩阵与向量乘积的复杂度,对稀疏矩阵而言,列Euclid范数、Gauss-Seidel范
数、不完全Cholesky分解预条件子的复杂度都是 ,而列最大模、绝对和预条件子复杂度为
,而列最大模、绝对和预条件子复杂度为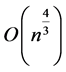 。
。
文章引用
郭存柱. 共轭梯度法中预条件子的优化
Optimization of Preconditioner in Conjugate Gradient Method[J]. 应用数学进展, 2017, 06(04): 651-658. http://dx.doi.org/10.12677/AAM.2017.64076
参考文献 (References)
- 1. Sauer Timothy. 数值分析[M]. 裴玉茹, 马赓宇, 译. 北京: 机械工业出版社, 2015.
- 2. 林成森. 数值计算方法[M]. 第2版. 北京: 科学出版社, 2005.
- 3. Meijerink, J.V. and Van der Vorst, H.A. (1977) An Iterative Solution Method for Linear Systems of Which the Coefficient Matrix Is a Symmetric M-Matrix. Mathematics of Computation, 31, 148-162.
- 4. Horn R.A. and Johnson, C.R. (2015) Matrix Analysis. 2nd Edition, Cambridge University Press, London.