Advances in Applied Mathematics
Vol.
12
No.
06
(
2023
), Article ID:
67666
,
8
pages
10.12677/AAM.2023.126291
用动力系统方法研究一类时间分数阶扩散方程的精确解
黎超玲
重庆师范大学数学科学学院,重庆
收稿日期:2023年5月25日;录用日期:2023年6月19日;发布日期:2023年6月27日

摘要
随着时代的发展,分数阶微分模型的应用越来越广泛,故对其研究非常有必要。本文在Riemann-Liouville分数阶导数的定义下利用半固定式变量分离法与动力系统理论相结合的方法,研究了一类时间分数阶扩散方程的精确解,获得了方程的一系列精确解,通过解的坐标演化图直观地展示了在不同参数条件下的扩散现象。
关键词
时间分数阶扩散方程,Riemann-Liouville分数阶导数,半固定式变量分离法,动力系统方法,精确解

Exact Solutions of a Class of Time-Fractional Diffusion Equation by Dynamic System Method
Chaoling Li
School of Mathematical Sciences, Chongqing Normal University, Chongqing
Received: May 25th, 2023; accepted: Jun. 19th, 2023; published: Jun. 27th, 2023

ABSTRACT
With the development of the times, the application of fractional differential model is more and more extensive, so it is very necessary to study it. In this paper, under the definition of Riemann-Liouville fractional derivative, the exact solution of a class of time fractional diffusion equations is studied by combining semi-fixed variable separation method with dynamic system theory, and a series of exact solutions of the equations are obtained. The diffusion phenomenon under different parameter conditions is intuitively displayed through the coordinate evolution diagram of the solutions.
Keywords:Time Fractional Diffusion Equation, Riemann-Liouville Fractional Derivative, Semi-Fixed Variable Separation Method, Dynamical System Method, Exact Solutions

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分数阶微积分和整数阶微积分都起源于同一个时代,即Leibniz时代。但由于过去分数阶微积分缺乏应用背景,所以分数阶微积分比整数阶微积分发展得困难和缓慢。几代数学家们通过300多年的共同努力,分数阶微积分理论终于被建立起来了,并且人们还发现可以用分数阶微分模型来描述,如反常扩散现象、记忆现象、粘弹性现象等问题,因此,自上个世纪60年代以来分数阶微积分得到了快速的发展。如今,分数阶微积分已经被广泛地应用到了数学力学、信号处理、生物学和化学等自然科学和工程领域,而且还出现了关于求解分数阶微分方程的一系列求解方法,如:Adomian分解法 [1] [2] ,同伦分析法 [3] [4] ,不变分析法 [5] [6] ,分式变分迭代法 [7] [8] [9] ,不变子空间法 [10] [11] [12] ,分数阶复变换法 [13] [14] [15] 和分离变量法 [16] [17] [18] 等等。尽管用上面一系列的方法,可以求出分数阶微分方程的一部分精确解,但对于更复杂的分数阶微分方程而言,仍很难获得其精确的解析表达式。
在本文中,我们将在文献 [12] 的基础上,利用Rui在文献 [19] [20] 中提出的半固定式变量分离法与动力系统理论相结合的方法,研究了下列形式的时间分数阶扩散方程:
(1)
其中 为任意非零常数, 为Riemann-Liouville型分数阶微分算子。
2. 扩散方程的约化及相应的非线性平面动力系统
在本节中,对于方程(1),我们将采用半固定式变量分离法,将其约化成一个非线性平面动力系统,然后再讨论这个系统的相空间结构以及相应的动力学性质。
设方程(1)的解为
(2)
其中 为x的待定函数, 为待定常数且 ,把(2)代入(1)得:
(3)
其中 。根据齐次平衡原理,令方程(3)中含有t项的幂指数相等,即有:
(4)
由(4)解得:
(5)
显然幂指数 满足幂函数对Riemann-Liouville求导的条件,当 时,方程(3)中的 变为 ,将(5)代入(3)中并分约去时间项 得到:
(6)
令 ,则方程(6)可简化为下列奇异的平面动力系统:
(7)
当 时,我们发现 没有任何意义,此时系统(6)与方程(7)不等价。为了得到与方程(6)完全等价的系统,我们做下列尺度变换:
(8)
其中 是一个参数。通过变换式(8)可以将奇异系统(7)简化为以下规则的平面系统:
(9)
无论函数v如何变化,此时方程(6)和系统(9)是等价的。显然,系统(7)和(9)具有相同的首次积分,为:
(10)
这里h是一个积分常数。为了便于后面的讨论,我们将方程(10)改写成如下的形式:
(11)
利用平面系统(9)和方程(11),验证易得 ,因此判断系统(9)不是一个哈密顿系统。令 , ,可得到系统(9)的平衡点为 。把平衡点代入(11)中,得:
(12)
记 , 。可得系统(9)的雅可比矩阵和雅可比行列式:
(13)
(14)
(15)
由平面动力系统的相关知识可知,系统中平衡点的类型决定了平面相图中轨道的走向与分布,从而决定了方程(6)的不同类型的解和动力学行为,同时也确定了原方程的解的类型和动力学性质。
根据平衡点的特征,我们下面给出当 和 时平面系统(9)的相图1和相图2,并对方程(6)的解进行讨论。为了方便查看图形,在下面的图形中,用黑色线条标记 定义的轨道,用红色线条标记 定义的轨道,用蓝色(或绿色)线条标记 定义的轨道。
 (a)
(b)
(a)
(b)
Figure 1. Plane phase diagram of system (9) when
图1. 当 时系统(9)的平面相图
 (a)
(b)
(a)
(b)
Figure 2. Plane phase diagram of system (9) when
图2. 当 时系统(9)的平面相图
3. 扩散方程的各种精确解
根据上一节的分析,在本节中我们将通过沿着相图中轨道积分的方法来获得扩散方程的精确解。
当 时,方程(10)可化为:
(16)
取原点为初值点,将(16)式代入(7)的第一个方程后沿轨道进行积分,可得到:
(17)
完成(17)式的积分,可得常微分方程(6)的两个解:
(18)
(19)
将(18)、(19)和(5)式代入(2)式中,可得到方程(1)的两个精确解:
(20)
(21)
其中(20)和(21)是一个随时间增加而衰减的解,显然当 时, 。
当 且 时,系统(9)有多个用红色标记的轨道,如图1(a)和图1(b)所示。在这种情形下,方程(10)可简化为:
(22)
以 为初值条件,同理可得:
(23)
求解(23),我们得到常微分方程(6)的两个解如下:
(24)
(25)
将上述两个有界解和(5)代入(2)中,我们可得到方程(1)的两个具有周期性质的解,为:
(26)
(27)
当 且 时,方程(10)可简化为:
(28)
将(28)代入(7)的第一个方程进行积分得:
(29)
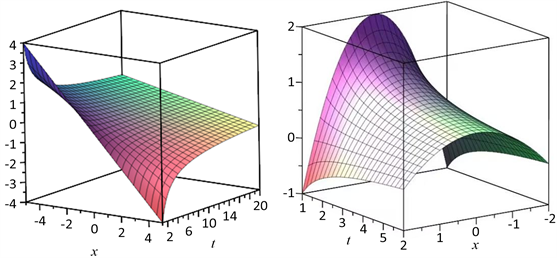 (a) 解(20)的三维图形(b) 解(31)的三维图形
(a) 解(20)的三维图形(b) 解(31)的三维图形
Figure 3. Three-dimensional coordinate graphs of solutions (20) and (31)
图3. 解(20)和(31)的三维坐标图形
对(29)进行积分,可得到常微分方程(6)的解如下:
(30)
将(30)、(5)代入(2)中,可得到方程(1)有界解如下:
(31)
为了能够直观地展示上述解的动态特性,作为例子,分别绘制了解(20)和(31)的三维坐标图形,见图3(a)和图3(b)。从图3可以看出,扩散现象是随着时间的增加而衰减的。
4. 结论与展望
本文在以Riemann-Liouville型分数阶导数的定义下,通过半固定式变量分离与动力系统相结合的新方法研究了一类时间分数阶扩散方程的精确解,一方面扩展和修改了文献中的方法;另一方面采用的变量分离法也与经典的变量分离法有所不同,本文的变量分离法是把时间部分的函数固定成一些特殊的函数,如幂函数等。
虽然本文中时间分数阶微分方程的解是在新的方法下获得的,但是在完成论文的过程中也遇到一些困难,仍有很多问题需深入探讨。如:
1) 本文中方程的一系列精确解是在一些特定的参数条件下得到的,那么在一般的参数条件下能否求出方程的精确解呢?也是一个值得继续关注的问题。
2) 本文对于时间分数阶偏微分方程的精确解,只求出了其时间变量部分为幂函数形式的精确解,关于其它特殊函数形式的精确解还有待研究。
文章引用
黎超玲. 用动力系统方法研究一类时间分数阶扩散方程的精确解
Exact Solutions of a Class of Time-Fractional Diffusion Equation by Dynamic System Method[J]. 应用数学进展, 2023, 12(06): 2896-2903. https://doi.org/10.12677/AAM.2023.126291
参考文献
- 1. Daftardar-Gejji, V. and Jafari, H. (2005) Adomian Decomposition: A Tool for Solving a System of Fractional Differen-tial Equations. Journal of Mathematical Analysis and Applications, 301, 508-518. https://doi.org/10.1016/j.jmaa.2004.07.039
- 2. Bakkyaraj, T. and Sahadevan, R. (2014) An Approximate Solution to Some Classes of Fractional Nonlinear Partial Differential-Difference Equation Using Adomian Decomposition Method. Journal of Fractional Calculus and Applications, 5, 37-52.
- 3. Bakkyaraj, T. and Sahadevan, R. (2016) Approximate Analytical Solution of Two Coupled Time Fractional Nonlinear Schrodinger Equations. International Journal of Applied and Computational Mathematics, 2, 113-135. https://doi.org/10.1007/s40819-015-0049-3
- 4. Bakkyaraj, T. and Sahadevan, R. (2014) On Solutions of Two Coupled Fractional Time Derivative Hirota Equations. Nonlinear Dynamics, 77, 1309-1322. https://doi.org/10.1007/s11071-014-1380-7
- 5. Sahadevan, R. and Bakkyaraj, T. (2012) Invariant Analysis of Time Fractional Generalized Burgers and Korteweg-de Vries Equations. Journal of Mathematical Analysis and Applica-tions, 393, 341-347. https://doi.org/10.1016/j.jmaa.2012.04.006
- 6. Bakkyaraj, T. and Sahadevan, R. (2015) Invariant Analysis of Nonlinear Fractional Ordinary Differential Equations with Riemann-Liouville Fractional Derivative. Nonlinear Dynamics, 80, 447-455. https://doi.org/10.1007/s11071-014-1881-4
- 7. Odibat, Z. and Momani, S. (2009) The Variational Iteration Method: An Efficient Scheme for Handling Fractional Partial Differential Equations in Fluid Mechanics. Computers and Mathematics with Applications, 58, 2199-2208. https://doi.org/10.1016/j.camwa.2009.03.009
- 8. Wu, G. and Lee, E.W.M. (2010) Fractional Variational Iteration Method and Its Application. Physics Letters A, 374, 2506-2509. https://doi.org/10.1016/j.physleta.2010.04.034
- 9. Momani, S. and Odibat, Z. (2007) Comparison between the Homotopy Perturbation Method and the Variational Iteration Method for Linear Fractional Partial Differential Equations. Computers and Mathematics with Applications, 54, 910-919. https://doi.org/10.1016/j.camwa.2006.12.037
- 10. Sahadevan, R. and Bakkyaraj, T. (2015) Invariant Subspace Method and Exact Solutions of Certain Nonlinear Time Fractional Partial Differential Equations. Fractional Calculus and Applied Analysis, 18, 146-162. https://doi.org/10.1515/fca-2015-0010
- 11. Harris, P.A. and Garra, R. (2013) Analytic Solution of Nonlinear Frac-tional Burgers-Type Equation by Invariant Subspace Method. Nonlinear Studies, 20, 471-481.
- 12. Sahadevan, R. and Prakash, P. (2016) Exact Solution of Certain Time Fractional Nonlinear Partial Differential Equations. Nonlinear Dy-namics, 85, 659-673. https://doi.org/10.1007/s11071-016-2714-4
- 13. Zayed, E.M.E., Amer, Y.A. and Shohib, R.M.A. (2016) The Fractional Complex Transformation for Nonlinear Fractional Partial Differential Equations in the mathematical Physics. Journal of the Association of Arab Universities for Basic and Applied Sciences, 19, 59-69. https://doi.org/10.1016/j.jaubas.2014.06.008
- 14. Li, Z.B., Zhu, W.H. and He, J.H. (2012) Exact Solutions of Time-Fractional Heat Conduction Equation by the Fractional Complex Transform. Thermal Science, 16, 335-338. https://doi.org/10.2298/TSCI110503069L
- 15. Li, Z.B. and He, J.H. (2010) Fractional Complex Transform for Fractional Differential Equations. Mathematical and Computational Applications, 15, 970-973. https://doi.org/10.3390/mca15050970
- 16. Chen, J., Liu, F. and Anh, V. (2008) Analytical Solution for the Time-Fractional Telegraph Equation by the Method of Separating Variables. Journal of Mathematical Analysis and Ap-plications, 338, 1364-1377. https://doi.org/10.1016/j.jmaa.2007.06.023
- 17. Jiang, H., Liu, F., Turner, I., et al. (2012) Analytical Solutions for the Multi-Term Time-Fractional Diffusion-Wave/Diffusion Equations in a Finite Domain. Computers and Mathematics with Applications, 64, 3377-3388. https://doi.org/10.1016/j.camwa.2012.02.042
- 18. Luchko, Y. (2010) Some Uniqueness and Existence Results for the Initial-Boundary-Value Problems for the Generalized Time-Fractional Diffusion Equation. Computers and Mathe-matics with Applications, 59, 1766-1772. https://doi.org/10.1016/j.camwa.2009.08.015
- 19. Rui, W. (2020) Dynamical System Method for Investigating Ex-istence and Dynamical Property of Solution of Nonlinear Time-Fractional PDEs. Nonlinear Dynamics, 99, 2421-2440. https://doi.org/10.1007/s11071-019-05410-x
- 20. Rui, W. (2022) Separation Method of Semi-Fixed Variables To-gether with Dynamical System Method for Solving Nonlinear Time-Fractional PDEs with Higher-Order Terms. Nonlin-ear Dynamics, 109, 943-961.