Pure Mathematics
Vol.07 No.01(2017), Article ID:19492,4
pages
10.12677/PM.2017.71003
Global Asymptotic Stability of the Second-Order Nonlinear Difference Equation 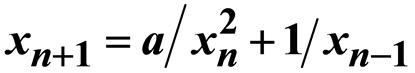
Xuguang Qin, Wei Feng
School of Mathematics and Systems Science, Beihang University, Beijing
Received: Dec. 22nd, 2016; accepted: Jan. 9th, 2017; published: Jan. 12th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper the global asymptotic stability of nonlinear difference equation 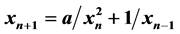 is investigated, where
is investigated, where 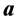 and the initial conditions
and the initial conditions 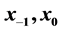 are positive real numbers. We show that both of the unique positive equilibrium and the unique period-2 solution are not globally asymptotically stable. In particular, our results solve one open problem proposed by V. L. Kocic and G. Ladas in monograph [1] , and partly solve another open problem proposed by them.
are positive real numbers. We show that both of the unique positive equilibrium and the unique period-2 solution are not globally asymptotically stable. In particular, our results solve one open problem proposed by V. L. Kocic and G. Ladas in monograph [1] , and partly solve another open problem proposed by them.
Keywords:Global Asymptotic Stability, Period-2 Solution, Equilibrium

二阶差分方程 的 全局渐近稳定性
的 全局渐近稳定性
秦旭光,冯伟
北京航空航天大学数学与系统科学学院,北京

收稿日期:2016年12月22日;录用日期:2017年1月9日;发布日期:2017年1月12日

摘 要
本文研究了非线性差分方程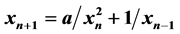 ,当参数
,当参数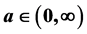 ,初值满足
,初值满足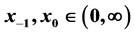 时的全局渐近稳定性。我们给出了方程的正平衡点和二周期解都不具有全局渐近稳定性的结论。特别的,解决了V. L. Kocic和G. Ladas著作 [1] 中的一个公开问题,部分解决了另一个公开问题。
时的全局渐近稳定性。我们给出了方程的正平衡点和二周期解都不具有全局渐近稳定性的结论。特别的,解决了V. L. Kocic和G. Ladas著作 [1] 中的一个公开问题,部分解决了另一个公开问题。
关键词 :全局渐近稳定,二周期解,平衡点

1. 引言
高阶非线性差分方程
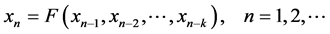
自V. L. Kocic和G. Ladas在文献 [1] 中对方程解的全局行为做了深入的研究后,差分方程解的全局行为成为人们研究的热门课题。差分方程平衡点的全局渐近稳定性、解的有界性、半环的性质及周期解的存在性也是文献 [1] 研究的主要内容。同时V. L. Kocic和G. Ladas在文献 [1] 中给出了一些有趣的公开问题,希望能激起读者的兴趣并进行深入的研究。该领域现在仍处于未成熟阶段,国内李先义和朱德明在差分方程领域做出了一些很好的成果,详见文献 [2] 。关于差分方程定性理论的背景及一些研究成果,参阅文献 [3] [4] [5] [6] 。
这篇文章我们就文献 [1] 的一个公开问题进行了探讨,主要研究了差分方程
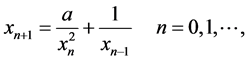 (1)
(1)
参数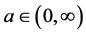 ,初值满足
,初值满足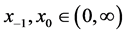 的动力学行为。
的动力学行为。
如果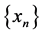 对于(1)所有
对于(1)所有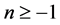 成立,我们就说
成立,我们就说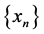 是方程(1)的一个解。如果
是方程(1)的一个解。如果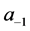 和
和 是两个给定的正实数,方程(1)有唯一的一个解
是两个给定的正实数,方程(1)有唯一的一个解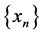 满足初值
满足初值 ,
,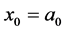 。显然对于
。显然对于 有
有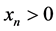 成立。下面我们只考虑方程(1)的正解。
成立。下面我们只考虑方程(1)的正解。
方程(1)有唯一的一个正平衡点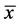 ,
,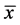 是三次方程
是三次方程 的唯一正根。
的唯一正根。
在文献 [1] 中,V. L. Kocic和G. Ladas研究了方程(1)的局部渐近稳定性,和二周期解的性质,我们概括如下。
定理A:方程(1)的正平衡点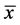 当
当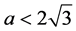 时是局部渐近稳定的,当
时是局部渐近稳定的,当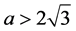 时是不稳定的。当
时是不稳定的。当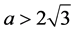 时,方程(1)有一个二周期解,
时,方程(1)有一个二周期解,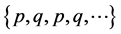 ,其中
,其中
 ,
,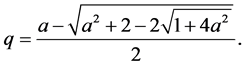
公开问题1:
(a) 当参数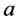 取何值时,(1)的平衡点
取何值时,(1)的平衡点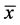 是全局渐近稳定的?
是全局渐近稳定的?
(b) 当参数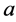 取何值时,(1)的二周期解
取何值时,(1)的二周期解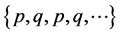 全局渐近稳定?
全局渐近稳定?
公开问题2:
考虑方程
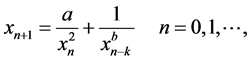 (2)
(2)
参数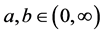 ,
, 且初值
且初值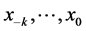 是任意的正实数。
是任意的正实数。
(a) 参数 满足什么条件时方程(2)的平衡点全局渐近稳定?
满足什么条件时方程(2)的平衡点全局渐近稳定?
2. 主要结论
定理1:当参数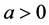 时,方程(1)的平衡点
时,方程(1)的平衡点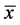 不是全局渐近稳定的。
不是全局渐近稳定的。
证明:关于方程(1)的平衡点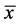 ,由
,由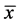 是三次方程
是三次方程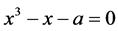 的唯一正根,容易验证
的唯一正根,容易验证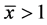 。对于正的初值
。对于正的初值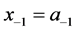 ,
,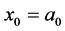 ,我们有
,我们有
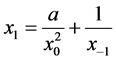 ,因此
,因此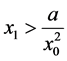 (3)
(3)
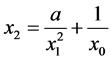 ,因此
,因此 (4)
(4)
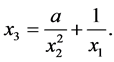 (5)
(5)
由上面三式,可以得到
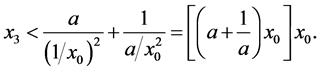 (6)
(6)
因此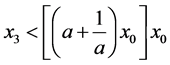 ,对于给定的参数
,对于给定的参数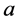 ,我们选取
,我们选取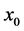 且使得
且使得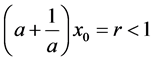 ,因此
,因此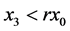 。如此重复上述步骤,可得
。如此重复上述步骤,可得 ,当
,当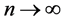 时,有
时,有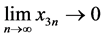 ,所以平衡点
,所以平衡点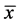 不是全局渐近稳定的。
不是全局渐近稳定的。
同理:
定理2:当参数 时,方程(1)的二周期解
时,方程(1)的二周期解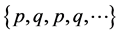 不是全局渐近稳定的。
不是全局渐近稳定的。
定理3:当参数 时,对于任意的参数
时,对于任意的参数 ,方程(2)的平衡点都不是全局渐近稳定的。
,方程(2)的平衡点都不是全局渐近稳定的。
注1:定理1对公开问题1的(a)做出了一个否定的回答,定理2对公开问题1的(b)给出了一个否定的回答,从而由定理1和定理2彻底解决了公开问题1。
注2:定理3部分解决了公开问题2的(a)。
文章引用
秦旭光,冯 伟. 二阶差分方程xn+1=a/xn2+1/xn-1 的全局渐近稳定性
Global Asymptotic Stability of the Second-Order Nonlinear Difference Equation xn+1=a/xn2+1/xn-1[J]. 理论数学, 2017, 07(01): 16-19. http://dx.doi.org/10.12677/PM.2017.71003
参考文献 (References)
- 1. Kocic, V.L. and Ladas, G. (1993) Global Behavior of Nonlinear Difference Equations of Higher Order with Applications. Springer, 162-165. https://doi.org/10.1007/978-94-017-1703-8
- 2. 李先义. 几类微分差分方程的稳定性理论研究[D]: [博士学位论文]. 上海: 华东师范大学, 2003.
- 3. Lyapunov, A.M. (1992) The General Problem of the Stability of Motion. International Journal of Control, 55, 531- 773. https://doi.org/10.1080/00207179208934253
- 4. Kalman, R.E. and Bertram, J.E. (1959) Control System Analysis and Design via the Second Method of Lyapunov: (i) Continuous-Time Systems, (ii) Discrete-Time Systems. IRE Transactions on Automatic Control, 4, 112. https://doi.org/10.1109/TAC.1959.1104895
- 5. 王慕秋, 王联. 离散动力系统的稳定性[J]. 数学季刊, 1987, 2(3): 12-30.
- 6. Kelley, W.G. and Peterson, A.C. (2001) Difference Equations an Introduction with Applications. Harcourt/Academic Press.