Applied Physics
Vol.
10
No.
11
(
2020
), Article ID:
38793
,
9
pages
10.12677/APP.2020.1011061
基于晶格动力学的硅单晶热学性质研究(II)——晶格非和谐势能和格律纳森参数
贺业鹏,黄建平*
湖南师范大学信息科学与工程学院,湖南 长沙
收稿日期:2020年11月5日;录用日期:2020年11月19日;发布日期:2020年11月26日

摘要
为用晶格动力学方法研究硅单晶的热膨胀性质,必须首先计算作为微扰哈密顿的硅单晶晶格的三阶非和谐势能,而三阶非和谐势能的计算又可以建立在已知不同晶格常数所对应的晶格和谐势能的基础上,因此本文运用他人计算得到的最近邻和次近邻原子间的相互作用力常数,推导了的硅单晶的晶格和谐势能公式,并在此基础上根据不同晶格常数下的晶格和谐势能推导了三阶非和谐势能公式,为后续硅单晶的热膨胀系数计算公式的推导做了必要准备。最后还运用本文提出的三阶非和谐势能模型,计算了不同温度下硅单晶的格律纳森参数,发现其与他人的实验结果吻合,从而验证了本文所提出的三阶非和谐势能模型的正确性。
关键词
硅单晶,热膨胀,晶格动力学,力常数,非和谐势能,格律纳森参数
Study on Thermal Properties of Silicon Single Crystal Based on Lattice Dynamics (II)—Lattice Anharmonic Potential and Gruneisen Parameter
Yepeng He, Jianping Huang*
College of Information Science and Technology, Hunan Normal University, Changsha Hunan

Received: Nov. 5th, 2020; accepted: Nov. 19th, 2020; published: Nov. 26th, 2020

ABSTRACT
Abstract: In order to study the thermal expansion properties of silicon single crystal by lattice dynamics, the third order anharmonic potential of silicon single crystal lattice should be calculated as the perturbation Hamiltonian first, and the calculation of the third order anharmonic potential can be based on the lattice harmonic potential corresponding to different lattice constants. Therefore, the formula for lattice harmonic potential energy of silicon single crystal is derived first by using the interaction force constants between the nearest neighbor atoms and the next-nearest neighbor atoms calculated by others, and then the formula for the third order anharmonic potential is derived based on the lattice harmonic potential with different lattice constants. It is a necessary preparation for the subsequent derivations of formula for thermal expansion coefficient. Finally, with the third-order anharmonic potential energy model proposed in this paper, the Gruneisen parameters of silicon single crystal at different temperature are calculated, and it coincides with the experimental results of others. Thus the correctness of the third-order anharmonic potential energy model proposed in this paper is verified.
Keywords:Silicon Single Crystal, Thermal Expansion, Lattice Dynamics, Force Constant, Anharmonic Potential, Gruneisen Parameter

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在文献 [1] 中,我们给出了硅单晶的晶格动力学矩阵,对该矩阵求解本征值问题,即可求得和谐晶体的晶格振动频率和晶格振动位移。用晶格动力学研究硅单晶的热膨胀性质的思路是,将和谐晶体的晶格振动状态作为未微扰态,将硅单晶晶格的三阶非和谐势能作为微扰哈密顿,利用量子力学的微扰论推导原子间距的热膨胀和热膨胀系数公式,在此基础上进行数值计算并进而分析热膨胀机制 [2] [3] [4]。根据在不同晶格常数下的和谐势能,可以得到三阶非和谐势能,即微扰哈密顿。本文将推导硅单晶的和谐势能公式和三阶非和谐势能公式,为热膨胀公式的推导做准备。
格律纳森定律给出了热膨胀系数 与单位体积的比热 之间的关系 [5]
(1)
其中, 为格律纳森参数,B为体积模量。如果知道格律纳森参数 ,体积模量B,即可计算得到热膨胀系数 ,所以格律纳森参数对材料的热膨胀性质研究是十分重要的 [6]。因此,最后还将运用本文提出的三阶非和谐势能模型,计算不同温度下硅单晶的格律纳森参数,并将其与他人的实验结果相比较,从而验证本文所提出的三阶非和谐势能模型的正确性,还将基于格律纳森参数 公式对不同的三阶力常数对硅单晶热膨胀性质的影响进行了分析与研究。
2. 原子间两体和谐势能
最近邻原子间存在两体相互作用力,该作用力是中心力,大小与两原子间的距离变化量成正比,其弹性系数设为k,则原子O与最近邻原子A、B、C和D之间的两体作用和谐势能可表示为:
(2)
其中, 、 、 和 分别为原子A和O、原子B和O、原子C和O及、原子D和O间的距离变化量。
(3)
(4)
(5)
(6)
在(3)式~(6)式中, 表是原子 相对于原子 在 方向的位移,即 。
3. 原子间三体和谐势能
以原子A、O和B为例,它们组成了一个等腰三角形,原子O处于其顶角,原子A和O、原子B和O互为近邻原子,原子A和原子B互为次近邻原子,现只考虑这三个原子间的三体相互作用,并将原子A、O和B之间三体相互作用势按泰勒级数展开,其二阶和谐势能可表示为,
(7)
其中, 和 分别代表原子 和 的晶格振动在 和 方向上的位移, 为原子 和 之间的力常数, 和 可以为A、O或B。由于O处于等腰三角形AOB的顶角,根据对称性及原子A、O或B的位置关系,可设
(8)
设原子A、O和B之间没有相对运动,则原子A所受合力为0,则有 [1]
(9)
根据(8)式、(9)式和原子A、B之间的力常数矩阵 [1]
(10)
可得
(11)
由于 是对称矩阵,因此上式中 ,所以有
(12)
(13)
根据对称性,由(12)和(13)式可得以下两式
(14)
(15)
同理根据 [1]
(16)
可得
(17)
将以上的力常数矩阵代入(7)式,得原子A、B和C之间的三体和谐势能
(18)
由于文献中 [7] 的数据可知, 非常接近于0,且可以从对称性加以证明
(19)
(20)
其中,共有三项,分别与A原子和O原子、B原子和O原子,以及A原子和B原子之间的相对运动有关。根据硅晶体的结构,与原子O最近邻的原子还有原子B、C、D,根据对称性,由(18)式并根据对称性,得以原子O为顶点的等腰三角形AOC、AOD的势能
(21)
(22)
根据硅晶体的结构,与原子A最近邻的原子除O外还有 、 、 ,根据以上方法,同样可得以原子A为顶点的等腰三角形 、 和 的势能
(23)
(24)
(25)
以上(20)式~(25)式是共有OA键的所有三体和谐势公式。
同样可以分别计算共有BO键、共有CO键和共有DO键的六个三体势,显然,计算重复了一倍,因此在整个晶体内对它们求和之后应该将求和结果除以2。
根据对称性,把三体和谐势能的所有结果相加,得:
(26)
其中, 和 为与原子O与最近邻的所有1类原子A、B、C和D, 和 为与原子A与最近邻的所有2类原子O、 、 和 。 为三体势中与原子 和O间相对运动有关的相互作用势能,可表示为:
(27)
其中, 可根据(3)~(6)式计算,为原子O与所有最近邻原子A、B、C和D间的键长变化量。 为原子O与所有最近邻原子A、B、C和D间位移之差的模的平方。
(28)
(26)式中, 为三体势中与原子 和 之间相对运动有关的势能, 为三体势中与原子 、 之间相对运动有关的势能,不重复计算。
、 、 和 可表示为
(29)
、 、 和 可表示为
(30)
、 、 和 可表示为
(31)
以上各式中, 。
根据(2)式和(27)式,可以得到与原子O、 间相对运动有关的总相互作用势能
(32)
根据力常数定义式 [1],可知 ,,最后可将(32)式表示为
(33)
由(29)~(31)式以及(33)式可知,和谐晶体晶格振动势能与力常数存在线性关系,因此相关各项中写入相关力常数 。综合各式可得
(34)
根据Rignanese等人 [7] 从第一性原理出发,计算得到的二阶力常数 、 、 和 ,及在参考文献 [1] 中我们给出的晶格振动位移,利用(34)式即可计算晶格和谐势能。
4. 原子间三阶非和谐势能
在研究晶格热学性质时,一般采用泰勒级数对原子间相互作用势能进行展开,在一般无需考虑非和谐势能的情况下,只需展开至二次项,在计算热传导和热膨胀时,才需要展开至三次以上的高次项。由于四次非和谐势能相对于平衡位置是对称的,因而不会对热膨胀有贡献,因此作为很好的近似,在计算热膨胀时只需展开至三次非和谐势能项。以下根据和谐势能项公式,和力常数对晶格常数的导数,计算三阶非和谐势能。
根据Rignanese等人在参考文献 [7] 中给出的晶格常数下的二阶力常数 、 、 和 ,可以计算力常数 、 、 和 对晶格常数的一阶导数 、 、 和 。由上式可得晶格振动势能对晶格常数的导数
(35)
可见,只需将和谐势能公式中的力常数用其对晶格常数的导数替代即可得晶格振动势能对晶格常数的导数。
由各方向晶格常数的变化 引起的晶格体积的变化为
(36)
再根据 可得
(37)
上式中,
(38)
(39)
(40)
将(38)式~(40)式代入(37)式,得
(41)
上式中, 为原子间距离的变化量。根据我们在参考文献 [1] 中给出的晶格振动位移公式、和根据Rignanese给出的不同晶格常数下力常数而得到的力常数对晶格常数的导数,即可根据上式计算三阶非和谐势能。
5. 格律纳森参数
在准和谐近似(QHA)下,格律纳森参数 可以通过下式计算 [5]
(42)
其中, 为 模态声子的每单位体积的比热,而 为其总和, 为模态格律纳森参数, 和 分别由下式定义
(43)
(44)
由上式和(42)式可知,格律纳森参数ρ无量纲。将(43)式和(44)式代入(42)式,并将体积用晶格常数表示,得:
(45)
上式中对求和号内各项求和即得所有声子能量总和,即为晶格振动能量E,其包含动能 和 势能。与此相对应,系统哈密顿算子H也有动能哈密顿算子 和势能哈密顿算子 (即势能U)这两部分构成,能量为对应哈密顿算子的热力学平均值,即 ,,。因此,上式变为
(46)
由于热膨胀会引起晶格常数的变化,只会导致其势能哈密顿的变化,因而由上式得,
(47)
将(34)式代入上式,并考虑到由于 和 比 和 小很多,可以忽略(34)式中第二和第三项,并考虑到由于晶体结构对称性第一项求和式中所有四项所产生的热膨胀都等于 ,得
(48)
将(2)式、(28)式和(33)代入上式,得
(49)
将文献(1)中的公式(26)代入,得
(50)
根据Rignanese等人在参考文献 [7] 中提供的不同晶格常数下的二阶力常数 和 而计算出的它们对晶格常数的一阶导数 和 ,并代入上式可计算不同温度下的格律纳森参数 ,结果如图1所示,图中还列出了为了Ibach的实验结果 [8],可见我们的计算结果与实验数据能较好地吻合,说明本文给出的原子间三阶非和谐势能模型及格律纳森参数 公式是正确的。
由于(1)式中的体积模量B和单位体积的比热 都为正值,因此,热膨胀系数的正负取决于格律纳森参数 的正负,图1中硅单晶在约120 K温度下格律纳森参数为负,表明在该温度段有负热膨胀系数,而在其它温度段的格律纳森参数 为正,表明有正的热膨胀系数。根据 和 得知 为正、 为负,由(50)式可知,这就有可能使得某些模态的声子对格律纳森参数 形成正的贡献,而又有些模态的声子对格律纳森参数 形成负的贡献,并且随温度的变化,各个模态对格律纳森参数 贡献的大小也会有相应的调整,从而使得格律纳森参数 在不同温度段呈现不同的正负特性,例如硅单晶在约120 K温度下呈现反常的负热膨胀的性质,而在高温下呈现正常的正热膨胀性质。在后续的论文中,我们将在晶格动力学和微扰论的基础上对硅单晶的热膨胀系数公式进行严密的推导,并在数值计算的基础上更为详细探讨硅单晶低温负热膨胀性质的物理机制。
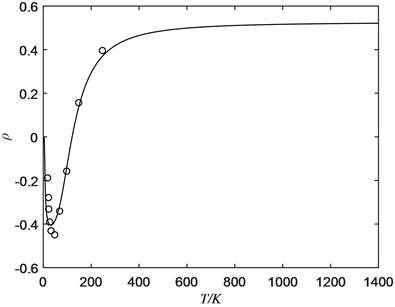
Figure 1. The gruneisen constant of silicon single crystal vs temperature
图1. 硅单晶的格律纳森常数与温度的关系
6. 结论
本文运用他人计算得到的最近邻和次近邻原子间的相互作用力常数,推导了的硅单晶的晶格和谐势能公式,并在此基础上根据不同晶格常数下的晶格和谐势能推导了三阶非和谐势能公式。本文还根据这个三阶非和谐势能模型,推导了在准和谐近似(QHA)下计算硅单晶的格律纳森参数公式,并将计算结果与他人的实验结果进行了比较,从而证明了本文提出的三阶非和谐势能模型是正确的,这为后续硅单晶的热膨胀系数的计算做了必要准备。本文最后对硅单晶的负热膨胀的物理机制进行了初步分析,认为因为 为正、 为负,这使得某些模态的声子对格律纳森参数 形成正的贡献,而又有些模态的声子对格律纳森参数 形成负的贡献,并且随温度的变化,各个模态对格律纳森参数 贡献的大小也会有相应的调整,从而使得格律纳森参数 在不同温度段呈现不同的正负特性,从而使硅单晶在约120 K温度下呈现反常的负热膨胀的性质,而在高温下呈现正常的正热膨胀性质。
文章引用
贺业鹏,黄建平. 基于晶格动力学的硅单晶热学性质研究(II)——晶格非和谐势能和格律纳森参数
Study on Thermal Properties of Silicon Single Crystal Based on Lattice Dynamics (II)—Lattice Anharmonic Potential and Gruneisen Parameter[J]. 应用物理, 2020, 10(11): 467-475. https://doi.org/10.12677/APP.2020.1011061
参考文献
- 1. 贺业鹏, 黄建平. 基于晶格动力学的硅单晶热学性质研究(I)——晶格动力学与比热[J]. 应用物理, 2020, 10(11): 459-466. https://doi.org/10.12677/app.2020.1011060
- 2. Huang, J., Wu, X. and Li, S. (2005) Thermal Expansion Coefficients of Thin Crystal Films. Communications in Theoretical Physics, 44, 921-924. https://doi.org/10.1088/6102/44/5/921
- 3. 黄建平, 胡诗一. 基于原子间相互作用的低温硅单晶负热膨胀机制的研究[J]. 原子与分子物理学报, 2014, 31(5): 851-854.
- 4. 蔡建华. 量子力学[M]. 北京: 人民教育出版社, 1980: 67-72.
- 5. Wei, S., Li, C. and Chou, M.Y. (1994) Ab Initio Calculation of Thermodynamic Properties of Silicon. Physical Review B, 50, 14587-14590. https://doi.org/10.1103/PhysRevB.50.14587
- 6. Cuffari, D. and Bongiorno, A. (2020)Calculation of Mode Grüneisen Parameters Made Simple. Physical Review Letters, 124, Article: ID: 215501. https://doi.org/10.1103/PhysRevLett.124.215501
- 7. Rignanese, G.M., Michenaud, J.P. and Gonze, X. (1996) Ab Initio Study of the Volume Dependence of Dynamical and Thermodynamical Properties of Silicon. Physical Review B, 53, 4488-4497. https://doi.org/10.1103/PhysRevB.53.4488
- 8. Ibach, H. (1969) Thermal Expansion of Silicon and Zinc Oxide (I). Physica Status Solidi, 31, 625-634. https://doi.org/10.1002/pssb.19690310224
NOTES
*通讯作者。