(3 + 1)维修正KdV-ZK方程和(3 + 1)维KP方程的精确行波解 Exact Traveling Wave Solutions of the (3 + 1)-Dimensional Modified KdV-ZK Equation and the (3 + 1)-Dimensional KP Equation

doi:10.12677/AAM.2022.113096

Advances in Applied Mathematics
Vol. 11 No. 03 ( 2022 ), Article ID: 49154 , 8 pages
10.12677/AAM.2022.113096

(3 + 1)维修正KdV-ZK方程和(3 + 1)维KP方程的精确行波解

曾职云^*，张练，叶飞筠

●How to Cite this Article

贵州民族大学，数据科学与信息工程学院，贵州贵阳

收稿日期：2022年2月3日；录用日期：2022年2月28日；发布日期：2022年3月7日

摘要

本文讨论了(3 + 1)维修正KdV-Zakharov-Kuznetsov方程和(3 + 1)维Kadomtsev-Petviashvili方程的精确行波解，得到了(3 + 1)维修正KdV-Zakharov-Kuznetsov方程的扭状孤波解和(3 + 1)维Kadomtsev-Petviashvili方程的双曲函数奇异解，并且利用Maple软件给出了解的3D和2D图，分析了解在特殊参数值下的动力行为。

关键词

行波解，(3 + 1)维修正KdV-Zakharov-Kuznetsov方程，(3 + 1)维Kadomtsev-Petviashvili方程

Exact Traveling Wave Solutions of the (3 + 1)-Dimensional Modified KdV-ZK Equation and the (3 + 1)-Dimensional KP Equation

Zhiyun Zeng^*, Lian Zhang, Feiyun Ye

College of Data Science and Information Engineering, Guizhou Minzu University, Guiyang Guizhou

Received: Feb. 3^rd, 2022; accepted: Feb. 28^th, 2022; published: Mar. 7^th, 2022

ABSTRACT

In this paper, we discuss the exact traveling wave solutions of the (3 + 1)-dimensional modified KdV-Zakharov-Kuznetsov equation and the (3 + 1)-dimensional Kadomtsev-Petviashvili equation, the twisted solitary wave solutions of the (3 + 1)-dimensional modified KdV-Zakharov-Kuznetsov equation and the hyperbolic function singular solutions of the (3 + 1)-dimensional Kadomtsev-Petviashvili equation were obtained; the 3D and 2D plots of the solutions were given with Maple, analyzing the dynamic behavior of the solutions under the particular parameters value.

Keywords:Traveling Wave Solution, The (3 + 1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation, The (3 + 1)-Dimensional Kadomtsev-Petviashvili Equation

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

非线性发展方程在许多领域中有着广泛的应用，例如在流体力学、固体物理、生物和海洋工程、光纤、等离子体物理和化学物理等领域中，涌现出类似于薛定谔方程 [1] 、KdV方程 [2] 等许多重要的非线性发展方程。如今，人们提出了许多有效的方法去构造非线性发展方程的精确行波解，如 $(G^{'} / G, 1 / G)$ 扩展法 [3] [4] ，正弦–余弦方法 [5] ， $e^{(- Φ (ξ))}$ 函数法 [6] [7] ，Jacobi椭圆函数法 [8] [9] ，tanh函数法 [10] ，扩展的直接代数法及新的扩展的直接代数法 [11] [12] [13] ， $(G^{'} / G)$ 扩展法 [14] [15] ，F-扩展法 [16] [17] ，映射法和扩展映射法 [18] ， $(1 / G^{'})$ 扩展法 [19] [20] [21] [22] 等。

本文主要用 $(1 / G^{'})$ 扩展法构造(3 + 1)维修正KdV-Zakharov-Kuznetsov方程 [14] (简称mKdV-ZK方程)

$u_{t} + α u^{2} u_{x} + u_{x x x} + u_{x y y} + u_{x z z} = 0$ (1)

和(3 + 1)维Kadomtsev-Petviashvili方程 [3] (简称KP方程)的精确行波解。

${(u_{t} + 6 u u_{x} + u_{x x x})}_{x} - 3 u_{y y} - 3 u_{z z} = 0$ (2)

方程(1)中包含四项耗散效应 $u_{t}, u_{x x x}, u_{x y y}, u_{x z z}$ 和一个对流过程 $u^{2} u_{x}$ 。在均匀磁场存在的情况下，方程(1)控制弱非线性离子声波的行为，包括冷离子和热等温电子的等离子体。1970年，Kadomtsev和Petviashvili在研究散色和非线性介质中的非线性波动理论时提出了KP方程，该方程是描述浅水波和等离子声波的方程，且在很多领域都有重要的应用。Zhang Z Y [8] 利用Jacobi椭圆函数展开法得到了方程(1)精确的行波解；Uttam Ghosh [23] 利用修正分数阶子方程方法得到了方程(1)的精确解析解；Md. Nur Alam [24] 利用一种 $(G^{'} / G)$ 扩展法获得了方程(1)一些新的和更一般的行波解。Ma W X [25] 总结了方程(2)的行波解和有理解；Zayed E M E [26] 利用 $(G^{'} / G, 1 / G)$ 扩展法得到方程(2)的孤立波解和三角周期解；Lu D [27] 运用拟设法获得了方程(2)的孤立波解、冲击波解和奇异波解等。

本文结构为：在第二部分，给出 $(1 / G^{'})$ 扩展法的具体步骤；在第三部分，利用 $(1 / G^{'})$ 扩展法构造了(3 + 1)维修正KdV-Zakharov-Kuznetsov方程和(3 + 1)维Kadomtsev-Petviashvili方程的精确行波解；在第四部分，对行波解的图形性态进行分析；总结在第五部分。

2. $(1 / G^{'})$ 扩展法的步骤

考虑如下非线性偏微分方程

$F (u, \frac{\partial u}{\partial t}, \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial^{2} u}{\partial x^{2}}, \dots) = 0$ (3)

令行波变换

$u = u (ξ) = u (x, y, z, t), ξ = x + y + z - c t, c \neq 0$ (4)

其中c是波速。在方程(3)中用行波变换(4)可得如下常微分方程

$P (U, U', U ″, \dots) = 0$ (5)

$' = \frac{\partial U}{\partial ξ}$ 。假定方程(5)有如下形式的解

$U (ξ) = a_{0} + \sum_{i = 1}^{n} a_{i} {(\frac{1}{G^{'} (ξ)})}^{i}$ (6)

其中 $a_{i} (i = 0, 1, \dots, n)$ 为待定常数，n由齐次平衡原则确定， $G = G (ξ)$ 满足二阶常微分方程

$G ″ + κ G' + μ = 0$ (7)

其中 $κ, μ$ 是参数，方程(7)有如下形式的解 [19]

$\frac{1}{G^{'} (ξ)} = \frac{1}{- \frac{μ}{κ} + A \cosh (ξ κ) - A \sinh (ξ κ)}$ (8)

将 $U (ξ)$ 以及 $U (ξ)$ 的各阶导数与方程(7)代入方程(5)中，合并 ${(\frac{1}{G^{'}})}^{i}$ $(i = 0, 1, \dots, n)$ 的次数，得到一个关于 $a_{0}, a_{1}, \dots, a_{n}$ 的代数方程组，再借助解(8)可得出方程(3)的精确行波解。

3. 精确行波解

在本部分利用 $(1 / G^{'})$ 扩展法构造(3 + 1)维修正KdV-Zakharov-Kuznetsov方程和(3 + 1)维Kadomtsev-Petviashvili方程的精确行波解。

3.1. mKdV-ZK方程的精确行波解

将行波变换(4)代入方程(1)可得

$- c u' + α u^{2} u' + 3 u^{‴} = 0$ (9)

其中c是波速。对方程(9)积分一次，并令积分常数为零，则

$- c u + \frac{1}{3} α u^{3} + 3 u ″ = 0$ (10)

根据最高阶导数项 $u^{″}$ 与非线性项 $α u^{3}$ 的平衡原则，可得 $n = 1$ 。再由方程(6)可设方程(10)有如下形式的解

$u (ξ) = a_{0} + a_{1} (\frac{1}{G'})$ (11)

其中 $a_{0}, a_{1}$ 是待定常数，将方程(11)以及 $u (ξ)$ 的相关导数与方程(7)代入方程(10)，合并同类项令 ${(\frac{1}{G^{'}})}^{i}$ $(i = 0, 1, 2, 3)$ 的系数为0，得到关于 $a_{0}, a_{1}$ 与c的代数方程组为：

$\begin{array}{l} {(\frac{1}{G^{'}})}^{0} : - a_{0} c + \frac{1}{3} α a_{0}^{3} = 0 \\ {(\frac{1}{G^{'}})}^{1} : - a_{1} c + α a_{0}^{2} a_{1} + 3 a_{1} κ^{2} = 0 \\ {(\frac{1}{G^{'}})}^{2} : α a_{0} a_{1}^{2} + 9 a_{1} κ μ = 0 \\ {(\frac{1}{G^{'}})}^{3} : \frac{1}{3} α a_{1}^{3} + 6 a_{1} μ^{2} = 0 \end{array}$ (12)

求解上述方程组可得：

$a_{0} = \pm \sqrt{\frac{3 c}{α}}, a_{1} = - \frac{9 κ μ}{α a_{0}}, c = - \frac{3 κ^{2}}{2}$ (13)

将方程(13)和方程(8)代入方程(11)，得出方程(1)有如下形式的双曲函数解：

$u_{1} (ξ) = \pm \frac{3 \sqrt{2 α}}{α} i [\frac{κ}{2} + \frac{μ}{- \frac{μ}{κ} + A \cosh (ξ κ) - A \sinh (ξ κ)}]$ (14)

由 $(1 / G^{'})$ 扩展法得到的双曲函数解(14)的3D、2D图如图1所示，其中 $ξ = x + y + z + \frac{3 κ^{2}}{2} t$ ， $κ, μ$ 为参数，i为虚数单位。

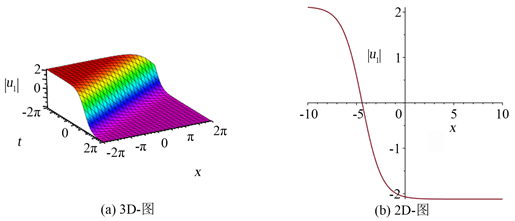
Figure 1. The 3D and 2D plots of solution (14)

图1. 解(14)的3D与2D图

3.2. KP方程的精确行波解

将行波变换(4)代入方程(2)可得

${(- c u' + 6 u u' + u^{‴})}^{'} - 6 u ″ = 0$ (15)

其中c表示波速。对方程(15)积分两次，令积分常数为零，可得

$- c u - 6 u + 3 u^{2} + u ″ = 0$ (16)

考虑 $ξ \to \pm \infty$ 时， $| u | \to 0$ ，根据最高阶导数项 $u ″$ 与非线性项 $u^{2}$ 的平衡原则，可得 $n = 2$ ，再由方程(6)可设方程(16)有如下形式的解

$u (ξ) = a_{0} + a_{1} (\frac{1}{G^{'}}) + a_{2} {(\frac{1}{G^{'}})}^{2}$ (17)

其中 $a_{0}, a_{1}, a_{2}$ 是待定常数，将方程(17)以及 $u (ξ)$ 的相关导数与方程(7)代入方程(16)，合并同类项令 ${(\frac{1}{G^{'}})}^{i}$ $(i = 0, 1, 2, 3, 4)$ 的系数为0，得到关于 $a_{0}, a_{1}, a_{2}$ 与c的代数方程组为：

$\begin{array}{l} {(\frac{1}{G^{'}})}^{0} : - a_{0} c - 6 a_{0} + 3 a_{0}^{2} = 0 \\ {(\frac{1}{G^{'}})}^{1} : - a_{1} c - 6 a_{1} + 6 a_{0} a_{1} + a_{1} κ^{2} = 0 \\ {(\frac{1}{G^{'}})}^{2} : - a_{2} c - 6 a_{2} + 3 a_{1}^{2} + 6 a_{0} a_{2} + 3 a_{1} κ μ + 4 a_{2} κ^{2} = 0 \\ {(\frac{1}{G^{'}})}^{3} : 3 a_{1} a_{2} + a_{1} μ^{2} + 5 a_{2} κ μ = 0 \\ {(\frac{1}{G^{'}})}^{4} : a_{2}^{2} + 2 a_{2} μ^{2} = 0 \end{array}$ (18)

求解上述方程组，得出如下解的情况：

情况1. $a_{0} = 0, a_{1} = - 2 κ μ, a_{2} = - 2 μ^{2}, c = κ^{2} - 6$ (19)

将方程(19)和方程(8)代入方程(17)，得出方程(2)有如下形式的双曲函数解：

$u_{2} (ξ) = - \frac{2 κ μ}{- \frac{μ}{κ} + A \cosh (ξ κ) - A \sinh (ξ κ)} - \frac{2 μ^{2}}{{(- \frac{μ}{κ} + A \cosh (ξ κ) - A \sinh (ξ κ))}^{2}}$ (20)

其中 $ξ = x + y + z - (κ^{2} - 6) t$ 。

情况2. $a_{0} = \frac{1}{3} (c + 6), a_{1} = - 2 κ μ, a_{2} = - 2 μ^{2}, c = - (κ^{2} + 6)$ (21)

将方程(21)和方程(8)代入方程(17)，得出方程(2)有如下形式的双曲函数解：

$u_{3} (ξ) = \frac{1}{3} (c + 6) - \frac{2 κ μ}{- \frac{μ}{κ} + A \cosh (ξ κ) - A \sinh (ξ κ)} - \frac{2 μ^{2}}{{(- \frac{μ}{κ} + A \cosh (ξ κ) - A \sinh (ξ κ))}^{2}}$ (22)

其中 $ξ = x + y + z + (κ^{2} + 6) t$ 。

Figure 2. The 3D and 2D plots of solution (20)

图2. 解(20)的3D与2D图

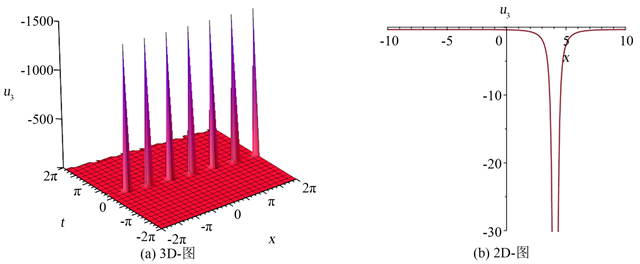
Figure 3. The 3D and 2D plots of solution (22)

图3. 解(22)的3D与2D图

4. 图像分析

图1是方程(1)的解 $u_{1}$ 在 $- 10 \leq x, t \leq 10$ 区间内，当参数 $μ = - 1, α = κ = y = z = 1, A = 0.4$ 时的3D性态，以及 $t = 1$ 时的2D性态。根据波向右传播，有一个波峰，且波的形状和速度保持不变，可知解 $u_{1}$ 为方程(1)的扭状孤波解。图2是方程(2)的解 $u_{2}$ 在 $- 10 \leq x, t \leq 10$ 区间内，当参数 $μ = κ = y = z = 1, A = 0.4, c = - 5$ 时的3D和 $t = - 1$ 时的2D性态。可以看出解 $u_{2}$ 有一个波谷，并且出现尖点，因此 $u_{2}$ 为方程(2)的非光滑奇异解。图3是方程(2)的解 $u_{3}$ 在 $- 10 \leq x, t \leq 10$ 区间内，当参数 $μ = κ = y = z = 1, A = 0.4, c = - 7$ 时的3D和 $t = - 1$ 时的2D性态。可以观察到解 $u_{3}$ 有一个波谷和尖点，因此 $u_{3}$ 为方程(2)的非光滑奇异解。

5. 总结

本文主要用 $(1 / G^{'})$ 扩展法构造了方程(1)和方程(2)的精确行波解，得到方程(1)的解为扭状孤波解，方程(2)的解为非光滑奇异解。做出了这些解在特殊参数值下的3D和2D图，并对这些解的性态进行了分析。

通过将解(14)与文献 [19] 中解(23)比较发现，若解(14)中令 $α = - 18$ 时，可得出解的形式为 $u_{1} (ξ) = - \frac{κ}{2} - \frac{μ}{- \frac{μ}{κ} + A \cosh (ξ κ) - A \sinh (ξ κ)}$ ，而解(23)中令 $a_{1} = - μ$ ，可得出相同形式的解。由此可见，

解(14)比解(23)更具有一般性。

致谢

我对本文进行审阅的各位老师表示由衷的感谢。

基金项目

贵州省科学技术厅基金[2019] (1162)。

文章引用

曾职云,张练,叶飞筠,安海钰,王建华. 基于结构方程模型的影响消费者接受社区电商购物模式的因素探究
Research on the Factors of Consumers’ Acceptance of Community E-Commerce Based on SEM[J]. 应用数学进展, 2022, 11(03): 906-913. https://doi.org/10.12677/AAM.2022.113097

参考文献

1. Zayed, E.M.E. and Al-Nowehy, A.-G. (2017) New Extended Auxiliary Equation Method for Finding Many New Jacobi Elliptic Functions Solutions of Three Nonlinear Schrödinger Equations. Waves in Random and Complex Media, 27, 420-439. https://doi.org/10.1080/17455030.2016.1259690

2. Wang, M., Li, X. and Zhang, J. (2008) The (G’/G)-Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423. https://doi.org/10.1016/j.physleta.2007.07.051

3. Mamun Miah, M., Seadawy, A.R. and Shahadat Alietal, H.M. (2019) Further Investigations to Extract Abundant New Exact Traveling Wave Solutions of Some NLEEs. Journal of Ocean Engineering and Science, 4, 387-394. https://doi.org/10.1016/j.joes.2019.06.004

4. Li, L., Li, E. and Wang, M. (2010) The (G’/G, 1/G)-Expansion Method and Its Application to Travelling Wave Solutions of the Zakharov Equations. Applied Mathematics—A Journal of Chinese Universities, 25, 454-462. https://doi.org/10.1007/s11766-010-2128-x

5. Ali, K.K., Seadawy, A.R., Yokus, A., Yilmazer, R. and Bulut, H. (2020) Propagation of Dispersive Wave Solutions for (3+1)-Dimensional Nonlinear Modified Zakharov-Kuznetsov Equation in Plasma Physics. International Journal of Modern Physics B, 34, Article ID: 2050227. https://doi.org/10.1142/S0217979220502276

6. Arshed, S. (2020) New Soliton Solutions to the Perturbed Nonlinear Schrödinger Equation by Exp(-Φ(ξ))-Expansion Method. Optik, 220, Article ID: 165123. https://doi.org/10.1016/j.ijleo.2020.165123

7. Elboree, M.K. (2021) Soliton Molecules and Exp(-Φ(ξ))-Expansion Method for the New (3+1)-Dimensional Kadomtsev-Petviashvili (KP) Equation. Chinese Journal of Physics, 71, 623-633. https://doi.org/10.1016/j.cjph.2021.04.001

8. Zhang, Z.Y. (2015) Jacobi Elliptic Function Expansion Method for the Modified Korteweg-de Vries-Zakharov-Kuznetsov and the Hirota Equations. Romanian Journal of Physics, 60, 1384-1394.

9. Zhou, Q., Ekici, M., Mirzazadeh, M., et al. (2017) The Investigation of Soliton Solutions of the Coupled Sine-Gordon Equation in Nonlinear Optics. Journal of Modern Optics, 64, 1677-1682. https://doi.org/10.1080/09500340.2017.1310318

10. Abdel-All, N.H., Abdel-Razek, M.A.A. and Seddeek, A.A.K. (2011) Expanding the Tanh-Function Method for Solving Nonlinear Equations. Applied Mathematics, 2, 1096-1104. https://doi.org/10.4236/am.2011.29151

11. Vahidi, J., Zabihi, A., Rezazadeh, H., et al. (2021) New Extended Direct Algebraic Method for the Resonant Nonlinear Schrödinger Equation with Kerr Law Nonlinearity. Optik, 227, Article ID: 165936. https://doi.org/10.1016/j.ijleo.2020.165936

12. Rezazadeh, H., Sabi’u, J., Jena, R.M., et al. (2020) New Optical Soliton Solutions for Triki-Biswas Model by New Extended Direct Algebraic Method. Modern Physics Letters B, 34, Article ID: 2150023. https://doi.org/10.1142/S0217984921500238

13. Rehman, H.U., Ullah, N. and Imran, M.A. (2021) Optical Solitons of Biswas-Arshad Equation in Birefringent Fibers Using Extended Direct Algebraic Method. Optik, 226, Article ID: 165378. https://doi.org/10.1016/j.ijleo.2020.165378

14. Alam, M.N. and Li, X. (2019) Exact Traveling Wave Solutions to Higher Order Nonlinear Equations. Journal of Ocean Engineering and Science, 4, 276-288. https://doi.org/10.1016/j.joes.2019.05.003

15. Durur, H. (2020) Different Types Analytic Solutions of the (1+1)-Dimensional Resonant Nonlinear Schrödinger’s Equation Using(G’/G)-Expansion Method. Modern Physics Letters B, 34, Article ID: 2050036. https://doi.org/10.1142/S0217984920500360

16. Yakup, Y. (2021) Optical Solitons with Biswas-Arshed Equation by F-Expansion Method. Optik, 227, Article ID: 165788. https://doi.org/10.1016/j.ijleo.2020.165788

17. Li, C.C., Chen, L.W. and Li, G.H. (2020) Optical Solitons of Space-Time Fractional Sasa-Satsuma Equation by F-Expansion Method. Optik, 224, Article ID: 165527. https://doi.org/10.1016/j.ijleo.2020.165527

18. Wen, X. (2010) Construction of New Exact Rational form Non-Travelling Wave Solutions to the (2+1)-Dimensional Generalized Broer-Kaup System. Applied Mathematics and Computation, 217, 1367-1375. https://doi.org/10.1016/j.amc.2009.05.058

19. Asíf, Y., Hulya, D., Hijaz, A., et al. (2020) Construction of Exact Traveling Wave Solutions of the Bogoyavlenskii Equation by (G’/G,1/G)-Expansion and (1/G’)-Expansion Techniques. Results in Physics, 19, Article ID: 103409. https://doi.org/10.1016/j.rinp.2020.103409

20. Yokuş, A. and Durur, H. (2019) Complex Hyperbolic Traveling Wave Solutions of Kuramoto-Sivashinsky Equation Using (1/G’) Expansion Method for Nonlinear Dynamic Theory. Balíkesir Üniversitesi Fen Bilimleri Enstitüsü Dergisi, 21, 590-599. https://doi.org/10.25092/baunfbed.631193

21. Durur, H. and Yokuş, A. (2019) (1/G’)-Açılım Metodunu Kullanarak Sawada-Kotera Denkleminin Hiperbolik Yürüyen Dalga Çözümleri. Afyon Kocatepe Üniversitesi Fen ve Mühendislik Bilimleri Dergisi, 19, 615-619. https://doi.org/10.35414/akufemubid.559048

22. Yokus, A., Durur, H., Ahmad, H. and Yao, S.-W. (2020) Construction of Different Types Analytic Solutions for the Zhiber-Shabat Equation. Mathematics, 8, 908. https://doi.org/10.3390/math8060908

23. Ghosh, U., Ali, M.R., Sarkar, S., et al. (2018) Formulation and Solution of Three Dimensional Space-Time Fractional KdV-Zakharov-Kuznetsov and Modified KdV-Zakharov-Kuznetsov Equation. International Journal of Applied Mathematics & Statistics, 57, 22-39.

24. Nur Alam, Md. and Ali Akbar, M. (2015) A Novel (G’/G)-Expansion Method for Solving the (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation in Mathematical Physics. International Journal Computing Science and Mathematics, 6, 404-415. https://doi.org/10.1504/IJCSM.2015.071812

25. Ma, W.X. (2011) Comment on the 3+1 Dimensional Kadomtsev-Petviashvili Equations. Communications in Nonlinear Science and Numerical Simulation, 16, 2663-2666. https://doi.org/10.1016/j.cnsns.2010.10.003

26. Zayed, E.M.E., Ibrahim, S.A.H. and Abdelaziz, M.A.M. (2012) Traveling Wave Solutions of the Nonlinear (3+1)-Dimensional Kadomtsev-Petviashvili Equation Using the Two Variables (G’/G, 1/G)-Expansion Method. Journal of Applied Mathematics, 2012, Article ID: 560531. https://doi.org/10.1155/2012/560531

27. Lu, D., Tariq, K.U., Osman, M.S., et al. (2019) New Analytical Wave Structures for the (3+1)-Dimensional Kadomtsev-Petviashvili and the Generalized Boussinesq Models and Their Applications. Results in Physics, 14, Article ID: 102491. https://doi.org/10.1016/j.rinp.2019.102491

28. 王子萌, 刘华楠. 疫情视域下社区治理多元化中的企业参与——以电商参与社区治理为例[J]. 城市管理与科技, 2021(6): 85-87.

29. 曾响铃. 超市守店等死, 还是抓住社区电商这根救命稻草? [J]. 商周刊, 2016(7): 8.

30. 刘春雄. 社区电商, 传统门店与新零售结合的最大赛道[J]. 销售与市场(管理版), 2019(1): 63-65.

31. 王宇飞, 蒋晓. 社会临场感视角下社区电商平台的体验设计研究[J]. 包装工程, 2020, 41(14): 222-227.

32. 李连英, 聂乐玲, 傅青. 不同类群消费者购买社区电商生鲜农产品意愿的差异性分析——基于南昌市578位消费者的实证[J]. 农林经济管理学报, 2020, 19(4): 457-463.

33. 简惠云, 杨欢. 社区电商技术特性对消费者购买意愿的影响[J]. 商业经济研究, 2020(23): 99-102.

34. 张应语, 张梦佳, 王强, 任莹, 马阳光, 马爽, 邵伟, 尹世久, 石忠国. 基于感知收益-感知风险框架的O2O模式下生鲜农产品购买意愿研究[J]. 中国软科学, 2015(6): 128-138.

35. 刘铭卿. 论电子商务信用法律机制之完善[J]. 东方法学, 2019(2): 151-160.

NOTES

^*通讯作者。

期刊菜单