Pure Mathematics
Vol.
13
No.
05
(
2023
), Article ID:
66409
,
9
pages
10.12677/PM.2023.135151
乘积图和F-Sum图的Steiner K-距离
胡玲莉1,颜娟2,陈娅红1,2*
1浙江理工大学理学院,浙江 杭州
2丽水学院数学与计算机学院,浙江 丽水
收稿日期:2023年4月23日;录用日期:2023年5月24日;发布日期:2023年5月31日

摘要
图的距离是图论中非常重要且基本的概念,是研究基于距离的图不变量的基础。Steiner距离是图论组合研究中的经典问题。本文运用Steiner树的定义证明了corona积的Steiner k-半径和cluster积的Steiner k-半径的上下界以及F-sum图的Steiner距离和Steiner k-直径的界。
关键词
Steiner距离,Steiner半径,Corona积,Cluster积,F-sum图

Steiner K-Distances in Graph Products and F-Sum Graphs
Lingli Hu1, Juan Yan2, Yahong Chen1,2*
1School of Science, Zhejiang Sci-Tech University, Hangzhou Zhejiang
2School of Mathematics and Computer Science, Lishui University, Lishui Zhejiang
Received: Apr. 23rd, 2023; accepted: May 24th, 2023; published: May 31st, 2023

ABSTRACT
Graph distance is a very important and basic concept in graph theory, which is the basis of studying graph invariants based on distance. Steiner distance is a classic problem in graph theory combinatorial research. This paper proves the upper and lower bounds of Steiner k-radius of corona product and cluster product and the bounds of Steiner distance and Steiner k-diameter of F-sum graphs by using the definition of Steiner tree.
Keywords:Steiner Distance, Steiner k-Radius, Corona Product, Cluster Product, F-Sum Graphs

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
图的Steiner问题是经典的组合优化问题。1989年,Chartrand等 [1] 引入了Steiner距离的概念并进行了初步的研究。Mao等 [2] 在2018年研究了笛卡尔积和字典序积的Steiner距离,并在Steiner距离的基础上给出了Steiner直径的上下界。2019年,Wang等 [3] 接着研究了阈值图、联结图、corona积、cluster积的Steiner距离和Steiner直径,引入了有关Steiner树的概念,运用Steiner树的结构特征证明了相关定理。其余有关Steiner距离的研究可参考Mao等 [4] [5] [6] ,Oellermann等 [7] 的工作。
乘积图的提出是基于这样一种思想,即利用乘积作为一种工具,将两个具有既定性质的已知图组合起来,得到一个新的图,该图继承了这两个图的性质。2009年,Eliasi等 [8] 引入了F-sum图的概念,研究了F-sum图的一般距离。本文对corona积,cluster积,F-sum图的Steiner半径、Steiner距离、Steiner直径进行研究。有关这三个乘积图 [9] - [18] 的一些参数及拓扑指数也得到了充分研究。
本文中所有图都是连通的简单无向图,且顶点个数至少为两个。假设G是一个连通图,顶点
,则
表示顶点
之间最短路的长度。令S是G的一个非空集合且
。点集S的Steiner距离
表示包含S的最小连通子图的边数,特别地,这个最小的连通子图一定是一颗树,令它为S-Steiner树。令k是一个整数且
,则图G中顶点v的Steiner k-离心率
被定义为
。此外,Steiner k-直径和Steiner k-半径的定义为
和
。连通图G的中心
是由
的顶点v诱导的子图,作为图中心的推广,连通图G的Steiner k-中心
是由最小Steiner k-离心率顶点导出的子图,其中
。
Corona积,Cluster积 [19] 和F-sum图 [8] 的定义如下:
定义1 Corona积
通过复制一个G,复制
个H,然后将复制的第i个H的每一个顶点与G的第 个顶点连接起来,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。
个顶点连接起来,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。
定义2 Cluster积
通过复制一个G,复制
个根图H,然后将复制的第i个根图H的根与G的第i个顶点相连,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。
定义3 F-sum图
的顶点集为
。
中的两个顶点分别为
和
,这两个顶点相邻当且仅当
且
或者
且
。
和T的定义如下:
:在图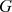 中的每条边上添加一个新的顶点,使得每条边都由长度为2的路替换所得的图。
中的每条边上添加一个新的顶点,使得每条边都由长度为2的路替换所得的图。
:在图G中的每条边上添加一个新的顶点,在图G的基础上,将每个新顶点连接到相应边的端点上所得的图。
:在图G中的每条边上添加一个新的顶点,将新顶点与相邻的顶点相连所得的图。
:将
和
结合所得的图。
其中,F代表图变换
和T中的一个。
下面给出两个重要的引理。
引理1 [3] G和H是两个连通图,其中
,
。令
是三个整数且
。S是
的顶点各不相同的集合,使得
。则有
,
其中
,
是
的最大子集使得对于任意的
都有
。
引理2 [3] 令点集S是Cluster积
的一个顶点各不相同的顶点集,如果存在
中的顶点在不同的
中,则
,
其中,当
,
时,有
。否则,令
,
,
是
的最大的子集使得对每一个
都有
。
2. 主要结果
2.1. Corona积和Cluster积的Steiner k-半径
定理1 令
是三个整数且
,连通图
分别有n和m个顶点。
如果
,那么
。
如果
,那么
。
如果
,那么
。
证明 以上三种情况的证明方法相同,这里仅考虑第二种情况。如果
,根据
的定义,可以发现存在一个顶点子集
,并且
使得
。令
,其中
。当
时,由引理1可得
(1)
另一方面,选择
使得
。则任意的S-Steiner树T一定包含
中的所有顶点(树T的大小至少是
),且令T的子树为
。对于
中的每一个顶点,至少需要一条边去连接它和
中的顶点,因此可以得到
(2)
由不等式(1)和(2),可以得出结论
。
定理2 令
和n三个正整数且
,令连通图
分别有
个顶点。
如果
,那么
。
如果
并且
,那么
。
如果
并且
,那么
。
如果
,那么
。
如果
,那么
。
证明 首先讨论
以上五种情况的上界。根据
的定义,可知存在一个顶点子集
且
,使得
。令
,
。其中
且
。由引理2可得
。
首先证明结论a)。如果
,则有
,
,并且
。因此
。
其次证明结论b)。如果
且
,则有
,并且
。因此
。
接着证明结论c)。如果
且
,可知
,
,并且
。因此
。
然后证明结论d)。如果
,可知
,
,并且
。因此
。
最后证明结论e)。显然可以得到
。
另一方面,由引理2可知
。且令
,
。对结论a)的下界进行证明,如果
,对于任意的S-Steiner树T一定包含
中的所有顶点(树T的大小至少是
),假设树T有子树
。对于每一个
中的顶点,需要至少一条边来连接它和
中的顶点,最终得到
。
结论b)和结论e)的证明与结论a)的证明类似。对于c)和d)中的情况,证明过程与其上界的证明完全一样。
推论1 假设
,
且
。对每一个
有
和
。如果
,则
;如果
,则
。
推论2 假设
,
且
。对每一个
有
和
。如果
,则
。
2.2. F-Sum图的Steiner距离
令G和H是两个连通图,并且
(
是图G的边数),k是一个整数。令
是F-sum图
的一个顶点各不相同的顶点集,其中F代表
和T中的其中一个。首先介绍几个参数:
• 令
是H的一个复制,其中
。
• 令
是集合
的(k-3)-重子集,其中
。令
是
中每个集合中不同顶点的个数,其中
。
• 令
是集合
的(k-3)-重子集,其中
。令
是
中每个集合中不同顶点的个数,其中
。
定理3 根据上面的定义,可以得到重集
和
。则
证明 根据对称性,这里只考虑
的情况。当
,假设
是
的r个复制,使得
,
。因此
。接下来,考虑三种情况:
情况1.
(S中的所以顶点都是实心的)且
。
由任意性,假设
,那么可以得到顶点
。
中存在一个大小为
的
-Steiner树,则在
中存在一个大小为
且包含顶点
的Steiner树,令这个Steiner树为
。
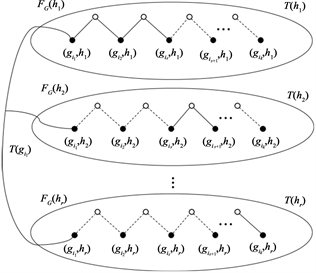
每一个
都有一个相对应的Steiner树
。所以
是一个大小为
且包含
中的顶点
的Steiner树。同样的,H也有一个大小为
的
-Steiner树。因此
包含
中的顶点
并且大小为
的Steiner树(见图1)。
如果
,则
的一个S-Steiner树是由边
组成。由b的定义可得
或
,则有
。
图1. S中的所以顶点都是实心的
如果
,其中
。若
,
的一个S-Steiner树是由边
组成,由b的定义可知
。若
或
,则
的一个S-Steiner 树是由边
组成,根据b的定义,可以得到
或者
,则
。
情况2.
(S中的所有顶点都是空心的)且
。
由任意性,假设
。则
,其中
。
对于每一个
都有与之相对应的Steiner树
。因此
是大小为
且包含
中k个顶点的Steiner树。同样的,图H有一个大小为
的
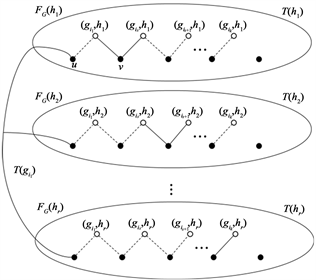
-Steiner树,因此
是一个大小为
且包含
中的r个顶点的Steiner树(见图2)。
图2. S中的所有顶点都是空心的
根据
的定义,对于任意的两个顶点
和
,且
。因此不能直接连接
中的
和
中的
。由任意性,假设
,
,即需要一条边去连接顶点u和
,那么
和
需要r条边去连接。
如果
,则
的一个S-Steiner树是由边
组成,根据b的定义可知
或
,则
。
如果
,其中
。若
,则
的一个S-Steiner树是由边
组成,由b的定义,可得
。若
或者
,则
的一个S-Steiner树是由边
组成,由b的定义可得
或
。即
。
情况3. 存在两个顶点
,
,其中顶点
,
。
每一个
都有与之相对应的Steiner树
。因此
是一个大小为
且包含
的顶点
的Steiner树。同样地,H有一个大小为
的
-Steiner树,因此
是一个大小为
且包含
中顶点
的Steiner树(见图3)。
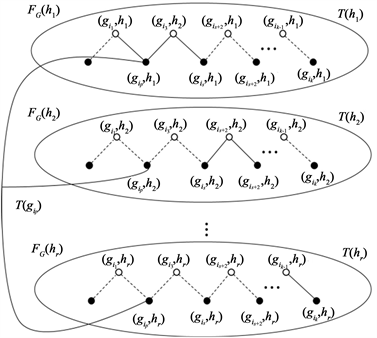
Figure 3. S contains two types of vertices
图3. S中包含两种类型的顶点
情况3的连接方式与情况1类似,即可证
。
现在来考虑下界。令
,其中
,
。根据图
的结构特征,显然
。
推论3 G和H是两个连通图,且
是一个整数。令
是
的一个顶点各不相同的集合。令
,
。如果
且
,则
,其中F代表
和T中的其中一个。
是H的一个复制,且
。
推论4 令G和H是两个阶数分别为
的连通图,令
是三个整数,并且
(
是图G的边数),
。假设
是H的一个复制, 可以知道
,F-sum图的Steiner直径如下
如果
,则
如果
,则
如果
,则
。
3. 结论
本文基于先前建立的关于图乘积的Steiner距离的结果,推广并证明了两个图的corona积和cluster积的Steiner半径,并用来自两个原始图的参数来表示它们。然后,在F-sum图中给出了Steiner距离的界,这反过来又有助于界定F-sum图的Steiner直径。以上得到的主要定理也可以应用于特殊图,并提供了简单的推论。
基金项目
国家自然科学基金项目(12201273);浙江省自然科学基金项目(LY21A010002)。
文章引用
胡玲莉,颜 娟,陈娅红. 乘积图和F-Sum图的Steiner K-距离
Steiner K-Distances in Graph Products and F-Sum Graphs[J]. 理论数学, 2023, 13(05): 1483-1491. https://doi.org/10.12677/PM.2023.135151
参考文献
- 1. Chartrand, G., Oellermann, O.R., Tian, S., et al. (1989) Steiner Distance in Graphs. Časopis Pro Pěstování Matematiky, 114, 399-410. https://doi.org/10.21136/CPM.1989.118395
- 2. Mao, Y.P., Cheng, E. and Zhao, W. (2017) Steiner Distance in Product Networks. Discrete Mathematics & Theoretical Computer Science, 20, Article No. 8.
- 3. Wang, Z., Mao, Y.P., Melekian, C., et al. (2019) Steiner Distance in Join, Corona, Cluster, and Threshold Graphs. Journal of Information Science and Engineering, 35, 721-735.
- 4. Mao, Y.P. (2017) The Steiner Diameter of a Graph. Bulletin of the Iranian Mathematical Society, 43, 439-454.
- 5. Mao, Y.P., Melekian, C. and Cheng, E. (2018) A Note on the Steiner (n-k)-Diameter of a Graph. International Journal of Computer Mathematics Computer Systems Theory, 3, 41-46. https://doi.org/10.1080/23799927.2018.1441186
- 6. Wang, Z., Mao, Y.P., Li, H.Z. and Ye, C.F. (2018) On the Steiner 4-Diameter of Graphs. Journal of Interconnection Networks, 18, Article ID: 1850002. https://doi.org/10.1142/S0219265918500020
- 7. Oellermann, O.R. and Tian, S. (2010) Steiner Centers in Graphs. Journal of Graph Theory, 14, 585-597.
https://doi.org/10.1002/jgt.3190140510
- 8. Eliasi, M. and Taeri, B. (2009) Four New Sums of Graphs and Their Wiener Indices. Discrete Applied Mathematics, 157, 794-803. https://doi.org/10.1016/j.dam.2008.07.001
- 9. Ashrafi, A.R., Hamzeh, A. and Hossein-Zadeh, S. (2011) Com-puting Zagreb, Hyper-Wiener and Degree-Distance Indices of Four New Sums of Graphs. Carpathian Journal of Mathematics, 27, 153-164.
https://doi.org/10.37193/CJM.2011.02.13
- 10. Kuziak, D., Yero, I.G. and Rodriguez-Velazquez, J.A. (2013) On the Strong Metric Dimension of Corona Product Graphs and Join Graphs. Discrete Applied Mathematics, 161, 1022-1027. https://doi.org/10.1016/j.dam.2012.10.009
- 11. Feng, M. and Wang, K. (2014) Identifying Codes of Corona Product Graphs. Discrete Applied Mathematics, 169, 88-96.
https://doi.org/10.1016/j.dam.2013.12.017
- 12. An, M., Xiong, L. and Das, K.C. (2014) Two Upper Bounds for the Degree Distances of Four Sums of Graphs. Filomat, 28, 579-590. https://doi.org/10.2298/FIL1403579A
- 13. Feng, M. and Kong, Q. (2018) On the Fractional Metric Dimension of Corona Product Graphs and Lexicographic Product Graphs. ARS Combinatoria: An Australian Canadian Journal of Combinatorics, 138, 249-260.
- 14. Aruvi, M., Joseph, J.M. and Ramganesh, E. (2021) Four New Sums of Second Hyper Zagreb Index Based on Cartesian Product. Communications in Mathematics and Applications, 12, 253-262.
- 15. Patil, S. and Basavanagoud, B. (2022) Generalized Four New Sums of Graphs and Their Zagreb Indices. Discrete Mathematics, Algorithms and Applications, 14, Article ID: 2150095. https://doi.org/10.1142/S1793830921500956
- 16. Agnes, V.S. (2015) Degree Distance and Gutman Index of Corona Product of Graphs. Transactions on Combinatorics, 4, 11-23.
- 17. 吕怡妃, 李俊, 黄达含, 陈娅红. F-sum图的零阶Randic指数与边度指数[J]. 丽水学院学报, 2019, 41(2): 1-12.
- 18. Liu, J.B., Imran, M., Baby, S., et al. (2022) Graph Indices for Cartesian Product of f-Sum of Connected Graphs. Combinatorial Chemistry & High Throughput Screening, 25, 528-535.
https://doi.org/10.2174/1386207324666210217143114
- 19. Mao, Y.P. and Furtula, B. (2021) Steiner Distance in Chemical Graph Theory. Match-Communications in Mathematical and in Computer Chemistry, 86, 211-287.
NOTES
*通讯作者。






 个顶点连接起来,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。
个顶点连接起来,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。 中的每条边上添加一个新的顶点,使得每条边都由长度为2的路替换所得的图。
中的每条边上添加一个新的顶点,使得每条边都由长度为2的路替换所得的图。