有限理性下不确定性模糊博弈强Berge均衡的稳定性及博弈的良定性 Stability of Strong Berge Equilibrium and Well-Posedness of Uncertain Fuzzy Game under Limited Rationality

doi:10.12677/ORF.2022.124147

Operations Research and Fuzziology
Vol. 12 No. 04 ( 2022 ), Article ID: 57717 , 8 pages
10.12677/ORF.2022.124147

有限理性下不确定性模糊博弈强Berge均衡的稳定性及博弈的良定性

毛浪，杨彦龙

●How to Cite this Article

贵州大学数学与统计学院，贵州贵阳

收稿日期：2022年10月6日；录用日期：2022年11月3日；发布日期：2022年11月11日

摘要

本文不仅考虑了现实经济中经济人的不完全理性以及来自外界环境的不确定参数的变化，而且还通过考虑博弈中的决策者策略集的不确定性，引入了模糊参数。首先，本文建立了有限理性下的不确定性模糊博弈模型，通过构造理性函数，并研究其性质，得到该博弈模型的模糊强Berge均衡的结构稳定性和鲁棒性结果。其次，研究了有限理性下的不确定性模糊博弈的良定性问题。

关键词

有限理性，不确定性，模糊博弈，良定

Stability of Strong Berge Equilibrium and Well-Posedness of Uncertain Fuzzy Game under Limited Rationality

Lang Mao, Yanlong Yang

School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou

Received: Oct. 6^th, 2022; accepted: Nov. 3^rd, 2022; published: Nov. 11^th, 2022

ABSTRACT

This paper not only considers the imperfect rationality of the economic man in the real economy and the change of uncertain parameters from the external environment, but also introduces fuzzy parameters by considering the uncertainty of the decision maker’s strategy set in the game. First of all, this paper establishes an uncertain fuzzy game model under bounded rationality. By constructing a rational function and studying its properties, we obtain the structural stability and robustness results of the fuzzy strong Berge equilibrium of the game model. Secondly, the well-posedness problem of uncertain fuzzy game under bounded rationality is studied.

Keywords:Limited Rationality, Uncertainty, Fuzzy Game, Well-Posedness

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

在现代经济学中，许多的经济模型都是建立在完全理性的基础之上，其中的“理性经济人”是指做出决策的人会在一定的约束条件之下最大化自身的利益，既是完全理性的。然而，这一假设与现实中的真实决策者们是不符的，也就是，在真实情况中，没有一个人可以做到完全理性的，故已有经济模型的应用受到了一定的限制。因此，在有限理性下研究经济或是博弈问题，不论是在理论和实践应用中都有重要的意义。

2001年，Anderlini和Canning [1] 构造了有限理性模型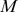，这是一类带有理性函数的“一般博弈”。2006年，学者Yu等 [2] 对模型 $M$ 进行了改进，减弱了相应的条件，使得模型的应用更为广泛。具体来说， $M = (Λ, X, F, R), Λ$ 是参数空间，每个 $λ \in Λ$ 是一个博弈， $X$ 是行为空间，每个 $x \in X$ 是一个策略， $F : Λ \times X \to P_{0} (X)$ 是可行映射，而由 $F$ 诱导出行为映射 $f : Λ \to P {}_{0}{(X)}$ ，其中 $\forall λ \in Λ$ ， $f (λ) = {x \in X : x \in F (λ, x)}$ ，集值映射 $f$ 的图 $g r a p h (f) = {(λ, x) \in Λ \times X : x \in f (λ)}$ ， $Φ : g r a p h (f) \to R_{+}$ 是理性函数， $\forall λ \in Λ, \forall ε \geq 0, E (λ, x) = {x \in f (λ) : R (λ, x) \leq ε}$ 定义为博弈的 $ε -$ 近似解集，特别地， $E (λ, x) = E (λ, 0)$ 定义为博弈的平衡点集，而 $R (λ, 0) = 0$ 当且仅当 $x \in E (λ)$ 。之后，Yu等将改进的有限理性模型应用到多目标博弈 [3]。对于有限理性模型博弈更多的研究可见 [4] [5] [6] [7]。

另一方面，在实际的情况中，因为信息的不完备性会导致一些不确定的变化参数存在，例如Larbani 和Lebbah [8] 指出，在经济中的不确定参数可能由于信息的不完备或者天气、温度等大自然因素，在工业中的不确定参数的影响可能来自于测量仪器的误差。对于博弈论的均衡求解问题实际上也是一个决策问题，所以对于不确定参数的考虑是必要的。Zhukovskii [9] 引入了不确定非合作博弈的NS均衡概念。此后，国内外许多学者就不确定下的博弈问题展开了大量的研究，具体可见文献 [10] - [15]。为了将有限理性引入到不确定性博弈中，陆和邬 [16] 研究了不确定下的有限理性非合作博弈，并研究了模型的良定性问题。王 [17] 给出了有限理性下最一般不确定下博弈的NS均衡的稳定性分析，进一步，作为扩展，还研究了有限理性下广义不确定性的广义博弈NS均衡的稳定性。

1965年，Zadeh [18] 发表的《模糊集理论》为之后的模糊数学研究提供了系统的理论基础。模糊集理论已经应用到许多领域，如不动点理论、变分不等式和博弈论等。1992年，Billot [19] 将模糊行为和微观经济学结合起来研究模糊博弈，证明了模糊经济平衡点的存在性。Kim和Lee [20] 提出了模糊抽象经济学和模糊均衡的概念，并利用模糊映射概念下的连续选择定理证明了均衡点的存在性。此后，国内外许多学者围绕着模糊博弈做了深入的研究，可见文 [21] - [26]。

受以上研究的启发，本文希望将模糊参数引入到不确定性下的有限理性博弈模型中，研究在有限理性下的不确定模糊博弈均衡的稳定性。首先，本文建立了不确定下模糊博弈的有限理性模型。其次，研究了其强Berge均衡解的稳定性。最后，给出了不确定下模糊博弈的有限理性模型的良定性结论。

2. 预备知识

文献 [2] 给出了模型 $M$ 鲁棒性和结构稳定性的定义及两者等价的结论。

定义2.1模型 $M = (Λ, X, F, R), Λ$ 在 $λ \in Λ$ 对 $ε -$ 近似解集是鲁棒地，如果 $\forall δ > 0, \exists \bar{ε} > 0$ ，有 $ε < \bar{ε}, d (λ, λ^{'}) < \bar{ε}, H (E (λ^{'}, ε), E (λ)) < δ$ 。称模型 $M$ 在 $λ \in Λ$ 是结构稳定地，如果集值映射 $E : Λ \to P_{0} (X)$ 关于 $λ \in Λ$ 是连续地。

引理2.1对于模型 $M$ ，设 $(Λ, ρ)$ 是一个完备度量空间， $(X, d)$ 为一度量空间， $f : Λ \to P {}_{0}{(X)}$ 是uso的，且 $\forall λ \in Λ$ ， $f (λ)$ 是非空紧集， $Φ : g r a p h (f) \to R_{+}$ 是lsc的，且 $\forall λ \in Λ, E (λ) \neq \emptyset$ ，那么

1) 平衡映射 $E : Λ \to P {}_{0}{(X)}$ 在 $Λ$ 上是usco的；

2) 存在 $Λ$ 中的一个稠密剩余集 $Q$ ，使得 $\forall λ \in Q$ ， $M$ 在 $λ$ 是结构稳定的；

3) 如果 $M$ 在 $λ \in Λ$ 是结构稳定的，则 $M$ 在 $λ \in Λ$ 对 $ε -$ 近似解集必是鲁棒的，从而 $\forall λ \in Q, M$ 在 $λ \in Λ$ 对 $ε -$ 近似解集必是鲁棒的；

4) $\forall λ \in Q, \forall λ_{n} \to λ, \forall ε_{n} \to ε$ ，有 $H (E (λ^{'}, ε), E (λ)) \to 0$ ；

5) 如果 $E (λ)$ 是单点集，则 $M$ 在 $λ \in Λ$ 是结构稳定的，在 $λ \in Λ$ 对 $ε -$ 近似解集是鲁棒的。

在 [27]，Yu给出了如下的定义和定理，并就良定性之间的关系给出了相关的引理。

设 $Λ$ 和 $X$ 都是度量空间， $λ \in Λ$

定义2.2如果 $\forall λ_{n} \in Λ$ ， $λ_{n} \to λ$ ， $\forall x_{n} \in E (λ_{n}, ε_{n})$ ，其中 $ε_{n} \to 0$ ，必存在 ${x_{n}}$ 的子序列 ${x_{n_{k}}}$ ，使 $x_{n_{k}} \to x \in E (λ)$ ，则称问题 $λ$ 是广义良定的，简记为G-wp；如果 $E (λ) = {x}$ （单点集）， $\forall λ_{n} \in Λ$ ， $λ_{n} \to λ$ ， $\forall x_{n} \in E (λ_{n}, ε_{n})$ ，其中 $ε_{n} \to 0$ ，必有 $x_{n} \to x$ ，则称问题 $λ$ 是良定的，简记为wp。

定义2.3如果 $\forall x_{n} \in E (λ, ε_{n})$ ，其中 $ε_{n} \to 0$ ，必存在 ${x_{n}}$ 的子序列 ${x_{n_{k}}}$ ，使 $x_{n_{k}} \to x \in E (λ)$ ，则称问题 $λ$ 是广义Tykhonov良定的，简记为GT-wp；如果 $E (λ) = {x}$ （单点集）， $\forall x_{n} \in E (λ, ε_{n})$ ，其中 $ε_{n} \to 0$ ，必有 $x_{n} \to x$ ，则称问题 $λ$ 是Tykhonov良定的，简记为T-wp。

定义2.4如果 $\forall λ_{n} \in Λ$ ， $λ_{n} \to λ$ ， $\forall x_{n} \in E (λ_{n})$ ，必存在 ${x_{n}}$ 的子序列 ${x_{n_{k}}}$ ，使 $x_{n_{k}} \to x \in E (λ)$ ，则称问题 $λ$ 是广义Hadamard良定的，简记为GH-wp；如果 $E (λ) = {x}$ （单点集）， $\forall λ_{n} \in Λ$ ， $λ_{n} \to λ$ ， $\forall x_{n} \in E (λ_{n})$ ，必有 $x_{n} \to x$ ，则称问题 $λ$ 是Hadamard良定的，简记为H-wp。

定理2.1给定有限理性模型 $M = (Λ, X, f, ϕ)$ ， $λ \in Λ$ ，如果

1) $f : Λ \to 2^{X}$ 在 $λ$ 上是上半连续的且 $f (λ)$ 是非空紧集；

2) $ϕ : Λ \times X \to R$ 满足当 $x \in f (λ)$ 时 $ϕ (λ, x) \geq 0$ 且在 $(λ, x)$ 是下半连续的，则

a) 问题 $λ$ 是G-wp；

b) 如果 $E (λ) = {x}$ （单点集），则问题 $λ$ 必是wp。

引理2.2 a) 如果问题 $λ \in Λ$ 是G-wp，则 $λ$ 是GT-wp又是GH-wp；

b) 如果问题 $λ \in Λ$ 是wp，则 $λ$ 是T-wp又是H-wp。

引入本文中所需要的关于模糊映射相关定义 [28]。

设 $M$ 和 $N$ 是两个Hausdorff拓扑向量空间， $R, S$ 分别是是 $M$ 和 $N$ 两个非空凸子集。定义模糊映射 $P : R \to F (S)$ ，其中 $F (S)$ 表示在 $S$ 上的所有模糊集的集合。对于每一个 $r \in R, P (r)$ 是 $F (S)$ 的一个模糊集(可以写为 $P_{r}$ )。 $P_{r} (s)$ 表示在 $P_{r}$ 里 $s$ 的隶属度。令 $A$ 属于 $F (S)$ 和 $α \in [0, 1]$ ，用 $A_{α}$ 表示 $A$ 的 $α -$ 截集，具体表示为 $A_{α} = {s \in S : A (s) \geq α}$ 。

定义2.5设 $R$ 和 $S$ 是两个Hausdorff拓扑向量空间， $B \subset R$ 是一个非空集。一个模糊映射 $P : B \to F (S)$ 被称为凸的，如果对于每个 $r \in B$ ， $P_{r}$ 是凸的。即对于任意 $s, t \in S$ 和 $λ \in [0, 1]$ ，有

$P_{r} (λ s + (1 - λ) t) \geq \min {P_{r} (s), P_{r} (t)}$

3. 主要结果

不确定下广义模糊博弈 $Γ = {(X_{i}, u_{i}, G_{i}, g_{i}, Y)}_{i \in I}$ 定义如下： $I = {1 \dots, n}$ 表示局中人构成的集合， $X_{i}$ 为局中人 $i$ 的策略集， $x \in X = \prod_{i = 1}^{n} X_{i}$ 为非合作博弈的局势， $x = (x_{i}, x_{- i}) \in X$ ， $Y$ 是不确定参数， $u = (u_{1}, u_{2}, \dots, u_{n})$ ， $u_{i} : X \times Y \to R$ 为第 $i$ 个局中人的支付函数， $G_{i} : X_{- i} \to F (X_{i})$ 是局中人 $i$ 模糊可行策略值映射， $g_{i} : X_{- i} \to [0, 1]$ 表示是对于局中人 $i$ 的可行度的可行函数。对于每个策略组合 $x_{- i}$ ，定义集值映射 $\tilde{G} : X_{- i} \to P_{0} (X_{i})$ ，表示由 $G_{i}$ 诱导出的集值映射，根据 $α -$ 截集的定义可表示为： ${\tilde{G}}_{i} (x_{- i}) = {(G_{i x_{- i}} (x_{i}))}_{g_{i} (x_{- i})} = {x_{i} \in X_{i} : G_{i x_{- i}} (x_{i}) \geq g_{i} (x_{- i})}$

定义3.1一个策略组合 $(\bar{x}, \bar{y}) \in X \times Y$ 被称为 ${(X_{i}, u_{i}, G_{i}, g_{i}, Y)}_{i \in I}$ 的模糊强Berge均衡，如果满足下列条件：

i) $\forall i \in I, {\bar{x}}_{i} \in {\tilde{G}}_{i} (x_{- i})$ ；

ii) $\forall j \in I - {i}, \forall x_{- i} \in {\tilde{G}}_{- i} ({\bar{x}}_{i}), u_{j} ({\bar{x}}_{i}, x_{- i}, y) \leq u_{j} ({\bar{x}}_{i}, {\bar{x}}_{- i}, \bar{y})$ ；

iii) $\forall y \in Y, u (\bar{x}, y) - u (\bar{x}, \bar{y}) \notin int R_{+}^{n}$ 。

注3.1条件(i) (ii)说明 $(\bar{x}, \bar{y})$ 是不确定下广义模糊博弈 $Γ = {(X_{i}, u_{i}, G_{i}, g_{i}, Y)}_{i \in I}$ 的模糊强Berge均衡。条件(iii)说明 $\bar{y}$ 是多目标问题 $(Y, u (\bar{x}, y))$ 的弱Pareto有效解，即所有局中人对不确定参数 $y$ 均持乐观主义态度。

注3.2如果 $Y = \emptyset$ 或 $Y = {y}$ 且 $F (X_{i})$ 不再是模糊集，则不确定广义模糊非合作博弈变为经典广义非合作博弈，其余情况类似。

假设 $X, Y$ 都是紧度量空间，设

$Λ = {\begin{cases} λ = {(u_{i}, X_{i}, G_{i}, g_{i}, Y)}_{i \in I}, G_{i} 是上半连续的且是凸值的, g_{i} 是下半连续的; \\ u_{i} : X \times Y \to R 连续；对于 \forall x_{i} \in X_{i}, \forall y \in Y, u_{- i} \to u_{- i} (x_{i}, u_{- i}, y) 是拟凹的； \\ \forall x \in X, y \to u (x, y) 是 R_{+}^{n} - 拟凹的； \forall (x, y) \in X \times Y, Γ^{1} (x, y) \neq \emptyset; \\ \sum_{i \in I, x \in X, y \in Y} | f_{i} (x, y) | < \infty; \\ 存在 (\bar{x}, \bar{y}) \in X \times Y ，使得 \\ \forall i \in I, {\bar{x}}_{i} \in {\tilde{G}}_{i} (x_{- i}) \\ \forall j \in I - {i}, \forall x_{- i} \in {\tilde{G}}_{- i} ({\bar{x}}_{i}), u_{j} ({\bar{x}}_{i}, x_{- i}, y) \leq u_{j} ({\bar{x}}_{i}, {\bar{x}}_{- i}, \bar{y}) \\ \forall y \in Y, u (\bar{x}, y) - u (\bar{x}, \bar{y}) \notin int R_{+}^{n} \end{cases}}$

对于任意 $λ_{1} = {(X_{i}, u_{i}^{1}, G_{i}^{1}, g_{i}^{1}, Y)}_{i \in I}$ 和 $λ_{2} = {(X_{i}, u_{i}^{2}, G_{i}^{2}, g_{i}^{2}, Y)}_{i \in I}$ ，定义距离

$ρ (φ_{1}, φ_{2}) = \sup_{x \in X, y \in Y} \sum_{i \in I} | u_{i}^{1} (x, y) - u_{i}^{2} (x, y) | + \sup_{x \in X, y \in Y} \sum_{i \in I} | G_{i}^{1} (x_{- i}) - G_{i}^{2} (x_{- i}) | + \sup_{x \in X, y \in Y} \sum_{i \in I} | g_{i}^{1} (x_{- i}) - g_{i}^{2} (x_{- i}) |$

定理3.1 $(Λ, λ)$ 是一个完备度量空间。

证明明显， $(Λ, λ)$ 是一个度量空间，下面证明 $(Λ, λ)$ 是完备的。设 $λ_{m} = {(X_{i}, u_{i}^{m}, G_{i}^{m}, g_{i}^{m}, Y)}_{i \in I}$ 是 $Λ$ 中的任意柯西列。那么，对任意的 $ε > 0$ ，存在 $N = N (ε) > 0$ ，使得当任意 $n, m > N$ ，有 $\begin{array}{l} ρ (φ_{n}, φ_{m}) = \sup_{x \in X, y \in Y} \sum_{i \in I} | u_{i}^{n} (x, y) - u_{i}^{m} (x, y) | + \sup_{x \in X, y \in Y} \sum_{i \in I} | G_{i}^{n} (x_{- i}) - G_{i}^{m} (x_{- i}) | + \\ \sup_{x \in X, y \in Y} \sum_{i \in I} | g_{i}^{n} (x_{- i}) - g_{i}^{m} (x_{- i}) | < \frac{ε}{3} + \frac{ε}{3} + \frac{ε}{3} < ε \end{array}$

因此，对于每一个固定的 $i$ ，当 $n, m > N$ 时，有

$| u_{i}^{n} (x, y) - u_{i}^{m} (x, y) | < \frac{ε}{3}$ (1)

$| G_{i}^{n} (x, y) - G_{i}^{m} (x, y) | < \frac{ε}{3}$ (2)

$| g_{i}^{n} (x, y) - g_{i}^{m} (x, y) | < \frac{ε}{3}$ (3)

即序列 $u_{i}^{k}, k = 1, 2, \dots$ 是柯西列，因此存在 $u_{i}$ ，使得 $u_{i}^{m} \to u_{i} (m \to \infty)$ 。下面证明 $u_{i} \in Λ$ 。在(1)式中令 $m \to \infty$ ，得到对一切 $m > N$ ，有

$| u_{i}^{n} (x, y) - u_{i} (x, y) | < \frac{ε}{3}$ (4)

又因为 $u_{i}^{n} \in Λ$ ，所以存在实数 $K_{n}$ ，使得对所有 $i$ ， $| u_{i}^{n} | < K_{n}$ 成立。因此 $| u_{i} | < | u_{i} - u_{i}^{n} | + u_{i}^{n} \leq ε + K_{n} < \infty$ 。固定 $\forall m > N$ ， $\forall (x, y) \in X \times Y$ ，因为 $u_{i}^{n} (x, y)$ 在 $X \times Y$ 上是连续的，即对于 $\forall ε > 0, \exists δ > 0$ ，当 $| (x, y) - (x^{'}, y^{'}) | < δ$ 时，有

$| u_{i}^{n} (x, y) - u_{i}^{n} (x^{'}, y^{'}) | < \frac{ε}{3}$ (5)

则有(4) (5)可得 $| u_{i} (x, y) - u_{i} (x^{'}, y^{'}) | < ε$ ，所以 $u_{i}$ 在 $X \times Y$ 上时连续的。其次，容易证明存在 $G_{i} : X_{- i} \times X_{i} \to [0, 1]$ 和 $g_{i} : X_{- i} \to [0, 1]$ 使得 $\lim_{n \to \infty} G_{i x_{- i}}^{n} (x_{i}) = G_{i x_{- i}} (x_{i})$ 和 $\lim_{n \to \infty} g_{i}^{n} (x_{- i}) = g_{i} (x_{- i})$ 。容易证明 $G_{i}$ 是一个上半连续映射且是凸值的在 $X_{- i}$ 上和 $g_{i}$ 是一个下半连续映射在 $X_{- i}$ 上。因为 $w_{- i} \to u_{- i}^{n} (x_{i}, w_{- i}, y)$ 在 $X_{- i}$ 上是拟凹的，既对于任意 $w_{- i}^{1}, w_{- i}^{2} \in X_{- i}, λ \in (0, 1)$ ，可有 $u_{- i}^{n} (x_{i}, λ w_{- i}^{1} + (1 - λ) w_{- i}^{2}, y) \geq \min {u_{- i}^{n} (x_{i}, w_{- i}^{1}, y), u_{- i}^{n} (x_{i}, w_{- i}^{2}, y)}$ ，自然有

$\begin{array}{l} u_{- i} (x_{i}, λ w_{- i}^{1} + (1 - λ) w_{- i}^{2}, y) > u_{- i}^{n} (x_{i}, λ w_{- i}^{1} + (1 - λ) w_{- i}^{2}, y) - ε \\ \geq \min {u_{- i}^{n} (x_{i}, w_{- i}^{1}, y), f_{- i}^{n} (x_{i}, w_{- i}^{2}, y)} - ε \\ \geq \min {u_{- i} (x_{i}, w_{- i}^{1}, y), u_{- i}^{n} (x_{i}, w_{- i}^{2}, y)} - 2 ε \\ \geq \min {u_{- i} (x_{i}, w_{- i}^{1}, y), u_{- i}^{n} (x_{i}, w_{- i}^{2}, y)} \end{array}$

则 $w_{- i} \to u_{- i} (x_{i}, w_{- i}, y)$ 在 $X_{- i}$ 上是拟凹的。最后得到 $λ = {(u_{i}, X_{i}, G_{i}, g_{i}, Y)}_{i \in I} \in Λ$ 。因此 $(Λ, λ)$ 是完备的。

接下来，构造不确定下广义模糊博弈的有限理性抽象模型 $M = (Λ, X, Y, F, R)$ ，其中 $λ \in Λ$ 分别定义理性函数 $R : Λ \times X \times Y \to R_{+}$ 和解集映射 $E : Λ \to P_{0} (X \times Y)$ 如下：

$F (λ, x, y) = \prod_{i = 1}^{n} G_{- i} (x_{i}) \times Y$

$R (λ, x, y) = \max_{i \in I, j \in I - {i}} \max_{u_{- i} \in {\tilde{G}}_{- i} (x_{i})} [u_{j} (x_{i}, u_{- i}, y) - u_{j} (x, y)] + \max_{\forall v \in y} \max_{‖ z ‖ = 1, z \in R_{+}^{n}} 〈 z, u (x, y) - u (x, v) 〉$

$E (λ) = {\begin{cases} \forall j \in I - {i}, \forall x_{- i} \in {\tilde{G}}_{- i} ({\bar{x}}_{i}), u_{j} ({\bar{x}}_{i}, x_{- i}, y) \leq u_{j} ({\bar{x}}_{i}, {\bar{x}}_{- i}, \bar{y}); \\ \forall y \in Y, u (\bar{x}, y) - u (\bar{x}, \bar{y}) \notin int R_{+}^{n} \end{cases}}$

$E (λ)$ 表示博弈 $λ$ 的所有模糊强Berge均衡点，由空间 $Λ$ 的定义可知 $E (λ) \neq \emptyset$ 。

定理3.2 1) $\forall λ \in Λ, \forall (x, y) \in f (λ), R (λ, x, y) \geq 0$ ；

2) $\forall λ \in Λ, \forall (x, y) \in f (λ), R (λ, x, y) = 0$ 当且仅当 $(x, y) \in E (λ)$ 。

定理3.3 $R (λ, x, y)$ 在 $(λ, x, y)$ 是连续的。

上述的定理证明类似于文献 [17] 中的引理4.1和引理4.2的证明。

综上可得，引理2.1的假设条件全部成立，因此其结论(1)~(5)也全都成立。既可得如下结论

定理3.4 1) 模糊强Berge均衡集值映射 $E : Λ \to P_{0} (X \times Y)$ 是上半连续的；

2) 存在一个稠密剩余集 $Q \in Λ$ ，对 $\forall λ \in Q, M = (Λ, X, Y, F, R)$ 在 $Q \in Λ$ 是结构稳定的；

3) 如果 $M = (Λ, X, Y, F, R)$ 在 $Q \in Λ$ 是结果稳定的，则 $M = (Λ, X, Y, F, R)$ 在 $Q \in Λ$ 对 $ε -$ 均衡解集是鲁棒的，从而 $M$ 在 $Q \in Λ$ 对 $ε -$ 均衡解集是鲁棒的；

4) 对 $\forall λ \in Q,$ Math_273#，有 $H (E (λ^{'}, ε), E (λ)) \to 0$ ；

5) 对 $\forall λ \in Q,$ 若 $E (λ)$ 为单点集，则 $M = (Λ, X, Y, F, R)$ 在 $Q \in Λ$ 是结构稳定的，而且对 $ε -$ 均衡解集也是鲁棒的。

定理3.5 i) 对 $\forall λ \in Λ$ ，不确定下广义模糊博弈是G-wp，从而也是GT-wp和GH-wp；

ii) 如果 $E (λ) = {x}$ （单点集）， $λ \in Λ$ ，则不确定下广义模糊博弈是WP，从而也是T-wp和H-wp。

证明i) 由于 $f$ 是连续的且对 $\forall λ \in Λ, f (λ)$ 是非空紧集， $R (λ, x, y)$ 在 $(λ, x, y)$ 是下半连续的，满足定理2.1的条件，所有对 $\forall λ \in Λ$ ，不确定下广义模糊博弈G-wp，再由引理2.2可知，不确定下广义模糊博弈也是GT-wp和GH-wp。

ii) 同i)的证明，满足定理的条件，再由引理2.2可以推出不确定下广义模糊博弈是WP，从而也是T-wp和H-wp。

4. 总结

本文研究了不确定性广义模糊博弈的有限理性模型模糊强Berge均衡的稳定性，同时给出了该博弈模型的相应良定结论。本文扩展了不确定性 $n$ 人非合作博弈的有限理性模型，引入了模糊集值映射，具有更强的理论价值和实践意义。

基金项目

国家自然科学基金项目(71961003)；贵州省科技厅联合基金项目(黔科合LH字[2017]7223)；贵州大学博士基金(贵大人基合字(2019)49)。

文章引用

毛浪,杨彦龙. 有限理性下不确定性模糊博弈强Berge均衡的稳定性及博弈的良定性
Stability of Strong Berge Equilibrium and Well-Posedness of Uncertain Fuzzy Game under Limited Rationality[J]. 运筹与模糊学, 2022, 12(04): 1392-1399. https://doi.org/10.12677/ORF.2022.124147

参考文献

1. Anderlini, L. and Canning, D. (2001) Structural Stability Implies Robustness to Bounded Rationality. Journal of Economic Theory, 101, 395-422. https://ideas.repec.org/a/eee/jetheo/v101y2001i2p395-422.html

2. Chao, Y. and Jian, Y. (2006) On Structural Stability and Robustness to Bounded Rationality. Nonlinear Analysis: Theory, Methods & Applications, 65, 583-592. https://www.sciencedirect.com/science/article/abs/pii/S0362546X05008394

3. Chao, Y. and Jian, Y. (2007) Bounded Rationality in Multi-Objective Games. Nonlinear Analysis Theory Methods & Applications, 67, 930-937. https://www.sciencedirect.com/science/article/abs/pii/S0362546X0600366X

4. 俞建. 几类考虑有限理性平衡问题解的稳定性[J]. 系统科学与数学, 2009, 29(7): 999-1008. http://www.cqvip.com/QK/71135X/201107/31185773.html

5. Yu, J., Yang, Z. and Wang, N.F. (2016) Further Results on Structural Stability and Robustness to Bounded Rationality. Journal of Mathematical Economics, 67, 49-53. https://ideas.repec.org/a/eee/mateco/v67y2016icp49-53.html

6. 俞建. 有限理性与博弈论中平衡点集的稳定性[M]. 北京: 科学出版社, 2017.

7. Miyazaki, Y. and Azuma, H. (2013) (λ, ϵ)-Stable Model and Essential Equilibria. Mathematical Social Sciences, 65, 85-91. https://www.sciencedirect.com/science/article/pii/S0165489612000807

8. Larbani, M. and Lebbah, H. (1999) A Concept of Equilibrium for a Game under Uncertainty. European Journal of Operational Research, 117, 145-156. https://ideas.repec.org/a/eee/ejores/v117y1999i1p145-156.html

9. Zhukovskii, V.I. and Chikrii, A.A. (1994) Linear Quadratic Differential Games. Naoukova Doumka, Kiev.

10. 张会娟, 张强. 不确定性下非合作博弈强 Nash 均衡的存在性[J]. 控制与决策, 2010(8): 1251-1254. http://www.cnki.com.cn/Article/CJFDTotal-KZYC201008027.htm

11. 张会娟, 张强. 不确定性下非合作博弈简单Berge均衡的存在性[J]. 系统工程理论与实践, 2010, 30(9): 1630-1635. http://www.cnki.com.cn/Article/CJFDTotal-XTLL201009015.htm

12. 杨哲, 蒲勇健. 广义不确定性下广义博弈中NS均衡的存在性[J]. 中国管理科学, 2013, 21(5): 165-171. http://www.cnki.com.cn/Article/CJFDTotal-ZGGK201305021.htm

13. 杨哲. 广义不确定性下非合作博弈中Berge-NS均衡的存在性[J]. 系统科学与数学, 2015, 35(9): 1073-1080. http://www.cnki.com.cn/Article/CJFDTotal-STYS201509008.htm

14. 邓喜才, 向淑文, 左羽. 不确定性下强Berge均衡的存在性[J]. 运筹学学报, 2013, 17(3): 101-107. http://www.cnki.com.cn/Article/CJFDTotal-YCXX201303011.htm

15. 邓喜才, 向淑文. 不确定下广义博弈强Berge均衡的存在性[J]. 应用数学学报, 2015, 38(2): 200-211. http://www.cnki.com.cn/Article/CJFDTotal-YYSU201502002.htm

16. 陆辰超, 邬冬华. 不确定性下非合作博弈的有限理性模型及良定性[J]. 应用数学与计算数学学报, 2016, 30(3): 339-348. http://www.cnki.com.cn/Article/CJFDTotal-YONG201603003.htm

17. 王能发. 有限理性下不确定性博弈均衡的稳定性[J]. 应用数学学报, 2017, 40(4): 562-572. http://www.cnki.com.cn/Article/CJFDTotal-YYSU201704008.htm

18. Zadeh, L.A. (1965) Fuzzy Sets. Infor-mation and Control, 8, 338-353. https://www.sciencedirect.com/science/article/pii/S001999586590241X

19. Billot, A. (1992) Economic Theory of Fuzzy Equilibria. Springer-Verlag, Heidelberg. https://linkspringer.53yu.com/book/10.1007/978-3-642-79949-5

20. Kim, W.K. and Lee, K.H. (2001) General-ized Fuzzy Games and Fuzzy Equilibria. Fuzzy Sets and Systems, 122, 293-301. https://www.sciencedirect.com/science/article/abs/pii/S0165011400000737

21. Yang, Z. and Wang, A. (2018) Existence and Stability of the α-Core for Fuzzy Games. Fuzzy Sets and Systems, 341, 59-68. https://www.sciencedirect.com/science/article/pii/S0165011417302300

22. Zhe, Y. (2020) A Coalitional Exten-sion of Generalized Fuzzy Games. Fuzzy Sets and Systems, 383, 68-79. https://www.sciencedirect.com/science/article/pii/S0165011418303981

23. Van Hung, N., Tam, V.M., O’Regan, D., et al. (2020) A New Class of Generalized Multiobjective Games in Bounded Rationality with Fuzzy Mappings: Structural (λ, ε)-Stability and (λ, ε)-Robustness to ε-Equilibria. Journal of Computational and Applied Mathematics, 372, Article ID: 112735. https://www.sciencedirect.com/science/article/pii/S0377042720300261

24. Wang, X. and Teo, K.L. (2022) Generalized Nash Equilibrium Problem over a Fuzzy Strategy Set. Fuzzy Sets and Systems, 434, 172-184. https://www.sciencedirect.com/science/article/pii/S0165011421002323

25. Zhou, L., Jia, W. and Liu, L. (2021) Essential Stability of Fuzzy Equilibria for Generalized Multiobjective Games with Fuzzy Constraint Mappings. Fuzzy Sets and Systems, 447, 113-122. https://www.sciencedirect.com/science/article/pii/S0165011421004280

26. Liu, J. and Yu, G. (2022) Fuzzy Kakutani-Fan-Glicksberg Fixed Point Theorem and Existence of Nash Equilibria for Fuzzy Games. Fuzzy Sets and Systems, 447, 100-112. https://www.sciencedirect.com/science/article/pii/S0165011422000409

27. 俞建. 关于良定问题[J]. 应用数学学报, 2011, 34(6): 1007-1022. http://www.cnki.com.cn/Article/CJFDTotal-YYSU201106006.htm

28. Aliprantis, C.D. and Border, K.C. (2006) Infinite Dimensional Analysis. Springer-Verlag, New York. https://linkspringer.53yu.com/book/10.1007/3-540-29587-9

期刊菜单