Advances in Applied Mathematics
Vol.
11
No.
05
(
2022
), Article ID:
51540
,
12
pages
10.12677/AAM.2022.115284
群、环、域的理论研究与实际应用
王秋艳,何伟奇,晋子钰,何依凡,张妍
辽宁师范大学数学学院,辽宁 大连
收稿日期:2022年4月20日;录用日期:2022年5月15日;发布日期:2022年5月23日

摘要
群、环和域是近世代数里重要的代数系统,为了增强学习者对于它们之间的联系和应用的理解,我们做以具体的总结和深入研究。本文首先介绍群、环、域产生与发展的过程,其次绘制了具体的群环域关系分析图,然后总结了与之相关定理及命题,最后分析了群论在密码学、图形的对称变换、分子结构及物理中的应用。
关键词
群,环,域

Theoretical Research and Practical Application of Groups, Rings and Fields
Qiuyan Wang, Weiqi He, Ziyu Jin, Yifan He, Yan Zhang
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Apr. 20th, 2022; accepted: May 15th, 2022; published: May 23rd, 2022

ABSTRACT
Groups, rings and fields are important algebraic systems in Modern Algebra. In order to enhance learners’ understanding of the relationship and application between them, we make a specific summary and in-depth research. This paper first introduces the emergence and development of groups, rings and fields, then draws a specific analysis diagram of the relationship between groups, rings and fields, then summarizes the related theorems and propositions, and finally analyzes the application of group theory in cryptography, symmetrical transformation of graphics, molecular structure and physics.
Keywords:Group, Ring, Field

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 群、环、域产生与发展的过程
群的概念来源于对多项式方程的研究,由伽罗瓦在19世纪30年代开创,他用伽罗瓦群的理论,解决了五次方程根式求解问题。在此之前柯西,阿贝尔等人也对群论作出了贡献。在得到来自其他领域如数论和几何学的贡献之后,群概念在1870年左右形成并牢固建立。
在研究当时,代数学的中心问题即五次及五次以上的一元多项式方程是否可用根式求解的问题时,经由拉格朗日、鲁菲尼、阿贝尔和伽罗瓦引入和发展,n个元的一些置换所构成的置换群得以诞生,并被有效地运用,从而彻底解决了这个中心问题。置换群是最终产生和形成抽象群的第一个主要的来源。
在数论中,拉格朗日和高斯研究过,由具有同一判别式D的二次型类,即 ,其中 为整数, 取整数值,且 为固定值,对于两个型的“复合”乘法构成一个交换群。戴德金于1858年和克罗内克于1870年在其代数数论的研究中也引进了有限交换群以至有限群。这些是导致抽象群论产生的第二个主要来源。
在若尔当的专著影响下,克莱因于1872年在其著名的埃尔朗根纲领中指出,几何的分类可以通过无限连续变换群来进行。克莱因和庞加莱在对“自守函数”的研究中曾用到其他类型的无限群(即离散群或不连续群)。在1870年前后,索菲斯·李开始研究连续变换群即解析变换李群,用来阐明微分方程的解,并将它们分类。无限变换群的理论成为导致抽象群论产生的第三个主要来源。
19世纪80年代,综合上述三个主要来源,数学家们终于成功地概括出抽象群论的公理系统,大约在1890年得到公认。
时至今日,群的概念已经普遍地被认为是数学及其许多应用中最基本的概念之一。它不但渗透到诸如几何学、代数拓扑学、函数论、泛函分析及其他许多数学分支中而起着重要的作用,还形成了一些新学科如拓扑群、李群、代数群、算术群等,它们还具有与群结构相联系的其他结构如拓扑、解析流形、代数簇等,并在结晶学、理论物理、量子化学以至(代数)编码学、自动机理论等方面,都有重要的应用。作为推广“群”的概念的产物:半群和幺半群理论及对计算机科学和对算子理论的应用,也有很大的发展。群论的计算机方法和程序的研究,已在迅速地发展。
环论的发展可追溯到19世纪关于实数域的扩张及其分类的研究。
环的概念原始雏型是整数集合。它与域不同之处在于对于乘法不一定有逆元素。抽象环论的概念来源一方面是数论,整数的推广——代数整数具有整数的许多性质,也有许多不足之处,比如唯一素因子分解定理不一定成立,这导致理想数概念的产生。戴德金在1871年将理想数抽象化成“理想”概念,它是代数整数环中的一些特殊的子环。这开始了理想理论的研究,在诺特把环公理化之后,理想理论被纳入环论中去。
环的概念的另一来源是19世纪对数系的各种推广,这最初可追溯到1843年哈密顿关于四元数的发现。他的目的是为了扩张用处很大的复数。它是第一个“超复数系”也是第一个乘法不交换的线性结合代数。它可以看成是实数域上的四元代数。不久之后凯莱得到八元数,它的乘法不仅不交换,而且连结合律也不满足,它可以看成是第一个线性非结合代数。其后各种“超复数”相继出现。
域的概念最初被阿贝尔和伽罗瓦隐含地用于他们各自对方程的可解性的工作上。早在19世纪初,伽罗瓦在研究代数方程的著作里就出现了域的概念的萌芽,后来戴德金和克罗内克在不同背景下也提出了域的概念。系统研究域的理论始于韦伯,而域的公理系统是迪克森和亨廷顿分别于1903和1905年独立创立的。在韦伯等人的影响下,施泰尼茨对抽象域进行了系统研究,于1910年发表论文“域的代数理论”,对域论本身以及相关科学的发展产生重大影响。
目前,域论发展前景十分广阔,其中有限域的性质可以构造出各种对称性质的组合结构,如正交拉丁方,平衡区组设计等,这些组合结构有效的应用于试验设计,通信系统等许多实际领域中,随着计算机技术蓬勃发展,有限域理论已经成为广大工程技术人员不可或缺的数学工具。
2. 群、环、域的相关命题及条件
在研究相关命题及条件之前本文根据参考文献《近世代数基础》、《近世代数》(详见参考文献 [1] [2])先梳理群、环、域的定义与性质之间的关系,如图1。
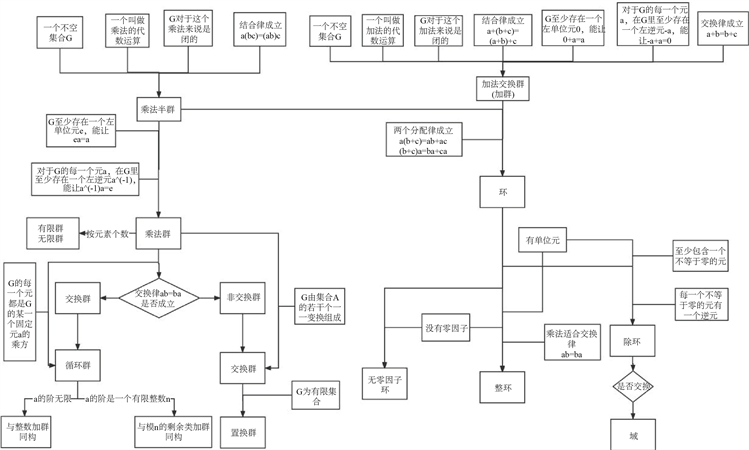
Figure 1. Group, ring and fields diagram
图1. 群、环、域关系图
2.1. 群的相关命题
我们研究群是遵循着从具体到抽象的方法进行的。根据凯莱定理,可以将群分为两种具体的群:变换群、置换群。而直接研究抽象群,就是研究它的分类、数量、结构。循环群就是一类完全在我们掌握下的群。
下面给出循环群的几个相关命题:
命题2.1.1 一个循环群一定是交换群。
反之,命题1的逆命题不成立。交换群不一定是循环群,如克莱因四元群。
例2.1.1 设群 ,用运算表来表示 的代数运算。
根据运算表不难发现, 是交换群。而 ,,,。故 不是循环群,交换群不一定是循环群。
命题2.1.2 若G是循环群,并且G与 同态,则 也是循环群。
命题2.1.3 阶是素数的群一定是循环群。
反之,命题2.1.3的逆命题不成立。循环群的阶不一定是素数。
例2.1.2 设群 ,。G是循环群,但G的阶为6,不是素数。
命题2.1.4循环群的子群也是循环群。
2.2. 环的相关命题
命题2.2.1在一个没有零因子的环里两个消去律都成立:
反过来,在一个环里如果有一个消去律成立,那么这个环没有零因子。
命题2.2.2 假定一个环R对于加法来说作成一个循环群,则R是交换环。
命题2.2.3二项式定理 在交换环中成立。
命题2.2.4 一个至少有两个元而且没有零因子的有限环是一个除环。
反之不真,即只有零理想和单位理想的环未必是除环。
例2.2.1 ,我们说 只有零理想和单位理想。
设N是 的一个理想, ,
不失一般性,假设 。那么
,易知
,所以
但 不是除环,因为 没有逆。
命题2.2.5 在一个没有零因子的环R里所有不等于零的元对于加法来说阶都是一样的。
命题2.2.6 如果无零因子环R的特征是有限整数n,那么n是一个素数。
命题2.2.7 若是存在一个环R到 的满射,使得环R与 对于一对加法以及一对乘法来说都同态,那么 也是一个环。
反之不真,即存在一个非空集合R到一个环 的满射,使得R与 对于一对加法以及一对乘法来说都同态,R未必是一个环。
例2.2.2 ,其运算为:加法: ,乘法: ;
是环。令 , 则 是R到 的满射,且R与 同态。但R不是环。
命题2.2.8 假定两个环R和 同态。那么,R的零元的象是 的零元,的R元a的负元的象是a的象的负元。并且,假如R是交换环,那么 也是交换环;假如R有单位元1,那么 也有单位元 ,而且 是1的象。
说明:交换律和单位元在环同态之下能“保持”过去,但有无零因子这一性质却不一定。
例2.2.3 设R是整数环, 是模n的剩余类环,那么R到 的映射
显然是R到 的一个同态满射。我们知道,R是没有零因子的,但当n不是素数时, 有零因子。即R没有零因子时,与R同态的 可以有。
例2.2.4 。对于代数运算
来说,R显然作成一个环。现在我们用 来表示整数环,那么
显然是一个R到 的同态满射。R的零元是 ,而
所以R有零因子。但 没有零因子。即R有零因子时,与R同态的 可以没有(详见参考文献 [3])。
命题2.2.9 假定R同 是两个环,并且 。那么,若R是整环, 也是整环;R是除环, 也是除环;R是域, 也是域。
命题2.2.10假定S是环R的一个子环,S在R里的补足集合(这就是所有不属于S的R的元作成的集合)与另一个环 没有共同元,并且 。那么存在一个与R同构的环 ,而且 是 的子环。
命题2.2.11给了一个有单位元的交换环R,一定有R上的未定元x存在,因此也就有R上的多项式环 存在。
命题2.2.12一个除环R只有两个理想,就是零理想和单位理想(详见参考文献 [4])。
例2.2.5看整数环R。那么一个整数 ,1的所有倍数 作成一个理想。
例2.2.6看一个环R上的一元多项式环 。那么所有多项式
作成 的一个理想。
命题2.2.13假定R是一个环, 是它的一个理想, 是所有模 的剩余类作成的集合。那么 本身也是一个环,并且R与同态。
命题2.2.14假定R同 是两个环,并且R与 同态,那么这个同态满射的核 是R的一个理想,并且 。
命题2.2.15在环到环的一个同态满射之下,
i) R的一个子环S的象 是 的一个子环;
ii) R的一个理想 的象 是 的一个理想;
iii) 的一个子环 的逆象S是R的一个子环;
iv) 的一个理想 的逆象 是R的一个理想。
命题2.2.16假定R是一个有单位元的交换环, 是R的一个理想。 是一个域,当而且只当 是一个最大理想的时候。
例2.2.7我们看整数环R。我们说,由一个素数p所生成的主理想 是一个最大理想。因为:假定是 一个不等于 的R的理想,并且
那么 一定包含一个不能被p整除的整数q。由于p是素数,q与p互素,所有我们可以找到整数s和t,使得
但p也属于 ,而且 是理想,所以
,
例2.2.8 R是整数环, 是由素数p所生成的主理想。那么由上面例2.2.5, 是一个域。
2.3. 域的相关命题
由于域是交换单环,无真理想,因而域不能像群、环那样,通过对不变子群,商群或理想、商环来讨论。常用的方法是从已知域出发,研究它的扩域。
首先来看域的生成相关定理:
引理2.3.1 (域的生成定理引理) 假定 是环R的理想,剩余类环R/U除了零理想同单位理想以外不再有理想,当而且只当U是最大理想的时候。
引理2.3.2 (域的生成定理引理) 若有单位元( )的交换环R除了零理想同单位理想以外没有其他的理想,那么R一定是一个域。
定理2.3.1 (域的生成定理) 假定R是一个有单位元的交换环,U是R的一个理想,R/U是一个域,当而且仅当U是一个最大理想的时候。
其次来看商域的相关定理:
引理2.3.3 (商域引理1) 每一个没有零因子交换R都是一个域Q的子环。
引理2.3.4 (商域引理2) Q刚好是由所有元
所作成的,这里
定理2.3.2 (商域定理1) 假定R是一个有两个以上的元的环,F是一个包含R的域,那么F包含R的一个商域。
定理2.3.3 (商域定理2)同构的环的商域也同构,这样,抽象地来看,一个环最多只有一个商域。
接着分析域的特征及相关定理:
定义2.3.1 (域的特征定义) 假设p是最小的正整数,使得p个1相加等于0,那么p就称为域的特征。特别地,如果任何多个1相加都不是0,那么特征p就等于0。
定理2.3.4 如果域的特征不等于零,则其特征一定为素数。
证明:设域F的特征为p, 。如果p为合数,则存在 ,使得 ,则
而 和 都是域F中的一个元素,并且F中没有零因子。所以有 或 ,但这与p是F的特征的前提矛盾。所以p不是合数,p为素数。
定理2.3.5 设域F的特征为p,则对任意的 ,,则 的充要条件是: 。
证明:必要性显然成立。
充分性:令 ,则
因为 且F中没有零因子,所以 。
这与p是F的特征的前提矛盾。
然后分析有限域及相关定理:
定理2.3.6 有限域的阶只能是素数q的幂,并且对任何一个素数幂n都有一个阶为n的有限域,其中n为整数。
定理2.3.7 设 是一个q阶的有限域,则 对于乘法构成一个循环群(有限域的乘法群是一个循环群)。
证明:因为 是一个域,所以 对于乘法构成一个阶为 有限群。
令 则 ,则 ,,。所以 的阶为 。
设元素a的阶为 ,则 ,将 的解表示成集合 ,而在集合
中,由 可知,阶为d的元素个数为 。如果 中阶为d的元素,那么 ,所以 ,而 ,所以 ,所
以对所有能够整除 的整数d都有 ,所以 ,,所以 ,所以 是一个循环群。
定理2.3.8 如果有限域F的特征为p,那么F中元素的数目为p的方幂。
定理2.3.9 设p是任一素数而n是任一正整数,那么总存在着一个恰好 个元素的有限域。
定理2.3.10 任何无限域必定包含与有理数域同构的子域,而任何特征为p的有限域必定包含与 同构的子域。
再来研究扩域及相关定理:
定义2.3.2 设F是一个域,如果 是F的子域,则称F为 的扩域。
若 ,且 ,F的含 和 的最小子域记为 。
定理2.3.11 如果F是 的扩域,则 ,而且,F可作为 上的线性空间。
最后研究域的同构及相关定理:
定义2.3.3 如果在域F和K之间可以建立一个同态双射,那么我们说F和K同构。
定理2.3.12 设 和 是域, 是一个同构,那么 把 的0映射到 的0,把 的1映射到 的1,而且 ; 。
定理2.3.13 设 和 是域, 是一个同构,那么这两个域的特征一样。
证明:如果 特征为0,对任意正整数n, 。由定理2.3.4, ,所以对于任意正整数n,有 。于是 特征为0。
如果 特征为p, 。由定理1, ,所以 特征不为0,且是一个整除p的素数,于是 特征为p。
定理2.3.14 两个阶相同的域必然同构。
定理2.3.15 任意两个元素个数相同的有限域一定同构。
3. 群论的应用
3.1. 群论在密码中的应用
双钥密码体制的关键即为找到一个恰当的单向函数,而单向函数的定义应用到了近世代数中有关映射的内容。
定义3.1.1 一个可逆函数 ,若它满足:
1) 对所有 ,易于计算 。
2) 对“几乎所有 ”由 求x “极为困难”,以至于实际上不可能做到,则称f为一单向(One-way)函数。
定义中的“极为困难”是对现有的计算资源和算法而言。
例3.1.1 令 是在有限域 中的指数函数,其中p是大素数,即
式中, ,其逆运算是 中定义的对数运算 。
显然,由x求y是容易的,即使当p很大,例如 时也不难实现。为方便计算以下令 。所需的计算量为 次乘法,存储量为 bit,利用高速计算机由x计算 可在0.1毫秒内完成。但是相对于当前计算 中对数最好的算法,当 时,以计算指数一样快的计算机进行计算需时约1010.7秒(1年 = 107.5秒,故约为1600年!其中假定存储量的要求能够满足)。可见,当p很大时, 中的 是个单向函数。
3.2. 图形的对称变换群
定义3.2.1 使图形不变形地变到与他重合的变换称为这个图形的对称变换。
定义3.2.2 图形的一切对称变换关于变换的乘法构成群,称为这个图形的对称变换群。
例3.2.1 正三角形的对称变换群
设正三角形的三个顶点分别为1、2、3,如图2,显然,正三角形的每一个对称变换都导致正三角形的三个顶点的唯一一个置换。反之,由正三角形的三个顶点的任一置换都可得到正三角形的唯一一个对称变换,从而可用
表示正三角形的对称变换群。
其中 为恒等变换, 分别表示关于正三角形的三个对称轴的反射变换, 分别表示关于正三角形的中心按逆时针方向旋转120度、240度的旋转变换。

Figure 2. Regular triangle
图2. 正三角形
例3.2.2 正方形的对称变换群
正方形的四个顶点分别用1、2、3、4来表示,如图3。于是正方形的每一对变换可用一个4次置换来表示。显然,不同的对称变换的乘积对应的置换也不同,而对称变换的乘积对应了置换的乘积。这说明,正方形的对称变换群可用一置换群来表示。
容易看出,正方形的对称变换有两类:
第一类:绕中心的分别旋转90度,180度,270度,360度的旋转,这对应于置换
第二类:关于正方形的4条对称轴的反射,这对应于置换
所以,正方形的对称变换群由上述8个元素,这是四次对称群的一个子群。
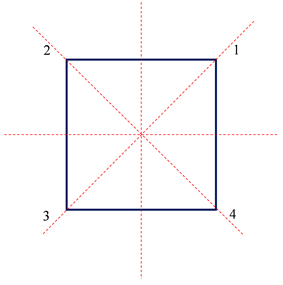
Figure 3. Square
图3. 正方形
3.3. 基于换位子的密钥交换协议(详见参考文献 [5])
定义3.3.1设 为群G的两个元素,称元素 为 的换位子。
定义3.3.2共轭问题是指是否存在算法来判断群G中给定的任意两个元素是共轭元素,两个元素 共轭是指存在G中的元素w,使得 成立。
定理3.3.1设公共信息为群G,两个系列 和 为群G的元素。用户A在 中选择一个私钥X,用户B在 中选择一个私钥Y。用户A将下列序列发送给用户B:
而用户B则将下列序列发送给用户A:
则用户A和用户B拥有公共的密钥 。
证不妨令 ,其中 ,则由共轭运算的基本特征有:
而表达式 ,,就是用户B发送给用户A的值,X又是A的私钥,从而他可以计算换位子 的值。同理,不妨令 ,其中 ,则:
而表达式 ,就是用户A发送给用户B的值, 又是B私钥Y的逆,从而用户B可以计算 。因此,用户A和用户B就具有了一个共享密钥。定理得证。
3.4. 群在分子结构的问题中的应用
在化学领域,已知分子包含的化学键与原子,能够利用群论知识快速地求解合成物的个数。以下面的问题为例说明群在应用中的重要地位。
设在苯环结构上的碳原子之间是由单双键交替连接的,在每个碳原子上结合CH3或H或NO2,问能够合成多少种不同的化合物?
首先我们把苯环连接键看成相同的。此时,我们可以将该问题转化为含有三种颜色的六个珠子的项链问题。对此,我们先引入利用群来求解项链问题的方法:
例3.4.1 用m颗n种颜色的珠子制作项链,能够设计出多少种不同的项链。(注:这里的“不同”是指两个项链无论怎样旋转与翻转都不能重合。)
解 用一个正m边形代表项链,它的每个顶点代表一颗珠子。沿逆时针方向对珠子进行标号,如图4所示。
利用乘法原理,有标号的项链有 。
但是这里包含了一些可以通过旋转一个角度或翻转180度使它们完全重合,而问题中需要的是无论怎么旋转或翻转都不能使它们重合的项链类型数。对于n,m小的情况可以用枚举法得到所有类型的项链,但是随着n,m的增加,用枚举法解决问题越来越难。所以采用群论这一最简单,最有效的方法。
但实际上苯环连接键是不同的,其单双键是交替的,故而在此基础上增加对旋转群的分析,由于两个分子重合时,必须经过旋转后键的重合,包含单键和双键。故该旋转群为G,同构于 。
又全部有标号的分子数是36。G作用于有标号的分子结构上的不动点数计算如表1所示。

Figure 4. Taking octagons as an example
图4. 以八边形为例
Table 1. Calculation of the number of fixed points acting on the labeled molecular structure
表1. 作用于有标号的分子结构上的不动点数计算
所以 ,即共可以形成138种不同的物质。
3.5. 群论在机器人中的应用(详见参考文献 [6])
在机器人领域,群论最初主要应用在机器人运动学的研究。随着研究的深入,从群论的角度将群论应用于机器人的装配、标定和控制。机器人的位置无论是用矢量表示,还是用旋量表示,或以四元数、双四元数等其他形式表示,其运动变换可以看作是群运算。由于连杆的内部结构在变换过程中保持不变,其变换可以看作欧氏群的一个子群。群中的变换包括旋转和平移两种。在机器人运动学中,若采用群描述机器人的运动,则表达式更简洁、更通用,便于符号推理,利用群论描述机器人运动还便于设计通用的机器人语言。在机器人操作中,操作对象通常是对称的或具有对称的特性,用一般的数学工具很难描述其相对位置,而用群可以很方便地描述其相对关系。特别是在装配任务中,当相互匹配的两个零件具有对称性时,它们有很多装配位置,这很难用一般的数学工具来描述,用群就可很容易地表示并进行推理。机器人在许多操作过程中具有非线性和非完整性,常用的线性控制不能满足其控制性能要求,人们开始用非线性系统的几何理论来解决,其状态变换是在流形上进行的,它使用的工具是李群和李代数,李群是连续群中重要的一种。
3.6. 群论在量子力学中的应用
群论是量子力学的基础。从群论的角度解决一些量子力学问题,主要包括哈密顿算符的对称性,矩阵元定理和选择定则。运用群论的方法研究量子系统的对称性,可以不通过求解运动方程得到系统许多普遍的精确的性质。
群论方法的特点在于,只要依据的对象的对称性质是严格的,则由它得出的结论必定是精确的、可靠的;特别适当研究者对研究对象不是很了解时,通过对其对称性的分析可以得出一些带普遍性的结论。
量子力学的基本问题是研究薛定谔方程的解:
但是,除了在极少数简单情况外,一般情况很难得到E及 的精确解。群论的方法可以通过找出哈密顿量H的对称性,预测能量E的简并情况。这便是群论在量子力学中的一种应用。
下面将简单讨论群论在量子力学中的具体应用实例。
例3.7.1 氢原子能级偶然简并的解释
由量子力学的薛定谔方程求解得到某一确定能级对于若干态矢量(或波函数),这种多个态矢量处于一个能级的现象称为“简并”。它表明原子的哈密顿量具有某种对称性。因原子核的库仑势具有球对称性,故一般多电子原子态矢量由三个量子数 描述(不计自旋)。能级 与量子数 有关简并度是 ;但是,对于氢原子(或类氢原子)同样情况简并度却高得多
氢原子的简并度高于一般原子的现象,成为“偶然简并”。传统量子力学除了说明量子数的意义之外,无法解释偶然简并现象。
随着群论的引入,偶然简并现象得到正确的解释。群论指出:多电子原子其哈密顿仅具球对称性,属于 群;氢原子(及类氢原子)哈密顿量除了几何对称性之外,还有更高的对称性(即內禀对称性),属于 群,故其简并度高于一般多电子原子。
4. 结论
群、环、域是近世代数中重要的代数系统,其产生和发展从19世纪30年代到现今具有深远的意义。本文首先对此进行了系统的介绍,体现了各个定义和理论的探究过程,为近世代数的学习提供了历史基础。其次,总结了群、环、域理论之间的关系图以及各部分的命题和条件,使得整体的群环域体系更加完整。目前群已经深入渗透到几何学、代数拓扑学、函数论、泛函分析及其他许多数学分支之中。最后,本文分别举例介绍了群论在密码学,图形对称变换,基于换位子的密钥交换协议,分子结构问题,机器人中的应用,从多个角度打开群论的研究大门。
文章引用
王秋艳,何伟奇,晋子钰,何依凡,张 妍. 群、环、域的理论研究与实际应用
Theoretical Research and Practical Application of Groups, Rings and Fields[J]. 应用数学进展, 2022, 11(05): 2682-2693. https://doi.org/10.12677/AAM.2022.115284
参考文献
- 1. 张禾瑞. 近世代数基础[M]. 北京: 高等教育出版社, 1978.
- 2. 任芳国. 近世代数[M]. 西安: 陕西师范大学出版总社, 2014.
- 3. 胡崇慧. 代数中的反例[M]. 西安: 陕西科学技术出版社, 1983.
- 4. 李秀云. 理想在环论中的作用[J]. 承德民族师专学报, 2001(2): 12-13.
- 5. 汤绍春. 由群论中换位子实现的密钥交换及其应用[J]. 韶关学院报, 2010, 31(9): 27-30.
- 6. 卢江舟, 熊有伦, 张启先. 群论及其在机器人装配中的应用[J]. 机器人, 1998(5): 76-81.
