Pure Mathematics
Vol.
09
No.
09
(
2019
), Article ID:
32935
,
21
pages
10.12677/PM.2019.99128
The Construction and the Mallat Algorithm of Biorthogonal Two Dimensional Four-Direction Multi-Wavelet with Dilation Factor a
Xu Zhang, Wanshe Li*
School of Mathematics and Information Science, Shaanxi Normal University, Xi’an Shaanxi

Received: Oct. 18th, 2019; accepted: Nov. 6th, 2019; published: Nov. 13th, 2019

ABSTRACT
Through the concept of two dimensional four-direction multi-scaling function and two dimensional four-direction multi-wavelet, the two dimensional four-direction orthogonal multi-wavelet with dilation factor two is generalized to two dimensional biorthogonal multi-wavelet with dilation factor a. Furthermore, the construction algorithm of two dimensional biorthogonal multi-scaling function and multi-wavelet with dilation factor a is given. Finally, the Mallat algorithm of two dimensional four-direction multi-wavelet with dilation factor a is studied.
Keywords:Two Dimensional Four-Direction Multi-Scaling Function, Two Dimensional Four-Direction Multi-Wavelet, Biorthogonality, Mallat Algorithm
a尺度二维四向双正交多小波的构造和Mallat算法
张旭,李万社*
陕西师范大学,数学与信息科学学院,陕西 西安

收稿日期:2019年10月18日;录用日期:2019年11月6日;发布日期:2019年11月13日

摘 要
通过二维四向多加细函数以及二维四向多小波的概念,推广二尺度二维四向正交多小波为a尺度二维四向双正交多小波,更进一步对于a尺度二维四向双正交多加细函数和多小波的构造算法做出了相应给出,最后研究了a尺度二维四向多小波的Mallat算法。
关键词 :二维四向多加细函数,二维四向多小波,双正交性,Mallat算法

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
小波分析是这些年来发展起来的一门新兴数学理论以及方法,在信号处理,语音处理,图像处理,数据压缩,微分方程求解,地震勘探等各个领域有着广泛的应用。Haar小波是同时具有正交性,对称性和紧支撑性的单小波,但是其它单小波并不能具有这样好的性质,所以人们引入了多小波。从带宽来看,二尺度小波高频端的带宽比较窄,那么从小波分析的效果来看二尺度小波效果相对比较差,所以人们提出了a尺度小波。双向小波的概念是杨守志等人首先提出的 [1],后来进一步得出了一系列好的理论和结果 [2] [3]。本文在引入二维四向多小波基础上,建立了a尺度二维四向多加细函数和a尺度二维四向多小波,给出了a尺度二维四向多加细函数和a尺度二维四向多小波的正交和双正交准则,以及它们的构造算法,最后讨论了a尺度二维四向多小波的分解与重构的Mallat算法。
2. 预备知识
先给出文章要提到的记号:
表示N维复欧几里德空间。
表示
阶单位矩阵,
表示
阶零矩阵,
表示向量或矩阵的转置,向量值函数信号空间
可以表示为
,(根据文献 [4] )对于
它的积分和Fourier变换分别定义为
和
若F和G都是一元函数空间,它们两个的基底分别为
和
,二元函数空间H表示为
是F和G的张量积空间,H的基底可以表示为
。
定义
的张量积空间为
,而
表示为由一元尺度函数
生成的一个正交多分辨分析。那么关于二元函数
,引入记号
。
二维四向加细尺度函数
基于双向尺度函数的概念,现在假设有
个双向尺度函数
,记
,那么通过
和
的张量积来构造二维四向多尺度函数。假设双向加细函数
和
都符合细分方程
设
,就能得出
从而根据适合的
,就有
令
,则
那么就可以有a尺度多小波细分方程
(1)
接下来对(1)式进行Fourier变换就可以有
(2)
其中
令
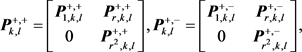
为双正,正负和双负矩阵符号。下面对(1)进行变形有
(3)
(4)
(5)
下面对(3)~(5)式都进行Fourier变换就有
(6)
(7)
(8)
根据(2)(6)~(8)式可以有,令
(9)
方程(2)有解,当且仅当式(9)有解。
设
(10)
则(9)式为
在频域里的a尺度加密方程,它的加细面具符号为
(11)
定义方程(1)的自相关矩阵符号
其中
下面引入变换算子
:
(12)
其中
是
的Laurent多项式,
由(12)式可知。
关于
和
可以有下面的引理。
引理1:矩阵符号
和变换算子
的定义如上,那么由Poisson求和公式可得
进一步,我们可以得出
是
相应于特征值为1的特征矩阵。
定理1:加细方程(1)有紧支撑解当且仅当它的面具符号满足下面情况之一
1)
2)
3)
4)
证明:根据文献 [5] [6] [7] [8],方程(10)存在紧支撑分布解当且仅当1是(11)式定义矩阵
的一个特征值,
的其他特征值的模都不大于1。另外,
的4个特征值分别是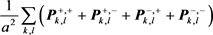 ,
, 以及
。定理易证。
,
, 以及
。定理易证。
定理2:若要
有紧支撑性,则要证明每个分量是紧支撑的。设
,其中
和
是双向细分函数满足
如果
和
是紧支撑的,那么可根据
和
的张量积生成二维四向加细函数
,,则有
证明:根据文献 [9] 中定理4可知。
3. a尺度二维四向多分辨分析
定义子空间序列
,
(13)
那么要产生在
中的一个多分辨分析
当且仅当(13)式里的
应当满足以下条件:
1)
;
2)
;
3)
;
4)
;
5) 存在
里的一个函数
,使得集合
是
的Riesz基,那么就有两个常数
,则对于系数向量序列
有
(14)
称式(14)为稳定性条件。
根据多重多分辨分析的性质
,可以定义:
则
同样可以构成
的Riesz基,有
因为
,并且
同样也可以构成
的Riesz基,故有
,从而使
满足(1)式。
定理3:如果尺度函数
符合多分辨分析,现定义
构成
的Riesz基。若存在函数集
构成
的Riesz基,那么
。
证明:由于
构成
的Riesz基,故存在两个常数
,对任意的
,有
所以对于所有的
,就有
对于
,,存在一个紧支撑连续函数
,使
。
若
是
的正交投影算子,则
,故
。
设
,则
其中
。所以,当
时
。同理,可以证明:
,,。又由于
所以
。根据
,可以知道
。
定理4:若
符合定义式(1),根据(13)式定义的
,若
满足1) 集合
是
的Riesz基;2) 对所有的
, 有界;3)
在
附近连续,
,那么
。
证明:由于
构成
的Riesz基,故存在两个常数
,对任意的
,有
所以对于所有的
,就有
对于 ,
,那么就有紧支撑连续函数
,使
。
,
,那么就有紧支撑连续函数
,使
。
若
是
的正交投影算子,则
。又因为
,则
进一步可以得到
其中
因为
,所以存在一个常数M,使
故
由以上的推导,可以得到
由于
有界且在
附近处连续且
,故当
时,以上不等式收敛于
从而
,所以
,因为
是任意小的,所以
,则说明
。
4. 双正交二维四向加细函数和小波
定理5:如果二维四向加细函数是正交的,那么应该满足下列等式
定理6:如果二维四向加细函数
和
是双正交的,那么应该满足下列等式
定理7:如果二维四向加细函数
和
是双正交的尺度函数,那么它的双正面具,正负面具和双负面具符号都应该满足
(15)
其中:
;
。
证明:由文献 [7] 的定理1以及本文定理5定理6正交双正交定义易证。
假设
和
是双正交二维四向加细函数,对任意的
,定义
,其中
是
在
中的正交补。那么当
时,就有
并且
,其中
,,,。
如果有r个小波函数
,则记
,则通过张量积的构造就有
和
,使得集合
和集合
构成
的一组双正交基,则
和
是与
和
对应的双正交二维四向多小波函数,应该满足
(16)
其中:
。
假如
是
对应的多小波函数,相应的
是
对应的多小波函数,那么就存在
,,, 和
,,,,满足
(17)
(18)
对(17)式和(18)式两边做Fourier变换
其中
为
的双正,正负,双负面具符号。
为
的双正,正负,双负面具符号。
定理8:若
和
是双正交二维四向多加细函数,
和
是相应的双正交二维四向多小波函数,则它们的面具符号满足
 (19)
(19)
 (20)
(20)
其中:
。
证明:根据(16)式的正交性易得。
5. 构造算法
定理9:如果
和
是双正交二维四向多加细函数,
和
是相应的双正交二维四向多小波函数,
和
是矩阵符号,构造
。函数
和
以
为周期,且满足
1)
2)
3)
4)
则
和
,产生一个双正交二维四向多细分函数
并满足
证明:将上面已经构造的
和
,代入(15)式化简可得。再令(11)式
,则化简
并求特征值可证得定理。
定理10:如果
和
是双正交二维四向多加细函数,
和
是相应的双正交二维四向多小波函数,
和
是面具符号,构造
。函数
, 和
以
为周期,且满足
1) 
2)
那么就可以得出
和
产生一个双正交二维四向多小波函数
并满足
证明:由于
, 和
, 的双正交性,可以将已构造的
和
,代入(16)式和(19)式化简可证得定理。
6. Mallat算法
如果
和
是双正交二维四向多加细函数,
和
是相应的双正交二维四向多小波函数,对于能量有限信号
在分辨率
下的近似函数
,则
可分解为
,则
,记
, 有
6.1. 分解算法
如果
在分辨率
下的近似函数为
,那么它可以进一步分解为
在
下的主要部分(通过低通滤波器得到)和细节部分(通过高通滤波器得到)。即分解算法要实现的目标就是:已知
,求
和
。
定理11:若
并且由(1)式和(17)式,我们可以得到下列分解公式
其中:
。
证明:因为
是
的标准正交基,所以就有
则根据(1)式和(20)式可以知道,
。同理可以证得:
故我们就可以得到
其它等式同理可证。
6.2. 重构算法
通过
在分辨率
下的主要部分和细节部分,来重构
在分辨率
下的主要部分,也即重构算法是分解算法的逆过程,那么要实现的目标就是:已知
和
求
。
定理12:若
并且由(1)式和(17)式,我们可以得到下列重构公式
证明:由于
而且
,类似可得
故我们可以证得
其它等式同理可证。
文章引用
张 旭,李万社. a尺度二维四向双正交多小波的构造和Mallat算法
The Construction and the Mallat Algorithm of Biorthogonal Two Dimensional Four-Direction Multi-Wavelet with Dilation Factor a[J]. 理论数学, 2019, 09(09): 1015-1035. https://doi.org/10.12677/PM.2019.99128
参考文献
- 1. 杨守志, 李尤发. 具有高阶逼近阶和正则性的双正交加细函数和双向小波[J]. 中国科学A辑: 数学, 2007, 37(7): 779-795.
- 2. 库福立, 王刚, 库媛. a尺度的二维四向小波问题[J]. 吉林大学学报: 理学版, 2013, 51(5): 763-782.
- 3. 李万社, 郝伟, 蒙少亭. a尺度正交双向小波的Mallat算法[J]. 陕西师范大学学报: 自然科学, 2010, 38(3): 1-5.
- 4. 陈江清, 程正兴, 杨守志. 向量值正交小波包[J]. 应用数学, 2005, 18(4): 505-515.
- 5. Yang, S.Z. (2006) Biorthogonal Two-Direction Refinable Function and Two Direction Wavelet. Applied Math and Computation, 182, 1717-1724. https://doi.org/10.1016/j.amc.2006.06.003
- 6. Yang, S.Z. and Li, Y.F. (2007) Two-Direction Refinable Function and Two-Direction Wavelet with Dilation Factor m. Applied Math and Computation, 188, 1908-1920. https://doi.org/10.1016/j.amc.2006.11.078
- 7. Xie, C.Z. (2008) Constrution of Biorthogonal Two-Direction Refinable Function and Two-Direction Wavelet with Dilation Factor m. Computers and Methematics with Application, 56, 1845-1851. https://doi.org/10.1016/j.camwa.2008.04.007
- 8. 杨守志, 程正兴. a尺度多重正交小波包[J]. 应用数学, 2000, 13(1): 61-65.
- 9. Yang, S.Z. and Xue, Y.M. (2009) Two-Direction Poly-Scale Refinability. Computers and Methematics with Application, 58, 119-127. https://doi.org/10.1016/j.camwa.2009.03.095







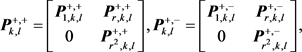
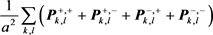 ,
, 以及
。定理易证。
,
, 以及
。定理易证。 ,
,那么就有紧支撑连续函数
,使
。
,
,那么就有紧支撑连续函数
,使
。 (19)
(19) (20)
(20)