一族链环的Alexander多项式 Alaxander Polynomials a Family of Links

doi:10.12677/AAM.2019.811201

Advances in Applied Mathematics
Vol. 08 No. 11 ( 2019 ), Article ID: 32891 , 6 pages
10.12677/AAM.2019.811201

Alaxander Polynomials a Family of Links

Wei Zheng

●How to Cite this Article

Liaoning Normal University, Dalian Liaoning

Received: Oct. 16^th, 2019; accepted: Nov. 4^th, 2019; published: Nov. 11^th, 2019

ABSTRACT

Pretzel link is a kind of special and simple link. This paper studies a kind of special directional Pretzel link $P (c_{1}, c_{2}, \dots, c_{n})$ , gives $P (c_{1}, c_{2}, \dots, c_{n})$ Seifert surface and the property of Seifert matrix, and finds the Alexander polynomial calculation formula of this family of Pretzel link.

Keywords:Pretzel Link, Seifertmatrix, Alexander Polynomial

一族链环的Alexander多项式

郑玮

辽宁师范大学，大连辽宁

收稿日期：2019年10月16日；录用日期：2019年11月4日；发布日期：2019年11月11日

摘要

排叉链环是一类既特殊又简单的链环，本文研究一类特殊的定向排叉链环 $P (c_{1}, c_{2}, \dots, c_{n})$ ，给出了 $P (c_{1}, c_{2}, \dots, c_{n})$ 的Seifert曲面以及Seifert矩阵的性质，找到这一族排叉链环的Alexander多项式的计算公式。

关键词 :排叉链环，Seifert矩阵，Alexander多项式

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

纽结理论是数学中拓扑学的一个分支，纽结的等价分类问题在纽结领域中十分重要。人们通过寻找纽结不变量来解决纽结的等价问题，常见的纽结不变量有三色性、交叉数、解结数、桥数、纽结多项式、纽结群等。本文研究一类特殊的排叉链环 $P (2 K_{1}, 2 K_{2}, \dots, 2 K_{n})$ ，通过选取适当的定向，进一步研究 $P (2 K_{1}, 2 K_{2}, \dots, 2 K_{n})$ 的Seifert曲面以及Seifert矩阵的性质，并给出这一类排叉链环的Alexander多项式的计算公式。

2. 预备知识

2.1. 纽结

把嵌入到三维欧式空间 $R^{3}$ 中或者球面 $S^{3}$ 中的单位圆周 $S^{1}$ 称为纽结，设K是 $S^{3}$ 中的简单闭曲线，且 $K ≅ S^{1}$ ，称K是一个纽结 [1]。若给定纽结一个方向便可得到一个定向纽结。

2.2. 投影图

选择一个恰当的平面，将三维空间中的纽结正则投影到平面上，且满足：只有有限多个交叉点；每个交叉点都是二重点；在每个二重点处，上下两线的投影都是互相穿越交叉的则称为纽结投影图。注意，平面的选择不同随之投影图不唯一。

2.3. 链环

将若干互不相交的圆周 $S_{i}^{1} (1 \leq i \leq n, n > 1)$ 嵌入到三维欧式空间 $R^{3}$ 中或者球面 $S^{3}$ 中，由这些圆周形成的空间图形称为链环，记为 $L = K_{1} \cup K_{2} \cup \dots \cup K_{n}$ 。其中 $K_{i} (i = 1, 2, \dots, n)$ 称为L的一个分支，n为链环的分支数.若通过合痕后所有的 $K_{i}$ 都是平凡纽结，则此时称L为平凡链环;若给定每个分支一个方向，便可得到一个定向链环。

2.4. Seifert曲面

设K是一个纽结，若S是以K为边界的曲面，则称S是K的Seifert曲面。

2.5. 交叉数

设K为 $R^{3}$ 中的一个纽结，在K的所有的正则投影图中包含交叉点最少的那个投影图上的交叉点数就称为K的交叉数，记作 $c (K)$ 。

2.6. Seifert矩阵

若 $v_{j k} = l k (a_{j}^{-}, a_{k})$ 是 $a_{j}^{-}, a_{k}$ 的交错数，记 $V = (v_{j k})$ 为K的Seifert矩阵。

设S是K的一个Seifert曲面 $e_{1}, e_{2}, \dots, e_{n - 1}$ 是 $π_{1} (S)$ 的一组生成元，在 $S^{3}$ 中取S的正则邻域 $N (S) = S \times [- 1, 1]$ 其中 $S = S \times {0}$ ，记 $e_{i}^{+} = e_{i} \times {1}$ ，则 $e_{1}^{+}, e_{2}^{+}, \dots, e_{n - 1}^{+}$ 是 $π_{1} (S \times {1})$ 的一组生成元。令 $v_{j k} = l k (a_{j}, a_{k}^{+})$ 是 $a_{j}, a_{k}^{+}$ 的交错数，记 $V = (v_{j k})$ 为K的Seifert矩阵 [2]。

2.7. 定理1

$V = (v_{j k})$ 为K的Seifert矩阵，那么 $A (t) = V^{T} - t V$ 就是K的Alexander矩阵，Alexander矩阵与Alexander多项式的关系是： $Δ (t) = \det A (t)$ [3]。

3. 定理证明

定理：当 $n \geq 3$ 时，则排叉链环 $P (2 K_{1}, 2 K_{2}, \dots, 2 K_{n})$ 的Alexander多项式为，

$\begin{matrix} \det A (t) \\ = {(1 - t)}^{n - 1} | \begin{matrix} K_{1} + K_{2} & - K_{1} & K_{1} & \dots & \dots & {(- 1)}^{n} K_{1} \\ K_{2} & K {}_{3} \\ K_{3} & K_{4} \\ ⋮ \\ ⋱ \\ K_{n - 2} & K_{n - 1} \\ K_{n - 1} & K_{n} \end{matrix} | \\ = {(1 - t)}^{n - 1} \sum_{i = 1}^{t} K_{1} K_{2} \dots {\bar{K}}_{i} \dots K_{n} \end{matrix}$

证明：如图1所示排叉链环 [4] $P (2 K_{1}, 2 K_{2}, \dots, 2 K_{n})$

Figure 1. Pretzel link

图1. 排叉链环

选定如图所示定向，对其进行如图特殊的定向，并找到其相应的Seifert曲面如图2所示。

Figure 2. Seifert surface

图2. Seifert曲面

从而找到Seifert曲面的生成元 $e_{1}, e_{2}, \dots, e_{n - 1}$ ，找到相邻两个生成元之间的交错数 [3]，如图3。

Figure 3. Generator of a seifert surface

图3. Seifert曲面的生成元

根据定理1我们可知 $V = | \begin{matrix} e_{1} e_{1}^{+} & e_{1} e_{2}^{+} & \dots & e_{1} e_{n}^{+} \\ e_{2} e_{1}^{+} & e_{2} e_{2}^{+} & \dots & e_{2} e_{n}^{+} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ e_{n} e_{1}^{+} & e_{n} e_{2}^{+} & \dots & e_{n} e_{n}^{+} \end{matrix} |$ 如图4所示我们可以找到 $e_{1} e_{1}^{+}$ 的交叉数为 $K_{1} + K_{2}$ 。

Figure 4. The winding method of $e_{1} e_{1}^{+}$

图4. $e_{1} e_{1}^{+}$ 的缠绕方式

$e_{1} e_{2}^{+}$ 的缠绕方式如图5所示所以交叉数为 $K_{2}$

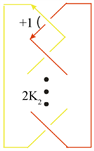
Figure 5. The winding method of $e_{1} e_{2}^{+}$

图5. $e_{1} e_{2}^{+}$ 的缠绕方式

$e_{2} e_{1}^{+}$ 的缠绕方式如图6所示，所以交叉数为 $K_{2}$

Figure 6. The winding method of $e_{2} e_{1}^{+}$

图6. $e_{2} e_{1}^{+}$ 的缠绕方式

用相同的方法我们可以找到V中的其他元素。由定理2，找到Seifert曲面对应的Seifert矩阵

$V = [\begin{matrix} K_{1} + K_{2} & K_{2} \\ K_{2} & K_{2} + K_{3} & K_{3} \\ ⋱ \\ K_{n - 2} & K_{n - 2} + K_{n - 1} & K_{n - 1} \\ K_{n - 1} & K_{n - 1} + K_{n} \end{matrix}]$

再由定理1 $A (t) = V^{T} - t V$ 写出排叉链环 $P (2 K_{1}, 2 K_{2}, \dots, 2 K_{n})$ 的Alexander矩阵

$\begin{matrix} A (t) = V^{T} - t V \\ = {(1 - t)}^{n - 1} [\begin{matrix} K_{1} + K_{2} & K_{2} \\ K_{2} & K_{2} + K_{3} & K_{3} \\ ⋱ \\ K_{n - 2} & K_{n - 2} + K_{n - 1} & K_{n - 1} \\ K_{n - 1} & K_{n - 1} + K_{n} \end{matrix}] \end{matrix}$

$\det A (t) = {(1 - t)}^{n - 1} | \begin{matrix} K_{1} + K_{2} & K_{2} \\ K_{2} & K_{2} + K {}_{3} & K_{3} \\ ⋱ \\ K_{n - 2} & K_{n - 2} + K_{n - 1} & K_{n - 1} \\ K_{n - 1} & K_{n - 1} + K_{n} \end{matrix} |$

将 $\det A (t)$ 的第一列 $\times (- 1)$ 加到第二列，再将变形后的第二列 $\times (- 1)$ 加到第三列，按照此方法一直到 $n - 1$ 列，即得到：

$\det A (t) = {(1 - t)}^{n - 1} | \begin{matrix} K_{1} + K_{2} & - K_{1} & K_{1} & \dots & \dots & {(- 1)}^{n} K_{1} \\ K_{2} & K {}_{3} \\ K_{3} & K_{4} \\ _{} & ⋮ \\ ⋱ \\ K_{n - 2} & K_{n - 1} \\ K_{n - 1} & K_{n} \end{matrix} |$

当 $n = 3$ 时 $\det A (t) = {(1 - t)}^{2} | \begin{matrix} K_{1} + K_{2} & K_{2} \\ K_{2} & K_{2} + K_{3} \end{matrix} | = K_{2} K_{3} + K_{1} K_{3} + K_{1} K_{2}$ 显然成立。

令 $n = N$ 则有

$\det A (t) = {(1 - t)}^{N - 1} | \begin{matrix} K_{1} + K_{2} & - K_{1} & K_{1} & \dots & \dots & {(- 1)}^{N} K_{1} \\ K_{2} & K {}_{3} \\ K_{3} & K_{4} \\ ⋮ \\ ⋱ \\ K_{N - 2} & K_{N - 1} \\ K_{N - 1} & K_{N} \end{matrix} | = \sum_{i = 1}^{n} K_{1} K_{2} \dots {\bar{K}}_{i} \dots K_{N}$

当 $n = N + 1$ 时按第n行展开

$\begin{matrix} \det A (t) = {(1 - t)}^{N} | \begin{matrix} K_{1} + K_{2} & - K_{1} & K_{1} & \dots & \dots & {(- 1)}^{N + 1} K_{1} \\ K_{2} & K {}_{3} \\ K_{3} & K_{4} \\ ⋮ \\ ⋱ \\ K_{N - 1} & K_{N} \\ K_{N} & K_{N + 1} \end{matrix} | \\ = {(1 - t)}^{N} K_{N + 1} (\sum_{i = 1}^{N} K_{1} K_{2} \dots {\bar{K}}_{i} \dots K_{N}) \\ + {(1 - t)}^{N} {(- 1)}^{2 N - 1} K_{N} | \begin{matrix} K_{1} + K_{2} & - K_{1} & {(- 1)}^{N + 1} K_{1} \\ K_{2} & K_{3} \\ ⋮ \\ ⋱ & ⋮ \\ K_{N - 2} & K_{N - 1} \\ K_{N - 1} & 0 \end{matrix} | \\ = {(1 - t)}^{N} K_{N + 1} (\sum_{i = 1}^{N} K_{1} K_{2} \dots {\bar{K}}_{i} \dots K_{N}) + {(1 - t)}^{N} K_{1} K_{2} \dots K_{N} \\ = {(1 - t)}^{N} \sum_{i = 1}^{N + 1} K_{1} K_{2} \dots {\bar{K}}_{i} \dots K_{N + 1} \end{matrix}$

即得证。

文章引用

郑玮. 一族链环的Alexander多项式
Alaxander Polynomials a Family of Links[J]. 应用数学进展, 2019, 08(11): 1716-1721. https://doi.org/10.12677/AAM.2019.811201

参考文献

1. Adams, C.C. (2004) The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. The American Mathematical Society, Providence.

2. Collins, J. (2016) An algorithm for Computing the Seifert Matrix of a Link from a Braid Representation. Ensaios Matemáticos, 30, 246-262.

3. Kauffman, L.H. and Lopes, P. (2017) Infinitely Many Prime Knots with the Same Alexander Invariants. Journal of Knot Theory and Its Ramifications, 26, Article ID: 1743009.
https://doi.org/10.1142/S021821651743009X

4. Landvoy, R.A. (1998) The Jones Polynomial of Pretzel Knots and Links. Topology and Its Applications, 83, 135-147.
https://doi.org/10.1016/S0166-8641(97)00100-4

期刊菜单