分数阶四翼混沌系统滑模同步 Sliding Mode Synchronization of a Four-Wing Fractional-Order Chaotic Systems

doi:10.12677/AAM.2020.910196

Advances in Applied Mathematics
Vol. 09 No. 10 ( 2020 ), Article ID: 38063 , 8 pages
10.12677/AAM.2020.910196

分数阶四翼混沌系统滑模同步

时文俊，丁艳风，蔡国梁

●How to Cite this Article

郑州升达经贸管理学院，应用数学研究所，河南郑州

收稿日期：2020年9月26日；录用日期：2020年10月8日；发布日期：2020年10月15日

摘要

根据分数阶微积分的相关理论，采用自适应滑模控制方法，研究了不确定分数阶四翼混沌系统的滑模错位同步控制问题和比例积分滑模同步问题，给出了驱动–响应系统取得同步的充分条件，结果表明：选取适当的控制律和滑模面，分数阶四翼系统的驱动–响应系统取得混沌同步。

关键词

分数阶，四翼混沌系统，积分滑模，错位同步

Sliding Mode Synchronization of a Four-Wing Fractional-Order Chaotic Systems

Wenjun Shi, Yanfeng Ding, Guoliang Cai

Institute of Applied Mathematics, Zhengzhou Shengda University of Economics, Business & Management, Zhengzhou Henan

Received: Sep. 26^th, 2020; accepted: Oct. 8^th, 2020; published: Oct. 15^th, 2020

ABSTRACT

The problem of sliding model dislocated synchronization and sliding mode synchronization with proportional integral of a class of uncertainty four-wing fractional-order chaotic systems is studied using self-adaptive sliding mode control approach based on fractional-order calculus theory. The sufficient conditions are arrived for the fractional-order systems sliding mode synchronization. The research conclusion illustrated the master-slave systems of four-wing fractional-order chaotic systems is sliding mode chaos synchronization under proper controllers and sliding mode surface.

Keywords:Fractional-Order, Four-Wing Chaotic Systems, Integral Sliding Model, Dislocated Synchronization

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

混沌同步一直是非线性科学的研究热点方向，它在经济金融系统、保密通信和信息安全等领域有着很大应用前景。作为整数阶系统推广之一的分数阶混沌系统，它具有比整数阶更复杂的动力学特征，能够更加真实地模拟自然界中的实际问题。所以，分数阶混沌系统的理论研究备受学者关注。孙宁等 [1] 围绕驱动系统和响应系统的投影同步问题，提出了一类不确定分数阶系统的滑模投影同步方法，也拓展了混沌同步方法；胡满峰等 [2] 讨论了Lorenz混沌系统的非线性反馈错位同步问题；J Sun等 [3] 研究了一类非线性实混沌系统和一类非线性复混沌系统的完全错位同步；Y Xu [4] 等研究了超混沌系统吕系统的错位同步；余明哲等 [5] 利用自适应滑模同步控制方法，提出了一类分数阶不确定混沌系统同步控制方法，可以使驱动–响应系统快速同步；张燕兰 [6] 针对一类分数阶Rayleigh-Duffling-like系统，通过改进控制器和未知参数的辨识规则，实现了广义同步；仲启龙等 [7] 采用主动滑模控制方法，研究了分数阶系统的混沌同步问题；SY Shao等 [8] 分析了分数阶Chua系统的错位同步和应用问题，提升了分数阶Chua系统的理论深度；刘文等 [9] 在文献 [8] 的研究基础上，得到了混沌系统的错位跟踪同步的方法。从以上研究结论可以看出，虽然人们在混沌同步领域取得很多有价值的理论成果，但却很少利用自适应滑模控制方法分析错位同步问题。为此，本文针对分数阶四翼混沌系统，分析证明了驱动系统和响应系统同步的充分条件，进一步讨论了自适应滑模错位同步控制问题。试验结果表明：通过选择适当的控制律和滑模面，分数阶四翼系统的驱动–响应系统完全可以实现混沌同步。

2. 分数阶四翼系统

数学上关于分数阶导数的定义有很多种，本文采用Caputo分数阶导数的定义方式 [10]：称

$_{a} D_{t}^{α} = D_{t}^{- (n - α)} \frac{d^{n}}{d t^{n}} x (t) = \frac{1}{Γ (n - α)} \int_{t_{0}}^{t} {(t - τ)}^{n - α - 1} x^{(n)} (τ) d τ, n - 1 < α < n \in Z^{+}, t > a$

为 $α$ 阶Caputo微分算子， $Γ$ 为Gamma函数。

由于多翼吸引子混沌系统在很多领域都显现出了应用价值，所以它的构建方法、分析过程和实现形式成为了广大学者研究关注的内容。由于构造四翼混沌系统的方法有很多种形式，出现了形形色色的各种整数阶、分数阶四翼混沌系统，比如通过系统耦合的方式构造四翼混沌系统；在混沌系统中加入一个控制器，通过调整参数来构造四翼混沌系统；也可以通过加载常数控制器构造四翼混沌系统。Y Guo等 [11] 研究了分数阶齐四翼混沌系统中的拓扑结构；Donato C等 [12] 研究了耦合经典的lorenz系统产生的四翼混沌系统；J Ma [13] 等通过对三维自治混沌系统添加控制器，提出了一种新的超混沌四翼系统，并利用拓扑理论和计算机辅助证明加以验证，通过电子电路设计得以实现。

我们考虑如下一类分数阶四翼混沌系统 [14] [15] $D_{t}^{q} x = f (x)$ ：

$\begin{array}{l} D_{t}^{q} x_{1} = a x_{1} + k x_{2} - x_{2} x_{3} \\ D_{t}^{q} x_{2} = - b x_{2} - x_{3} + x_{1} x_{3} \\ D_{t}^{q} x_{3} = - x_{1} - c x_{3} + x_{1} x_{2} \end{array}$ (1)

当 $b = 12, c = 5, k = 1, q = 0.9, a \in [3.6, 8.8] \cup [9, 9.2]$ 时系统呈现混沌态，如图1所示。H Jia等 [14] 分析了该分数阶系统混沌的特性，并研究了电路实现；HY Jia等 [15] 利用频域和时域方法对该混沌系统做了更深层次的分析。

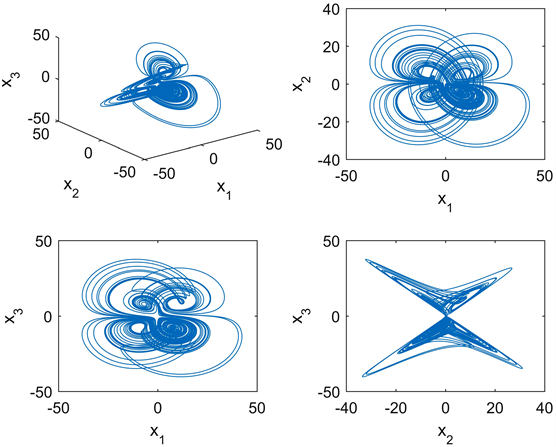
Figure 1. Chaotic attractor of system (1)

图1. 系统(1)的吸引子

3. 错位同步

假设系统(1)为驱动系统，它对应的响应系统 $D_{t}^{q} y = f (y) + d (y) + u$ 可以设计为：

$\begin{array}{l} D_{t}^{q} y_{1} = a y_{1} + k y_{2} - y_{2} y_{3} + d_{1} (t) + u_{1} \\ D_{t}^{q} y_{2} = - b y_{2} - y_{3} + y_{1} y_{3} + d_{2} (t) + u_{2} \\ D_{t}^{q} y_{3} = - y_{1} - c y_{3} + y_{1} y_{2} + d_{3} (t) + u_{3} \end{array}$ (2)

式中 $u_{i}$ 表示控制器， $d_{i} (t)$ 表示外部扰动，有界。

系统(1)和(2)均为三维系统，定义系统错位同步误差变量如下：

$e (t) = y (t) - Δ x ( t )$

式中， $Δ$ 表示错位矩阵， $Δ \in R^{3 \times 3}$ 表示每行每列有且仅有一个元素为1、其他元素均为0的三阶非奇异矩阵，满足条件的 $Δ$ 共有 $3!$ 个不同的矩阵，其中有 $3! - 1$ 个 $Δ$ 不是对角阵。在 $Δ$ 不是对角阵时，有

$\lim_{t \to \infty} e (t) = \lim_{t \to \infty} (y (t) - Δ x (t)) = 0$ ，称两系统是错位同步。

不妨以如下错位矩阵为例

$Δ = (\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix})$

即错位误差变量 $e_{1} = y_{1} - x_{2}$ ， $e_{2} = y_{2} - x_{3}$ ， $e_{3} = y_{3} - x_{1}$ ，由系统(1)和(2)得到误差系统如下：

$\begin{array}{l} D_{t}^{q} e_{1} = a y_{1} + k y_{2} - y_{2} y_{3} + b x_{2} + x_{3} - x_{1} x_{3} + d_{1} (t) + u_{1} \\ D_{t}^{q} e_{2} = - b y_{2} - y_{3} + y_{1} y_{3} + x_{1} + c x_{3} - x_{1} x_{2} + d_{2} (t) + u_{2} \\ D_{t}^{q} e_{3} = - y_{1} - c y_{3} + y_{1} y_{2} - a x_{1} - k x_{2} + x_{2} x_{3} + d_{3} (t) + u_{3} \end{array}$ (3)

同步误差变量同样可以定义为 $e (t) = Δ y (t) - x (t)$ ，有相同的结果。

假设1：设外部扰动 $d_{i} (t)$ 有界，即存在 $m_{i}, n_{i} > 0$ 使得： $| d_{i} (t) | < m_{i}$ 。

假设2： $m_{i} (i = 1, 2, 3)$ 为未知的常数。

假设3： $| d_{2} (t) | \leq ε | e_{1} (t) |, | d_{3} (t) | \leq ε | e_{2} (t) |, | d_{1} (t) | \leq ε | e_{3} (t) |, 0 < ε < 1$ 。

假设4： $e_{i} (t) = 0$ 时， $f_{i} (t) = 0$ ， $e_{i} (t) \neq 0$ 时， $f_{i} (t) \neq 0$ 。

引理1 [16]：如果存在实对称正定矩阵P，使得 $J (x (t)) = x^{T} (t) P D_{t}^{α} x (t) < 0$ , $(0 < α \leq 1)$ ，则分数阶自治非线性微分方程

$D_{t}^{α} x (t) = f (x ( t ) )$

的分数阶系统渐近稳定。

引理2： [17] (Barbalat引理)若函数 $f (t)$ 在 $[0, + \infty)$ 上一致连续，并且广义积分 $\int_{0}^{+ \infty} f (t) d t$ 存在，则有 $\lim_{t \to \infty} f (t) = 0$ 。

定理1：假设1~4都成立，取滑模面

$s (t) = D_{t}^{q - 1} (e_{1} + e_{2} + e_{3})$ ，

取控制器：

$\begin{array}{l} u_{1} = - (a + 1) y_{1} - k y_{2} + y_{2} y_{3} - (b - 1) x_{2} - x_{3} + x_{1} x_{3} - {\hat{m}}_{1} sgn (s) \\ u_{2} = (b - 1) y_{2} + y_{3} - y_{1} y_{3} - x_{1} - (c - 1) x_{3} + x_{1} x_{2} - {\hat{m}}_{2} sgn (s) \\ u_{3} = 2 y_{1} + y_{2} - x_{3} + c y_{3} - y_{1} y_{2} + a x_{1} + (k - 1) x_{2} - x_{2} x_{3} - {\hat{m}}_{3} sgn (s) - η sgn (s) \end{array}$ (4)

式中， $η > 0$ 表示趋近速度的增益系数， ${\hat{m}}_{i}$ 为 $m_{i}$ 的估计值，若定义自适应律： ${\dot{\hat{m}}}_{i} = | s |, {\hat{m}}_{i} (0) = {\hat{m}}_{i 0}, i = 1, 2, 3$ ，则分数阶四翼系统的驱动–响应系统(1)与(2)是滑模自适应同步的。

证明：当状态轨迹位于滑模面上时，

$s (t) = 0$ ， $\dot{s} (t) = 0$ ，

由于

$s (t) = D_{t}^{q - 1} (e_{1} + e_{2} + e_{3}) = 0$ ，

则，

$D_{t}^{1 - q} D_{t}^{q - 1} (e_{1} + e_{2} + e_{3}) = 0$ ，

从而，

$e_{1} + e_{2} + e_{3} = 0$ 。 (5)

利用控制器(4)的表达式可得，

$D_{t}^{q} e_{1} = - e_{1} + d_{2} (t) - {\hat{m}}_{1} sgn (s)$ ， $D_{t}^{q} e_{2} = - e_{2} + d_{3} (t) - {\hat{m}}_{2} sgn (s)$ ，

在滑模面上 $s = 0$ 时

$D_{t}^{q} e_{1} = - e_{1} + d_{2} (t)$ ， $D_{t}^{q} e_{2} = - e_{2} + d_{3} (t)$ ，

另一方面

$D_{t}^{q} e_{3} = e_{1} + e_{2} + d_{1} (t) - {\hat{m}}_{3} sgn (s) - η sgn (s)$ 。

由于在滑模面上 $s = 0$ ，根据(5)得到

$e_{1} + e_{2} = - e_{3} \Rightarrow D_{t}^{q} e_{3} = - e_{3} + d_{1} (t)$ ，

由引理1，则当 $e_{i} (t) \neq 0$ 时

$J = e^{T} D_{t}^{q} e = {[\begin{matrix} e_{1} & e_{2} & e_{3} \end{matrix}]}^{T} [\begin{matrix} D_{t}^{q} e_{1} \\ D_{t}^{q} e_{2} \\ D_{t}^{q} e_{3} \end{matrix}] = {[\begin{matrix} e_{1} & e_{2} & e_{3} \end{matrix}]}^{T} [\begin{matrix} - e_{1} + d_{2} (t) \\ - e_{2} + d_{3} (t) \\ - e_{3} + d_{1} (t) \end{matrix}] \leq - (1 - ε) \sum_{i = 1}^{3} {| e_{i} |}^{2} < 0$ ，

根据引理1，误差系统的解

$e_{i} (t) \to 0$ , $i = 1, 2, 3$ 。

所以在滑模面上 $s = 0$ ，误差系统(3)是渐进稳定的。

当状态轨迹不位于滑模面上时，选取Lyapunov函数，

$V (t) = \frac{1}{2} s^{2} (t) + \frac{1}{2} \sum_{i = 1}^{3} {({\hat{m}}_{i} - m_{i})}^{2}$

求导得：

$\begin{matrix} \dot{V} = s \dot{s} + \sum_{i = 1}^{3} ({\hat{m}}_{i} - m_{i}) | s | \\ = s [- e_{1} + d_{1} - {\hat{m}}_{1} sgn s - e_{2} + d_{2} - {\hat{m}}_{2} sgn s + e_{1} + e_{2} + d_{3} \\ - {\hat{m}}_{3} sgn s - η sgn s] + \sum_{i = 1}^{3} ({\hat{m}}_{i} - m_{i}) | s | \\ \leq \sum_{i = 1}^{3} m_{i} | s | - \sum_{i = 1}^{3} {\hat{m}}_{i} | s | \\ = - η | s (t) | < 0 \end{matrix}$ 。

通过积分计算得：

$\int_{0}^{t} | s (τ) | d τ \leq \frac{\int_{0}^{t} \dot{V} (τ) d τ}{- η} \leq \frac{V (0) - V (\infty)}{- η} \leq V (0) < \infty$ 。

所以 $s (t)$ 是有界的，并且是可积的。根据由引理2，当 $s (t) \to 0$ 时

$e_{i} (t) \to 0$ ， $i = 1, 2, 3$ 。

综合以上证明过程，误差系统(3)趋近于零。

由定理1知道，当状态轨迹在滑膜面上时，误差系统趋于稳定；当状态轨迹不在滑膜面上时，在控制器作用下，系统逐渐趋于滑膜面，从而误差系统趋于稳定，根据相关定义，驱动–响应系统实现错位同步。

4. 比例积分同步

假设(1)为驱动系统，则对应的响应系统为

$\begin{array}{l} D_{t}^{q} y_{1} = a y_{1} + k y_{2} - y_{2} y_{3} + u \\ D_{t}^{q} y_{2} = - b y_{2} - y_{3} + y_{1} y_{3} \\ D_{t}^{q} y_{3} = - y_{1} - c y_{3} + y_{1} y_{2} \end{array}$ (6)

假设误差变量

$e_{1} = y_{1} - x_{1}$ ， $e_{2} = y_{2} - x_{2}$ ， $e_{3} = y_{3} - x_{3}$ ，

根据式(1)、式(6)可得误差系统如下：

$\begin{array}{l} D_{t}^{q} e_{1} = a e_{1} + k e_{2} - y_{2} y_{3} + x_{2} x_{3} + u \\ D_{t}^{q} e_{2} = - b e_{2} - e_{3} + y_{1} y_{3} - x_{1} x_{3} \\ D_{t}^{q} e_{3} = - e_{1} - c e_{3} + y_{1} y_{2} - x_{1} x_{2} \end{array}$ ， (7)

定理2: 假设常数 $λ > 0$ ， $| k e_{1} - y_{2} y_{3} + x_{2} x_{3} | < λ | e_{1} |, | x_{1} e_{2} | < λ | e_{1} |$ ，设计滑模面

$s (t) = D_{t}^{q - 1} e_{1} + \int_{0}^{t} [λ e_{1} (τ) - k e_{2} (τ) + y_{2} (τ) y_{3} (τ) - x_{2} (τ) x_{3} (τ)] d τ$ ，

取控制器：

$u = - (λ + a) e_{1} - η sgn s$

其中 $η > 0$ ，则分数阶四翼系统的驱动–响应系统(1)与(6)是同步的。

证明：在滑模面上， $s (t) = 0$ ， $\dot{s} (t) = 0$ ，由于

$\dot{s} = D_{t}^{q} e_{1} + λ e_{1} - k e_{2} + y_{2} y_{3} - x_{2} x_{3} = (a + λ) e_{1} + u = 0$ ，

定义等效控制器 $u_{e q} = - (λ + a) e_{1}$ ，定义切换控制器 $u_{s w} = - η sgn s$ ，

设计控制器

$u = u_{e q} + u_{s w} = - (λ + a) e_{1} - η sgn s$ 。

构造 $V (t) = \frac{1}{2} e_{1}^{2}$ ，根据引理1可得

$D_{t}^{q} V (t) \leq e_{1} D_{t}^{q} e_{1} = e_{1} [k e_{2} - y_{2} y_{3} + x_{2} x_{3} - λ e_{1}] < 0$ ，

所以 $e_{1} \to 0$ ；由于 $y_{1} y_{2} - x_{1} x_{2} = e_{1} y_{2} + x_{1} e_{2}$ ，根据式(7)的第三式，

$D_{t}^{q} e_{3} = - e_{1} - c e_{3} + e_{1} y_{2} + x_{1} e_{2}$ ，

根据混沌系统的有界性及 $e_{1} \to 0$ ，得 $D_{t}^{q} e_{3} = - c e_{3}$ ，所以 $e_{3} \to 0$ 。利用式(7)的第二式

$D_{t}^{q} e_{2} = - b e_{2} - e_{3} + y_{1} y_{3} - x_{1} x_{3} = - b e_{2} - e_{3} + e_{1} y_{3} - x_{1} e_{3}$ ，

因为 $e_{1} \to 0$ , $e_{3} \to 0$ ，所以 $D_{t}^{q} e_{2} = - b e_{2}$ , $e_{2} \to 0$ 。

不在滑膜面上时，构造 $V (t) = \frac{1}{2} s^{2}$ ，求导得

$\dot{V} (t) = s \dot{s} = s [- η sgn s] = - η | s | < 0$ ，

由引理2得 $s \to 0$ 。

5. 数值仿真试验

为了验证上述方法的正确性，以Matlab2018b为试验平台，利用常规的预估校正算法，对分数阶四翼系统做数值仿真。系统参数 $a = 5, b = 12, c = 5, k = 1, q = 0.9$ ， $({\hat{m}}_{1}, {\hat{m}}_{2}, {\hat{m}}_{3}) = (0.8, 0.6, 0.5)$ 此时系统为混沌态；选取外部扰动项为 $d_{1} (t) = 0.2 \cos (t)$ ， $d_{2} (t) = 0.6 \sin (t)$ ， $d_{3} (t) = \cos (3 t)$ ；理论上讲，按照我们的同步方案，对任意初始值，系统均可实现错位同步，取系统状态变量初始值为 $(x_{1} (0), x_{2} (0), x_{3} (0)) = (1, 1, 1)$ ， $(y_{1} (0), y_{2} (0), y_{3} (0)) = (- 1, - 1, - 1)$ 。

图2为分数阶系统在定理1同步方案下，两系统错位同步的误差系统曲线图形；图3为分数阶系统在定理2同步方案下，两系统同步的误差系统曲线图形，其中参数 $η = 0.8$ , $λ = 1$ ；从图2和图3可以看出，两种同步方案均使系统状态逐渐趋近一致，我们所设计的方案下，系统在很短时间内即可实现错位同步与同步，所设计方案是可行的和有效的。

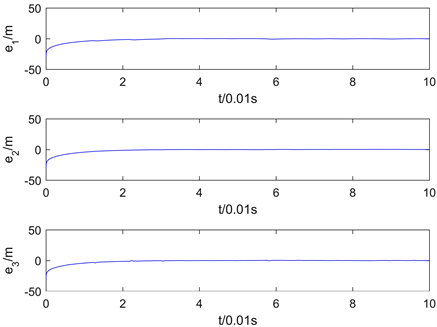
Figure 2. Error curve of system dislocation synchronization in Theorem 1

图2. 定理1的系统错位同步误差曲线

Figure 3. Synchronization error curve of two systems in theorem 2

图3. 定理2的两系统同步误差曲线

在我们做数值仿真过程中，在不满足定理条件下的控制器同样也有可能实现同步，是因为我们给出的同步条件是充分条件，而非充分必要条件。

6. 结论

本文通过构造一个分数阶滑膜面和控制器、设计合适的自适应律，研究了一类分数阶四翼混沌系统的滑模错位同步控制问题，通过假设条件和严格的证明得到了驱动–响应系统取得滑模同步的充分条件；并进一步利用比例积分滑模的方法实现同步。数值仿真试验表明，该方法是有效的，获得结论是正确的。

基金项目

本文受到国家社会科学基金项目：基于蝴蝶效应的非线性金融复杂系统模型及稳定性分析(NO. 18BJL073)和河南省高等学校骨干教师培养计划项目：基于混沌理论的非线性金融系统模型及相关问题研究(2017GGJS193)的共同资助。

文章引用

时文俊,丁艳风,蔡国梁. 分数阶四翼混沌系统滑模同步
Sliding Mode Synchronization of a Four-Wing Fractional-Order Chaotic Systems[J]. 应用数学进展, 2020, 09(10): 1693-1700. https://doi.org/10.12677/AAM.2020.910196

参考文献

1. 孙宁, 张化光, 王智良. 不确定分数阶混沌系统的滑模投影同步[J]. 浙江大学学报(工学版), 2010, 44(7): 1288-1291.

2. 胡满峰, 徐振源. Lorenz混沌系统的非线性反馈错位同步控制[J]. 系统工程与电子技术, 2007, 29(8): 1346-1348.

3. Sun, J., Wang, Y., Yao, L., et al. (2015) General Hybrid Projective Complete Dislocated Synchronization between a Class of Chaotic Real Nonlinear Systems and a Class of Chaotic Complex Nonlinear Systems. Applied Mathematical Modelling, 39, 6150-6164. ://doi.org/10.1016/j.apm.2015.01.049

4. Xu, Y., Zhou, W. and Fang, J.A. (2009) Hybrid Dislocated Control and General Hybrid Projective Dislocated Synchronization for the Modified Lü Chaotic System. Chaos, Solitons and Fractals, 42, 1305-1315. ://doi.org/10.1016/j.chaos.2009.03.023

5. 余明哲, 张友安. 一类不确定分数阶混沌系统的滑模自适应同步[J]. 北京航空航天大学学报, 2014, 40(9): 1276-1280.

6. 张燕兰. 分数阶Rayleigh-Duffling-Like系统的自适应追踪广义投影同步[J]. 动力学与控制学报, 2014, 12(4): 348-352.

7. 仲启龙, 邵永辉, 郑永爱. 分数阶混沌系统的主动滑模同步[J]. 动力学与控制学报, 2015, 13(1): 18-22.

8. Shao, S.Y., Min, F.H., Ma, M.L., et al. (2013) Non-Inductive Modular Circuit of Dislocated Synchronization of Fractional-Order Chua’s System and Its Application. Acta Physica Sinica, 62, 1-27.

9. 刘文, 常艳娜, 赵静一, 等. 一个三维混沌系统的错位跟踪同步[J]. 内蒙古农业大学学报, 2017, 38(1): 70-74

10. Podlubny (1999) Fractional Differential Equation. Academic Press, New York.

11. Guo, Y. and Qi, G. (2015) Topological Horseshoe in a Fractional-Order Qi Four-Wing Chaotic System. Journal of Applied & Computation, 5, 168-176.

12. Donato, C. and Giuseppe, G. (2009) Fractional-Order Chaos: A Novelfour-Wing Attractor in Coupled Lorenz Systems. International Journal of Bifurcation & Chaos, 19, 3329-3338. ://doi.org/10.1142/S0218127409024785

13. Ma, J., Chen, Z.Q., Wang, Z.L. and Zhang, Q. (2015) A Four-Wing Hyper-Chaotic Attractor Generated from a 4-D Memristive System with a Line Equilibrium. Nonlinear Dynamics, 81, 1275-1288. ://doi.org/10.1007/s11071-015-2067-4

14. Jia, H., Chen, Z. and Qi, G. (2014) Chaotic Characteristics Analysis and Circuit Implementation for a Fractional-Order System. IEEE Transactions on Circuits and Systems I: Regular Papers, 61, 845-853. ://doi.org/10.1109/TCSI.2013.2283999

15. Jia, H.Y., Guo, Z.Q., Qi, G.Y., et al. (2018) Analysis of a Four-Wing Fractional-Order Chaotic System via Frequency-Domain and Time-Domain Approaches and Circuit Implementation for Secure Communication. Optik, 155, 233-241. ://doi.org/10.1016/j.ijleo.2017.10.076

16. 胡建兵, 赵灵冬. 分数阶系统稳定性理论与控制研究[J]. 物理学报, 2013, 62(24): 5041-5047.

17. 梅生伟, 申铁龙, 刘志康. 现代鲁棒控制理论与应用[M]. 北京: 清华大学出版社, 2003.

期刊菜单