Advances in Applied Mathematics
Vol.
10
No.
02
(
2021
), Article ID:
40396
,
6
pages
10.12677/AAM.2021.102045
两类双圈图最大特征值的比较
秦旭艳,李玉瑛,郝艺方
太原理工大学数学学院,山西 晋中

收稿日期:2021年1月7日;录用日期:2021年2月11日;发布日期:2021年2月18日

摘要
本文研究了两类连通双圈图的最大特征值,得出了随着n的增大,双圈图 和 的最大特征值也随之增大;同时给出了在 的条件下, 和 的最大特征值的比较。
关键词
双圈图,特征值

Comparison of the Maximum Eigenvalues of Two Types of Bicyclic Graphs
Xuyan Qin, Yuying Li, Yifang Hao
School of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi
Received: Jan. 7th, 2021; accepted: Feb. 11th, 2021; published: Feb. 18th, 2021

ABSTRACT
This paper studies the maximum eigenvalues of two types of connected bicyclic graphs, and finds that as n increases, the maximum eigenvalues of bicyclic graphs and also increase; at the same time, it also gives a comparison of the maximum eigenvalues of and under the condition of .
Keywords:Bicyclic Graph, Eigenvalue

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 背景介绍
设
是一个简单的无向连通图,其中顶点集
,边集
如果
,那么G被称为双圈图,图G的顶点数n被称为G的阶。G的邻接矩阵记为
,如果
与
相邻,那么 ,否则
,否则 。
。 的特征多项式记为
的特征多项式记为 ,
, 的最大特征值也被称为G的谱半径,用
的最大特征值也被称为G的谱半径,用 表示。由于
表示。由于 是非负不可约对称矩阵,所以它的最大特征值为单根,且所有的特征值均为实数,记其特征值为
是非负不可约对称矩阵,所以它的最大特征值为单根,且所有的特征值均为实数,记其特征值为 ,由矩阵理论知
,由矩阵理论知 有正特征向量与
有正特征向量与 对应,我们称与
对应,我们称与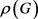 对应的正单位特征向量为G的Perron向量。
对应的正单位特征向量为G的Perron向量。
在图论中,G的一条路是指一个有限非空序列 ,它的项交替地为顶点和边,且
,它的项交替地为顶点和边,且 互不相同,使得对
互不相同,使得对 ,
, 的端点是
的端点是 和
和 ,那么称W是从
,那么称W是从 到
到 的一条长为k的路。特殊地,在G中,若
的一条长为k的路。特殊地,在G中,若 和
和 重合,则W是一个长为k的圈,记为
重合,则W是一个长为k的圈,记为 。在具有n个顶点的图G中,其中一个点的度为
。在具有n个顶点的图G中,其中一个点的度为 ,分别与其他
,分别与其他 个点相连,其他
个点相连,其他 个点只与度为
个点只与度为 的点相连,这样的图称为星图
的点相连,这样的图称为星图 。
。
我们将圈 的某一点与圈
的某一点与圈 的某一点粘合,仅在粘合点处连接星图
的某一点粘合,仅在粘合点处连接星图 得到的n阶连通双圈图记作
得到的n阶连通双圈图记作 (粘合点为星图的非一度点) (见图1)。将圈
(粘合点为星图的非一度点) (见图1)。将圈 上的任意两点相连,形成圈
上的任意两点相连,形成圈 和圈
和圈 ,在其中任意一个连接处连接星图
,在其中任意一个连接处连接星图 得到的n阶连通双圈图记作
得到的n阶连通双圈图记作 (见图1)。
(见图1)。

Figure 1.Bicyclic Graphs  and
and 
图1.双圈图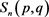 和
和
关于双圈图的研究已经有很长时间了,双圈图的性质也逐步被人们发现。1986年,Brualdi和Solheid [1] 提出,给定一个图的集合,在这个集合中找出谱半径的上界,并刻画达到这个上界的极图。2004年,Yu和Tian [2] 找出了在具有匹配数m的n个顶点的所有双圈图中谱半径最大的一类图。2010年,Liu Yingluan和Liu Bolian [3] 找出了双圈图度序列π相同的情况下谱半径最大的一类图。但是没有对几类比较有特点的双圈图的最大特征值展开详细研究。
1.2. 本文贡献
基于以上研究,本文主要通过对两类连通双圈图 和
和 的最大特征值进行研究,利用二次型以及双圈图的邻接矩阵的特征多项式进行分析,确定它们的最大特征值的大小。
的最大特征值进行研究,利用二次型以及双圈图的邻接矩阵的特征多项式进行分析,确定它们的最大特征值的大小。
2. 预备知识
如果 ,
, ,并且
,并且 是
是 在
在 上的限制,则称图H是G的子图。如果
上的限制,则称图H是G的子图。如果 ,但
,但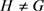 时,则记为
时,则记为 ,并且H称为G的真子图。
,并且H称为G的真子图。
定理2.1 [4]:设G是具有n个顶点的连通图,如果 是G的一个子图,那么
是G的一个子图,那么 。
。
定理2.2 [4]:对于任意正整数p和q, 的特征值为
的特征值为 ,
, 和0,并且特征值0的重数为
和0,并且特征值0的重数为 。特殊地,
。特殊地, 的特征值为
的特征值为 ,
, 和0,并且特征值0的重数为
和0,并且特征值0的重数为 。
。
定理2.3 [4]:设G是一个有 个顶点的连通图,并令A是G的邻接矩阵,那么下面命题成立:
个顶点的连通图,并令A是G的邻接矩阵,那么下面命题成立:
1) A有一个特征值 ,存在一个对应的特征向量
,存在一个对应的特征向量 。
。
2) 对于A的任意一个特征值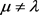 ,有
,有 。此外,当且仅当G是二部图时,
。此外,当且仅当G是二部图时, 才是A的一个特征值。
才是A的一个特征值。
3) 如果 是A的对应于特征值
是A的对应于特征值 的一个特征向量,那么存在一个
的一个特征向量,那么存在一个 ,使得
,使得 。
。
在定理2.4的1)中提到的G的这种特征值 ,被称为G的Perron特征值,而其对应的特征向量x被称为Perron特征向量。注意到2)中G的Perron特征值和最大特征值(即
,被称为G的Perron特征值,而其对应的特征向量x被称为Perron特征向量。注意到2)中G的Perron特征值和最大特征值(即 )相同。如3)中所示,Perron特征向量是唯一的,最多相差一个标量倍。
)相同。如3)中所示,Perron特征向量是唯一的,最多相差一个标量倍。
定理2.4 [4]:设A是一个 对称矩阵,且其特征值
对称矩阵,且其特征值 以非增顺序排列。令
以非增顺序排列。令 表示常用的欧几里得范数,即
表示常用的欧几里得范数,即 。那么
。那么 。
。
定理2.5 [5]:令G是具有 (
( )个顶点的图,顶点集
)个顶点的图,顶点集 。如果
。如果 是通过在G中的
是通过在G中的 上添加k个悬挂点
上添加k个悬挂点 得到,那么
得到,那么

其中 对应于顶点
对应于顶点 ,且
,且 。
。
3. 主要结论
定理3.1:当双圈图 的点数n变大时,其最大特征值也变大,即
的点数n变大时,其最大特征值也变大,即 (见图2)。
(见图2)。

Figure 2.Bicyclic Graphs  and
and 
图2.双圈图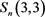 和
和
证明:设 是
是 的单位Perron向量,
的单位Perron向量, 是对应于
是对应于 的顶点
的顶点 的分量值。记
的分量值。记 是
是 的邻接矩阵,
的邻接矩阵, 是
是 的邻接矩阵,即
的邻接矩阵,即 ,其中,
,其中, 。现在
。现在 的图上增加一个孤立点
的图上增加一个孤立点 ,所得到的图记作
,所得到的图记作 ,其对应的邻接矩阵为
,其对应的邻接矩阵为 。
。 的最大特征值
的最大特征值 对应的特征向量为
对应的特征向量为 。
。
又因为 ,
, ,所以
,所以 。
。
若 ,则
,则 成立,即
成立,即

成立。
然而

矛盾。
因此,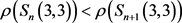 。
。
定理3.2:当双圈图 的点数n变大时,其最大特征值也变大,即
的点数n变大时,其最大特征值也变大,即 (见图3)。
(见图3)。

Figure 3.Bicyclic Graphs  and
and 
图3.双圈图 和
和
证明:同定理3.1的证明,很容易证得 。
。
定理3.3:当 时,
时, (见图4)。
(见图4)。
证明: 删除
删除 个
个 的悬挂点得到的图记为G,
的悬挂点得到的图记为G, 删除
删除 个
个 的悬挂点得到的图记为
的悬挂点得到的图记为 。
。
由定理2.5可得:

Figure 4. Bicyclic Graphs  and
and 
图4. 双圈图 和
和


其中 ;
; ;
;
那么 ,
, 分别是
分别是 和
和 的最大根。又因为
的最大根。又因为 和
和 都以
都以 作为真子图,所以根据定理2.1和定理2.2可得:
作为真子图,所以根据定理2.1和定理2.2可得:

令 ,则
,则 ,
, 。
。
所以,当 且
且 时,有
时,有 ,进一步有,
,进一步有, ,那么
,那么 ,而
,而 ,则
,则 。
。
又因为 ,并且当
,并且当 时,
时, ,所以根据
,所以根据 的性质,当
的性质,当 时,有
时,有 。
。
例3.1:通过Matlab很容易计算出 ,
, ,
, ,
,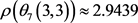 ,
, ,
, ,从而
,从而 ,
, ,
, ,
, ,
, 。因此,在一定程度上验证了定理3.1~定理3.3的正确性。
。因此,在一定程度上验证了定理3.1~定理3.3的正确性。
4. 结论与展望
本文主要研究了两类连通双圈图 和
和 的最大特征值,利用二次型以及双圈图的邻接矩阵的特征多项式进行分析确定它们最大特征值的大小,从而得出一些有意义的结论,使我们对这两类双圈图的最大特征值有了更加深入的理解。
的最大特征值,利用二次型以及双圈图的邻接矩阵的特征多项式进行分析确定它们最大特征值的大小,从而得出一些有意义的结论,使我们对这两类双圈图的最大特征值有了更加深入的理解。
我们也将会进一步研究双圈图 和
和 随n的变化其最小特征值的变化情况,以及在n一定的条件下,双圈图
随n的变化其最小特征值的变化情况,以及在n一定的条件下,双圈图 和
和 的最小特征值的比较。
的最小特征值的比较。
文章引用
秦旭艳,李玉瑛,郝艺方. 两类双圈图最大特征值的比较
Comparison of the Maximum Eigenvalues of Two Types of Bicyclic Graphs[J]. 应用数学进展, 2021, 10(02): 396-401. https://doi.org/10.12677/AAM.2021.102045
参考文献
- 1. Brualdi, R.A. and Solheid, E.S. (1986) On the Spectral Radius of Complementary Acyclic Matrices of Zeros and Ones. SIAM Journal on Algebraic and Discrete Methods, 7, 265-272. https://doi.org/10.1137/0607030
- 2. Yu, A.M. and Tian, F. (2004) On the Spectral Radius of Bicyclic Graphs. MATCH Communications in Mathematical and in Computer Chemistry, 88, 91-101.
- 3. Liu, Y.L. and Liu, B.L. (2010) The Spectral Radius of Bicyclic Graphs with Prescribed Degree Sequences. Linear Algebraic and Its Applications, 433, 1015-1023. https://doi.org/10.1016/j.laa.2010.04.036
- 4. Bapat, R.B. (2010) Graphs and Matrices. Springer, London. https://doi.org/10.1007/978-1-84882-981-7
- 5. 刘木伙, 柳柏濂. 利用计算机计算n阶图的特征多项式的方法[J]. 高等学校计算数学学报, 2012, 34(3): 260-266.