Advances in Applied Mathematics
Vol.
10
No.
03
(
2021
), Article ID:
40956
,
6
pages
10.12677/AAM.2021.103073
基于Cahn-Hilliard方程的二值图像修复方法
霍俊蓉,张荣培,刘昊
沈阳师范大学,数学与系统科学学院,辽宁 沈阳

收稿日期:2021年2月8日;录用日期:2021年3月8日;发布日期:2021年3月16日

摘要
图像修复作为图像处理的一个分支,在计算机视觉、天文学、生物学等领域中有广泛的应用。本文使用修正Cahn-Hilliard方程进行二值图像修复,采用二阶有限差分方法将含有非线性项的方程在空间上进行离散,采用Crank-Nicolson方法将其在时间上进行离散,应用快速离散余弦变换结合不动点迭代法求解全离散格式下的方程组。基于该模型的图像修复数值方法具有参数少、存储量小、计算效率高等优点。最后,给出数值实验,数值结果验证该数值方法能有效地进行图像修复与去噪。
关键词
图像修复,Cahn-Hilliard方程,二值图像,有限差分法
Binary Image Inpainting Method Based on Cahn-Hilliard Equation
Junrong Huo, Rongpei Zhang, Hao Liu
School of Mathematics and Systematic Sciences, Shenyang Normal University, Shenyang Liaoning
Received: Feb. 8th, 2021; accepted: Mar. 8th, 2021; published: Mar. 16th, 2021

ABSTRACT
As a branch of image processing, image inpainting is widely used in computer vision, astronomy, biology and other fields. In this paper, the modified Cahn-Hilliard equation is used for binary image inpainting. The second-order finite difference method is used to discretize the equation with nonlinear term in space, and the Crank-Nicolson method is used to discretize it in time. The fast discrete cosine transform combined with fixed point iteration method is used to solve the equations in the fully discrete scheme. The numerical method of image inpainting based on this model has the advantages of few parameters, small storage and high computational efficiency. Finally, numerical experiments are given to verify the effectiveness of the proposed method.
Keywords:Image Inpainting, Cahn-Hilliard Equation, Binary Image, Finite Difference Method

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
图像处理的一个重要任务是根据从图像受损区域周围收集到的信息来填充图像的缺失部分,称为图像修复。图像在传输和保存等过程中,可能会有部分信息丢失或者被污染,图像修复一般包括缺损信息的填补和去除噪声,通过未受破坏区域的像素信息,还原被破坏像素以及丢失像素。图像修复是图像退化过程的逆过程,可以恢复由于划伤、老化或自然因素等原因而发生部分破损的图像,也可以恢复被其他对象遮挡的图像。因此,被广泛用于修复古老字画 [1],视频后期处理 [2],减少医学成像伪影 [3] 以及卫星图像处理 [4] 等众多领域中。Bertalmio等人 [5] 首次提出数字图像修复的概念,并将偏微分方程的思想引入图像修复中。
近年来,许多学者对图像修复及其数值模型进行了研究。包括TV修复模型 [6] [7],MS修复模型 [8],快速图像修复算法 [9],自适应图像修复算法 [10] 以及应用于二值图像修复的修正Cahn-Hilliard [11] 模型,由于Cahn-Hilliard模型的非凸性,一般采用凸分裂 [12] 的思想进行求解,但是需要定义多个参数。本文应用有限差分方法空间求解Cahn-Hilliard方程,利用Kronecker积写出二维拉普拉斯算子的微分矩阵并将其特征分解,结合快速离散余弦变换实现了快速求解。与原有的方法比较,本文所采用的方法选取的参数更少、存储量小、可以提高计算效率。
2. 数值方法
在二值图像情况下,修正的Cahn-Hilliard方程可更加快速高效地进行图像修复 [13]。本文考虑Cahn-Hilliard方程的修正方程(1):
(1)
其中 为可操作区域; 为自由能函数; 为拉普拉斯算子; 为Lyapunov泛函;当 时 ,当 时 ; 为给定区域 内的待处理图像, 为信息缺失区域, 为有效信息区域; 为待定参数。图像修复,即为根据待修复图像在有效信息区域中 的数值,对信息缺失区域中的像素值进行计算与匹配,进而得到完整图像的过程。设初始值为 并且边界条件为齐次Neumann边界:
(2)
本文考虑用直线 在区域 上打网格,其中网格节点为 ,网格步长为 ,。定义离散解 为 阶的矩阵 ,表示网格节点 处的数值解。由齐次Neumann边界条件,以及网格内部点 和边界处的二阶导数差分格式,得到该方程在 方向的微分矩阵分别为 和 。其中矩阵 为 阶的矩阵, ,,,,矩阵 中其他位置的元素均为0。同理有 为 阶的矩阵。
将解矩阵 按列向量化后得到 ,记为 。设 分别为 阶单位矩阵,利用微分矩阵 和 以及Kronecker积的定义,可将(1)式的中心差分格式写成如下形式:
(3)
其中
下面将矩阵 特征分解得到
(4)
其中 为对角矩阵,其对角元素 为矩阵 的特征值,矩阵 中 , ,同理,对 有类似的结果。接下来,对矩阵 做特征分解。由 以及Kronecker积的性质 [13] 可以得到
(5)
其中 为 阶的对角矩阵,且对角元素均为正数。
本文应用Grank-Nicolson的差分方法对(3)式进行时间离散得到
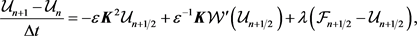 (6)
(6)
其中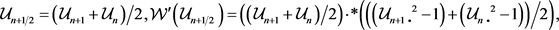 ,。上式中运算符“
”表示对向量中每个元素进行平方运算;运算符“
”表示对两个向量中对应元素进行乘法运算。应用快速离散余弦变换结合不动点迭代法求解(6)式,迭代初值选取为
。
,。上式中运算符“
”表示对向量中每个元素进行平方运算;运算符“
”表示对两个向量中对应元素进行乘法运算。应用快速离散余弦变换结合不动点迭代法求解(6)式,迭代初值选取为
。
3. 数值实验
首先,对截断的条形图进行修复处理,如图1所示。其中,图1(b)中灰色区域表示修复区域,即信息缺失区域。采用修正的Cahn-Hilliard方程对截断的条形图分别进行修复10、20、35、55次,可以看出截断的条形图逐渐修复,到迭代55次时图像已经基本修补完成。

Figure 1. Repair of truncated bar image
图1. 截断条形图像的修复
接下来,对带有涂鸦的图像进行修复处理,如图2所示。其中,图2(b)为带有涂鸦的熊猫图片,表示待修复图像,该图以涂鸦部分为修复区域。采用修正的Cahn-Hilliard方程对图片的缺失部分进行修复5、10、15、20次,可以看出涂鸦区域随着迭代次数的增加,变得越来越细小,直至消失。图2(f)为迭代20次后的修复图像,可以看出图像中破损的部分已经得到有效修补,该图像显示的即为修复后完整的熊猫图片。

Figure 2. Restoration of graffiti in images
图2. 图像中涂鸦的修复
最后,对带有水印的图像进行修复处理,如图3所示。其中,图3(b)为带有水印的向日葵图片,表示待修复图像,该图以水印部分为修复区域。采用修正的Cahn-Hilliard方程对图像分别进行修复5、10、20、30次,可以看出迭代30次时图像中的水印已消失,图像修复完成。

Figure 3. Watermark restoration in image
图3. 图像中水印的修复
4. 结论
本文利用四阶修正Cahn-Hilliard方程对截断的条形图以及带噪声的图像进行修复,在空间和时间上分别应用有限差分方法和Crank-Nicolson方法对修正的Cahn-Hilliard方程进行离散并进行快速求解。数值实验结果表明,该模型对于截断的条纹或有涂鸦、水印的二值图像均有良好的修复效果。本文提出的数值方法可以高效地对图像进行修复与去噪,使图像中受污染区域的像素信息得到合理填充,更加适合人眼视觉。同时,该方程可用的快速数值技术在处理较大的数据集上也更加有效,一定程度上有助于加快计算速度,提高图像处理效率。
基金项目
辽宁省自然科学基金(20180550996)资助的课题。
文章引用
霍俊蓉,张荣培,刘 昊. 基于Cahn-Hilliard方程的二值图像修复方法
Binary Image Inpainting Method Based on Cahn-Hilliard Equation[J]. 应用数学进展, 2021, 10(03): 674-679. https://doi.org/10.12677/AAM.2021.103073
参考文献
- 1. 陈永, 艾亚鹏, 郭红光. 改进曲率驱动模型的敦煌壁画修复算法[J]. 计算机辅助设计与图形学学报, 2020, 32(5): 787-796.
- 2. 谷伊, 韩军. 基于样本的图像修补方法在视频修复中的应用[J]. 应用科学学报, 2010, 28(2): 163-169.
- 3. Gu, J., Zhang, L., Yu, G., et al. (2006) X-Ray CT Metal Artifacts Reduction through Curvature Based Sinogram Inpainting. Journal of X-Ray Science and Technology, 14, 73-82.
- 4. Chen, X., Yang, S., Wang, X., et al. (2010) Satellite Image Blind Restoration Based on Surface Fitting and Iterative Multishrinkage Method in Redundant Wavelet Domain. Optik, 121, 1909-1911. https://doi.org/10.1016/j.ijleo.2009.05.015
- 5. Bertalmio, M., Sapiro, G., Caselles, V., et al. (2000) Image Inpainting. SIGGRAPH Conference, New Orleans, LA, July 2000, 417-424. https://doi.org/10.1145/344779.344972
- 6. 杨陈东, 侯海娜. 基于改进TV修复模型的椒盐噪声去除算法[J]. 计算机与数字工程, 2016, 44(11): 2118-2123.
- 7. Shen, J. and Chan, T.F. (2002) Mathematical Models for Local Nontexture Inpaintings. SIAM Journal on Applied Mathematics, 62, 1019-1043. https://doi.org/10.1137/S0036139900368844
- 8. Haehnle, J. and Prohl, A. (2011) Mumford-Shah-Euler Flow with Sphere Constraint and Applications to Color Image Inpainting. SIAM Journal on Imaging Sciences, 4, 1200-1233. https://doi.org/10.1137/100795620
- 9. 赵颜伟, 李象霖. 基于CDD模型的快速图像修复算法[J]. 计算机仿真, 2008(10): 223-227.
- 10. 印勇, 李丁, 胡琳昀. 采用CDD模型的自适应图像修复算法[J]. 重庆大学学报, 2013, 36(4): 80-86.
- 11. Bertozzi, A., Esedoglu, S. and Gillette, A. (2007) Analysis of a Two-Scale Cahn-Hilliard Model for Binary Image Inpainting. Multiscale Modeling & Simulation, 6, 913-936. https://doi.org/10.1137/060660631
- 12. Greer, J.B., Bertozzi, A.L. and Sapiro, G. (2006) Fourth Order Partial Differential Equations on General Geometries. Journal of Computational Physics, 216, 216-246. https://doi.org/10.1016/j.jcp.2005.11.031
- 13. Strang, G. (2007) Computational Science and Engineering. Vol. 791, Wellesley-Cambridge Press, Wellesley, 284-285.