上海理工大学理学院，上海

收稿日期：2024年2月1日；录用日期：2024年2月20日；发布日期：2024年4月17日

摘要

马尔可夫过程最初由俄罗斯数学家马尔可夫(Markov)于1906年研究而得名，它是一类典型的具有马氏性的随机过程。马氏性是指现在发生的事情与过去曾发生的事件无关。简言之，在已知“现在”的条件下，“将来”与“过去”是独立的。马尔可夫过程理论已发展得较为成熟，在自然科学、工程技术及经济金融管理等领域都有广泛的应用。本文以马尔可夫模型的基本理论为出发点，将马尔可夫模型运用在经济金融领域，使用马尔可夫预测模型和加权马尔可夫预测模型对股票价格的波动情况进行预测分析，并以浦发银行的股票价格数据为例进行实证分析。

关键词

马尔可夫链，平稳分布，马尔可夫预测模型，加权马尔可夫预测模型

Markov Prediction Models and Its Applications in the Analysis on the Volatility of Stock Prices

Chunpeng Zhang, Jiying Ma^*

College of Science, University of Shanghai for Science and Technology, Shanghai

Received: Feb. 1^st, 2024; accepted: Feb. 20^th, 2024; published: Apr. 17^th, 2024

ABSTRACT

Markov process was originally named after the research of Russian mathematician Markov in 1906. It is a typical stochastic process with Markov property. Markov property refers to the fact that what is happening now is unrelated to past events. In short, given the known “present”, the “future” and “past” are independent. The theory of Markov process has been developed maturely, and it has been widely used in natural science, engineering technology, economic and financial management and other fields. This article takes the basic theory of Markov models as the starting point, applies Markov models to the field of economics and finance, uses Markov prediction models and weighted Markov prediction models to predict and analyze the volatility of stock prices, and conducts experiments using the stock price data of Shanghai Pudong Development Bank as an example.

Keywords:Markov Chain, Stationary Distribution, Markov Prediction Model, Weighted Markov Prediction Model

Copyright © 2024 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

马尔可夫链是人类历史上第一个从理论上提出且进行研究的随机过程模型。1906年，俄罗斯数学家马尔可夫(Markov)发表了一篇题为《大数定理关于相依变量的扩展》的论文，该文第一次提到了这个环环相扣的随机序列 [1] 。此随机变量序列有非常优良的性质，即当一部分随机变量的值已经知道后，下一个随机变量的分布情况仅与之前一个随机变量有关，与前面的一系列随机变量都无关，这种性质后来被称为马氏性。通俗地讲，马氏性是指现在发生的事情与过去曾发生的事件无关。

而随着马尔可夫过程理论的不断发展，其研究的不再单单只是离散时间，而是发展到了连续时间和任意相位时间。柯尔莫哥洛夫(Kolmogorov)将众多理论思想结合在一起，抽象出了一般情况下的马尔可夫过程，之后，他和辛钦(Khinchin)一起研究了平稳过程的一些理论。1951年，伊藤清在前人的基础上，创立了布朗运动的随机微分方程方面的理论，开创了马尔可夫过程研究的新道路。之后，随机过程理论不断被发展和完善，直到1960年前后，法国的布尔巴基学派发展了随机过程的一般理论 [1] 。

马尔可夫过程理论在自然科学、工程技术及经济金融管理等领域都有广泛的应用。我国的市场经济发展迅速，人们的生活水平有了明显的提高，可支配收入也水涨船高，人们的金融意识和投资意识也伴随着收入的增加而增强，因此投资理财渐渐成为一个热门话题，到2022年，我国资本市场个人投资者已经突破了1.97亿。个人投资者往往欠缺金融知识，风险意识淡薄，风险的承受能力较差，因此需要一种经济预测法，对股票价格的波动趋势和波动区间进行分析和预测。投资者可以根据对股票价格的预测作为参考依据，来判断股票市场的发展趋势，以确定相应的投资方式。

股价预测一直是一项具有挑战性的任务。在大多数情况下，一般的投资者仅能通过股票的历史表现，凭经验做出投资决策，但这样会有一定的风险。良好的经济预测法可以一定程度上降低由于不确定性带来的风险，比如马尔可夫预测法就可以大大削弱这些不确定性带来的影响 [2] 。当某一经济指标在一段区间内具有“马氏性”时，即可建立马尔可夫模型对这段区间里的指标变化进行预测分析。通常情况下，股票价格一般与过去的价格无关，只与近期的价格相关，因此股票价格可以通过马尔可夫预测法进行预测分析 [3] 。

将马尔可夫链应用在金融领域在国内外已经有许多结果 [4] 。例如，文献 [5] 利用马尔可夫模型对我国股市走向进行了预测分析，其研究结果发现，马尔可夫链所具有的无后效性非常适合股市指数的预测分析。文献 [6] 整合了正则马尔可夫链和吸收型马尔可夫链来获取更多的时间信息，从而进行股票价格的预测。而文献 [7] 将马尔可夫模型运用到构建投资组合当中。本文主要介绍马尔可夫链相关的基本概念和理论，应用马尔可夫预测模型和加权马尔可夫预测模型对股票价格的波动情况进行预测分析，并以浦发银行的股票价格数据为例进行实证分析。

2. 马尔可夫链及马尔可夫预测法

2.1 马尔可夫链的基本概念

定义2.1 对于随机过程 $\left\{X_n,n=0,1,2,\cdots \right\}$ ，若它只包含有限个或可列个值，且对于 $\forall n\ge 0$ ，任意的状态 $i,j,i_0,i_1,\cdots ,i_{n-1}$ 有

$P\left\{X_{n+1}=j|X_n=i,X_{n-1}=i_{n-1},\cdots ,X_1=i_1,X_0=i_0\right\}=P\left\{X_{n+1}=j|X_n=i\right\}$ (2.1)

则把该随机过程称为马尔可夫链。

在(2.1)式中， $X_n=i$ 表示该随机过程在n时刻时处于状态i， $S=\left\{0,1,2,\cdots \right\}$ 称为该过程的状态空间。(2.1)式描述的是对于一个随机过程，其将来时刻的状态 $X_{n+1}$ 仅取决于当前时刻的状态 $X_n$ ，而与过去时刻的状态 $X_0,X_1,\cdots ,X_{n-1}$ 无关的特性，我们将这种特性称为马尔可夫性 [8] 。

定义2.2 $P_{ij}\left(n\right)=P\left\{X_{n+1}=j|X_n=i\right\}$ 称为马尔可夫链 $\left\{X_n,n=0,1,2,\cdots \right\}$ 的由时刻n的状态i转移至时刻 $n+1$ 的状态j的一步转移概率，简称转移概率。

定义2.3 若马尔可夫链的转移概率 $P_{ij}\left(n\right)=P\left\{X_{n+1}=j|X_n=i\right\}=p_{ij}$ 与n无关，仅与状态 $i,j$ 有关，则称这个马尔可夫链是时齐的；否则，称为非时齐的。

本文中，仅讨论时齐的马尔可夫链，并简称为马尔可夫链。

此时， $p_{ij}$ 可以排成一个矩阵的形式，即

$P=\left[\begin{array}{ccccc}{p}_{00}& p_{01}& \cdots & p_{0j}& \cdots \\ p_{10}& p_{11}& \cdots & p_{1j}& \cdots \\ ⋮& ⋮& \ddots & \cdots & ⋮\\ p_{i0}& p_{i1}& \cdots & p_{ij}& \cdots \\ ⋮& ⋮& \cdots & ⋮& \cdots \end{array}\right]$ (2.2)

我们称 $P$ 为一步转移概率矩阵，一般简称为转移矩阵，其中 $p_{ij}\left(i,j\in S\right)$ 满足下列性质：

1) 非负性： $0\le p_{ij}\le 1,i,j\in S$ ；

2) 正则性： ${\displaystyle {\sum }_{j\in S}{p}_{ij}}=1,\forall i\in S$ 。

定义2.4 考虑条件概率

$p_{ij}^{\left(n\right)}=P\left\{X_{n+m}=j|X_m=i\right\},i,j\in S;m\ge 0;n\ge 1,$ (2.3)

该概率表示状态i经过n步转移至状态 的转移概率，称之为马尔可夫链的n步转移概率，同时，称 $P^{\left(n\right)}=\left(p_{ij}^{\left(n\right)}\right)$ 为n步转移概率矩阵。

定义2.5 对于马尔可夫链，若

$p_j=\underset{i\in S}{{\displaystyle \sum }}{p}_i{p}_{ij}$

则称概率分布 $\left\{p_j,j\in S\right\}$ 为平稳分布。

定义2.6 若所有状态都两两互通，正常返，且周期都是1，就称马尔可夫链是遍历的。若马尔可夫链是遍历的，则极限

${\lim }_{n\to \infty }{p}_{ij}^{\left(n\right)}={\pi }_j,j\in S,$ (2.4)

称为马尔可夫链的极限分布。

定理2.1 Chapman-Kolmogorov方程(C-K方程) $\forall m,n\ge 0,i,j\in S$ 有

1) $p_{ij}^{(m+n)}={\displaystyle \underset{k\in S}{\sum }{p}_{ik}^{(m)}{p}_{kj}^{(n)}}$ , (2.5)

2) $P^{\left(n\right)}=P\cdot P^{\left(n-1\right)}=P\cdot P\cdot P^{\left(n-2\right)}=\cdots =P^n$ . (2.6)

定理2.2 若马尔可夫链是不可约的，非周期的，则

1) 若它是遍历的，则马尔可夫链的极限分布 ${\pi }_j={\lim }_{n\to \infty }{p}_{ij}^{\left(n\right)}>0\left(j\in S\right)$ 就是平稳分布，且平稳分布是唯一的；

2) 若状态都是瞬过的或零常返的，则不存在平稳分布。

上述两个定理的证明可以参考有关随机过程的教材 [8] [9] 。

2.2. 马尔可夫预测法

首先我们要对指标进行聚类，最常见的聚类方法是根据样本均值和样本方差来刻画的。现在假设指标值依次为 $x_1,x_2,\cdots ,x_n$ ，样本均值为 $\bar{x}$ ，样本方差为 $s=\sqrt{\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2}}$ 。根据中心极限定理可知， $P\left\{\bar{x}-2s\le Y\le \bar{x}+2s\right\}=2\Phi \left(2\right)-1=0.9544$ ； $P\left\{\bar{x}-s\le Y\le \bar{x}+s\right\}=2\Phi \left(1\right)-1=0.68$ 。所以可以把指标划分为 $\left(-\infty ,\bar{x}-2s\right)$ ， $\left(\bar{x}-2s,\bar{x}-s\right)$ ， $\left(\bar{x}-s,\bar{x}+s\right)$ ， $\left(\bar{x}+s,\bar{x}+2s\right)$ ， $\left(\bar{x}+2s,+\infty \right)$ 这五个状态。

但是在实际应用中，这种分法指标会过于集中在中间三类中，因此，一般将指标值的变化区间分为 $\left(-\infty ,\bar{x}-a_{1}s\right)$ ， $\left(\bar{x}-a_{1}s,\bar{x}-a_{2}s\right)$ ， $\left(\bar{x}-a_{2}s,\bar{x}+a_{2}s\right)$ ， $\left(\bar{x}+a_{2}s,\bar{x}+a_{1}s\right)$ ， $\left(\bar{x}+a_{1}s,+\infty \right)$ ， $$ ， $a_2\in \left[0.3,0.6\right]$ 。

假设 $x_1,x_2,\cdots ,x_n$ 是一个具有“马氏性”的时间序列，该时间序列包含m个状态，即该序列的状态空间为 $S=\left\{1,2,\cdots ,m\right\}$ ，用 $h_{ij}$ 表示序列中从状态i经过一次转移到状态j的频数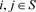，。(注：在这里只讨论一步转移概率)将 $h_{ij}$ 组成的矩阵 ${\left(h_{ij}\right)}_{i,j\in S}$ 叫做“转移频数矩阵” [10] 。

然后将频数转矩转化为概率矩阵。在统计中，把一个状态的频数除以各个状态的频数之和作为该状态的频率，因此我们考虑，将频数矩阵的第 $\left(i,j\right)$ 个元素 $h_{ij}$ 除以第i行之和，得到的值记作 $p_{ij}$ 。即 $p_{ij}=\frac{h_{ij}}{{{\displaystyle \sum }}_{j=1}^m{h}_{ij}}$ ， $p_{ij}$ 的实际意义是从状态i到状态j的一步转移频率，但根据统计中的知识可以知道，当n充分大后，频率可以近似等于概率。所以，我们可以认为 $p_{ij}$ 是一步转移概率，进而我们可得转移概率矩阵 $P={\left(p_{ij}\right)}_{i,j\in S}$ 。

首先我们要验证时间序列的马氏性。计算出转移频率矩阵的第j列的列和，再将其除以矩阵中各个数据之和，将得到的值记作 $p_{•j}$ ，称为“边际概率”，即 $p_{•j}=\frac{{{\displaystyle \sum }}_{i=1}^m{h}_{ij}}{{{\displaystyle \sum }}_{i=1}^m{{\displaystyle \sum }}_{j=1}^m{h}_{ij}}$ 。

当n充分大之后，可以认为统计量

${\chi }^2=2{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{h}_{ij}\left|\log \frac{p_{ij}}{p_{•j}}\right|}}$

服从 ${\chi }^2$ 分布，而其分布的自由度是 ${\left(m-1\right)}^2$ ，其中 $p_{ij}$ 是转移概率。

给定显著性水平a，查表即可得分位数 ${\chi }_a^2\left({\left(m-1\right)}^2\right)$ ，通过计算得到 ${\chi }^2$ 的值，将其两者相比较，当 ${\chi }^2>{\chi }_a^2\left({\left(m-1\right)}^2\right)$ 时，我们就可以认为序列 $\left\{x_i\right\}$ 在很大程度上是具有马氏性的；反之，则不可以将该时间序列来当作马尔可夫链进行处理。

确定时间序列的马氏性之后，我们就可以使用马尔可夫预测法进行预测了，其具体操作步骤如下：

1) 通过均值—方差聚类法对股票价格时间序列进行聚类分析，然后确定分级标准，即求出马尔可夫链的状态空间 $S=\left\{1,2,\cdots ,n\right\}$ 。然后根据之前确定的分级标准，将序列中的各个指标进行分级处理；

2) 建立转移频率矩阵和转移概率矩阵，然后对得到结果进行统计分析计算，处理过后就可以得到马尔可夫链的一步转移概率矩阵 $P=\left(p_{ij}\right),i,j\in S$ 。然后对数据进行马氏性检验，若通过检验，则可继续进行操作；若失败，则表示该组股票价格序列不具有马氏性，不可以通过该方法预测分析；

3) 任意选定一个时刻作为初始时刻，若该时期对应的指标值属于状态i，则可认为初始分布为：

$P\left(0\right)=\left(0,\cdots ,0,1,0,\cdots ,0\right)$ .

$P\left(0\right)$ 是一个单位行向量，其中 $P\left(0\right)$ 的第i个分量为1，其余分量都是0。则可认为下一时期的绝对分布为：

$P\left(1\right)=P\left(0\right)P=\left(p_1\left(1\right),p_1\left(2\right),\cdots ,p_1\left(n\right)\right)$ ,

则该时期的预测状态j满足 $p_1\left(j\right)=\max \left\{p_1\left(i\right),i\in S\right\}$ 。

若要预测往后k个时期的状态值，则可由

$P\left(k\right)=P\left(0\right)P^k=\left(p_k\left(1\right),p_k\left(2\right),\cdots ,p_k\left(n\right)\right)$ ,

则该时期的预测状态 满足 $p_k\left(j\right)=\max \left\{p_k\left(i\right),i\in S\right\}$ ；

4) 之后可以对马尔可夫链的遍历性和平稳分布再进行讨论。

2.3. 加权马尔可夫预测法

股票的价格序列是一组相关的随机变量，所以自相关系数描述了各个时段的股票价格之间的相关关系的强弱。因此，我们可以确定前面几个时段的股票价格对应的状态之后，使用前面时段的状态来进行该段时间的状态预测，然后根据前面几个时段与该时段之间的相关关系的强弱，即自相关系数的大小来进行加权预测和分析。

这种预测分析可以充分地利用历史数据，而且经过这样的分析之后确定的投资策略也应该是更加合理的，这就符合加权马尔可夫预测法的基本模型。加权马尔可夫预测的基本操作步骤如下 [10] ：

1) 对股票价格的时间序列使用均值—方差聚类生成，进而确定股票价格的分级标准，并按照标准确定各个时段股票价格所处的状态；

2) 马氏性检验；

3) 计算各阶自相关系数 $r_k$ ， $k\in S$ ，

$r_k=\frac{{\displaystyle \underset{l=1}{\overset{n-k}{\sum }}\left(x_l-\bar{x}\right)\left(x_{l+k}-\bar{x}\right)}}{{\displaystyle \underset{l=1}{\overset{n}{\sum }}{\left(x_l-\bar{x}\right)}^2}},$

其中 $r_k$ 为第k阶的自相关系数； $x_l$ 为第l时段的股票价格； $\bar{x}$ 为股票价格的均值；n表示股票价格序列的数量；

4) 对各阶的自相关系数进行规范化处理，即：

$w_k=\frac{\left|r_k\right|}{{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left|r_k\right|}},$

其中m为该预测所需要的最大阶数，而 $w_k$ 可以作为各阶马尔可夫链的权重；

5) 对(4)得到的结果进行统计分析处理，即可得到不同步长马尔可夫链的转移概率矩阵，这代表了预测价格状态转移的概率；

6) 分别以之前几个时段的股票价格所对应的状态作为初始状态，然后使用不同步长的转移概率矩阵即可推算出该时段股票价格的状态概率 $p_i^{\left(k\right)},i\in S$ ，k为步长，且 $1\le k\le m$ ；

7) 得到同一状态的各个预测概率之后，可以通过加权求和计算出股票价格处于该状态的概率。即 $p_i={\displaystyle {\sum }_{k=1}^m{w}_k{p}_i^{\left(k\right)}},i\in S$ ，而 ${\max }_{i\in S}\left\{p_i\right\}$ 就可以当作该时刻股票价格的预测状态。而之后该时段股票价格确

定之后，可以根据分级标准确定股票价格所处的状态，然后将该状态加入原价格序列，再重复上述(1)~(7)的操作，便可以继续去预测下一个时段股票价格的状态。

3. 浦发银行的实例分析

3.1. 马尔可夫预测法分析股票价格

本文以浦发银行(SH.600000)为例，此次研究的是从2019年7月1日到2019年8月13日的32个时间序列，进行收盘价的价格预测(表1)。以下数据来自于证券数据平台(http://www.baostock.com/)。

表1. 2019年7月1日至2019年8月13日股票价格指数表

即股票价格时间序列为 $x_1=11.71,x_2=11.61,\cdots ,x_{32}=11.33$ ，可求得 $\bar{x}=\frac{1}{32}{\displaystyle \underset{i=1}{\overset{32}{\sum }}{x}_i}\approx 11.52$ ， $s=\sqrt{\frac{1}{31}{\displaystyle \underset{i=1}{\overset{32}{\sum }}{\left(x_i-\bar{x}\right)}^2}}\approx 0.21$ ，取定 ${\alpha }_1=1.5,{\alpha }_2=0.5$ ，状态空间 $S=\left\{1,2,3,4,5\right\}$ ，对应指标的状态为 $y_1=4,y_2=3,\cdots ,y_{32}=2$ (表2)。

表2. 状态–价格区间表

表3. 价格状态转移情况表

由表3可得对应的转移频数矩阵 $H={\left(h_{ij}\right)}_{5\times 5}$ 和转移概率矩阵 $P={\left(p_{ij}\right)}_{5\times 5}$ ：

$H={\left(h_{ij}\right)}_{5\times 5}=\left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 1& 4& 2& 0& 0\\ 0& 3& 11& 0& 1\\ 0& 0& 2& 0& 0\\ 0& 0& 0& 1& 4\end{array}\right]$ ,

$P={\left(p_{ij}\right)}_{5\times 5}=\left[\begin{array}{ccccc}\frac{1}{2}& \frac{1}{2}& 0& 0& 0\\ \frac{1}{7}& \frac{4}{7}& \frac{2}{7}& 0& 0\\ 0& \frac{1}{5}& \frac{11}{15}& 0& \frac{1}{15}\\ 0& 0& 1& 0& 0\\ 0& 0& 0& \frac{1}{5}& \frac{4}{5}\end{array}\right]=\left[\begin{array}{ccccc}0.5& 0.5& 0& 0& 0\\ 0.14& 0.57& 0.29& 0& 0\\ 0& 0.2& 0.73& 0& 0.07\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 0.2& 0.8\end{array}\right]$ .

根据转移概率矩阵P可得边际转移概率值： $p_{·1}=\frac{9}{14}\approx 0.64,p_{·2}=\frac{89}{70}\approx 1.27,p_{·3}=\frac{212}{105}\approx 2.02,p_{·4}=\frac{1}{5}=0.2,p_{·5}=\frac{13}{15}\approx 0.87$ ，故可计算出统计量χ²的大小，即得表4。

表4. 统计量 ${\chi }^2=2{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{h}_{ij}\left|\log \frac{p_{ij}}{p_{•j}}\right|}}$ 计算表

给定显著性水平 $\alpha =0.05$ ，根据 ${\chi }^2$ 分位数表可得 ${\chi }_{\alpha }^2\left({\left(m-1\right)}^2\right)={\chi }_{0.05}^2\left(16\right)=26.296$ ，因为 $\chi =61.56>{\chi }_{0.05}^2\left(16\right)=26.296$ ，所以可以认为浦发银行的股票价格的时间序列满足马氏性。

再根据C-K方程，可求得各阶的转移概率矩阵 $P^{\left(2\right)}$ 、 $P^{\left(3\right)}$ 、 $P^{\left(4\right)}$ 、 $P^{\left(5\right)}$ ：

$P^{\left(2\right)}=P^2=\left[\begin{array}{ccccc}0.32& 0.54& 0.14& 0& 0\\ 0.15& 0.45& 0.45& 0& 0.02\\ 0.03& 0.26& 0.59& 0.01& 0.11\\ 0& 0.20& 0.73& 0& 0.07\\ 0& 0& 0.20& 0.16& 0.64\end{array}\right]$ ,

$P^{\left(3\right)}=P^3=\left[\begin{array}{ccccc}0.24& 0.49& 0.26& 0& 0.01\\ 0.14& 0.41& 0.41& 0& 0.04\\ 0.05& 0.28& 0.52& 0.02& 0.13\\ 0.03& 0.26& 0.59& 0.01& 0.11\\ 0& 0.04& 0.31& 0.13& 0.52\end{array}\right]$ ,

,

$P^{\left(5\right)}=P^5=\left[\begin{array}{ccccc}0.16& 0.42& 0.37& 0.01& 0.04\\ 0.12& 0.37& 0.42& 0.01& 0.08\\ 0.07& 0.29& 0.46& 0.03& 0.15\\ 0.06& 0.29& 0.48& 0.3& 0.14\\ 0.02& 0.12& 0.40& 0.08& 0.38\end{array}\right]$ .

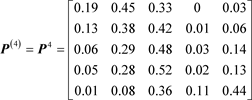以2019年8月13日作为初始日期，因为该日的收盘价为11.33，处于状态2，所以初始向量 $P^{\left(0\right)}=\left(01000\right)$ 。假定预测五个工作日的股票价格，则可根据i步概率转移向量为 $P^{\left(i\right)}=\left(01000\right)P^i$ ， $i=1,2,3,4,5$ ，得到表5。

表5. 预测状态与实际对照图

同时，考虑所建立的马尔可夫链的平稳分布，根据定理2.2的证明过程可知，构造下述线性方程组 ${\pi }_j={\displaystyle \underset{i\in S}{\overset{}{\sum }}{\pi }_i{p}_{ij}^{(n)}}$ ，即可得到平稳分布 $\left\{{\pi }_j,j\in S\right\}$ ：

$\{\begin{array}{l}{\pi }_1=0.5{\pi }_1+0.14{\pi }_2\hfill \\ {\pi }_2=0.5{\pi }_1+0.57{\pi }_2+0.2{\pi }_3\hfill \\ {\pi }_3=0.29{\pi }_2+0.73{\pi }_3+{\pi }_4\hfill \\ {\pi }_4=0.2{\pi }_5\hfill \\ {\pi }_5=0.07{\pi }_3+0.8{\pi }_5\hfill \\ {\pi }_1+{\pi }_2+{\pi }_3+{\pi }_4+{\pi }_5=1\hfill \end{array}$

可得平稳分布为 $\pi =\left(0.0840.30000.4340.0300.152\right)$ 。

预测分析：使用马尔可夫预测法由表5可以看出：1) 8月14日，有57%的概率股票价格会落在区间[11.205, 11.415)中，而8月14日的实际股票价格也确实在该区间中；2) 8月15日，股票价格以45%的概率落在区间[11.205, 11.415)中，虽然预测结果是正确的，但是预测分析显示，落在区间[11.415, 11.625)也有38%的概率；3) 在8月16日，预测股票价格会以相同的41%的概率落在区间[11.205, 11.415)和区间[11.415, 11.625)中，虽然实际股票价格落在区间[11.205, 11.415)中，但是，这样的预测带有很大的不可控性，无法使股票价格以更大的概率落在正确的区间，一旦时间过长，预测的准确度就不够了。但是预测结果还是具有一定的参考价值，短期内如果突然出现状态1的价格，则可以考虑买入该股票，因为从平稳分布可以看出来，该股票短期内会有74%的概率落在状态2和状态3中，则买入者仍可以赚取一部分差价。

3.2. 加权马尔可夫预测法分析股票价格

在上面数据的基础上，我们使用加权马尔可夫预测法进行预测分析。

计算各阶的自相关系数 $r_k,k=1,2,3,4,5$ ，然后将各阶自相关系数规范化求得w_k，即可得到表6。

再计算各个步长的转移概率矩阵，即可得：

表6. 各阶 $r_k$ 及马尔可夫链权重表

$P={\left(p_{ij}\right)}_{5\times 5}=\left[\begin{array}{ccccc}\frac{1}{2}& \frac{1}{2}& 0& 0& 0\\ \frac{1}{7}& \frac{4}{7}& \frac{2}{7}& 0& 0\\ 0& \frac{1}{5}& \frac{11}{15}& 0& \frac{1}{15}\\ 0& 0& 1& 0& 0\\ 0& 0& 0& \frac{1}{5}& \frac{4}{5}\end{array}\right]=\left[\begin{array}{ccccc}0.5& 0.5& 0& 0& 0\\ 0.14& 0.57& 0.29& 0& 0\\ 0& 0.2& 0.73& 0& 0.07\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 0.2& 0.8\end{array}\right]$ ,

$P^{\left(2\right)}={\left(p_{ij}^{\left(2\right)}\right)}_{5\times 5}=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ \frac{1}{7}& \frac{3}{7}& \frac{3}{7}& 0& 0\\ \frac{1}{14}& \frac{1}{7}& \frac{9}{14}& 0& \frac{1}{7}\\ 0& \frac{1}{2}& \frac{1}{2}& 0& 0\\ 0& 0& \frac{1}{5}& \frac{1}{5}& \frac{3}{5}\end{array}\right]=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0.14& 0.43& 0.43& 0& 0\\ 0.07& 0.14& 0.65& 0& 0.14\\ 0& 0.5& 0.5& 0& 0\\ 0& 0& 0.2& 0.2& 0.6\end{array}\right]$ ,

$P^{\left(3\right)}={\left(p_{ij}^{\left(3\right)}\right)}_{5\times 5}=\left[\begin{array}{ccccc}0& \frac{1}{2}& \frac{1}{2}& 0& 0\\ 0& \frac{1}{2}& \frac{1}{2}& 0& 0\\ \frac{1}{14}& \frac{3}{14}& \frac{1}{2}& 0& \frac{3}{14}\\ \frac{1}{2}& 0& \frac{1}{2}& 0& 0\\ 0& \frac{1}{5}& \frac{1}{5}& \frac{1}{5}& \frac{2}{5}\end{array}\right]=\left[\begin{array}{ccccc}0& 0.5& 0.5& 0& 0\\ 0& 0.5& 0.5& 0& 0\\ 0.07& 0.215& 0.5& 0& 0.215\\ 0.5& 0& 0.5& 0& 0\\ 0& 0.2& 0.2& 0.2& 0.4\end{array}\right]$ ,

$P^{\left(4\right)}={\left(p_{ij}^{\left(4\right)}\right)}_{5\times 5}=\left[\begin{array}{ccccc}0& \frac{1}{2}& \frac{1}{2}& 0& 0\\ 0& \frac{1}{5}& \frac{4}{5}& 0& 0\\ 0& \frac{5}{14}& \frac{5}{14}& 0& \frac{2}{7}\\ \frac{1}{2}& 0& \frac{1}{2}& 0& 0\\ \frac{1}{5}& \frac{1}{5}& \frac{1}{5}& \frac{1}{5}& \frac{1}{5}\end{array}\right]=\left[\begin{array}{ccccc}0& 0.5& 0.5& 0& 0\\ 0& 0.2& 0.8& 0& 0\\ 0& 0.36& 0.36& 0& 0.28\\ 0.5& 0& 0.5& 0& 0\\ 0.2& 0.2& 0.2& 0.2& 0.2\end{array}\right]$ ,

$P^{\left(5\right)}={\left(p_{ij}^{\left(5\right)}\right)}_{5\times 5}=\left[\begin{array}{c}\begin{array}{ccc}0& 1& \begin{array}{ccc}0& 0& 0\end{array}\end{array}\\ \begin{array}{ccc}0& 0& \begin{array}{ccc}1& 0& 0\end{array}\end{array}\\ \begin{array}{ccc}0& \frac{2}{7}& \begin{array}{ccc}\frac{5}{14}& 0& \frac{5}{14}\end{array}\end{array}\\ \begin{array}{ccc}0& 1& \begin{array}{ccc}0& 0& 0\end{array}\end{array}\\ \begin{array}{ccc}\frac{2}{5}& \frac{1}{5}& \begin{array}{ccc}\frac{1}{5}& \frac{1}{5}& 0\end{array}\end{array}\end{array}\right]=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0.28& 0.36& 0& 0.36\\ 0& 1& 0& 0& 0\\ 0.4& 0.2& 0.2& 0.2& 0\end{array}\right]$ .

最后根据2019.08.07至2019.08.13五个交易日的收盘价和相应的转移概率矩阵对8月14日的收盘价进行预测，得表7。

表7. 8月14日收盘价预测表

${\max }_{i\in S}\left\{p_i\right\}=0.41$ ，此时状态为S₂，故预测8月14日的状态为2。而8月14日的实际状态为2，因此预测合理。

预测分析：预测结果表明，在8月14日，股票价格以41%的概率落在区间[11.205, 11.415)内，以33%的概率落在区间[11.415, 11.625)内，以25%的概率落在区间(−∞, 11.205)内。由此可以看出，该预测法仍保留着传统预测方法的准确度，能够在一定程度上，很好地预测出所需要的结果。与此同时，该方法仍保留了可以通过多状态的概率来对持有股票进行保留观望的优点。加权马尔可夫预测模型在很大程度保留了优点的同时，弥补了一些由于时效性而带来的缺点，以及优化了由于金融的特殊性而带来的问题。

4. 总结

马尔可夫链是随机过程中一个十分典型的代表，其本身具有的马尔可夫性能很好地契合许多生活中事物特性，如本文所应用的股票价格序列。而马尔可夫链具有许多优良的性质，如平稳分布，遍历性，可约性等，我们可以通过马尔可夫链普遍具有的性质，去寻找构建的马尔可夫链的独特性质。本文首先应用传统的马尔可夫预测模型对股票价格进行预测分析，但是由于金融市场的波动性较大，该预测法预测的结果具有很强的时效性。接着我们使用加权马尔可夫预测法，该方法可以充分利用历史数据，并且能够在一定程度上降低特殊事件对某一特定时刻所带来的影响。

通过对浦发银行股票价格的试验数据表明，在使用马尔可夫预测法时，短期内会有一个超过40%概率的区间，这个区间的概率明显大于其他区间的概率。但是，随着时间的增加，分布会逐渐趋向于平稳分布，再使用这样的预测结果明显是不合理的。为此我们引入加权马尔可夫预测模型，通过新数据的加入来更新权重比例，既能保留马尔可夫预测法本身的准确度，又可以根据日期更新带来的变化，延长预测的日期。虽然无法做到长期的预测，但在一定程度上可以弥补传统马尔可夫预测法时效过短的问题。

虽然该预测法只有短期的预测准确度，但与已有文献相比，文献 [2] [3] 中只给出了股票价格的走势情况，即与前一日相比是增长还是下降，并没有给出具体的涨幅或者下降的范围。本文通过引入聚类分析法，将股票价格进行聚类后，可以大致预测出股票价格落在的区间范围。这样有一个显著的好处，即使某一日股票价格呈现的可能是下降趋势，但是与购入时的价格相比还是有明显的涨幅，此时可以不急于抛售股票，再观望一段时间，给使用者更多的选择空间。

文章引用

张春鹏,马纪英. 马尔可夫预测模型对股票价格波动的预测分析
Markov Prediction Models and Its Applications in the Analysis on the Volatility of Stock Prices[J]. 运筹与模糊学, 2024, 14(02): 433-444. https://doi.org/10.12677/orf.2024.142148

参考文献