Statistics and Application
Vol.
08
No.
05
(
2019
), Article ID:
32709
,
6
pages
10.12677/SA.2019.85086
Hierarchical Linear Regression Analysis of Achievements in Advanced Mathematics
Jian Qiao, Junjie Du, Zaixing Li
China University of Mining and Technology (Beijing), Beijing

Received: Oct. 1st, 2019; accepted: Oct. 14th, 2019; published: Oct. 21st, 2019

ABSTRACT
In the analysis of the higher mathematics scores of a 211 college students, the innovative ideas start from the relationship of students nesting in the teacher, instead of adopting the usual practice of students nesting in the class, using a two-level hierarchical linear model. Analysis has broken the limitations of ordinary regression models in analyzing data with nested structures. At the individual level, students’ higher mathematics grades are mainly influenced by their math scores and gender in college entrance examinations. Among them, the math scores of college entrance examinations have positive effects on higher mathematics scores, and the average scores of female students are higher than those of male students. At the teacher level, students’ higher mathematics scores are mainly influenced by the gender of the teacher. The average number of students taught by male teachers is higher than that of the female teachers.
Keywords:Hierarchical Linear Model, Higher Mathematics Scores, Data with Nested Structure, Individual Level, Group Level
高等数学成绩的分层线性回归分析
乔舰,杜俊洁,李再兴
中国矿业大学(北京),北京

收稿日期:2019年10月1日;录用日期:2019年10月14日;发布日期:2019年10月21日

摘 要
在对某211高校学生的高等数学成绩进行分析时,创新思路从学生嵌套于老师这一关系入手,而没有采用学生嵌套于班级这一通常做法,采用两水平的分层线性模型对其进行分析,打破了普通回归模型在分析具有嵌套结构数据的局限性。在个体水平上,学生的高等成绩主要受其高考数学成绩和性别的影响,其中高考数学成绩对高数成绩具有正效应,女同学的高数成绩平均高于男同学;在老师水平上,学生的高等数学成绩主要受老师性别的影响,男老师所教授学生的高数成绩平均高于女老师所教授的学生。
关键词 :分层线性模型,高等数学成绩,具有嵌套结构的数据,个体水平,组群水平

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
高等数学作为大学几乎所有专业的一门核心基础课,它的作用可谓是举足轻重。它不仅可以为其他课程的学习打下基础,还可以拓宽学生的思维,培养学生的逻辑能力,因此分析学生的高等数学成绩对大学制定学生培养计划至关重要。但是学生的数学学习能力不是天生就具备的,学生的高等数学成绩不仅受学生个体自身变量的影响,比如学生的智力水平、努力程度和其高考数学成绩等,也可能受任课老师的影响,一位同学被不同老师教授可能其的高数成绩会有所不同。
此时学生的高数成绩为具有嵌套结构的数据。学生与学生之间本来并无关系,但是当他们被同一位任课老师所教授后,他们之间便存在了某种联系,这种关系被叫做组内同质,而不同任课老师所教授的学生的高等数学成绩具有异质性。具有嵌套结构的数据不能满足普通回归分析所要求的独立性与方差齐性 [1] ,此时用普通回归处理具有嵌套结构的数据会产生错误,为了处理这一问题Lindley和Smith于1972年首先提出了分层线性模型 [2] 。本文基于分层线性模型的建立引入了可能对学生高等数学成绩有影响的变量,通过逐次引入并检验这些变量来定量分析各变量对学生高等数学成绩的影响。
2. 模型介绍
在此以两水平分层线性模型为例,
(2.1)
(2.2)
(2.3)
其中 表示在第j组中的第i个个体的水平1结局测量;其中 (N是总样本量),
(J是水平2的单位数)。式(2.1)是分析 变异的水平1方程。水平1截距 中的下标j表示水平1截距跨水平2单位变化,水平1回归系数 中的下标j表示水平1回归系数跨水平2单位变化。水平1变量 对 的效应随水平2单位而变化。与水平1随机回归系数 和 相对应的是两个水平2方程,在
这些方程中水平1随机回归系数变成了因变量。此时分层线性模型能够评估个体水平的解释变量与结局测量是如何受组群水平变量调节的,这就是分层线性模型的核心思想。在这里模型还假设水平1和水平2残差符合正态分布,而且水平1残差与水平2残差相互独立,这些假设可表述为:
3. 学生高等数学成绩建模分析
本文研究取自某211学校2014级不同学院两个学期的平均高数成绩和学生与任课老师的一些基本资料。根据一些常识与变量之间的相关性分析,本文初始选定自变量:学生的性别(标注为sex)、学生依老师中心化后的高考数学成绩(标注为cgaokao)、任课老师的性别(标注为xb)、任课老师的教龄(标注为jiaoling)、任课老师的职称(标注为zc),因变量为学生的高等数学成绩(标注为gaoshu)。现得到学生依老师中心化后的高等数学成绩与高考数学成绩的关系如图1:
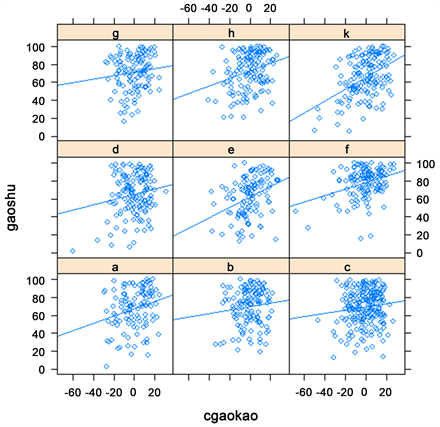
Figure 1. Regression analysis between the high scores of students in a 211 university and the math scores (centered) of the college entrance examination
图1. 某211大学学生的高数成绩与学生高考数学成绩(已中心化)之间的回归分析图
由图可知各位老师所教授学生的高数成绩与高考数学成绩之间的回归关系有显著不同,因此可初步得出运用分层线性模型是合理的。
1) 现在建立空模型,它是最简单的随机效应模型:
(3.1)
(3.2)
其中: :第j位老师所教授的第i位学生的高数成绩。 :第j位老师所教授学生的高数成绩均值与总均值 之间的差异。 :每位学生的高数成绩与老师所教授学生的高数成绩均值之间的差异。
根据检验得老师这一第2水平解释变量对学生的高考数学成绩与高数成绩之间的关系有显著影响,此时使用分层线性模型是合理的。
此时进行协方差参数估计得:水平1随机截距方差估计为 、水平1残差方差估计为 。组内相关系数ICC = 0.04,即学生的高数成绩中大约有4%的变异是由老师的不同引起的,每位老师所教授学生的高数成绩均值有显著不同。下面建立带宏观解释变量的随机截距模型。
2) 带宏观解释变量的随机截距模型:
(3.3)
(3.4)
其中: :第j位老师的教龄。xbj:第j位老师的性别,为虚拟变量,xb = 1表示为男性,xb = 0表示为女性。zcj:第j位老师的职称,为虚拟变量,zc = 1表示为副教授,zc = 0表示为讲师。
经过回归系数的显著性检验,老师的性别是显著的,而教龄与职称均不显著,因此最终将变量xb引入模型。得到最终的分层线性模型:
(3.5)
(3.6)
此时进行协方差估计得,模型中组内方差的估计值为 ,与空模型中组内方差的估计值 基本相同。组间方差的估计值为却从18.34下降到6.95。这说明了水平2解释变量xb能解释组间变异,但不能解释组内变异。此时组内相关系数ICC = 0.02。
模型解释的学生高数成绩组间变异可通过Raudenbush & Bryk方法或Snijders & Bosker方法进行估计 [3] 。此时采取Raudenbush & Bryk方法计算可得约有62.1%的学生高数成绩跨老师水平的变异可由组水平解释变量xb解释;采用Snijders & Bosker方法计算可得约有53.6%的学生高数成绩跨老师水平的变异可由组水平解释变量xb解释。
3) 现在考虑是否有个体因素会影响个人的高数成绩,因此将依老师中心化后的个体变量高考数学成绩和学生性别纳入模型2得到模型3:
(3.7)
(3.8)
经过回归系数显著性检验得中心化后的高考数学成绩与学生性别均显著,因此将两个变量都纳入分层线性模型。模型拟合统计量的结果表明将水平1的解释变量引入模型可以显著改善模型拟合度。
使用Raudenbush & Bryk方法,仅有7.5%的水平1变异可被模型解释,有66.9%的水平2变异可被模型解释;而用Snijders & Bosker方法则约有10%的水平1变异可被模型解释,有58.8%的水平2变异可被模型解释。在模型3中水平2解释方差为66.9%,而在模型2中为62.1%。这一结果说明了水平1解释变量既可在个体水平,也可在组群水平上影响结局变异。
4) 水平1解释变量斜率的随机性检验,建立模型4:
(3.9)
(3.10)
(3.11)
(3.12)
对回归系数的随机性进行显著性检验,得到结果依老师中心化后的学生高考数学成绩在老师与老师之间有显著性差别,即依老师中心化后的高考数学成绩的回归系数是随机回归系数。学生性别回归系数的随机性不显著,说明学生性别对学生依老师中心化后的高数成绩的影响不随老师的变化而变化。得到最终模型:
(3.13)
(3.14)
(3.15)
5) 考虑跨层交互作用,建立模型5:
(3.16)
(3.17)
(3.18)
经检验得学生的依老师中心化的高考数学成绩这一个体解释变量的效应并不受老师性别这一组群水平变量的影响。因此得到最终模型:
(3.19)
(3.20)
(3.21)
模型检验得检验结果,如表1所示:
Table 1. Test results of the final model
表1. 最终所建模型的检验结果
由检验结果可知,当学生依老师中心化后的高考数学成绩增加1分,则该学生的高数成绩平均增加0.38分;由于老师性别是虚拟变量(0-女性,1-男性),所以在保持其他条件不变的情况下,男老师所教授的学生的高数平均成绩比女老师所教授的学生的高数平均成绩高7.6;在其他条件不变的情况下,男同学的高数成绩在平均意义下比女同学低6.81。
4. 总结
在本次分析的学生的高数成绩与学生的高考数学成绩之间关系中,结果表明不同老师所教授学生的高数成绩差异显著。这一差异一方面是由学生依老师中心化后的高考数学成绩决定的,这是个体水平的解释变量,它体现的是学生个人的学习能力。另一方面是由不同大学老师存在差异而决定的,这是组群水平的解释变量。具体分析结果表明:1) 在其它条件不变的情况下,男老师对学生高数成绩影响程度较女老师更大。因此在进行教师招聘的过程中应该协调好男女教师的比例,不应让比例失衡,以此来降低由老师性别差异对学生高等数学成绩的影响。2) 在其它条件不变的情况下,女同学的高数成绩普遍高于男同学。因此老师应该更加关注男同学的学习,同时也可以搭配男女互助学习小组,让女同学带动男同学的学习,共同进步。老师也可以加强男同学的出勤率考察,以此来督促男同学学习。3) 在其它条件不变的情况下,拥有更好高考数学成绩的同学普遍拥有更高的高数成绩。因此在各高校招生时我们不仅需对高考总分进行划线,也应对高考数学成绩有基本要求。同时老师也可以对基础薄弱的同学适当增加帮扶,例如上课时多抽点基础薄弱的同学回答问题,以此激励他们进步。
基金项目
本文受国家自然科学基金(项目编号:11671398)支持。
文章引用
乔 舰,杜俊洁,李再兴. 高等数学成绩的分层线性回归分析
Hierarchical Linear Regression Analysis of Achievements in Advanced Mathematics[J]. 统计学与应用, 2019, 08(05): 760-765. https://doi.org/10.12677/SA.2019.85086
参考文献
- 1. 何晓群, 刘文卿. 应用回归分析[M]. 第4版. 北京: 中国人民大学出版社, 2011: 18-20.
- 2. Stephen W. Raudenbush, Anthony S. Bryk. 分层线性模型: 应用与数据分析方法[M]. 第2版. 北京: 社会科学文献出版社, 2007: 15-21.
- 3. 王济川, 谢海义, 姜宝法. 多层统计分析模型: 方法与应用[M]. 第2版. 北京: 高等教育出版社, 2008: 1-73.
