Advances in Applied Mathematics
Vol.06 No.02(2017), Article ID:19927,7
pages
10.12677/AAM.2017.62016
Disjoint Subgraphs with Specified Properties in Graphs
Yihua Wang1, Shuo Li2, Xiaoning Yi1
1School of Mathematics, Shandong University, Jinan Shandong
2Department of Mathematics, Changji University, Changji Xinjiang

Received: Feb. 26th, 2017; accepted: Mar. 18th, 2017; published: Mar. 21st, 2017

ABSTRACT
Let G be a graph of order n with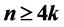 , where k is a positive integer. Suppose that
, where k is a positive integer. Suppose that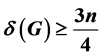 , then the partition of G can be
, then the partition of G can be 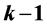 vertex disjoint 4-cliques and a chordal cycle, where the degree of vertexes in this chordal cycle is equal or greater than 3 or 4.
vertex disjoint 4-cliques and a chordal cycle, where the degree of vertexes in this chordal cycle is equal or greater than 3 or 4.
Keywords:Vertex-Disjoint, 4-Cliques, Chordal Cycle

图中具有指定性质的不交子图
王怡华1,李硕2,衣晓宁1
1山东大学数学学院,山东 济南
2昌吉学院数学系,新疆 昌吉

收稿日期:2017年2月26日;录用日期:2017年3月18日;发布日期:2017年3月21日

摘 要
令G是一个顶点数为n的简单图,满足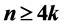 ,k是任意正整数。假设
,k是任意正整数。假设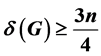 ,则图G可划分成
,则图G可划分成 个点不交的4-团和一个弦圈,使得弦圈上点的度大于等于3或4。
个点不交的4-团和一个弦圈,使得弦圈上点的度大于等于3或4。
关键词 :点不交,4-团,弦圈

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文中的图都为简单图。令 是一个简单图,图G的顶点数和边数分别为
是一个简单图,图G的顶点数和边数分别为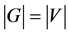 和
和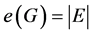 。图G中的一列子图称为独立的如果任意两个子图在G中没有公共点。若
。图G中的一列子图称为独立的如果任意两个子图在G中没有公共点。若 和
和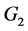 在G中没有公共点,我们定义
在G中没有公共点,我们定义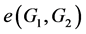 为
为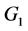 和
和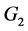 之间的边数。假设H是G的子图并且
之间的边数。假设H是G的子图并且 ,
,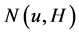 表示u在H中的邻点,并且
表示u在H中的邻点,并且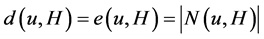 。对G中的子图U,令
。对G中的子图U,令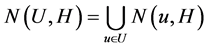 ,且
,且 表示
表示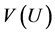 的导出子图。
的导出子图。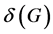 表示图G的最小度。同时,我们定义
表示图G的最小度。同时,我们定义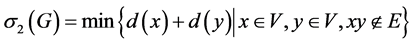 。我们用
。我们用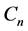 和
和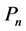 分别表示顶点数为n的圈和路。路P称为图G的支撑路,如果路P覆盖图G中所有点。团是指G的一个完全子图,若一个团中包含的顶点数为k,则称其为k-团。
分别表示顶点数为n的圈和路。路P称为图G的支撑路,如果路P覆盖图G中所有点。团是指G的一个完全子图,若一个团中包含的顶点数为k,则称其为k-团。
1963年,Erdös提出了一个关于图中包含k个点不交团的猜想。
猜想1 [1] 设G是一个顶点数为n的图。如果 ,s和k为正整数且
,s和k为正整数且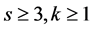 。假设
。假设 ,那么G含有k个点不交的
,那么G含有k个点不交的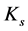 ,即
,即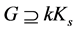 。
。
1970年,Hajnal和Szemeréd证明了该猜想,但他们的证明非常难懂,并且证明过程也非常复杂。1978年,Bollobós关于此猜想给出了简单的证明。当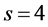 时,为如下定理。
时,为如下定理。
定理1.1 [2] 设G是一个顶点数为n的图。如果 ,k为正整数。假设
,k为正整数。假设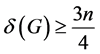 ,那么G含有k个独立的4-团。
,那么G含有k个独立的4-团。
关于图中点不交的圈问题,1963年,Corrádi和Hajanal证明了下面定理。
定理1.2 [3] 设G是一个顶点数为n的图。如果 ,k为正整数。假设
,k为正整数。假设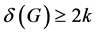 ,那么G含有k个独立的圈。
,那么G含有k个独立的圈。
最近Wang考虑了每个连通分支为固定大小的2-因子问题。
定理1.3 [4] 设G是一个顶点数为n的图。如果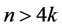 ,k为正整数。假设
,k为正整数。假设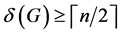 ,那么G有含有k个独立的圈的2-因子,其中k-1个为4-圈。
,那么G有含有k个独立的圈的2-因子,其中k-1个为4-圈。
本文将定理1.3的4-圈推广到4-团,得到如下命题。
定理1.4 设G是一个顶点数为n的图。如果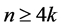 ,k为正整数。假设
,k为正整数。假设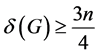 ,那么G含有k-1个独立的4-团和一个弦圈,弦圈上的度大于等于3或4。
,那么G含有k-1个独立的4-团和一个弦圈,弦圈上的度大于等于3或4。
在证明定理1.4之前,我们先引入下面几个引理。
2. 引理
引理2.1 设G是一个顶点数为n的图。如果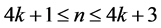 ,k为正整数。假设
,k为正整数。假设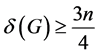 ,那么G含有k个独立的4-团。
,那么G含有k个独立的4-团。
证明:
假设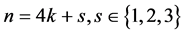 。令S为G中任意s个点的集合,则
。令S为G中任意s个点的集合,则 。因为最小度为整数且
。因为最小度为整数且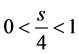 ,所以
,所以 。又因为
。又因为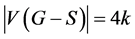 ,由定理1.1可知,图G含有k个点不交的4-团。□
,由定理1.1可知,图G含有k个点不交的4-团。□
引理2.2 令T为图G中的一个4-团并且令 和
和 为图G中不在T上的两个不相邻的点。如果
为图G中不在T上的两个不相邻的点。如果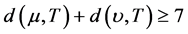 ,那么
,那么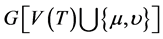 包含一个4-团
包含一个4-团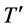 和一条边e,使得
和一条边e,使得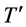 和e是不交的并且e恰好与
和e是不交的并且e恰好与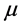 和
和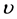 中的一点相连。
中的一点相连。
证明:假设 。因为
。因为 ,则设
,则设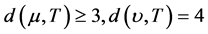 ,所以点
,所以点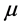 在T中的邻点中至少有三个,不妨设为
在T中的邻点中至少有三个,不妨设为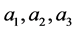 。
。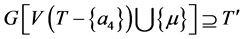 与边
与边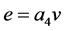 是不交的。□
是不交的。□
引理2.3 [5] 如果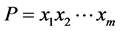 为G中的一条路,
为G中的一条路,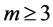 ,满足
,满足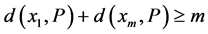 ,那么G含有一个圈C 满足
,那么G含有一个圈C 满足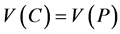 。另外,对于G中任意两个不相邻的点x,y,如果
。另外,对于G中任意两个不相邻的点x,y,如果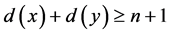 ,那么G是哈密顿连通的。
,那么G是哈密顿连通的。
令G是一个顶点数为n的图,定义G的(n+1)-闭包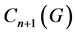 为从G中递归地连接每对度和至少为
为从G中递归地连接每对度和至少为 的不相邻的两个点所得到的图。
的不相邻的两个点所得到的图。
引理2.4 [6] 令G是一个顶点数为n的图,如果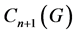 是完全图,那么G是哈密顿连通的。
是完全图,那么G是哈密顿连通的。
引理2.5 [4] 假定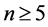 且
且 。那么对于任意
。那么对于任意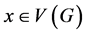 ,G含有一个4-圈Q满足
,G含有一个4-圈Q满足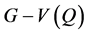 有一条起始于x的哈密顿路。
有一条起始于x的哈密顿路。
3. 定理的证明
令G是一个顶点数为n的图,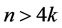 ,k为正整数,满足条件
,k为正整数,满足条件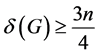 。因为G有一个哈密顿圈,当
。因为G有一个哈密顿圈,当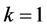 时定理1.4成立。假设
时定理1.4成立。假设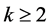 ,令
,令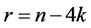 。为了证明,我们首先证明下列的断言。
。为了证明,我们首先证明下列的断言。
断言3.1 G包含k个独立的4-团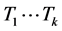 使得
使得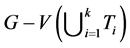 有一条哈密顿路P。并且当
有一条哈密顿路P。并且当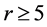 时,对任意
时,对任意 。
。
证明:我们首先证明断言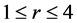 的情况。由引理2.1,
的情况。由引理2.1,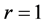 时,断言是平凡的。如果
时,断言是平凡的。如果 ,那么
,那么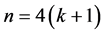 。由定理1.1,G包含
。由定理1.1,G包含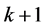 个独立的4-团。所以当
个独立的4-团。所以当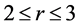 时,由引理2.1,G包含k个独立的4-团
时,由引理2.1,G包含k个独立的4-团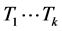 。令
。令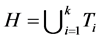 且
且 。我们选择
。我们选择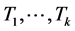 使得
使得
(a) D中的路尽可能的长
当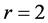 时,我们断言D包含一条边。否则,令
时,我们断言D包含一条边。否则,令 为D中不相邻的两点。则
为D中不相邻的两点。则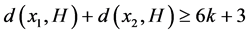 ,因此存在
,因此存在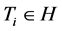 使得
使得 。由引理2.2,
。由引理2.2,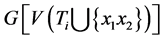 包含相互独立的一个4-团和一条边。这与选择(a)矛盾。这也证明断言对
包含相互独立的一个4-团和一条边。这与选择(a)矛盾。这也证明断言对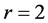 时成立。
时成立。
假定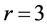 。令
。令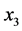 为D中另外一点,且
为D中另外一点,且 。所以
。所以 。则存在
。则存在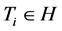 ,使得
,使得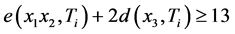 。 假设
。 假设 且
且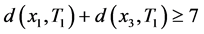 。当
。当 时,不妨设
时,不妨设 。因为D中不含长度为3的路,所以点
。因为D中不含长度为3的路,所以点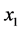 与
与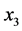 不相邻。由引理2.2,则
不相邻。由引理2.2,则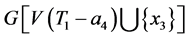 包含一个4-团并且
包含一个4-团并且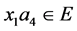 ,产生一条路
,产生一条路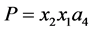 ,矛盾。因此
,矛盾。因此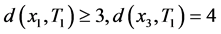 。不妨设
。不妨设 ,类似地,
,类似地,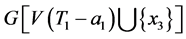 包含一个4-团并且
包含一个4-团并且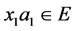 ,产生一条路
,产生一条路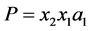 ,矛盾。证明断言对
,矛盾。证明断言对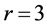 时成立。
时成立。
现在假定 。首先我们证明下列命题成立。
。首先我们证明下列命题成立。
(*)假定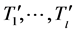 是G中l个独立的4-团且
是G中l个独立的4-团且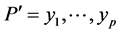 是
是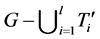 的一条支撑路。则存在
的一条支撑路。则存在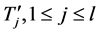 ,使得
,使得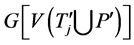 包含一条支撑路。
包含一条支撑路。
如果不是,则 。另外,我们可以假设
。另外,我们可以假设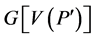 包含一个哈密顿圈。否则,
包含一个哈密顿圈。否则,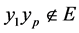 ,则
,则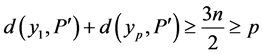 。由引理2.3,
。由引理2.3,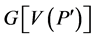 含有一个哈密顿圈。因为G是连通的,所以存在一个4-团
含有一个哈密顿圈。因为G是连通的,所以存在一个4-团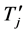 使得
使得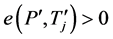 。因此,
。因此,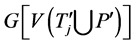 包含一条支撑路。
包含一条支撑路。
令s为正整数,使得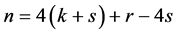 且
且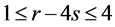 。由引理2.1和当
。由引理2.1和当 时的结论,我们可以找到
时的结论,我们可以找到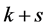 个点不交的4-团,设为
个点不交的4-团,设为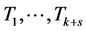 ,和一条长度为
,和一条长度为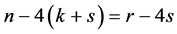 的路。由
的路。由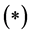 递归可知,我们得到相互独立的k个4-团和一条顶点数为r的路P。
递归可知,我们得到相互独立的k个4-团和一条顶点数为r的路P。
现在我们讨论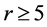 时哈密顿路P上点的度。
时哈密顿路P上点的度。
由D中顶点数为r的哈密顿路P的构造过程可知,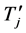 中与
中与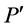 关联的点度大于等于4,与下一个4-团关联的点度大于等于4,其余两个点度大于等于3。
关联的点度大于等于4,与下一个4-团关联的点度大于等于4,其余两个点度大于等于3。
接下来讨论哈密顿路P中其余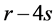 个点的度,
个点的度,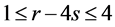 。
。
当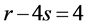 时,由定理1.1可知,G中包含
时,由定理1.1可知,G中包含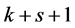 个4-团,则这四个点可以组成一个4-团,设为
个4-团,则这四个点可以组成一个4-团,设为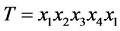 ,从
,从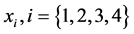 中任选两点,不妨设为
中任选两点,不妨设为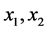 。则
。则
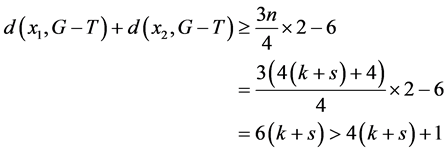
因此在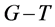 的
的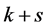 个4-团中存在一个4-团
个4-团中存在一个4-团 ,使得
,使得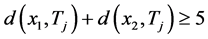 ,则
,则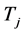 中至少存在两个不同的点与
中至少存在两个不同的点与 和
和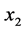 相连,设两条关联的边为
相连,设两条关联的边为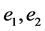 。因此
。因此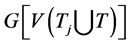 包含一个哈密顿圈C,且在C中
包含一个哈密顿圈C,且在C中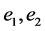 关联的四个点度大于等于4,非关联的点度大于等于3。 若
关联的四个点度大于等于4,非关联的点度大于等于3。 若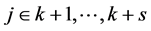 ,则在哈密顿路P上这四个点中有两个度大于等于4,两个大于等于3。若
,则在哈密顿路P上这四个点中有两个度大于等于4,两个大于等于3。若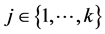 ,则让
,则让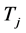 替换
替换 中任意4-团
中任意4-团 ,可以得到上述相同结果。
,可以得到上述相同结果。
当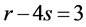 时,设为
时,设为 。如果点
。如果点 与
与 不相邻,则
不相邻,则
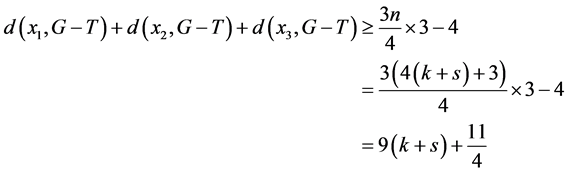
所以在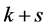 个4-团中存在一个4-团
个4-团中存在一个4-团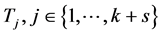 ,使得
,使得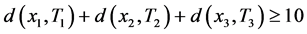 ,则
,则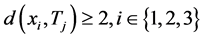 。因此,点
。因此,点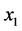 与
与 在
在 中的度大于等于3,点
中的度大于等于3,点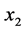 在
在 中的度大于等于4。若
中的度大于等于4。若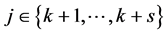 ,则在哈密顿路P上这三个点中有两个度大于等于3,一个大于等于4。否则,则让
,则在哈密顿路P上这三个点中有两个度大于等于3,一个大于等于4。否则,则让 替换
替换 中任意4-团
中任意4-团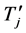 ,可以得到上述相同结果。如果点
,可以得到上述相同结果。如果点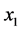 与
与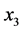 相邻,这三个点可以组成三角形,设为
相邻,这三个点可以组成三角形,设为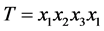 。则
。则
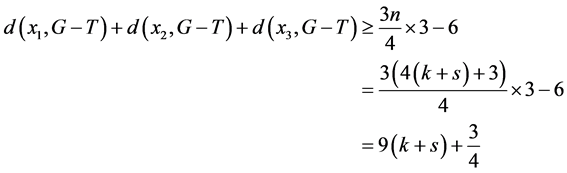
所以在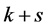 个4-团中存在一个4-团
个4-团中存在一个4-团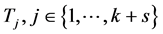 ,使得
,使得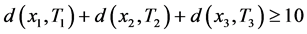 。因此,与点
。因此,与点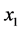 与
与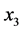 不相邻的情况类似,点
不相邻的情况类似,点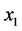 ,
,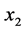 与
与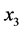 在哈密顿路P上度大于等于4。
在哈密顿路P上度大于等于4。
当 时,这两个点组成路T,设
时,这两个点组成路T,设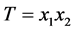 。则
。则

所以在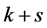 个4-团中至少存在一个4-团
个4-团中至少存在一个4-团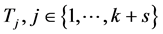 ,使得
,使得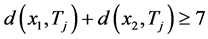 ,则
,则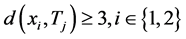 。因此,点
。因此,点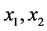 在
在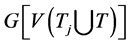 中的度大于等于4。若
中的度大于等于4。若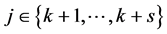 ,则这两点在哈密顿路P上度大于等于4。否则,则让
,则这两点在哈密顿路P上度大于等于4。否则,则让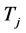 替换
替换 中任意4-团
中任意4-团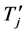 ,可以得到上述相同结果。
,可以得到上述相同结果。
当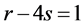 时,这个点设为x。则
时,这个点设为x。则
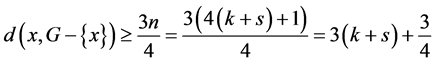
所以在 个4-团中至少存在一个4-团
个4-团中至少存在一个4-团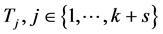 ,使得
,使得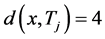 。因此点x在
。因此点x在 中的度大于等于5。若
中的度大于等于5。若 ,则这两点在哈密顿路P上度大于等于5。否则,则让
,则这两点在哈密顿路P上度大于等于5。否则,则让 替换
替换 中任意4-团
中任意4-团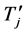 ,可以得到上述相同结果。
,可以得到上述相同结果。
因此断言3.1成立。□
令 ,P为D中的一条哈密顿路,不妨设两个端点为
,P为D中的一条哈密顿路,不妨设两个端点为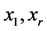 。若
。若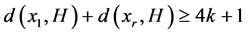 ,则存在
,则存在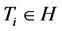 ,使得
,使得 ,设
,设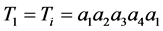 。由此可知
。由此可知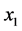 与
与 在
在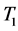 中至少有一个共同点,设为
中至少有一个共同点,设为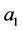 ,则
,则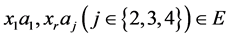 。因此,
。因此,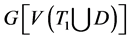 是哈密顿的。即图G含有
是哈密顿的。即图G含有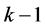 个4-团和一个哈密顿圈。由断言3.1可知,当
个4-团和一个哈密顿圈。由断言3.1可知,当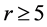 时,这个哈密顿圈上点的度大于等于3或4。下面讨论当
时,这个哈密顿圈上点的度大于等于3或4。下面讨论当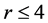 时哈密顿圈上的度。若
时哈密顿圈上的度。若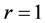 ,设这个点为x ,
,设这个点为x ,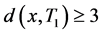 是平凡的,即所得哈密顿圈上点的度大于等于3或4。若
是平凡的,即所得哈密顿圈上点的度大于等于3或4。若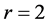 ,
,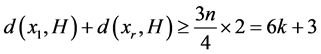 ,则存在
,则存在 ,使得
,使得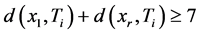 ,因此
,因此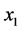 和
和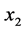 在
在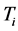 中至少有三个邻点,即哈密顿圈上点的度大于等于3或4。若
中至少有三个邻点,即哈密顿圈上点的度大于等于3或4。若 ,设路P上的三个点分别为
,设路P上的三个点分别为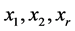 ,因为
,因为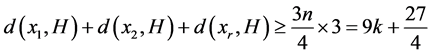 ,所以存在
,所以存在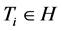 ,使得
,使得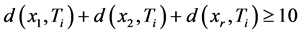 ,则
,则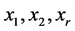 在
在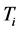 中至少有三个邻点,即哈密顿圈上点的度大于等于3或4。若
中至少有三个邻点,即哈密顿圈上点的度大于等于3或4。若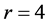 ,由断言3.1可知,P为一个4-团,即哈密顿圈上点的度大于等于3或4。综上,当
,由断言3.1可知,P为一个4-团,即哈密顿圈上点的度大于等于3或4。综上,当 ,主要定理得证。
,主要定理得证。
否则,
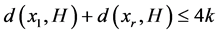 (1)
(1)
则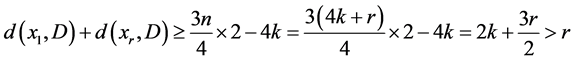 。由引理2.3,D含有一个圈C,使得
。由引理2.3,D含有一个圈C,使得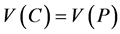 。
。
断言3.2 如果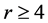 ,那么
,那么 ,对于任意
,对于任意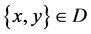 且
且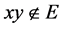
证明:首先假定D中的每条哈密顿路的端点是邻接的。令P为D中的一条哈密顿路并且令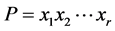 。我们假定
。我们假定 。假设
。假设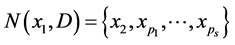 ,对于任意
,对于任意 ,存在一条哈密顿路
,存在一条哈密顿路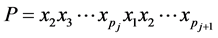 。由假设可知
。由假设可知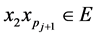 ,因为
,因为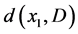 的极大性,我们得到
的极大性,我们得到 。 相同地,
。 相同地,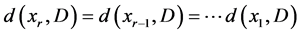 。则D是一个正则图。
。则D是一个正则图。
令 ,则
,则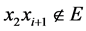 。否则D有一条哈密顿路
。否则D有一条哈密顿路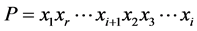 ,由假设可知
,由假设可知 产生矛盾。因此
产生矛盾。因此
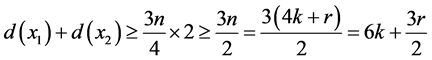
由(1)可得, ,则
,则 。因为D为G的正则子图,所以
。因为D为G的正则子图,所以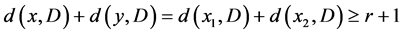 对于任意
对于任意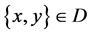 。如果D中存在一条哈密顿路使得它的两个端点u,v是非邻接的,我们有
。如果D中存在一条哈密顿路使得它的两个端点u,v是非邻接的,我们有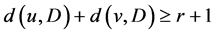 。令
。令 为D中的一个哈密顿圈并且假定
为D中的一个哈密顿圈并且假定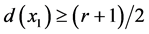 。现在我们构造
。现在我们构造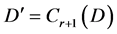 。假定
。假定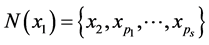 并且
并且 。我们可以找到一条哈密顿路
。我们可以找到一条哈密顿路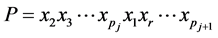 ,对任意的
,对任意的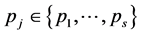 。因此,我们得到一条以
。因此,我们得到一条以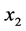 为其中一个端点的
为其中一个端点的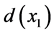 的哈密顿路。如果
的哈密顿路。如果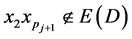 ,则
,则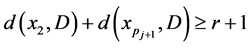 。在
。在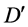 中我们连接
中我们连接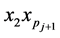 ,所以我们有
,所以我们有 。相同地,
。相同地, 。因此
。因此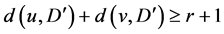 ,对于
,对于 中的任意一对
中的任意一对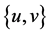 。由定义可知
。由定义可知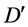 是一个完全图。由引理2.4,D是哈密顿连通的,也就是说对于D中的每对点
是一个完全图。由引理2.4,D是哈密顿连通的,也就是说对于D中的每对点 ,都存在一条以u,v为端点的哈密顿路。因此,对于D中的每对非相邻的点
,都存在一条以u,v为端点的哈密顿路。因此,对于D中的每对非相邻的点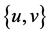 ,
, 成立。
成立。
现在我们证明主要定理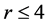 的情形,我们选择k个点不交的4-团
的情形,我们选择k个点不交的4-团 和D中一条哈密顿路。
和D中一条哈密顿路。
如果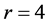 ,由断言3.2可知,D为一个4-团,设为
,由断言3.2可知,D为一个4-团,设为 ,从
,从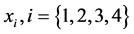 中任选两点,不妨设为
中任选两点,不妨设为 。则
。则

因此在H中存在一个4-团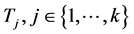 ,使得
,使得 ,则
,则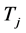 中至少存在两个不同的点与T中两点相连,设两条关联的边为
中至少存在两个不同的点与T中两点相连,设两条关联的边为 。因此
。因此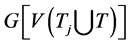 包含一个哈密顿圈C,且在C中
包含一个哈密顿圈C,且在C中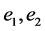 关联的四个点度大于等于4,非关联的点度大于等于3。
关联的四个点度大于等于4,非关联的点度大于等于3。
如果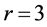 ,D为一个三角形,设为
,D为一个三角形,设为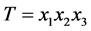 。则
。则
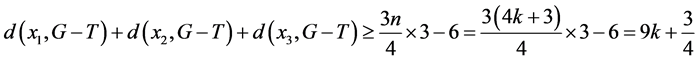
所以在H中存在一个4-团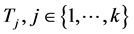 ,使得
,使得 ,
,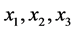 在
在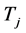 中至少存在两个邻点。显然
中至少存在两个邻点。显然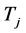 中存在三个不同的点分别为与T中三点相连,对应的边设为
中存在三个不同的点分别为与T中三点相连,对应的边设为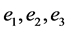 。因此
。因此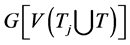 包含一个哈密顿圈C,且在C中T中的三个点度大于等于3,
包含一个哈密顿圈C,且在C中T中的三个点度大于等于3,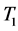 中的与
中的与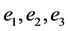 关联的三个点度大于等于4,剩余一个点度大于等于3。
关联的三个点度大于等于4,剩余一个点度大于等于3。
如果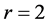 ,这两个点组成路P,设
,这两个点组成路P,设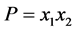 。则
。则
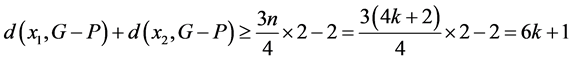
在H中存在一个4-团 ,使得
,使得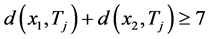 ,则
,则 。即P中两点在
。即P中两点在 中的邻点至少有三个为共同点,对应的边组成的集合设为E。因此
中的邻点至少有三个为共同点,对应的边组成的集合设为E。因此 包含一个哈密顿圈C,且在C中P中的两个点度大于等于4,
包含一个哈密顿圈C,且在C中P中的两个点度大于等于4,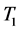 中的与E中的边关联的三个点度大于等于5,剩余一个点度大于等于4。
中的与E中的边关联的三个点度大于等于5,剩余一个点度大于等于4。
如果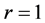 ,D为一个点,设为x。则
,D为一个点,设为x。则
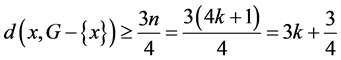
在H中至少存在一个4-团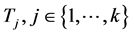 ,使得
,使得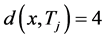 。因此
。因此 包含一个哈密顿圈C,且在C中点的度为4。
包含一个哈密顿圈C,且在C中点的度为4。
当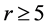 时。令P为D的一条哈密顿路,其中一个端点为u,使得
时。令P为D的一条哈密顿路,其中一个端点为u,使得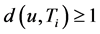 ,对于某些
,对于某些 。不失一般性,
。不失一般性,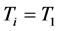 。
。
由引理2.5,D中有一个4-圈Q使得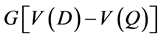 含有一条起始于u的哈密顿路
含有一条起始于u的哈密顿路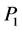 。因为
。因为 ,所以
,所以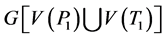 有一条哈密顿路
有一条哈密顿路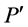 。 因为D是哈密顿的,我们可以选择在Q与
。 因为D是哈密顿的,我们可以选择在Q与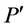 中两条互不相交的边
中两条互不相交的边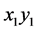 和
和 。我们称
。我们称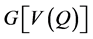 有一条从
有一条从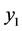 到
到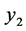 的支持路。否则,假设
的支持路。否则,假设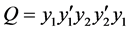 。则
。则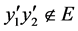 且
且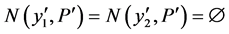 。由
。由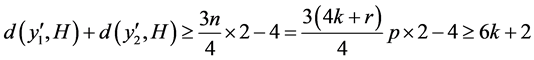 ,则存在
,则存在 ,使得
,使得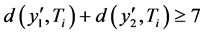 。由断言3.2,D是哈密顿连通的,则在
。由断言3.2,D是哈密顿连通的,则在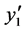 与
与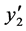 之间存在一条D中的哈密顿路并且
之间存在一条D中的哈密顿路并且 是哈密顿的,产生矛盾。用Q代替
是哈密顿的,产生矛盾。用Q代替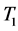 ,则断言3.2对
,则断言3.2对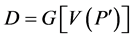 仍成立。那么D是哈密顿连通的,存在一条以
仍成立。那么D是哈密顿连通的,存在一条以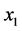 和
和 为端点的哈密顿路。因此
为端点的哈密顿路。因此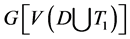 是哈密顿的,产生矛盾。
是哈密顿的,产生矛盾。
现在我们讨论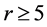 时弦圈C的结构。由定理证明中弦圈C的构造过程可知,
时弦圈C的结构。由定理证明中弦圈C的构造过程可知,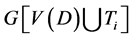 包含哈密顿圈,即所构造的弦圈C。在C上
包含哈密顿圈,即所构造的弦圈C。在C上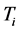 中与D中哈密顿路
中与D中哈密顿路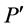 关联的点度大于等于4,其余两点度大于等于3。弦圈C中其它点的度的情况断言3.1已证。□
关联的点度大于等于4,其余两点度大于等于3。弦圈C中其它点的度的情况断言3.1已证。□
基金项目
国家自然科学基金资助项目(11671232)。新疆自然科学基金面上项目(2016D01C004)。
文章引用
王怡华,李硕,衣晓宁. 图中具有指定性质的不交子图
Disjoint Subgraphs with Specified Properties in Graphs[J]. 应用数学进展, 2017, 06(02): 139-145. http://dx.doi.org/10.12677/AAM.2017.62016
参考文献 (References)
- 1. Erdös, P. (1967) Extremal Problems in Graph Theory. In: Harary, F., Ed., A Seminar in Graph Theory, Holt, Rinehart and Winston, 54-56.
- 2. Bollobás, B. (2004) Extremal Graph Theory. Courier Corporation.
- 3. Corradi, K. and Hajnal, A. (1963) On the Maximal Number of Independent Circuits in a Graph. Acta Mathematica Hungarica, 14, 423-439. https://doi.org/10.1007/BF01895727
- 4. Wang, H. Covering a Graph with Cycles of Lengths at Least 4.
- 5. Ore, O. (1960) Note on Hamilton Circuits. The American Mathematical Monthly, 67, 55. https://doi.org/10.2307/2308928
- 6. Chartrand, G., Lesniak, L. and Zhang, P. (2010) Graphs & Digraphs. CRC Press.