Advances in Applied Mathematics
Vol.
10
No.
03
(
2021
), Article ID:
40958
,
9
pages
10.12677/AAM.2021.103074
基于近似贝叶斯方法的AR(p)模型参数估计问题研究
陈博文1,夏莉1,2
1广东财经大学统计与数学学院,广东 广州
2广东财经大学大数据与教育统计应用实验室,广东 广州

收稿日期:2021年2月11日;录用日期:2021年3月8日;发布日期:2021年3月16日

摘要
文章选用近似贝叶斯估计方法和最小二乘法对AR(p)模型进行参数估计,通过RStudio软件产生仿真AR(2)模型数据,比较这两种方法对参数估计的准确性。最后通过实例对这两种参数估计方法的效果进行验证。
关键词
AR(p)模型,近似贝叶斯方法,最小二乘法
Research on Parameter Estimation of AR(p) Model Based on Approximate Bayesian Computation
Bowen Chen1, Li Xia1,2
1School of Statistics and Mathematics, Guangdong University of Finance & Economics, Guangzhou Guangdong
2Big Data and Educational Statistics Application Laboratory, Guangzhou Guangdong

Received: Feb. 11th, 2021; accepted: Mar. 8th, 2021; published: Mar. 16th, 2021

ABSTRACT
In this paper, approximate Bayesian computation and least square method are used to estimate the parameters of AR(p) model. The simulation AR(2) model data are generated by RStudio software, and the accuracy of parameter estimate is compared between the two methods. Finally, the effectiveness of the two parameter estimation methods is verified by examples.
Keywords:AR(p) Model, Approximate Bayesian Computation, Least Square Method

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着社会的不断发展,对经济、金融数据的分析成为了研究经济变化趋势必不可少的环节,然而经济、金融领域方面的数据一般都是时间序列数据,我们可以使用时间序列模型对这些数据进行建模分析,而AR(p)模型则是时间序列模型中较为常见的模型。
研究AR(p)模型时,主要从数据是否存在异常值角度出发。当时间序列数据具有异常值时,王玉丽等将抗差理论引入到AR(p)模型的参数估计中,在实时洪水预报的误差修正中,利用抗差理论估计AR(p)模型的参数,抵御异常观测值对参数估计的影响,以保证实时洪水的预报精度 [1]。王志坚 [2] [3] 等运用FQn统计量、Hampel权函数对传统自相关函数进行改动,构建AR(p)模型的稳健估计算法,以克服离群值的影响,并对此方法进行了模拟和实证分析。当数据不存在异常值时,对AR(p)模型参数估计的方法也就会变得不一样。朱慧明等研究了正态-Gamma共轭先验分布下AR(p)模型的贝叶斯推断理论,从而进行模型参数的估计 [4]。章敏,李在兴分析了一阶自回归模型中模型相关参数估计方法(矩估计和最小二乘估计)的无偏性 [5]。彭毳鑫等讨论了条件矩约束下自回归模型参数的估计问题,利用经验似然方法,给出了条件矩约束下自回归模型参数的估计 [6]。陈阳等证明了Adaptive Lasso在AR(p)模型定阶和参数估计上有良好的性质 [7]。谢琍 [8] 等对文献 [7] 进行了进一步研究,提出了将Lasso等三种惩罚进行惩罚效果的比较,然后利用惩罚最小二乘法进行参数估计。这些学者从多个方面对AR(p)模型问题进行了研究,提出了很多好的方法。
自从1984年Rubin [9] 首次提出近似贝叶斯的基本思想后,尤其是近些年来,该算法被应用到各个领域中,钱瑾基于合成似然的近似贝叶斯方法对人口基因模型进行研究 [10];张晨把近似贝叶斯方法应用在流感病毒传染模型中进行分析研究 [11]。张岚,钱夕元将近似贝叶斯方法应用在排队模型参数估计问题上 [12]。近似贝叶斯计算作为一种复杂模型参数估计的方法被广泛应用到各类模型的参数估计问题中;如:黄鹂 [13]、周双酉 [14] 分别将近似贝叶斯方法应用在分层二项分布、广义线性回归模型中进行参数估计研究。
因此,本文应用近似贝叶斯方法来对AR(p)模型进行研究。先介绍用近似贝叶斯方法对AR(p)模型进行参数估计的算法,然后再进行数据模拟实验对参数估计效果进行验证,最后应用该方法来分析金融时间序列数据。
2. 模型介绍
2.1. AR(p)模型
如果随机变量序列 ,满足 , ;其中 ,随机误差项 相互独立且都服从正态分布 ,则称 为 阶自回归过程,即AR(p)模型,其中 为模型的自回归系数,p为模型的阶。若自回归系数 的特征方程
的根都落在单位圆外,则称 为平稳序列过程。
2.2. AR(p)模型参数的最小二乘估计
模型的自相关函数与自回归参数满足Yule-Walker方程 [15]:
用样本自相关函数 代替 ,便得到参数估计值
参数 的最小二乘估计为Yule-Walker估计, 的最小二乘估计为 [16]:
其中 为 的最小二乘估计。
2.3. AR(p)模型参数的近似贝叶斯估计
2.3.1. 近似贝叶斯基本思想
近似贝叶斯计算(Approximate Bayesian Computation, ABC)是一种基于模拟采样和计算机仿真的方法,最早由Pritchard等人于1999年提出 [17]。它利用贝叶斯统计中后验分布的性质以及计算机模拟抽样的方法解决后验分布计算困难的问题,绕开了对似然函数的直接计算。ABC方法的核心思想是基于参数的先验分布采样得到一个待选参数,用待选参数值代入模型通过模拟仿真产生一组模拟数据集,并将模拟数据集与观测数据集作比较,观测两个数据集的差异程度。当模拟数据集与观测数据集的差距“足够小”时,我们可以接受该待选参数作为参数真实后验分布的一个采样,进而获得待估参数的后验分布,从而利用这个后验分布去估计参数的后验均值。
2.3.2. ABC拒绝算法
ABC方法的最基本形式是ABC拒绝算法。步骤如下:
给定观测数据集Y,模型Q,先验分布 ,距离函数 ,容差阈值 。
1) 从先验分布 中生成一个 ,作为一个样本;
2) 由 根据模型Q生成模拟数据集 ;
3) 计算 ,若 ,则接受 ,令 并记录下来;反之则拒绝 ;
4) 重复步骤1)-3),直到有n个样本被接受;
5) 计算参数 的估计值 ,。
通过ABC拒绝算法我们可以得到n个来自近似后验分布 的样本,距离函数和容差阈值选取恰当的情况下,我们可以用这n个样本所获得的分布作为真实后验分布 的近似,在此基础上进行统计推断。
2.3.3. AR(p)模型参数的ABC估计算法
给定已知的AR(p)模型观测数据 ,参数 的先验分布 ,,容差阈值 。
生成n组 的样本步骤如下:
1) 计算 的自相关系数 。
2) 根据先验分布 生成一组 。
3) 计算 特征方程的根 。若 ,则到步骤(4);否则退回步骤(2)。
4) 根据 , 生成AR(p)模型数据 。
5) 计算数据 的自相关系数 。
6) 计算 。若 ,则接受 作为一组样本,令 并记录下来;反之则拒绝 。
7) 重复步骤2)-6),直到有n组样本被接受;
8) 计算参数 的估计值 ,。
我们通过上面步骤得到参数 的估计值 .接着计算参数 的步骤为:
已知的AR(p)模型观测数据 ,参数 的先验分布 ,,容差阈值 。
1) 计算 的自相关系数 。
2) 根据先验分布 生成一个 。
3) 根据 , 生成AR(p)模型数据 。
4) 计算数据 的自相关系数 。
5) 计算 。若 ,则接受 ,令 并记录下来;反之则拒绝 。
6) 重复步骤(2)-(5),直到有n个 被接受;
7) 计算参数 的估计值 ,。
3. 模拟验证
本次模拟针对AR(2)模型,应用最小二乘法和近似贝叶斯方法对参数估计的效果进行验证。
本次验证的模型为:
其中随机误差项 相互独立,服从正态分布 。此处模拟的模型可以通过单位根检验,保证了生成序列的平稳性。此处 取值为500。
RStudio软件中arima函数便是使用最小二乘法来估计参数的,因此我们直接调用arima函数去估计AR(2)模型的参数。
同时我们使用RStudio软件直接对AR(2)模型参数的ABC估计算法直接进行编程去求参数估计的结果。在AR(2)模型参数的ABC估计中,参数 的先验分布取: 上的均匀分布,从P中取值的参数 才能使生成的模拟数据达到平稳序列要求;令 ,其中 的先验分布取Ga(1, 2)。
模拟实验得到参数 , 的频率分布直方图和后验分布密度函数曲线,见图1、图2。

Figure 1. Parameter alpha frequency distribution histogram and posterior distribution density function curve
图1. 参数α频率分布直方图和后验分布密度函数曲线
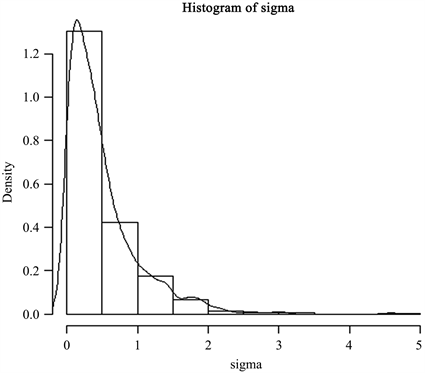
Figure 2. Parameter sigma frequency distribution histogram and posterior distribution density function curve
图2. 参数σ频率分布直方图和后验分布密度函数曲线
最终通过图1、图2取得 、 的后验均值作为参数估计值,并得到 、 的近似贝叶斯估计值,见表1。
Table 1. Parameter estimate of AR(2) model
表1. AR(2)模型的参数估计值结果
通过表1可以得知,近似贝叶斯方法、最小二乘法得出的参数估计值都与真实值接近,具有较好的估计效果。虽然近似贝叶斯方法与最小二乘法的参数估计效果相当,但近似贝叶斯方法可以得到参数的“近似后验分布”,从而可以估计参数的其余性质。
4. 实例分析
本文选用1998年1月到2016年12月国际布伦特原油期货月度收盘价格数据,共228个。用RStudio软件画出数据的时序图,由图3可看出数据是不平稳序列,故对数据先取对数,再进行一阶差分处理,得到原油期货月度收盘价格对数增量序列的时序图,见图4。
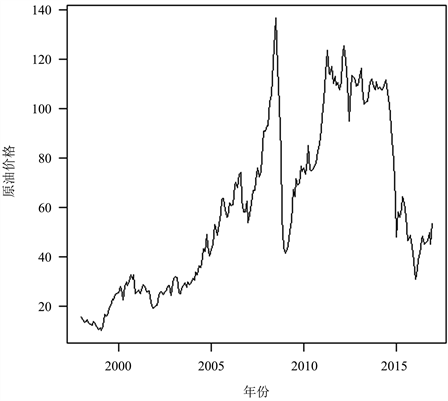
Figure 3. Crude oil futures closing price series
图3. 原油期货收盘价序列
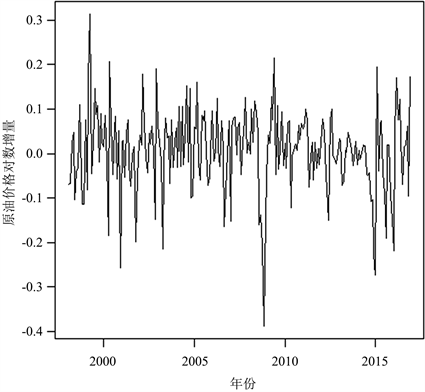
Figure 4. Crude oil futures closing price’s logarithm increment series
图4. 原油期货收盘价对数增量序列
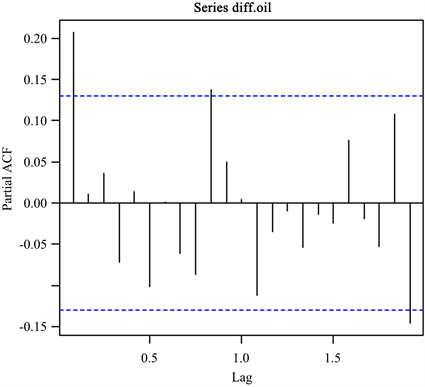
Figure 5. PACF diagram
图5. PACF图
可以发现图4数据分布大致平稳,故对其进行单位根检验得知增量序列不存在单位根,所以原油期货月度收盘价格增量序列为平稳时间序列。通过偏相关函数(PACF图),见图5,初步认为适合该数据的模型为AR(1)模型。从图3、图4中可以看出,受2008年金融危机影响,数据在2008年时有较大波动,存在异常值,使用最小二乘法去估计参数可能存在误差;所以我们可以运用近似贝叶斯算法去估计这个模型的参数,得到参数 , 的频率分布直方图和后验分布密度函数曲线,见图6,图7。
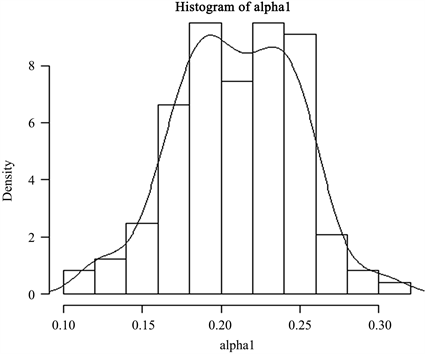
Figure 6. Parameter alpha1 frequency distribution histogram and posterior distribution density function curve
图6. α1的频率分布直方图与后验分布密度函数曲线

Figure 7. Parameter sigma frequency distribution histogram and posterior distribution density function curve
图7. σ的频率分布直方图与后验分布密度函数曲线
最终通过图6,图7取得 , 的后验均值作为参数估计值,见表2。
Table 2. Parameter estimate
表2. 参数估计值
5. 总结
本文基于近似贝叶斯方法和最小二乘法这两种方法,对AR(p)模型参数估计问题进行分析研究,并针对AR(2)模型,应用本文中两类方法对参数估计的效果进行模拟及验证分析。通过数据模拟实验,发现这两种方法都能得到相应的模型参数的值,且模拟得到的参数值与真实值很接近;通过实例分析得知,近似贝叶斯方法对参数估计应用范围更广,能够在数据存在异常值等复杂的情况下使用。针对AR(p)模型参数估计方法进行研究时,以下问题值得在未来作进一步的思考和研究:能否把近似贝叶斯方法应用到更加复杂的时间序列模型中,如ARMA模型。
文章引用
陈博文,夏 莉. 基于近似贝叶斯方法的AR(p)模型参数估计问题研究
Research on Parameter Estimation of AR(p) Model Based on Approximate Bayesian Computation[J]. 应用数学进展, 2021, 10(03): 680-688. https://doi.org/10.12677/AAM.2021.103074
参考文献
- 1. 王玉丽, 包为民, 沈丹丹, 等. AR模型参数的抗差递推估计[J]. 中国农村水利水电, 2017(6): 74-77.
- 2. 王志坚. 稳健AR模型的构建及其在金融时序中的应用[J]. 统计与信息论坛, 2017, 32(5): 57-63.
- 3. 王志坚, 王斌会. 稳健AR模型的构建及比较研究[J]. 数学的实践与认识, 2019(13): 156-166.
- 4. 朱慧明, 韩玉启, 郑进城. 基于正态Gamma共轭先验分布的贝叶斯AR(p)预测模型[J]. 统计与决策, 2005(2): 10-11.
- 5. 章敏, 李再兴. AR(1)模型中参数估计的偏差分析[J]. 统计与决策, 2016(6): 26-28.
- 6. 彭毳鑫, 胡敏, 赵志文. 条件矩约束下一阶自回归模型的参数经验似然推断[J]. 统计与决策, 2018, 34(21): 33-37.
- 7. 陈阳, 夏志明, 高海菊. AR(p)模型参数估计和定阶的Lasso方法[J]. 西北大学学报: 自然科学网络版, 2011, 9(6): 483.
- 8. 谢琍, 唐甜, 王晓瑞. 线性空间自回归模型的不同惩罚函数下参数估计的比较及其实证分析[J]. 数理统计与管理, 2019(5): 823-835.
- 9. Rubin, D.B. (1984) Bayesianly Justifiable and Relevant Frequency Calculations for the Applies Statistician. Annals of Statistics, 12, 1151-1172. https://doi.org/10.1214/aos/1176346785
- 10. 钱瑾. 基于合成似然的近似贝叶斯方法[D]: [硕士学位论文]. 上海: 华东理工大学, 2017.
- 11. 张晨. 基于近似贝叶斯计算的参数估计和模型选择的研究[D]: [硕士学位论文]. 合肥: 合肥工业大学, 2019.
- 12. 张岚, 钱夕元. 基于近似贝叶斯计算方法的排队模型参数估计[J]. 上海理工大学学报, 2020, 42(2): 108-114.
- 13. 黄鹂. 近似贝叶斯方法及其应用研究[D]: [硕士学位论文]. 苏州: 苏州大学, 2018.
- 14. 周双酉. 基于HMC的合成似然近似贝叶斯及其应用[D]: [硕士学位论文]. 上海: 华东理工大学, 2019.
- 15. 王振龙, 胡永宏. 应用时间序列分析[M]. 北京: 科学出版社, 2007: 98-99.
- 16. 陈杨林, 刘业. AR(p)模型参数估计方法比较和实证分析[J]. 南昌大学学报(理科版), 2014(38): 127.
- 17. Pritchard, J.K., Seielstad, M.T., Perez-Lezaun, A., et al. (1999) Population Growth of Human Y Chromosomes: A Study of Y Chromosome Microsatellites. Molecular Biology & Evolution, 16, 1791-1798. https://doi.org/10.1093/oxfordjournals.molbev.a026091
