Modeling and Simulation
Vol.
12
No.
06
(
2023
), Article ID:
75790
,
12
pages
10.12677/MOS.2023.126496
不同信息下N-策略休假排队系统中 患者均衡行为分析
唐婧,陈燕婷*
上海理工大学,管理学院,上海
收稿日期:2023年9月27日;录用日期:2023年11月15日;发布日期:2023年11月22日

摘要
患者到医院诊疗时,某些体检项目需要用到大型机器进行检查,若机器一直处于开机状态则会持续发热、加快损耗和长时间辐射,甚至可能发生故障。为解决此问题,本文主要考虑了带有N-策略和双阶段休假策略的M/M/1排队模型。本文采用“收益–成本”结构来量化患者的等待时间成本和服务后收益,由于患者往往是追求最大化自己的收益来决定去留,从而患者与患者之间出现了博弈现象。假设患者在到达时可以通过获取系统信息来做出进队或止步的决策,当受到不同信息水平影响时,患者会出现不同的思考与选择。通过构造马尔可夫状态转移方程,研究在完全可见和几乎不可见两种情形下系统的稳态分布和患者进队的均衡策略。最后本文将用一些数值例子说明,在不同信息水平下,主要参数变化对患者均衡进队概率的影响。
关键词
休假排队,N-策略,排队博弈,不同信息水平,均衡策略

Analysis of Patients’ Equilibrium Behavior in N-Strategy Vacation Queueing Systems under Different Information
Jing Tang, Yanting Chen*
Business School, University of Shanghai for Science and Technology, Shanghai
Received: Sep. 27th, 2023; accepted: Nov. 15th, 2023; published: Nov. 22nd, 2023

ABSTRACT
When patients come to the hospital for diagnosis and treatment, certain physical examination items require the use of large machines for examination. If the machine is constantly turned on, it will continue to heat, accelerate loss, and cause long-term radiation, and may even malfunction. To address this issue, this article mainly considers a M/M/1 queueing model with N-strategy and two-stage vacation strategy. Here, the “benefit-cost” structure is used to quantify the waiting time cost and post service benefits of patients. As patients often seek to maximize their own benefits to decide whether to stay or not, there is a game phenomenon between them. Assuming that patients can make decisions to enter or stop by obtaining system information upon arrival, when influenced by different levels of information, patients have different thoughts and choices. By constructing a Markov state transition equation, we will study the steady-state distribution of the system and the equilibrium strategy for patient admission in both fully visible and almost invisible situations. Finally, some numerical examples are used to illustrate the impact of changes in main parameters on the balanced admission probability of patients at different levels of information.
Keywords:Vacation Queueing, N-Strategy, Queueing Game, Different Levels of Information, Equilibrium Strategy

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言与文献综述
目前越来越多的人群主动关心自己的身体健康,入职体检、企业团检、日常体检也越来越普遍。某些体检项目需要用到大型机器设备进行检查,若机器一直处于开机状态则会持续发热、加快损耗和长时间辐射,甚至可能发生故障。依据服务台在服务过程中发生故障而不能为顾客服务等不可靠行为的实际情况,人们在排队基础上引入了休假机制。自1975年Levy [1] 提出休假模型之后,休假排队模型因其广泛适用性而受到诸多学者研究。国内学者田乃硕 [2] 对休假排队的现状和方法包括各种休假规则模型的描述、稳态指标等进行了简要介绍。2002年,Servi和Finn [3] 首次提出了一种半休假策略,即工作休假,也就是服务台在服务过程中以比正常工作时较低的速率进行工作。这表示在工作休假期间,系统仍能提供服务,同时也可以从事一部分其他工作进行缓冲。2015年,Ye和Liu [4] 把休假和工作休假两种休假策略结合起来,引入了一种双休假策略排队模型,发现能有效的降低计算机网络的能源消耗。当前刘煜飞 [5] 在此基础上进行了拓展,研究了具有双阶段休假模式驱动的流体模型。
高乾 [6] 在研究中提到商场自动扶梯的工作原理,通过对比研究发现,在这种模式下,能一定程度上降低机器和能源的损耗。但是与自动扶梯相比,医院大型机器从休假到正常工作状态的切换往往需要一定的时间和费用,因此如果系统中仅出现了一个或少数几个患者而又频繁进行切换时,从经济性上看是不可行的。由此提出了N-策略。Yadin [7] 最早将N-策略引入排队系统,接着Kella [8] 将其拓展到M/G/1排队系统中,并考虑了收益成本的经济行为。所谓N-策略,具体是指直到系统中至少出现N个患者进行排队时,才开始启动机器进入正常工作状态。基于工厂订单装配系统的运行机制,王勋和徐秀丽 [9] 将N-策略和休假模式进行了结合。但是该模型在医院等其他现实场景下需要考虑更多,因为患者具有流动性,会根据系统状态或者自身情况等选择是否加入系统。马庆庆 [10] 在文中也提到患者到达系统时获取信息的能力并不相同,年轻人可以通过网上预约判断排队人数,但是老年人一般通过线下取号,获取信息的能力较弱。由于患者往往是通过最大化自己的收益来决定去留,从而患者与患者之间出现了博弈现象。本文采用Naor [11] 提出的“收益–成本”结构,通过量化患者的等待时间成本和服务后收益,从而得到患者均衡策略和社会最优策略。如高珊和王金亭 [12] 使用此理论,分析了带Bernoulli休假的不可见M/M/1重试排队模型的进队策略。
综上所述,已有学者将N策略、双阶段休假排队和信息是否可见两两进行结合研究 [13] [14] ,但目前还未有研究将它们三者一起应用于现实场景中。为解决现实中医疗设备耗能问题,提高社会整体效益,本文将两种策略进行联合,建立N策略下双阶段休假排队模型。并且基于该机制,探讨在信息完全可见和信息几乎不可见两种情形下,患者的均衡进队策略。
2. 模型与分析
假设在一个无限等待空间的单服务台排队系统中,正常工作速率服从参数为μ的指数分布,患者到达服从参数为λ的泊松过程,且遵循先到先服务(FCFS)的规则。为保证系统稳定,设 。令 表示系统在t时刻的状态,其中N(t)表示t时刻的患者数, 表示t时刻服务台的状态:0为工作休假状态,1为休假状态,2为正常工作状态。系统 是一个连续时间的二维随机马尔可夫过程。当队列为空时,系统先进入工作休假状态,以一个比正常工作时较低的速率η进行服务。当一个工作休假期结束后,系统非空,则系统转为正常工作状态。若系统仍然为空,将进入休假状态,此时不提供任何服务。但患者可以到达系统中继续排队,直至系统队列中至少有N个患者等待时,系统才开始启动进入正常工作状态。工作休假时间与休假时间分别服从参数为θw和θv的指数分布。上述排队系统可以简化为以下流程图1:

Figure 1. Queueing system operation flowchart
图1. 排队系统运行流程图
假设患者在到达时可以获取系统信息,来决定是进队还是止步,并且一旦他们做出决定便不能中途退出系统或是止步后重新进入系统。患者在博弈的过程中,会依据当前的系统信息来预估服务收益及所需花费的等待成本,以便做出对自己最有利的选择。假设在完成服务后,每位患者将获得R单位的收益,他们在系统中单位等待时间成本为常数C。 和 分别表示当患者到达时,系统中的人数为n,系统状态为i (i = 0, 1, 2),并且选择进入排队后在系统中的平均逗留时间和获得的收益。通过收支结构可知: 。当 时,患者的服务收益大于其等待时间成本,只要患者选择进队就能获得正收益。当 时,患者的服务收益等于其等待时间成本,进队与否对于患者来说没有区别。当 时,患者不会加入系统,从而出现止步现象。
3. 不同信息下排队系统中患者的均衡策略
3.1. 信息完全可见情形
在信息完全可见情形下,患者到达时既能够知晓系统中的总人数也知道此时服务台所处于的状态。因为在系统中总人数达到一定值时,后到达的患者会因为等待时间的增加而获得负收益,意味着这些患者不会进入系统。假定当患者到达时发现系统处于工作休假状态(状态0),且队长超过阈值Nw时,他们就不会进入系统。同样当患者到达时发现系统处于正常工作状态(状态2),且队长超过阈值Nv时,他们也不会进入系统。即存在止步策略(Nw, 0)和(Nv, 2)。在工作休假期间,服务速率明显小于正常工作时的速率,当患者知晓服务台的状态处于工作休假时,相对更容易止步,显然有 。此时系统状态转移图如下图2所示:
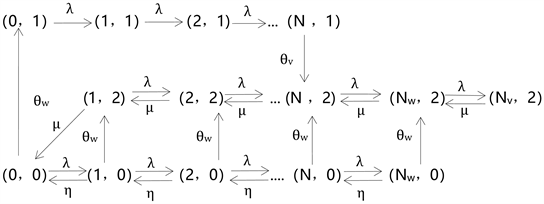
Figure 2. System state transition diagram with fully visible information
图2. 信息完全可见下系统状态转移图
在这种情形下, 表示当患者到达时,系统中等待人数为n,系统状态为i (i = 0, 1, 2),并且选择进入排队后在系统中的平均逗留时间。根据均值分析法,一步转移概率有:
, (1)
, (2)
, (3)
, (4)
, (5)
对(1)式关于n求导得: ,因为 ,则 。那么 关于n是单调递减的, 最大值为 。由此可以知道,当系统处于休假状态时,后到达患者花费的总时间反而更少。当系统处于工作休假时,易得当系统中人数越多,后到达患者等待的时间越长。由(3)式可得: 。为考虑实际情况,患者在队列空闲时,一定会加入系统,也就是其预期收益为正值,即完成服务后的收益大于由于等待所带来的时间成本。因此在本文模型中均有如下假设: ,且 。若发现系统处于休假状态,他们进队则会获得正收益,所以在休假阶段不存在止步阈值。
通过反复迭代(3)式并结合(4)式和(5)式可以推出:
, (6)
定义
为标记患者看到系统中患者数为k并且服务台处于状态i (i = 0, 1, 2)时的收益。休假状态下,当
时,即
。此时通过计算无法直接求出关于k精确的数学表达式,这里采取图解法(详见4.1节),可以解得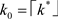 。正常工作状态下,当
时,直接计算得出
。正常工作状态下,当
时,直接计算得出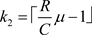 。所以存在止步阈值
。所以存在止步阈值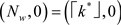 和
和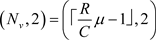 。
。
3.2. 信息几乎不可见情形
在信息几乎不可见情形下,患者到达时能够知晓服务台此时所处于的状态但不知道系统中的总人数。假设他们加入系统的概率为qi (i为此时服务台所处于的状态,i = 0, 1, 2)。令 , , ,则系统的状态转移图如图3所示:
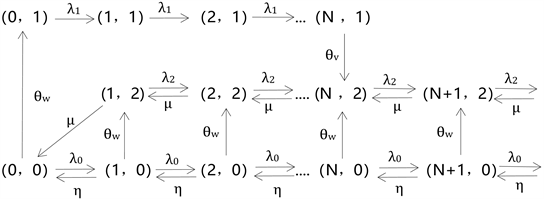
Figure 3. System state transition diagram with almost invisible information
图3. 信息几乎不可见下系统状态转移图
在该情形下, 表示系统中总人数为n,系统状态为i (i = 0, 1, 2)时的稳态概率。根据上图可以列出该系统的平衡方程:
, (7)
, (8)
, (9)
, (10)
, (11)
, (12)
, (13)
, (14)
将公式(8)转化为
, (15)
由于公式(15)是一个二阶齐次常系数线性差分方程,可写出其对应的特征方程为:
(16)
解方程可得,它有两个解分别为:
,
由Elaydi [15] 差分方程理论可知,对任意的 ,可以设 ,其中,d1,d2为待定系数。由于 表示的是概率,而 ,所以d1一定为0,设
, (17)
将式(17)代入式(14)中,则有:
(18)
由式(18)变化得:
, (19)
将式(19)进行反复迭代可以得到:
, (20)
由式(7)和式(17)求出 和 ,并代入式(20)可得:
,
其中: , 。
通过以上计算求出:
, (21)
当n=N时,由式(13)和式(21)可得:
(22)
根据归一化条件: 求得:
求出常数d2后,根据上述表达式,可以分别得到系统中各个节点的稳态概率。因为由已知条件 可知,当患者到达发现服务台处于休假状态时,只要选择加入系统,他将一定获得正的平均收益。所以,他的最优策略为选择进队,即 , ,这也是唯一的纳什均衡策略。下面可以继续讨论当患者到达时发现服务台处于工作休假状态时的两种情形。当 时,此时 , 。
情形1:当 时,存在唯一的均衡策略:
, 。
证明:
在几乎不可见情形下带N-策略的双阶段休假模型中,标记一个患者,当他到达系统时,服务台状态为工作休假时,若该患者此时选择入队,可以求出他的平均逗留时间为:
该标记患者的平均收益为: 。
当 时,此时 。在这种情形下,如果患者抵达时已知当前服务台处于工作休假阶段,若全部以概率1加入系统,那么当标记患者到达并选择进入系统后,他将获得非正的平均收益。所以 不是此种情形下的均衡策略。同样可知 也非均衡策略。因此,有且仅有概率 ,使得患者无论是否进队都没有影响。 ,因为 ,可以观察得到x2是关于q0的函数,而且利用函数求导有:
, 。
因此x2关于q0是单调递增的。但 关于q0是单调递减的,当 时得临解:
然后利用式(10)中 ,求出对应的解:
情形2:
当 时,存在唯一的纳什均衡策略 。
这种情况下,无论其他患者采用何种进队策略,该标记患者只要选择加入系统,他将必然获得正的平均收益。所以,他的最优决策就是选择进队,即 。并且这也是唯一的纳什均衡策略。
4. 数值分析
本节将针对上文中提到的模型展开数值分析,研究在信息完全可见与信息几乎不可见两种情形下,不同参数变化对患者均衡进队策略的影响。并且本节还将利用Matlab软件,分别对各参数的灵敏性进行分析。
4.1. 信息完全可见下止步阈值数的变化分析
在第3.1节中通过计算无法直接求出k精确的数学表达式,这里采用图解法,在同一坐标系上绘制
和
。方程的解将是两条曲线交点横坐标的值,可以解得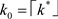 。
。
① 当 时,得到患者的止步阈值,如图4所示:
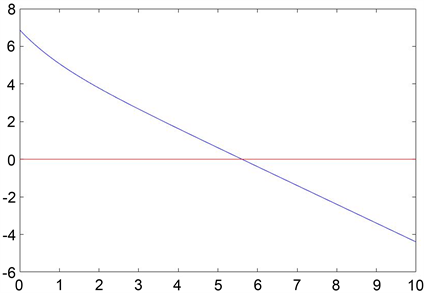
Figure 4. Work leave stop threshold chart
图4. 工作休假止步阈值图
由图4可知在这种情况下,k* = 6,即当系统处于工作休假时,系统中排队人数超过6人时,后进队患者的等待时间成本一定大于其获得的收益,止步将是其最优的选择。下面将讨论在这种情况下,参数θw和η的变化,对患者止步阈值数的影响。
② 当 时,其他参数不变,只改变η的值(取值范围为0.1~0.9),观察止步阈值k的变化,如图5所示:
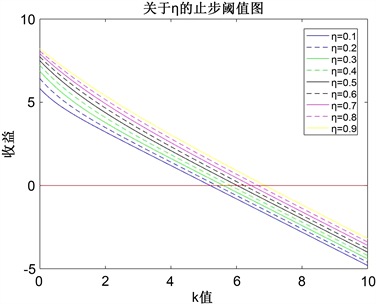
Figure 5. The impact of parameter η on the number of stopping thresholds
图5. 参数η对止步阈值数的影响图
由图5可知,其他参数不变,参数η与k值呈现正相关变化规律。这是因为η代表的是系统在工作休假期间的服务速率,服务速率越快,后进入患者所需的等待时间相应越少,也就更倾向于进入系统。但从总体上可以发现参数η的变化对k值影响并不明显。
③ 当 时,其他参数不变,只改变θw的值(取值范围为0.1~0.9),观察止步阈值k的变化,如图6所示:

Figure 6. The impact of parameter θw on the number of stopping thresholds
图6. 参数θw对止步阈值数的影响图
由上图6可知,其他参数不变,改变θw的值可以发现,θw减小时,k值减小,θw增大时k值也相应增大。这是因为θw的倒数值代表工作休假时间,且正常工作速率明显大于工作休假时的服务速率,当工作休假时间越短,患者进入排队后被服务的等待时间也越短,意味着患者更愿意进入系统。其次,相比于上文参数η的变化,可以发现参数θw的变化对k值变化的影响更加明显,这可能与患者的不耐烦等待情绪有关。
4.2. 信息几乎不可见下患者均衡策略分析
在信息几乎不可见的情形下,探讨工作休假期间患者的均衡策略随不同参数的变化关系。由上文3.2节中已知如下关系式:
, ,接下
来分别研究参数λ,μ,θw和η的变化对患者均衡进队概率 的影响。
④ 当 时,患者均衡进队概率随参数λ的变化如图7所示。
⑤ 当 时,患者均衡进队概率随参数μ的变化如图8所示。
⑥ 当 时,患者均衡进队概率随参数η的变化如图9所示。
⑦ 当 时,患者均衡进队概率随参数θw的变化如图10所示。
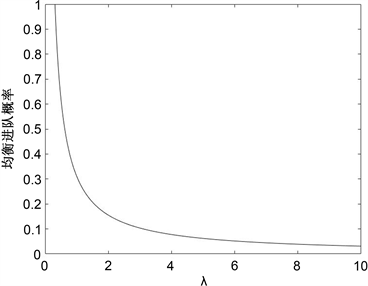
Figure 7. The impact of parameter λ on the balanced admission probability of patients
图7. 参数λ对患者均衡进队概率的影响
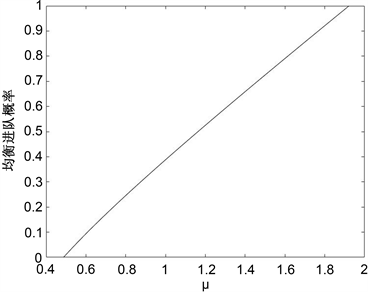
Figure 8. The impact of parameter μ on the balanced admission probability of patients
图8. 参数μ对患者均衡进队概率的影响

Figure 9. The impact of parameter η on the balanced admission probability of patients
图9. 参数η对患者均衡进队概率的影响
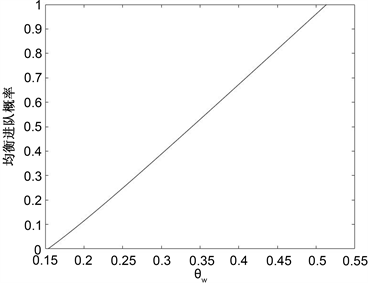
Figure 10. The impact of parameter θw on the balanced admission probability of patients
图10. 参数θw对患者均衡进队概率的影响
由图7可以看出在信息几乎不可见情形下,患者均衡进队概率随着λ的增大而逐渐减小。这是因为患者对系统信息掌握不完全时,逐步上升的到达速率会导致系统负荷的增大,因此在这种情况下患者会偏向于止步。图8和图9都表明患者均衡进队概率随着工作速率的提高而上升,这是由于服务台不管处于何种阶段,提高相应的服务速率,都有助于减少患者的预期等待时间,进而增强他们加入系统的意愿。由图10可以发现,在系统中,当工作休假时间增加时,顾客进队的概率会逐渐降低。这是因为工作休假服务速率明显低于正常工作,工作休假时间是指工作休假状态向正常工作状态转化时间的,当转化时间过长时,由于患者的不耐烦情绪等会影响他们入队。为提升患者的进队概率,可以考虑适当提升服务台的服务速率和缩短工作休假的时间,从而提升患者的满意度。
5. 结论与建议
本文从医院大型机器能源损耗问题出发,建立了带N-策略的双阶段休假排队模型。在情形一信息完全可见下,分别探讨了参数η和θw对患者止步阈值数的影响。从整体上看,相比于参数η的变化,可以发现参数θw的变化对其止步阈值数变化的影响更加明显。在情形二信息部分可见情形下,当系统为工作休假状态时,探讨各个参数变化对患者均衡进队概率的影响,并且对数值结果进行了分析说明。
综上所述,为提升患者的进队概率,降低患者的止步门槛,可以考虑适当提升服务台的服务速率和缩短工作休假的时间。并且可以发现与提高工作休假的服务速率相比,缩短工作休假时间,可能达到更好的效果。在今后的研究中可以探讨造成此类现象发生的可能因素,并且还可以拓展到信息几乎可见和信息完全不可见的情形。
基金项目
本研究由上海理工大学管理学院2021年度科研启动项目(KYQD202101)资助。
文章引用
唐 婧,陈燕婷. 不同信息下N-策略休假排队系统中患者均衡行为分析
Analysis of Patients’ Equilibrium Behavior in N-Strategy Vacation Queueing Systems under Different Information[J]. 建模与仿真, 2023, 12(06): 5464-5475. https://doi.org/10.12677/MOS.2023.126496
参考文献
- 1. Levy, Y. and Yechiali, U. (1975) Utilization of Idle Time in an M/G/1 Queueing System. Management Science, 22, 202-211. https://doi.org/10.1287/mnsc.22.2.202
- 2. 田乃硕. 休假随机服务系统[J]. 运筹学杂志, 1990(1): 17-30+70.
- 3. Servi, L.D. and Finn, S.G. (2002) M/M/1 Queues with Working Vacations (M/M/1/WV). Performance Evalu-ation, 50, 41-52. https://doi.org/10.1016/S0166-5316(02)00057-3
- 4. Ye, Q. and Liu, L. (2015) The Analysis of the M/M/1 Queue with Two Vacation Policies. International Journal of Computer Mathematics, 94, 115-134. https://doi.org/10.1080/00207160.2015.1091450
- 5. 刘煜飞, 叶晴晴. 基于矩阵分析方法的具有双阶段休假的排队系统驱动的流模型性能分析[J]. 数学的实践与认识, 2021, 51(4): 189-199.
- 6. 高乾. 自动扶梯设备节能技术及节能调度系统分析[J]. 中国电梯, 2022, 33(9): 10-13.
- 7. Naor, P. and Yadin, M. (1963) Queuing Systems with a Removable SERVICE Station. Journal of the Operational Research Society, 14, 393-405. https://doi.org/10.1057/jors.1963.63
- 8. Kella, O. (1989) Thethreshold Policy in the M/G/1 Queue with Server Vaca-tions. Naval Research Logistics, 36, 111-123. https://doi.org/10.1002/1520-6750(198902)36:1<111::AID-NAV3220360109>3.0.CO;2-3
- 9. 王勋, 徐秀丽. 带N策略的双阶段休假M/M/1排队系统驱动的流体模型性能分析[J/OL]. 运筹学学报: 1-11. http://kns.cnki.net/kcms/detail/31.1732.O1.20220424.1746.052.html, 2023-11-15.
- 10. 马庆庆, 刘维奇, 李继红. N-策略休假排队系统中异质信息患者策略分析[J]. 运筹与管理, 2021, 30(11): 40-46.
- 11. Naor, P. (1969) The Regulation of Queue Size by Levying Tolls. Econometrica, 37, 15-24. https://doi.org/10.2307/1909200
- 12. 高珊, 王金亭. 具有Bernoulli休假的不可见M/M/1重试排队模型的进队策略分析[J]. 应用数学学报, 2017, 40(1): 106-120.
- 13. 陈莹, 叶晴晴, 武彧睿. 不完全信息下具有双阶段休假模式的排队系统均衡策略研究[J]. 数学的实践与认识, 2021, 51(8): 178-191.
- 14. 张博, 李凯. 不可观察的N-策略工作休假M/M/1/Q排队系统分析[J]. 合肥工业大学学报(自然科学版), 2021, 44(12): 1710-1715.
- 15. Elaydi, S.N. (2005) An In-troduction to Difference Equations. Springer, New York.
NOTES
*通讯作者。