Advances in Applied Mathematics
Vol.
11
No.
11
(
2022
), Article ID:
58458
,
10
pages
10.12677/AAM.2022.1111861
带有工作休假的可见M/M/2排队系统均衡 策略研究
苏思琦,叶晴晴
南京信息工程大学数学与统计学院,江苏 南京
收稿日期:2022年10月23日;录用日期:2022年11月18日;发布日期:2022年11月28日

摘要
本文研究了带有工作休假的可见M/M/2排队系统的均衡止步策略和社会最优策略。在带有工作休假的M/M/2排队中,两个服务台独立工作,并且在休假期间以较低的服务速率进行工作,而不是完全停止工作。顾客到达排队系统后,根据对队长和服务台状态的观察,并结合收支结构,决定是否进入排队或止步。基于带有工作休假的M/M/2排队系统,本文研究了完全可见情形下的顾客均衡止步策略,并且从社会收益的角度分析了顾客的纳什均衡策略,得到了所有顾客遵循相同均衡阈值策略下的社会最优策略。最后,通过数值例子说明了系统参数对社会收益的影响,得到社会收益关于排队系统在正常忙期与工作休假期间服务时间和休假时间呈负相关的结论。
关键词
M/M/2排队,止步,均衡策略,纳什均衡,工作休假

Research on Equilibrium Strategies of Observable M/M/2 Queue with Working Vacations
Siqi Su, Qingqing Ye
School of Mathematics and Statistics, Nanjing University of Information Science and Technology, Nanjing Jiangsu
Received: Oct. 23rd, 2022; accepted: Nov. 18th, 2022; published: Nov. 28th, 2022

ABSTRACT
The equilibrium balking strategies and social optimal strategies are investigated in the paper for observable M/M/2 queue with working vacations. In such an M/M/2 queue with working vacations, two servers work independently and work with a lower service rate rather than stopping work altogether during the vacation period. Upon customers arrive at the queuing system, they decide whether to join or balk the queue based on observation of the queue length and the status of the servers, along with the reward-cost structure of the system. Based on the M/M/2 queue with working vacations, we study customers’ equilibrium joining strategies in the fully observable case. We analyse customers’ equilibrium strategies in terms of the social welfare, and obtain the social optimal strategies under which all customers follow the same equilibrium threshold strategies. Finally, a numerical example is given to illustrate the influence of system parameters on social welfare. It is found that the social welfare is negatively related to the service time during normal busy period and working vacation period and vacation time.
Keywords:M/M/2 Queue, Balking, Equilibrium Strategies, Nash Equilibrium, Working Vacations

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在过去的几十年中,人们致力于研究可见排队系统,该系统涉及顾客的个体行为和社会最优控制。Naor [1] 率先提出对可见的单服务台排队系统进行经济分析,即到达的顾客可观察到队长,然后决定是否进队。Edelson和Hildebrand [2] 考虑了不可见的情形,即顾客在不知道排队状态的情况下做出决定。Hassin和Haviv [3] 进行了具有优先级的排队模型的经济分析,其中可以购买两个优先级,并且得到了所有纳什均衡策略(纯阈值策略)。与经典排队系统不同,顾客可以根据其到达得到的可用信息做出自己的决定。因此,这些系统可以被建模为顾客之间的博弈,而基本问题是确定纳什均衡。到目前为止,越来越多的文献涉及对M/M/1排队的顾客止步行为的经济分析,具体参见 [4] - [12] 等。Hassin,Haviv [13] 和Stidham [14] 的专著总结了关于各种可见模型的主要方法和几个结果,并提供了大量参考文献。
大量文献考虑了经典休假排队模型中顾客的策略行为。Burnetas和Economou [5] 最先研究了具有启动时间的M/M/1休假排队系统,并且分别得到了可见情形和不可见情形下的顾客均衡阈值策略。Sun等 [11] 在Burnetas和Economou [5] 的模型基础上,研究了具有启动和关闭的可见M/M/1休假排队系统中的均衡阈值策略。Economou等 [15] 研究得到了休假时间和服务时间是服从一般分布的不可见M/G/1排队系统中的顾客纳什均衡和社会最优进队策略。Guo和Hassin [10] 研究了N-策略休假的M/M/1排队系统,并且分别得到了完全可见和完全不可见情形下顾客均衡止步策略和社会最优策略。Guo和Li [16] 分析了N-策略休假M/M/1的排队系统,得到了几乎可见情形下顾客的策略行为。Liu等 [17] 研究了具有单重休假的离散和连续可见排队系统中顾客的均衡阈值策略。Ma等 [18] 研究了具有多重休假的Geo/Geo/1排队系统中顾客的均衡止步策略。Wang等 [19] 应用博弈论研究了具有同步和异步多重休假的M/M/K排队系统,并得到了顾客的均衡止步策略和社会收益函数。在他们具有多重休假的M/M/K排队模型中,服务台在休假期间完全停止服务,而在实际生活中经常会碰到服务台在休假期间也会为顾客做辅助工作的情形,例如,当处于下班时间或节假日期间,医院的线上咨询系统会为患者提供在线服务。于是,本文对Wang等 [19] 的模型进行了推广,研究了一个工作休假的M/M/K排队系统,该系统允许服务台在休假期间以较低的速率为顾客提供服务。
本文研究了带有工作休假的M/M/2排队中顾客的均衡行为。系统中的两个服务台独立工作,并且在工作休假期间以较低地速率工作,而不是完全停止工作。本文将根据到达时可观察到的信息,研究顾客进队或止步的最佳策略,即当顾客到达时,已知队长和服务台状态下对顾客的纳什均衡进行研究。并且,本文研究了当所有顾客遵循相同均衡阈值策略情况下的社会收益。最后,通过数值例子说明系统参数对社会收益的影响。
本文研究了具有工作休假的可见M/M/2排队系统的顾客均衡止步策略和社会最优策略,在此模型中,两个服务台独立地在工作和休假这两个状态间交替,并在对应状态下提供相应的服务。本文所研究的排队模型具有一定的应用价值,可应用于具有并行子系统的在线咨询服务系统的建模,例如线上医院咨询服务系统。对于这样的线上咨询服务系统,子系统可能会独立地进入休假期,即当一个子系统处于以较低速率提供服务的工作休假期时,另一个子系统可能会以正常速率提供服务,其研究理论可以为系统决策者提供相应的决策建议。
本文剩余部分的结构如下:第2节中具体描述了带有工作休假的M/M/2排队模型和收支结构;第3节中确定了完全可见排队的顾客均衡止步策略;第4节中计算了系统的稳态概率分布,并得到了社会最优策略;在第5节中,通过数值实验,分析系统参数对社会收益的影响。
2. 模型描述
本文考虑一个具有无限等待空间的两服务台排队系统,顾客到达是参数为 的泊松过程,服务顺序是先到先服务。每个服务台独立地有两种服务状态:正常忙期和工作休假期。一旦服务台前没有顾客,它就开始进入平均持续时间为 的工作休假期。如果在工作休假期间有顾客到达,则服务台以比较低的速率 提供服务。如果工作休假期结束时服务台前依然没有顾客到达,服务台进入下一个工作休假期,直到服务台前有顾客。否则,它将立即切换成正常工作状态为顾客提供服务。当处于正常忙期时,每个服务台的服务速率为 ,此外,假设两个服务台独立地在正常忙期和工作休假期间交替,两种服务状态下的服务时间和休假时间都服从指数分布,并且 。
用 表示t时刻系统的状态,其中 和 分别表示系统中的顾客数和处于正常忙期的服务台数量,则随机过程 是一个连续马尔可夫链,状态空间为 ,并且非零转移率为
对应的状态转移图如图1所示。
顾客在到达时根据系统中顾客数量和服务台状态来选择进入排队和止步的行为是本文需要研究的行为策略。为了对决策过程建模,本文假设每个顾客在被服务后可以获得R单位的收益,这反映的是顾客的对服务的满意程度或者被服务的附加价值。另一方面,每个顾客在系统中(排队或服务中)单位时间的等但成本为C。顾客都是风险中立的并且使他们的平均收益最大化。当到达系统后,顾客通过自己掌握的系统顾客数量和服务台状态这两个信息,评估出自身的平均等待收益,并依此做出进队或止步的决定。规定顾客在做出选择后不能反悔,既不能在排队中途退出也不能在止步后重新到达。
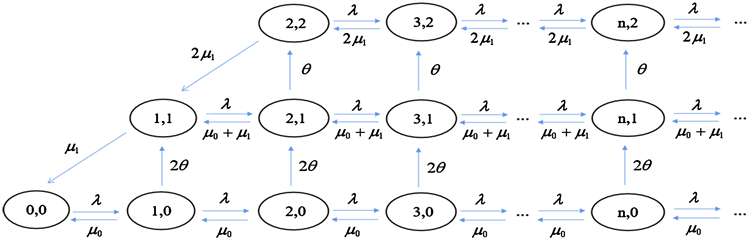
Figure 1. Transition rate diagram of the working vacations queue model
图1. 工作休假排队模型的状态转移图
下面,本文将对带有工作休假策略的排队模型展开经济学分析,得到完全可见情形下顾客的均衡止步策略和所有顾客遵循相同均衡阈值策略情况下的社会最优策略。并且通过对工作休假排队模型中性能指标的参数效应分析,实现对工作休假模型更优化的设计和控制,提高实际系统的运行效率,在实际应用中获得更大的经济效益。
3. 完全可见情形的均衡止步策略
本节研究了两个服务台独立的在正常忙期和工作休假期之间交替的可见排队,通过收支结构和分析出的顾客平均逗留时间来求解顾客的均衡止步策略。完全可见情形下,顾客在到达系统时,可以观察到服务台的状态 和系统中的顾客数 ,并遵循纯阈值进队策略 ,即顾客在t时刻到达系统,观察到系统状态为 ,如果 ,他们就选择进入排队,如果 ,他们就选择止步。
定理1. 在完全可见的M/M/2工作休假排队中,存在均衡的阈值进队策略 ,并且该策略是个弱占优的策略。
(1)
(2)
(3)
其中, 是方程
(4)
的唯一解; 是方程
(5)
的唯一解。
证明 由收支结构可知,一个新到达的顾客到达发现系统状态为 ,他选择进入排队的平均收益是
(6)
其中 表示该顾客选择进队后在系统中的平均逗留时间。通过对一步状态转移率的分析,有以下方程:
(7)
(8)
(9)
(10)
(11)
将(11)代入(10)得到非齐次常系数一阶差分方程:
(12)
根据初始条件(9),求解得到(12)的特解:
(13)
将(13)代入(8)得到非齐次常系数一阶差分方程:
(14)
根据初始条件(7),求解得到(14)的特解:
(15)
很容易检验 , 和 关于n是单调递增的。当完成服务后获得的收益大于等于逗留成本,即 ,顾客是愿意选择进入排队;当完成服务后获得的收益小于逗留成本,即 ,顾客就会选择止步。利用(6),(11),(13)和(15)解不等式 ,可以得到结论,当且仅当 时,顾客会选择进入排队,当 时,顾客会选择止步,其中 如(1),(2)和(3)所示。
在工作休假的M/M/2排队模型里,假设
(16)
这确保了顾客到达发现系统为空时选择进入后的平均收益大于0,否则顾客在系统为空时到达将永远不会进入排队。注意到,在该策略下顾客的行为不会受到其他顾客行为的影响,即这是一个弱占优的策略。综上,定理1得证。
4. 完全可见情形的社会最优策略
在本节中继续研究带有工作休假的可见M/M/2排队系统,并且从社会收益的角度分析了顾客的均衡止步策略。基于矩阵几何法,求得排队系统的稳态概率分布,从而得到社会最优策略。在完全可见情形下,当顾客遵循均衡阈值策略 时,带有工作故障的M/M/2排队模型的状态转移图见图2。
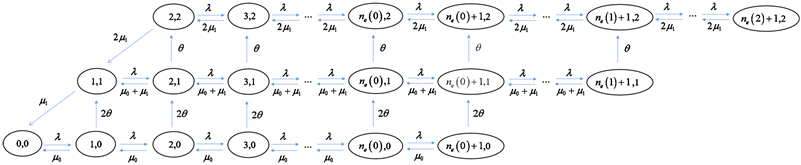
Figure 2. Transition rate diagram of the fully observable queue with working vacations
图2. 完全可见情形下带有工作休假排队的状态转移图
按照字典顺序排列,该连续时间马尔可夫过程 的无穷小生成元可表示为
 (17)
(17)
其中
由Q矩阵的结构可以看出连续时间马尔可夫链 是拟生灭过程,那么这一随机过程的极限概率存在,即随机过程 达到平稳状态,定义排队系统中的顾客数与服务台正常忙期数量的稳态联合概率分布为
(18)
引入稳态概率向量 ,其中 和 为一维行向量, 和 为二维行向量, 为三维行向量。对Q矩阵的左不变向量求逆后,得到系统的稳态概率分布。
根据Hassin和Haviv [13] 对社会收益的定义,本文将社会收益定义为所有进入系统顾客的总收益,即社会收益是选择进队顾客的平均收益之和。 为所有顾客均遵循均衡阈值策略 时单位时间的社会收益。则它可以表示为
(19)
5. 数值例子
本节通过数值实验分析了在带有工作休假的可见M/M/2的排队系统中系统参数对社会收益的影响。本文主要研究了服务台在正常忙期的服务速率对社会收益的影响,服务台在工作休假期间的服务速率对社会收益的影响,以及服务台休假时间对社会收益的影响。具体结果如下:
如图3,当 ,,,, 时,随着 的变化,系统社会收益 的变化趋势,由图可知, 随着 的增加而增加,即社会收益随着系统在正常忙期内的服务速率增加而增加。从实际情况来看,正常忙期内的服务速率越大,顾客的平均逗留时间越短,他们更乐意进入排队,从而社会收益会有增加的趋势。
如图4,当 ,,,, 时,随着 的变化,系统社会收益 的变化趋势,由图可知, 随着 的增加而增加,即系统在工作休假期内的服务速率增加,社会收益也随之增加。
如图5,当 ,,,, 时,随着 的变化,系统社会收益 的变化趋势,由图可知, 随着 的增加而增加,即社会收益随着系统休假时间的减小而增加。从实际情况来看,服务台的休假时间越长,顾客更不愿意进入排队,社会收益会减少。

Figure 3. versus
图3. 随 的变化曲线
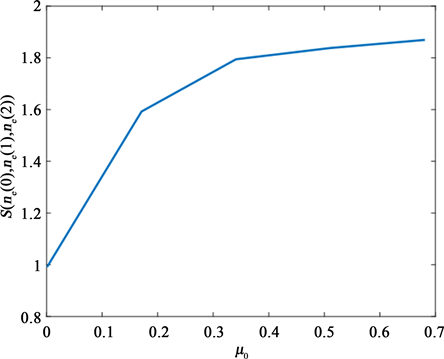
Figure 4. versus
图4. 随 的变化曲线
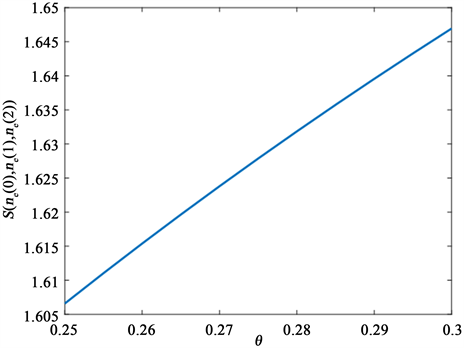
Figure 5. versus
图5. 随 的变化曲线
6. 结论
本文研究了带有工作休假的可见M/M/2排队系统中的顾客均衡止步策略和社会收益,并给出了数值例子来说明系统参数对社会收益的影响。
本文首先分析出完全可见情形下顾客的平均逗留时间,通过收支结构,得出顾客的均衡止步策略。其次,基于矩阵几何法求出系统的稳态概率分布,从而得到社会最优策略。最后通过数值例子说明服务台在正常忙期和工作休假期间的服务速率和休假时间对社会收益的影响,从实验结果来看,社会收益与服务台正常忙期和工作休假的服务时间以及休假时间是呈负相关的。排队系统在正常忙期内的服务速率越大,顾客更乐意进入排队,从而社会收益会增加;系统在工作休假期内的服务速率增加,社会收益也会随之增加;服务台的休假时间越长,顾客更不愿意进入排队,社会收益会减少。
基金项目
国家自然科学基金青年项目(11901307)。
文章引用
苏思琦,叶晴晴. 带有工作休假的可见M/M/2排队系统均衡策略研究
Research on Equilibrium Strategies of Observable M/M/2 Queue with Working Vacations[J]. 应用数学进展, 2022, 11(11): 8128-8137. https://doi.org/10.12677/AAM.2022.1111861
参考文献
- 1. Naor, P. (1969) The Regulation of Queue Size by Levying Tolls. Econometrica, 37, 15-24. https://doi.org/10.2307/1909200
- 2. Edelson, N.M. and Hildebrand, K. (1975) Congestion Tolls for Poisson Queueing Processes. Econometrica, 43, 81-92. https://doi.org/10.2307/1913415
- 3. Hassin, R. and Haviv, M. (1997) Equilibrium Threshold Strategies: The Case of Queues with Priorities. Operational Research, 45, 966-973. https://doi.org/10.1287/opre.45.6.966
- 4. Boudali, O. and Economou, A. (2012) Optimal and Equilibrium Balking Strategies in the Single Server Markovian Queue with Catastrophes. European Journal of Operational Research, 218, 708-715. https://doi.org/10.1016/j.ejor.2011.11.043
- 5. Burnetas, A. and Economou, A. (2007) Equilibrium Customer Strategies in a Single Server Markovian Queue with Setup Times. Queueing Systems, 56, 213-228. https://doi.org/10.1007/s11134-007-9036-7
- 6. Economou, A. and Kanta, S. (2008) On Balking Strategies and Pricing for the Single Server Markovian Queue with Compartmented Waiting Space. Queueing Systems, 59, 237-269. https://doi.org/10.1007/s11134-008-9083-8
- 7. Economou, A. and Kanta, S. (2008) Equilibrium Balking Strate-gies in the Observable Single-Server Queue with Breakdowns and Repairs. Operations Research Letters, 36, 696-699. https://doi.org/10.1016/j.orl.2008.06.006
- 8. Economou, A. and Kanta, S. (2011) Equilibrium Customer Strategies and Social-Profit Maximization in the Single- Server Constant Retrial Queue. Naval Research Logistics, 58, 107-122. https://doi.org/10.1002/nav.20444
- 9. Economou, A. and Manou, A. (2012) Equilibrium Balking Strategies for a Clearing Queueing Systems in Alternating Environment. Annals of Operations Research, 208, 489-514. https://doi.org/10.1007/s10479-011-1025-x
- 10. Guo, P. and Hassin, R. (2011) Strategic Behavior and Social Op-timization in Markovian Vacation Queues. Operational Research, 59, 986-997. https://doi.org/10.1287/opre.1100.0907
- 11. Sun, W., Guo, P. and Tian, N. (2010) Equilibrium Threshold Strate-gies in Observable Queueing Systems with Setup/Closedown Times. Central European Journal of Operations Research, 18, 241-268. https://doi.org/10.1007/s10100-009-0104-4
- 12. Wang, J. and Zhang, F. (2011) Equilibrium Analysis of the Ob-servable Queues with Balking and Delayed Repairs. Applied Mathematics and Computation, 218, 2716-2729. https://doi.org/10.1016/j.amc.2011.08.012
- 13. Hassin, R. and Haviv, M. (2003) To Queue or Not to Queue: Equilibrium Behavior in Queueing Systems. Kluwer Academic Publishers, Boston. https://doi.org/10.1007/978-1-4615-0359-0
- 14. Stidham Jr., S. (2009) Optimal Design of Queueing Systems. CRC Press, Taylor and Francis, Boca Raton. https://doi.org/10.1201/9781420010008
- 15. Economou, A., Gomez-Corral, A. and Kanta, S. (2011) Optimal Balking Strategies in Single-Server Queues with General Service and Vacation Times. Performance Evaluation, 68, 967-982. https://doi.org/10.1016/j.peva.2011.07.001
- 16. Guo, P. and Li, Q. (2013) Strategic Behavior and Social Optimization in Partially-Observable Markovian Vacation Queues. Operations Research Letters, 41, 277-284. https://doi.org/10.1016/j.orl.2013.02.005
- 17. Liu, W., Ma, Y. and Li, J. (2012) Equilibrium Threshold Strategies in Observable Queueing Systems under Single Vacation Policy. Applied Mathematical Modelling, 36, 6186-6202. https://doi.org/10.1016/j.apm.2012.02.003
- 18. Ma, Y., Liu, W. and Li, J. (2013) Equilibrium Balking Behavior in the Geo/Geo/1 Queueing Systems with Multiple Vacations. Applied Mathematical Modelling, 37, 3861-3878. https://doi.org/10.1016/j.apm.2012.08.017
- 19. Wang, J., Zhang, Y. and Zhang, Z.G. (2021) Strategic Joining in an M/M/K Queue with Asynchronous and Synchronous Multiple Vacations. The Journal of the Operational Research Society, 1, 161-179. https://doi.org/10.1080/01605682.2019.1644978