Pure Mathematics
Vol.
08
No.
06
(
2018
), Article ID:
27512
,
7
pages
10.12677/PM.2018.86085
Global Attractor for a Class of Nonlinear Generalized Kirchhoff Equation
Penghui Lv*, Xiaojun Lv
School of information, Tourism and Cultural College, Yunnan University, Lijiang Yunnan
Received: Oct. 17th, 2018; accepted: Oct. 29th, 2018; published: Nov. 13th, 2018

ABSTRACT
The paper studies the longtime behavior of solutions to the initial boundary value problem (IBVP) for a class of Kirchhoff models: . We show the semigroup has a -global attractor.
Keywords:Generalized Kirchhoff Equation, Well-Posedness, Global Attractor

一类广义非线性Kirchhoff型方程的整体吸引子
吕鹏辉*,吕小俊
云南大学旅游文化学院信息学院,云南 丽江
收稿日期:2018年10月17日;录用日期:2018年10月29日;发布日期:2018年11月13日

摘 要
该文研究了广义Kirchhoff型方程: 的初边值问题的解的长时间行为。证明上述问题对应的算子半群 存在 -整体吸引子。
关键词 :广义Kirchhoff方程,适定性,整体吸引子

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文研究下列非线性Kirchhoff型方程的整体吸引子:
, (1.1)
, (1.2)
. (1.3)
其中
是 中具有光滑边界的有界域,
,且
都是正常数,有关
的假设将会在后文中给出。
中具有光滑边界的有界域,
,且
都是正常数,有关
的假设将会在后文中给出。
整体吸引子是学习各种耗散非线性演化方程解的渐近性行为的基本概念。从物理学观念看,耗散方程(1.1)的整体吸引子表示在自然能量空间中从任何时间点开始最终都将处于永久状态,其维数表示相关湍流现象的自由度的数量,因此表示流动性的复杂程度。关于吸引子和其维数的所有信息都将定性性质限定为定量性质,从而产生关于该物理系统可以产生的有关流体的有价值的信息 [1] [2] [3] [4] 。
关于Kirchhoff方程已经有了很多深入的研究。Igor Chueshov [5] 研究了下列具有非线性强阻尼的Kirchhoff波方程的长时间行为:
. (1.4)
近年,Cheng Jian ling和Yang Zhijian [6] 研究了下列具有强阻尼项的Kirchhoff型方程的长时间行为:
, (1.7)
其中 , 。 是具有光滑边界 的有界域。
Yang Zhijian [7] 也研究了在 中具有强阻尼想的Kirchhoff型方程的长时间行为:
, (1.8)
其中 , 。 是具有光滑边界 的有界域, 是一个外力项。文章证明了有关连续解半群 拥有整体吸引子,同时存在有限分形维数和Hausdorff维数。
Meihua Yang和Chunyou Sun [8] 研究了在非线性临界增长条件下,强阻尼波方程的整体吸引子的存在性:
, (1.9)
该整体吸引子为在
中有界,且在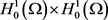 范数下吸引
中的每个有界集。
范数下吸引
中的每个有界集。
Vittotino和Sergey Zelik [9] 证明了下列半线性强阻尼波方程紧整体吸引子:
. (1.10)
Penghui Lv,Jingxin Lu和Guoguang Lin [10] 证明了下列广义非线性Kirchhoff方程的整体吸引子:
. (1.11)
该文得到了半群 在空间 中存在整体吸引子。
关于波方程的整体吸引子,多数集中研究其 -整体吸引子,同样的,文献 [10] 中得到 -整体吸引子,为了更进一步研究(1.11)的长时间性态,现在关心的问题是对(1.11)是否存在一个紧的 -整体吸引子。通过研究,结论是肯定的。
2. 记号和主要结论
为叙述方便,我们引入下列符号:
其中 。 为 的共轭空间, 。 是L2-内积下的Sobolev空间,同时 表示 在 中的闭包( )。符号 表示H-内积。
定义算子 ,
则,算子 是正定的且空间 是Hilbert空间
,
特别的,
.
定理2.1 [10] :假定
(H1) , , ,
(H2) ,
(H3) , 。则问题(1.1)~(1.3)的唯一解 满足
,
其中 在 中为非减函数。
评论2.1 [10] :在定理2.1的条件下,可以得到 及 是有界函数。
定理2.2 [10] :在定理2.1的条件下,则由方程(1.1)的解在能量空间
下的连续半群
在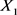 中存在整体吸引子
。
中存在整体吸引子
。
定理2.3:在定理2.1的条件下,则由方程(1.1)的解在能量空间 下的连续半群 在 中渐近光滑的。
3. -整体吸引子A
引理3.1:在假设(H1)~(H3)条件下,所有的 ,我们有下列不等式
,
其中 在 中为非减函数。
证明:定义
.
则根据评论2.1及定理2.1易得:
, (3.1)
(1.1)与 作H内积得到
. (3.2)
由
, (3.3)
及
. (3.4)
利用定理2.1,我们得到
. (3.5)
首先对
,(3.5)乘以 ,并对
求
积分,得到
,并对
求
积分,得到
.
结合定理2.1及(3.1),我们最终得到不等式
. (3.6)
当 时,(3.5)对 求 积分,得到
. (3.7)
结合(3.1)、(3.6)及(3.7),我们最终得到不等式
. (3.8)
结合(3.6)及(3.8),结论得证。
引理3.2:在假设(H1)~(H3)条件下,所有的 ,我们有下列不等式
,
其中 在 中为非减函数。
证明:设 ,则方程(1.1)化为
. (3.9)
定义
.
(3.9)与 作H内积得到
.
由
(3.10)
及
. (3.11)
利用定理2.1,我们得到
. (3.12)
首先对 ,(3.12)乘以 ,并对 求 积分,由定理2.1得到
.
即有
. (3.13)
当
时,(3.12)对
求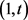 积分,得到
积分,得到
. (3.14)
结合(3.13)及(3.14),结论得证。
在引理3.1和引理3.2下可以得到, 在 有界。
下面,我们将证明 为 -整体吸引子。为得到结果,由引理3.1和引理3.2 (引理说明有界 -吸收集存在 ),我们仅需证明渐近紧性。
引理3.3:(在V-范数下的连续性) 令 在X1-范数下的收敛序列,则对任意的 , 在X2-范数下为收敛序列。
证明:令 为初值 得到的相关解,令 ,则z满足
. (3.15)
初值条件为
.
边界条件为
.
(3.15)与 作H内积得到
,
其中
,
及
.
由此,我们得到
.
结合 在X1-范数下的连续性及 的任意性,得到 在X2-范数下,在 中连续。
引理3.4:在假设(H1)~(H3)条件下, 为 -渐近紧。
证明:由引理3.1和引理3.2及定理2.1及引理3.3,我们即可得到 在有界 -吸收集从X1到X2是Lipschitz的,即说明其 -渐近紧。
结合以上结论,我们得到下面定理:
定理3.2:((X1, X2)-整体吸引子的存在性) 在假设(H1)~(H3)条件下, 为方程(1.1)的解在能量空间X1下的连续半群,则 有 -整体吸引子A,其中,A在X2中是紧的、不变的,同时,在X2范数下吸引X1中的每个有界子集。
文章引用
吕鹏辉,吕小俊. 一类广义非线性Kirchhoff型方程的整体吸引子
Global Attractor for a Class of Nonlinear Generalized Kirchhoff Equation[J]. 理论数学, 2018, 08(06): 637-643. https://doi.org/10.12677/PM.2018.86085
参考文献
- 1. Yang, Z.J., Feng, N. and Ma, T.F. (2015) Global Attractor for the Generalized Double Dispersion Equation. Nonlinear Analysis, 115, 103-116.
https://doi.org/10.1016/j.na.2014.12.006 - 2. 杨志坚, 程建玲. Kirchhoff型方程解的渐近行为[J]. 数学物理学报, 2011, 31A(4): 1008-1021.
- 3. Pata, V. and Zelik, S. (2006) Smooth Attractors for Strongly Damped Wave Equations. Nonlinearity, 19, 1495-1506.
https://doi.org/10.1088/0951-7715/19/7/001 - 4. Lin, G.G. (2011) Nonlinear Evolution Equation. Yunnan University Press, Kunming.
- 5. Chueshov, I. (2012) Long-Time Dynamics of Kirchhoff Wave Models with Strong Nonlinear Damping. Journal of Differential Equations, 252, 1229-1262.
https://doi.org/10.1016/j.jde.2011.08.022 - 6. Cheng, J.L. and Yang, Z.J. (2011) As-ymptotic Behavior of the Kirchhoff Type Equation. Acta Mathematica Scientia, 31A, 1008-1021.
- 7. Yang, Z.J. (2007) Longtime Behavior of the Kirchhoff Type Equation with Strong Damping on RN. Journal of Differential Equations, 242, 269-286.
https://doi.org/10.1016/j.jde.2007.08.004 - 8. Yang, M.H. and Sun, C.Y. (2009) Attractors for Strongly Damped Wave Equa-tions. Nonlinear Analysis, 10, 1097-1100.
https://doi.org/10.1016/j.nonrwa.2007.12.001 - 9. Pata, V. and Squassina. M. (2005) On the Strongly Damped Wave Equation. Communications in Mathematical Physics, 253, 511-533.
https://doi.org/10.1007/s00220-004-1233-1 - 10. Lv, P.H., Lu, J.X. and Lin, G.G. (2016) Global Attractor for a Class of Non-linear Generalized Kirchhoff Models. Journal of Advances in Mathematics, 12, 6452-6462.