Pure Mathematics
Vol.
09
No.
06
(
2019
), Article ID:
31731
,
11
pages
10.12677/PM.2019.96095
Dynamic Analysis of a Phytoplankton-Zooplankton Ecological Model with Tax Measures
Huideng Li
Wenzhou University, Wenzhou Zhejiang

Received: Jul. 20th, 2019; accepted: Jul. 30th, 2019; published: Aug. 16th, 2019

ABSTRACT
This passage studies a phytoplankton-zooplankton ecological model with tax measure, and discusses the existence and local asymptotic stability of the equilibrium point. According to the Routh-Hurwitz Criterion, the critical conditions for the local asymptotic stability of the equilibrium point are investigated. Using Pontryagin Maximum Principle, the optimal equilibrium solution is obtained to achieve the optimal tax revenue, which can get the tax revenue value to maximize the discount value of social income. Numerical simulation works verify the feasibility and effectiveness of the theoretical results, and analyze the impact mechanism of tax measure on the dynamics of the model. Finally, these results can provide a theoretical basis for resource managers to formulate resource management policies rationally.
Keywords:Phytoplankton, Zooplankton, Tax Measure, Equilibrium, Stability
一类具有税收措施的浮游植物–浮游动物生态 模型的动力学分析
李辉登
温州大学,浙江 温州

收稿日期:2019年7月20日;录用日期:2019年7月30日;发布日期:2019年8月16日

摘 要
本文研究了一类具有税收措施的浮游植物–浮游动物生态模型,探讨了模型平衡点的存在性和局部渐近稳定性,利用Routh-Hurwitz判据得到了平衡点局部渐近稳定的临界条件,依据Pontryagin极大值原理求解出达到最优税收的最优平衡解,得到使社会收入贴现值为最大的税收值。数值模拟工作验证了理论结果的可行性与有效性,并分析了税收措施对模型动力学性态的影响机制。这些研究结果给资源管理者合理制定资源管理政策提供了理论依据。
关键词 :浮游植物,浮游动物,税收措施,平衡点,稳定性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,浮游生物(plankton)是指悬浮在水体中的生物,是水生食物链的最要组成部分,在水生生态系统中占有重要地位,可划分为浮游植物和浮游动物两大类 [1] [2] 。浮游植物(phytoplankton)是指在水中以浮游生活的微小植物,通常是指浮游藻类,他们是初级生产者,是水生态系统食物链的基础,且是浮游动物的食物来源。
随着社会经济快速发展和社会人口的迅速繁衍,人类对自然资源的巨大需求和大规模的开采行为已导致基础资源出现削弱、退化、枯竭现象,与此同时也带来严重的环境污染问题,直接威胁到人类和其它生物的生存与发展。近几十年来,大量学者研究了浮游植物–浮游动物生态模型 [3] [4] [5] [6] [7] ,获得一些比较优秀的成果。Chattopadhyay [3] 等人研究了有毒浮游植物和浮游动物生态模型,探讨了产毒浮游植物在浮游生物种群生长动态过程中的影响作用。Roy [4] 在单一营养条件下构建了浮游植物生态模型,研究了无毒和有毒浮游植物之间的相互作用机制。Sata T和Bandyopadhyay [5] 考虑了浮游植物毒素释放具有离散时间变化特征,构建了带有离散时间变化特征的浮游植物–浮游动物生态模型,研究了毒素释放离散时间变化特征对浮游植物和浮游动物生长动态变化趋势的影响作用。文献 [6] 构建了一类营养盐–浮游生物生态模型,研究了有毒物质如何抑制浮游植物和浮游动物的生长速率。Mukhopadhyay [7] 在浮游植物水华背景下,构建了一类水体富营养化生态模型,研究了营养盐与浮游植物之间的交互作用。
然而目前,税收捕获如何影响浮游植物与浮游动物之间交互作用的研究相对较少。针对资源可持续问题,Clark [8] [9] 和Mesterton-Gibbons [10] [11] 等人构建了几类具有最优收获策略的捕食–食饵生态模型,探讨了如何实施收获策略才能维持渔业的可持续发展。Pahari和Kar [12] 等人考虑到政府一般采取多种方式进行监管,通常会考虑税收、产权租赁、季节性捕获和直接管制等措施,构建了一类可替代食饵的捕食–食饵生态模型,探讨如何选择性地对捕食者进行捕获,进而维持渔业的可持续发展。霍 [13] 等人构建了一个具有保护区和税收的渔业资源动态模型,研究了保护区和税收对渔业资源可持续发展的影响作用。Kar、Dubey、Chaudhui等学者 [14] [15] [16] [17] 利用税收作为控制变量构建渔业资源动态模型,他们也探讨了如何通过税收措施维持渔业资源的可持续发展。
2. 生态建模
基于Sata T和Bandyopadhyay [5] 和Bandyopadhyay [3] 等人提出的有毒浮游植物–浮游动物生态模型:
(1)
P是产毒浮游植物在t时刻的密度,Z是浮游动物在t时刻的密度。r表示浮游植物的内禀生长率,k表示浮游植物在水环境中的最大环境承载量, 表示浮游动物的捕获率, 表示Holling 功能反应项的半饱和系数, 表示生物量转化率(满足限制条件 ),d表示捕食者种群的死亡率,参数 表示每单位生物量浮游植物产生毒性物质的速率。假设浮游植物对浮游动物生长的贡献与有毒物质对浮游动物死亡的贡献成正比,因此,可用 表示有毒物质导致浮游动物死亡情况。同时,假设 ,即浮游动物转化量高于有毒物质导致浮游动物的死亡量。
依据上述假设,对模型(1)进行修改,有选择性地进行比例捕获。同时,引入税收变量,通过调节税收来防止渔民过渡捕获,从而使渔业资源可持续发展,进而建立如下模型来揭示比例捕获和税收措施如何影响浮游植物与浮游动物的动态变化趋势。
(2)
其中假设只对浮游动物进行捕获, 表示捕获者所获得种群资源的净经济收入。q为可捕获系数,E表示对浮游动物种群的捕获强度, 表示在捕获强度存在的条件下所获得的资源量,这与捕获强度E有关。 表示单位资源Z的市场价格,管理者对单位资源的税收为 ,若 ,表示管理者对资源进行保护,管理者要对捕获者所捕获的资源进行税收,若 ,表示管理者对捕获者进行补偿。通常情况下,我们假设 ,c表示Z的捕获成本, 表示税收对捕获的影响成正比。关于
的具体解释参考文献 [17] 。同时假设 ,当 时,有 。由生物
学意义可知所有参数均取正数,即仅在区域 内对模型(2)进行理论与数值讨论。
引理1:对所有的 ,模型(2)所有的解 和 在初始条件下都是正的。
证明 将模型(2)改写为
(3)
其中 , , 。
方程(3)在满足初始条件下,可得到 ,同理,得到 , 。
显然,模型(2)的所有解都是正的。
引理2:对所有的 ,模型(2)中所有的解 和 在初始条件下都是一致有界的。
证明 设函数 , 关于t求导联立(2)有
(4)
对任意的 ,有
(5)
取 ,得到
(6)
其中 。则有
(7)
当 时,可以得到 。
因此当 时,对任意的 ,模型(2)的所有解都定义在区域
(8)
3. 平衡点存在性与稳定性
通过计算模型(2)存在四个平衡点 , , , ,平衡点 显然永远存在,下面主要考虑 , 存在的充分性条件。
定理1 若满足条件 ,则平衡点 是存在的。
证明 平衡点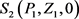 满足如下方程:
满足如下方程:
 (9)
(9)
解得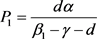 ,
, 。
。
所以由条件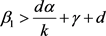 得
得 都大于0。定理证毕。
都大于0。定理证毕。
定理2 若条件
 ,
,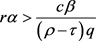 (10)
(10)
和 (11)
(11)
满足,则平衡点 是唯一存在的。
是唯一存在的。
证明 平衡点 满足方程:
满足方程:
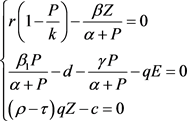 (12)
(12)
解得
 ,
,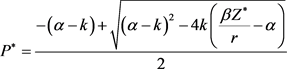 ,
,
由 ,
, ,可知
,可知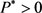 ,
, 。当
。当 时,可知
时,可知 ,故
,故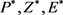 都
都
大于0。
同时模型(2)的Jacobian矩阵为
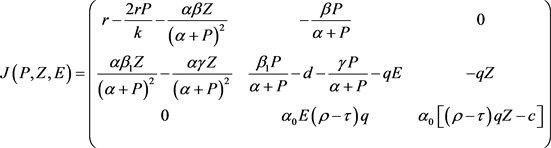 (13)
(13)
1) 平衡点 对应的特征根分别为
对应的特征根分别为 ,
,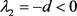 ,
,
因此 是一个鞍点。
是一个鞍点。
2) 平衡点 的特征方程为
的特征方程为 ,易知,所有的特征根均小于0,因此平衡点
,易知,所有的特征根均小于0,因此平衡点 是局部渐近稳定的。
是局部渐近稳定的。
定理3 如果满足 和
和 ,则平衡点
,则平衡点 是局部渐近稳定的。
是局部渐近稳定的。
证明 模型(2)在平衡点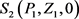 的特征方程为
的特征方程为
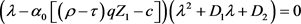 (14)
(14)
其中 ,
, 。
。
当 和
和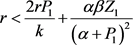 成立时,其特征值均为负,因此
成立时,其特征值均为负,因此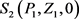 是局部渐近稳定的。
是局部渐近稳定的。
模型(2)在平衡点 处的Jacobian为
处的Jacobian为
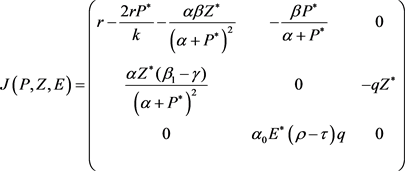 (15)
(15)
其特征方程为:
 (16)
(16)
其中
 (17)
(17)
 (18)
(18)
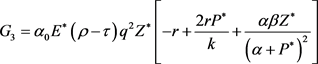 (19)
(19)
当 时,可知
时,可知


即 ,由Routh-Hurwitz判别法可知方程(16)的根均有负实部,正平衡点
,由Routh-Hurwitz判别法可知方程(16)的根均有负实部,正平衡点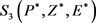 是局部渐近稳定的。于是有以下定理:
是局部渐近稳定的。于是有以下定理:
定理4 当 时,正平衡点
时,正平衡点 是局部渐近稳定的。
是局部渐近稳定的。
4. 最优税收策略
在实际问题中,最优税收政策就是通过调节税收即使得人类在捕获活动中的总收入达到最大值,又能保证自然资源持续发展,这个目标社会收入的贴现值可表示为:
 (20)
(20)
其中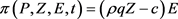 ,
, 为年贴现率,解决这个最优问题,就是确定一个税收策略
为年贴现率,解决这个最优问题,就是确定一个税收策略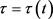 使得J在满足状态方程(2)和控制约束条件
使得J在满足状态方程(2)和控制约束条件 下取得最大值。
下取得最大值。
现构造控制问题的Hamiltion函数:
 (21)
(21)
其中 都是伴随变量 [8] ,假设Hamiltion函数不会在
都是伴随变量 [8] ,假设Hamiltion函数不会在 或者
或者 取得最大值,从而可得奇异控制 [8]
取得最大值,从而可得奇异控制 [8]
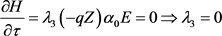 (22)
(22)
根据Pontryagin最大值原理有
 (23)
(23)
 (24)
(24)
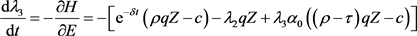 (25)
(25)
由(25)得
 (26)
(26)
把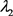 的结果代入(23)得到
的结果代入(23)得到
 (27)
(27)
其中
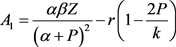 ,
,
上述微分方程的解为
 (28)
(28)
其中 是一个常数。当
是一个常数。当 ,
, 时,影子价格
时,影子价格 是有界的。
是有界的。
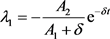 (29)
(29)
同理,由(24)和(29)可得
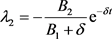 (30)
(30)
其中
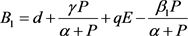 ,
, 
由(26)和(30)联立有
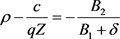 (31)
(31)
把正平衡点 代入(31)式得到一个关于
代入(31)式得到一个关于 的方程,此方程的解(如果存在的话)用
的方程,此方程的解(如果存在的话)用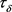 表示,再将
表示,再将
 代入
代入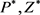 和
和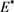 ,可得最优平衡解(
,可得最优平衡解(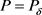 ,
,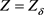 ,
, )和最优税收
)和最优税收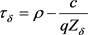 。
。
现在建立了最优平衡解的存在条件,满足了最大原理的必要条件,因此正如Clark指出,由Bang-Bang控制和非平衡奇异控制组合而成的最优路径是很难找到的,因此,我们只考虑一个最优平衡。
注:从本节进行的上述分析,我们观察以下情况:
i) 从(22),(29)和(30),注意到 ,(
,( 是伴随变量)在最优平衡的时间间隔内保持恒定。因此,当
是伴随变量)在最优平衡的时间间隔内保持恒定。因此,当 时,它们满足在
时,它们满足在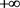 上的横截性条件。
上的横截性条件。
ii) 考虑到内平衡点,(25)式可以改写成
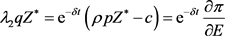
这意味着单位收获的总用户成本等于稳定状态水平下未来价格的折扣值。
iii) 在(31)式中,当 时,
时,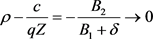 。因此,净收益
。因此,净收益 ,这意味着
,这意味着
当贴现率是无限时,净收益趋于0。
5. 数值模拟
现在主要通过数据仿真来验证理论结果的有效性和可行性,且进一步探讨税收措施如何影响模型(2)的动力学性态,其参数取值为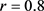 ,
, ,
, ,
, ,
, ,
,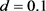 ,
, ,
, ,
, ,
, ,
, ,
, 。依据定理2和定理4,可计算平衡点为
。依据定理2和定理4,可计算平衡点为 ,且是局部渐近稳定的,详细见图1和图2,进而说明所得理论结果是可行的。
,且是局部渐近稳定的,详细见图1和图2,进而说明所得理论结果是可行的。
依据理论推导可知税收措施可以对捕获起到一定的控制作用,从而影响浮游植物和浮游动物的种群密度动态变化趋势。从图3~图5不难看出,渔民所获得的收益随着税收的增加而减少,同时渔民就会减少对浮游动物的捕获(即捕获强度减低),因此浮游动物种群密度就会增加,从而导致浮游植物种群密度逐渐减少,因而,税收措施严重影响浮游植物和浮游动物的种群密度动态变化趋势。

Figure 1. Phase space trajectories when 
图1. 当 时的相位图
时的相位图
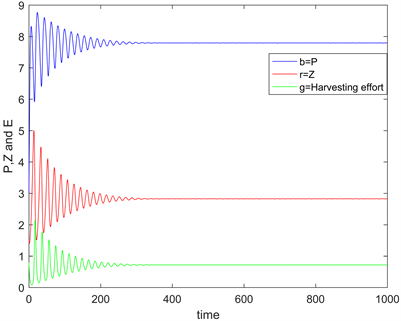
Figure 2. Time series when 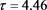
图2. 当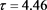 时的时间序列图
时的时间序列图

Figure 3. Dynamic trends of phytoplankton for different tax levels
图3. 不同税收水平下的浮游植物的动态变化趋势

Figure 4. Dynamic trends of zooplankton for different tax levels
图4. 不同税收水平下的浮游动物的动态变化趋势

Figure 5. Dynamic trends of harvesting intensity for different tax levels
图5. 不同税收水平下收获强度的动态变化趋势
6. 结论
本文构建了具有税收措施的产毒浮游植物–浮游动物生态模型,讨论了模型的正性、有界性和平衡点的存在性;利用Routh-Hurwitz判据,得到了平衡点局部渐近稳定的临界条件;依据Pontryagin最大值原理探讨了税收措施的最优平衡解,得到了使社会收入贴现值为最大的税收值。数值模拟验证了理论结果的可行性与有效性。总而言之,这些研究结果为资源管理者合理制定资源管理政策提供了理论依据。
文章引用
李辉登. 一类具有税收措施的浮游植物–浮游动物生态模型的动力学分析
Dynamic Analysis of a Phytoplankton-Zooplankton Ecological Model with Tax Measures[J]. 理论数学, 2019, 09(06): 712-722. https://doi.org/10.12677/PM.2019.96095
参考文献
- 1. El Abdllaoui, A., Chattopadhyay, J. and Arino, O. (2002) Comparisons by Models of Some Basic Mechanisms Acting on the Dynamics of the Zooplankton-Toxic Phytoplankton System. Mathematical Models and Methods in Applied Sciences, 12, 1421-1451.
https://doi.org/10.1142/S0218202502002185 - 2. Nørgaard, E. (1959) Fundamentals of Ecology. Oikos, 10, 290-291.
https://doi.org/10.2307/3565152 - 3. Chattopadhayay, J., Sarkar, R.R. and Mandal, S. (2002) Toxin-Producing Plankton May Act as a Biological Control for Planktonic Blooms—Field Study and Mathematical Modelling. Journal of Theoretical Biology, 215, 333-344.
- 4. Roy, S. (2009) The Coevolution of Two Phytoplankton Species on a Single Resource: Allelopathy as a Pseudo-Mixotrophy. Theoretical Population Biology, 75, 68-75.
- 5. Saha, T. and Bandyopadhyay, M. (2009) Dynamical Analysis of Toxin Producing Phytoplank-ton—Zooplankton Interactions. Nonlinear Analysis Real World Applications, 10, 314-332.
https://doi.org/10.1016/j.nonrwa.2007.09.001 - 6. Jang, R.J., Baglama, J. and Rick, J. (2006) Nutri-ent-Phytoplankton-Zooplankton Models with a Toxin. Mathematical and Computer Modelling, 43, 105-118.
https://doi.org/10.1016/j.mcm.2005.09.030 - 7. Mukhopadhyay, B. and Bhattacharyya, R. (2006) Modelling Phytoplankton Allelopathy in a Nutrient-Plankton Model with Spatial Heterogeneity. Ecological Modelling, 198, 163-173.
https://doi.org/10.1016/j.ecolmodel.2006.04.005 - 8. Clark, C.W. (1976) Mathematical Bioeconomic: The Optimal Management of Renewable Resources. Biometrics, 49, 674.
https://doi.org/10.2307/2532591 - 9. Clark, C.W. (1989) Bioeconomic Modeling and Resource Management. In: Levin, S.A., Hallam, T.G. and Gross, L.J., Eds., Applied Mathematical Ecology. Biomathematics, Springer, Berlin, Heidelberg, 11-57.
https://doi.org/10.1007/978-3-642-61317-3_2 - 10. Mesterton-Gibbons, M. (1988) On the Optimal Policy for Combining Harvesting of Predator and Prey. Natural Resource Modeling, 3, 63-90.
https://doi.org/10.1111/j.1939-7445.1988.tb00058.x - 11. Mesterton-Gibbons, M. (1996) A Technique for Finding Optimal Two-Species Harvesting Policies. Ecological Modelling, 92, 235-244.
https://doi.org/10.1016/0304-3800(95)00176-X - 12. Pahari, U.K. and Kar, T.K. (2013) Conservation of a Re-source Based Fishery through Optimal Taxation. Nonlinear Dynamics, 72, 591-603.
https://doi.org/10.1007/s11071-012-0737-z - 13. Huo, H.F., Jiang, H.M. and Meng, X.Y. (2012) A Dynamic Model for Fishery Resource with Reserve Area and Taxation. Journal of Applied Mathematics, 2012, Article ID: 794719.
https://doi.org/10.1155/2012/794719 - 14. Kar, T.K., Pahari, U.K. and Chaudhuri, K.S. (2004) Management of a Single Species Fishery with Stage Structure. International Journal of Mathematical Education in Science and Technology, 35, 403-414.
https://doi.org/10.1080/00207390410001686562 - 15. Dubey, B., Sinha, P. and Chandra, P. (2003) A Model for an Inshore-Offshore Fishery. Journal of Biological Systems, 11, 27-41.
https://doi.org/10.1142/S0218339003000725 - 16. Ganguly, S. and Chaudhuri, K.S. (1995) Regulation of a Sin-gle-Species Fishery by Taxation. Ecological Modelling, 82, 51-60.
https://doi.org/10.1016/0304-3800(94)00079-W - 17. Kar, T.K. (2005) Conservation of a Fishery through Optimal Taxation: A Dynamic Reaction Model. Communications in Nonlinear Science and Numerical Simulation, 10, 121-131.
https://doi.org/10.1016/S1007-5704(03)00101-1