Pure Mathematics
Vol.
09
No.
09
(
2019
), Article ID:
33127
,
15
pages
10.12677/PM.2019.99131
Explicit-Implicit and Implicit-Explicit Difference Methods and Numerical Analysis for Riemann-Liouville Type Fractional Diffusion Equation
Lifei Wu, Jiake Sun, Xiaozhong Yang*
School of Mathematics and Physics, North China Electric Power University, Beijing
Received: Nov. 1st, 2019; accepted: Nov. 18th, 2019; published: Nov. 25th, 2019

ABSTRACT
For the Riemann-Liouville (R-L) type fractional differential equations describing sub-diffusion phenomena, a kind of explicit-implicit and implicit-explicit difference schemes for numerically solving this problem is constructed. It takes advantage of the fast computation of explicit formats and the unconditional stability of implicit formats, alternatingly applies the classical explicit format and the implicit format by time layer. Then, using the Fourier method analysis, the format is unconditionally stable and convergent. The numerical test results are consistent with the theoretical analysis results, and show that the computational efficiency of the explicit-implicit and implicit-explicit formats is better than the classical implicit format. The explicit-implicit and implicit-explicit methods are feasible to solve the R-L fractional diffusion equation.
Keywords:R-L Fractional Diffusion Equation, Explicit-Implicit and Implicit-Explicit Scheme, Fourier Method, Stability, Convergence
Riemann-Liouville型分数阶扩散方程的显–隐和隐–显差分方法及数值分析
吴立飞,孙嘉科,杨晓忠*
华北电力大学数理学院,北京
收稿日期:2019年11月1日;录用日期:2019年11月18日;发布日期:2019年11月25日

摘 要
针对描述慢扩散现象的Riemann-Liouville (R-L)型分数阶扩散方程,构造了求解该问题的一类显–隐和隐–显差分格式。它是利用显式格式快速计算和隐式格式无条件稳定的优点,按时间层交替使用古典显式格式和隐式格式而得。使用傅里叶方法分析可知该格式为无条件稳定且收敛的。数值试验结果与理论分析结果一致,表明显–隐和隐–显格式的计算精度和计算效率均优于经典隐式格式,证实本文显–隐和隐–显格式对求解R-L型分数阶慢扩散方程是有效的。
关键词 :R-L型分数阶扩散方程,显–隐和隐–显格式,傅里叶方法,稳定性,收敛性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分数阶微分方程产生于一些反常扩散模型,有着深入的物理背景和丰富的理论意义。其特点在于它反映的不仅是局部或某个点的性质或数量,还考虑了历史以及非局部分布式的影响 [1] [2] [3]。在分数阶反常扩散模型中,时间分数阶导数主要刻画反常扩散过程具有的历史依赖性和路径依赖性,空间分数阶导数主要描述扩散过程的非局域特征,它们被用于许多物理、化学过程的数学建模中 [4]。
分数阶微分算子已成为一个描述各种复杂力学行为的重要工具。由于分数阶微分方程的解析解大多很难显式给出,因此研究解决分数阶微分方程的数值解法是必要且具有实际工程意义的 [5] [6]。近些年对于各类分数阶扩散方程的数值解法,已有不少的研究成果 [7] [8] [9] [10]。Wang Hong等对于空间分数阶扩散方程,根据所建立差分格式的特殊结构,提出了快速求解算法 [11]。崔明荣对具有非局部边界条件的时间分数阶扩散方程,考虑了两种不同的时间导数,即Caputo导数和Riemann-Liouville (R-L)导数,构造了其四阶紧致差分格式 [12]。张亚楠等提出了一种求解分数阶慢扩散方程的Crank-Nicolson型差分格式,并对其截断误差进行了详细分析 [13]。刘发旺等对一类多项分数阶波–扩散方程,提出了一些计算有效的隐式数值方法;数值结果表明了理论分析的有效性,这些方法和技术也可以推广到其他具有分数拉普拉斯的多项分数阶时空模型 [14]。吴立飞等给出时间Caputo型分数阶慢扩散方程的交替分段C-N差分格式,将经典C-N格式与四类非对称格式交替使用,提高算法的计算效率 [15]。陈昌明等人根据对分数阶导数的不同定义,利用傅里叶方法证明了显式及隐式格式的稳定性,同时结合外推技术构造了一类高精度算法 [16]。陈昌明等对具有非齐次强迫项的R-L型分数阶导数广义二阶流体的斯托克斯第一问题,构造其隐式差分格式,并分析格式的稳定性、收敛性 [17];最后数值试验验证了算法的有效性。高广花和孙志忠对分数阶扩散方程构造了一类紧致差分格式,并用能量法证明了格式无条件稳定以及精度为时间(2-a)阶,空间四阶收敛 [18]。
分数动力学方程已被证实在描述反常扩散(慢扩散)的情况下特别适用。近几年,分数扩散方程的理论证明以及丰富的物理和生物实验验证了反常扩散现象的普遍性;对于反常慢扩散随机游走模型,以分数阶慢扩散方程代替了原来的常规扩散方程,提出描述反常扩散粒子遵循分数阶扩散方程 [1] [2] [3]:
. (1)
其中 是概率密度函数, 表示 的 阶R-L型分数阶导数,
.
针对此问题,Langlands和Henry构造了隐式格式(L1近似),并讨论了格式的稳定性和收敛性 [19];此后,刘发旺等使用傅里叶分析法,分析了对 情形下隐式格式的稳定性和收敛性,以及全局精度 [16] [17]。但是由于分数阶导数的非局部性,分数阶扩散方程数值模拟的计算量和存储量极大,即便使用高性能计算机,也很难进行长时间历程或大计算域的模拟。对于这个问题,本文尝试使用经典显式格式和隐式格式交替使用的方法来提高数值模拟的计算效率 [20] [21],即对分数阶次扩散模型构造显–隐(E-I)和隐–显(I-E)格式;理论分析和数值试验表明,显–隐和隐–显格式的计算效率和计算精度均优于隐式差分格式。
2. 分数阶扩散方程显–隐和隐–显方法
2.1. R-L型时间分数阶扩散方程
本文主要考虑描述慢扩散现象的R-L型分数阶扩散方程的初边值问题 [2] [3] [4]
. (2)
初始条件为: ,
边值条件为: 。
其中 , 、 、 、 都是足够光滑的函数。
给出方程(2)式两边作积分 运算,可得
,(3)
上式等价为
, (4)
由文献 [3] 可知,如果 ,则有
.
即(4)式为
(5)
2.2. 显–隐和隐–显格式的构造
令 ,,,。定义网格函数
, , , .
定义如下记号: 。
定义离散分数阶导数算子
, .
引理1 [6] 假设 ,,有
.
时间分数阶慢扩散方程的隐式格式为:
,(6)
时间分数阶慢扩散方程的显式格式为:
. (7)
初始、边界条件相应离散为:
经典显式格式为条件稳定的,其优点是可以显式快速计算;而隐式格式为无条件稳定,但需要求解代数方程组,计算效率较低。结合两种差分格式的优点,在时间层上交替使用,可得显–隐和隐–显差分格式。
分数阶慢扩散方程的显–隐式格式为:
(8)
同理,可构造分数阶慢扩散方程的隐–显格式为
(9)
其中 。
3. 显–隐和隐–显方法的稳定性分析
首先分析时间分数阶慢扩散方程的显–隐格式的稳定性,其显–隐格式可以写成如下形式:
(10)
其中 。
设 是显–隐格式的近似解,定义 和 ,代入(10)式可得如下误差扰动方程:
(11)
下面使用Fourier方法分析显–隐格式的稳定性。在此,定义网格函数
的Fourier展开形式为:
,
其中系数 。
另外,离散2模的定义
(12)
应用Parseval等式,有
,即 .
基于上面的分析,假设(11)式有如下形式的波动解 ,其中 。
当 时(m是时间层数),我们使用显式差分格式,有
,
,
由 ,可得
, (13)
当 时,第一层使用显式格式,第二层使用隐式格式,
,
,
联立两式,可得
,
.(14)
当 时,假设 成立;当 ,有
两式结合,消去 项,可得
令 ,由上式可得
. (15)
综上分析,有如下定理
定理1 R-L型分数阶扩散方程的显–隐格式是无条件稳定的。
证明:由(13,14,15)式,可知
.
因此,分数阶扩散方程的显–隐格式是稳定的,定理1证毕。
同理,可有
定理2 R-L型分数阶扩散方程的隐–显格式是无条件稳定的。
4. 显–隐和隐–显方法的收敛性分析
引理2 [13] 假设 ,,有
(16)
引理3 [15] ,C是常数。
首先分别分析显–隐格式(8)中,显式格式和隐式格式的截断误差。
, (17)
可知,当q = 0时,为显式格式,当q = 1时,为隐式格式。定义截断误差
(18)
(19)
由引理3可得
因此,存在正数 使得
, . (20)
定义
.
和
, .
下面使用Fourier方法分析显–隐格式的收敛性。在此,定义网格函数
和
的Fourier展开形式为:
,其中系数 。
,其中系数 。
同样,关于离散2模,有
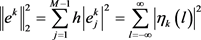 ,(21)
,(21)
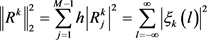 . (22)
. (22)
基于上面的分析,假设 ,
, ,其中
,其中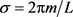 ,可得
,可得
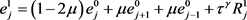 ,
,
 ,
,
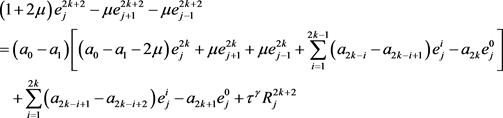 (23)
(23)
引理4 设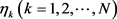 是方程(23)的解,存在一个正数
是方程(23)的解,存在一个正数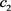 ,使得
,使得
 .
.
证明:由定义,可知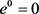 ,有
,有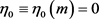 。
。
另外,由(20)式和(22)式可知
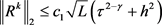 (24)
(24)
(22)式等式右边的系数数列是收敛的,因此存在一个正数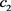 使得
使得
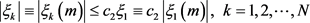 . (25)
. (25)
因此有
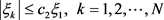 .
.
参考稳定性证明,使用数学归纳法可得
当 时,
时,
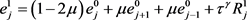 ,
,
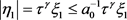 ,
,
当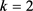 时,
时,
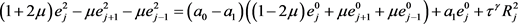 ,
,
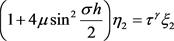 ,
,
 ,
,
假设
 .
.
由引理1,有
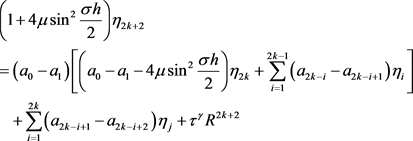
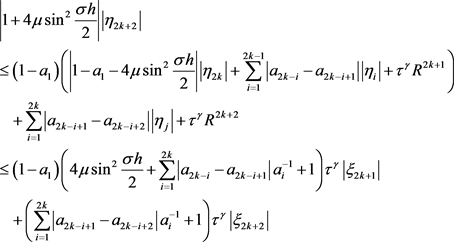
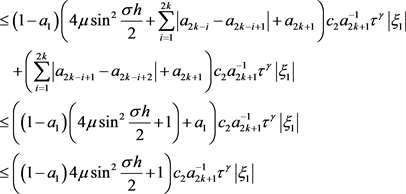
即
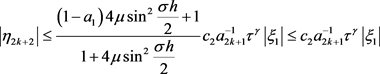 .
.
由于
 .
.
则存在正常数 ,使得
,使得
 .
.
综上,可有
定理3 R-L型分数阶扩散方程的显–隐格式是无条件收敛的,收敛阶是 .
.
证明:由引理4及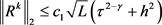 ,可得
,可得
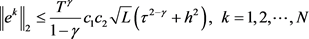 .
.
定理3证毕。
同理,可有
定理4 R-L型分数阶扩散方程的隐–显格式是无条件收敛的,收敛阶是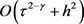 .
.
5. 数值试验
数值试验基于Intel Core i5-2400 CPU@3.10GHz,在MatlabR2014a环境下进行;我们将通过数值试验验证前面的理论分析。
例1. 非齐次R-L型分数阶扩散方程 [4] [16]
 .
.
其边界条件为: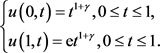
初始条件为: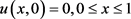 .
.
此时解析解为: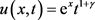 .
.

Figure 1. Surfaces of analytic solution and E-I, I-E scheme numerical solutions
图1. 解析解和隐–显、显–隐格式数值解的解曲面
取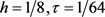 时,给出解析解、显–隐和隐–显格式的解曲面图1;可以看出解析解、显–隐和
时,给出解析解、显–隐和隐–显格式的解曲面图1;可以看出解析解、显–隐和
隐–显格式解曲面形状一致且光滑。解析解与差分格式解的最大模误差定义为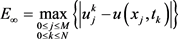 。
。
对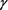 分别取0.1~0.9等不同值,取
分别取0.1~0.9等不同值,取 ,隐式格式、显–隐格式和隐–显格式三种数值格式的最大模误差情况见表1。由表1可知,隐式格式与显–隐和隐–显格式的精度相当;对不同
,隐式格式、显–隐格式和隐–显格式三种数值格式的最大模误差情况见表1。由表1可知,隐式格式与显–隐和隐–显格式的精度相当;对不同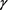 值隐式格式和显–隐格式的误差比较;可以看出当
值隐式格式和显–隐格式的误差比较;可以看出当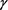 值大于0.5时,隐式格式的精度高于显–隐格式,当
值大于0.5时,隐式格式的精度高于显–隐格式,当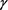 值小于0.5时,显–隐格式的精度优于隐式格式。随着
值小于0.5时,显–隐格式的精度优于隐式格式。随着 值得减小,显–隐格式和隐–显格式的误差越来越小;整数阶显–隐差分格式为二阶差分格式,其精度优于隐式格式。当
值得减小,显–隐格式和隐–显格式的误差越来越小;整数阶显–隐差分格式为二阶差分格式,其精度优于隐式格式。当 值接近于0时,显–隐格式和隐–显格式的特性接近整数阶的情形。
值接近于0时,显–隐格式和隐–显格式的特性接近整数阶的情形。
Table 1. Accuracy comparison analysis of three numerical schemes
表1. 三种数值格式的精度比较分析
下面,由最大模误差定义时间收敛阶 以及空间收敛阶
以及空间收敛阶 ,验证理论分析。固定空间步长h,时间收敛阶如下定义:
,验证理论分析。固定空间步长h,时间收敛阶如下定义: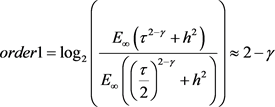 。固定时间步长
。固定时间步长 ,定义空间收敛阶如下:
,定义空间收敛阶如下: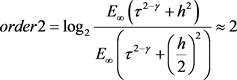 。
。
Table 2. Time direction convergence order of three difference schemes (h = 64)
表2. 三种差分格式的时间方向收敛阶(h = 64)
由表2,对不同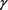 值,隐式格式与隐–显、显–隐格式在时间方向上的收敛阶为
值,隐式格式与隐–显、显–隐格式在时间方向上的收敛阶为 阶;隐式格式与显–隐格式、隐–显格式的精度也相当。由表3可看出,对不同
阶;隐式格式与显–隐格式、隐–显格式的精度也相当。由表3可看出,对不同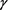 值,隐式格式和隐–显、显–隐格式在空间上的收敛阶均为2阶,与理论分析一致。
值,隐式格式和隐–显、显–隐格式在空间上的收敛阶均为2阶,与理论分析一致。
例2. 齐次R-L型分数阶扩散方程 [4] [16]
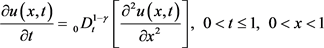 .
.
其边界条件为: ,
,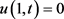 ,
,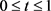 。
。
初始条件为: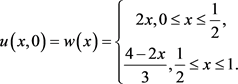
其中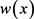 表示由点
表示由点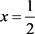 处热源产生的棒的温度分布。
处热源产生的棒的温度分布。
Table 3. Spatial direction convergence order of three difference schemes under different
表3. 三种差分格式的空间方向收敛阶
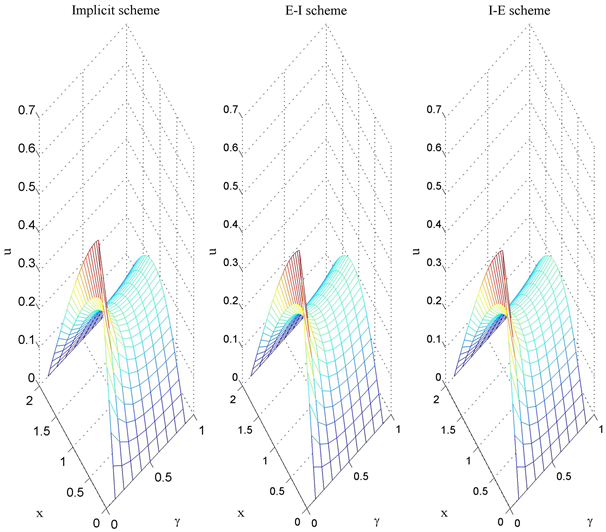
Figure 2. Surface of numerical solution of three different schemes for different 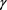
图2. 三种差分格式的解曲面
Table 4. Comparison of calculation times for three differential schemes (unit: s)
表4. 三种差分格式计算时间的比较(单位:s)
当初始条件为分段函数,取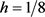 ,
,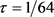 ,
, ,
, 取不同值时,隐式格式、显–隐和隐–显格式的解曲面图2;由图2可知隐式格式和显–隐(隐–显)格式解形状一致,且光滑,说明显–隐和隐–显差分格式对求解例2问题的有效性。由表4可知,隐–显格式和显–隐格式的计算时间相当,但是随着网格数的增加,隐式格式与显–隐和隐–显格式相比,计算时间增加的速度越来越快;其趋势在图3中可见。可见对于求解分数阶慢扩散模型,显–隐和隐–显格式与隐式格式相比,在计算效率方面有明显的改进。
取不同值时,隐式格式、显–隐和隐–显格式的解曲面图2;由图2可知隐式格式和显–隐(隐–显)格式解形状一致,且光滑,说明显–隐和隐–显差分格式对求解例2问题的有效性。由表4可知,隐–显格式和显–隐格式的计算时间相当,但是随着网格数的增加,隐式格式与显–隐和隐–显格式相比,计算时间增加的速度越来越快;其趋势在图3中可见。可见对于求解分数阶慢扩散模型,显–隐和隐–显格式与隐式格式相比,在计算效率方面有明显的改进。
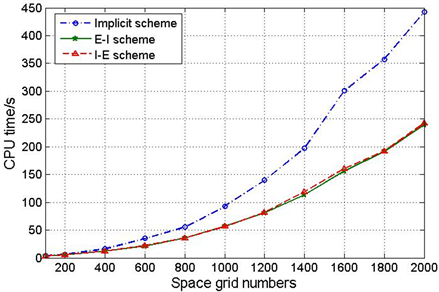
Figure 3. Comparison of calculation times for three differential schemes
图3. 三种差分格式的计算时间比较
6. 结论
本文对R-L型分数阶扩散方程,构造了其显–隐和隐–显差分格式;通过傅里叶方法对构造格式进行了理论分析,得出显–隐和隐–显格式均为无条件稳定和收敛的,通过数值试验证实了理论分析。交替使用显式、隐式两个古典格式,可以使算法计算复杂度得到下降。由数值试验可知,显–隐和隐–显格式的计算精度与隐式格式相当,但计算效率与隐式格式相比有着明显的提高;表明显–隐和隐–显格式对求解R-L型分数阶扩散方程是有效的。
基金项目
国家科技重大专项子课题(2017ZX07101001-01),中央高校基金科研业务专项资金资助(2018MS168)。
文章引用
吴立飞,孙嘉科,杨晓忠. Riemann-Liouville型分数阶扩散方程的显–隐和隐–显差分方法及数值分析
Explicit-Implicit and Implicit-Explicit Difference Methods and Numerical Analysis for Riemann-Liouville Type Fractional Diffusion Equation[J]. 理论数学, 2019, 09(09): 1060-1074. https://doi.org/10.12677/PM.2019.99131
参考文献
- 1. Uchaĭkin, V.V. (2013) Fractional Derivatives for Physicists and Engineers, Volume I: Background and Theory. Springer, Berlin. https://doi.org/10.1007/978-3-642-33911-0
- 2. Uchaĭkin, V.V. (2013) Fractional Derivatives for Physicist and Engineers, Volume II: Applications. Springer, Berlin. https://doi.org/10.1007/978-3-642-33911-0
- 3. Guo, B.L., Pu, X.K., Huang, F.H., et al. (2015) Fractional Partial Differential Equations and Their Numerical Solutions. Science Press, Beijing. https://doi.org/10.1142/9543
- 4. 陈文, 孙洪广. 反常扩散的分数阶微分方程和统计模型[M]. 北京: 科学出版社, 2017.
- 5. 刘发旺, 庄平辉, 刘青霞. 分数阶偏微分方程数值方法及其应用[M]. 北京: 科学出版社, 2015.
- 6. 孙志忠, 高广花. 分数阶微分方程的有限差分方法[M]. 北京: 科学出版社, 2015.
- 7. Li, X.J. and Xu, C.J. (2009) A Space-Time Spectral Method for the Time Fractional Diffusion Equation. Siam Journal on Numerical Analysis, 47, 2108-2131. https://doi.org/10.1137/080718942
- 8. Zeng, F.H., Li, C.P., Liu, F.W., et al. (2013) The Use of Finite Difference/Element Approaches for Solving the Time Fractional Sub-Diffusion Equation. SIAM Journal on Scientific Computing, 35, A2976-A3000. https://doi.org/10.1137/130910865
- 9. Lv, C.W. and Xu, C.J. (2015) Improved Error Estimates of a Finite Difference/Spectral Method for Time-Fractional Diffusion Equations. International Journal of Numerical Analysis & Modeling, 12, 384-400.
- 10. 杨莹莹, 李景. 空间分布阶时间分数阶扩散方程的有限体积法[J]. 理论数学, 2019, 9(3): 351-361.
- 11. Wang, H. and Wang, K.X. (2011) An O(N log2N) Alternating-Direction Finite Difference Method for Two-Dimensional Fractional Diffusion Equations. Journal of Computational Physics, 230, 7830-7839. https://doi.org/10.1016/j.jcp.2011.07.003
- 12. Cui, M.R. (2018) Com-pact Finite Difference Schemes for the Time Fractional Diffusion Equation with Nonlocal Boundary Conditions. Computational & Applied Mathematics, 37, 3906-3926. https://doi.org/10.1007/s40314-017-0553-7
- 13. Zhang, Y.N., Sun, Z.Z. and Wu, H.W. (2011) Error Estimates of Crank-Nicolson-Type Difference Schemes for the Sub-Diffusion Equation. SIAM Journal on Numerical Analysis, 49, 2302-2322. https://doi.org/10.1137/100812707
- 14. Liu, F.W., Meerschaert, M.M., Mcgough, R.J., et al. (2013) Numerical Methods for Solving the Multi-Term Time-Fractional Wave-Diffusion Equation. Fractional Calculus & Applied Analysis, 16, 9-25. https://doi.org/10.2478/s13540-013-0002-2
- 15. Wu, L.F., Yang, X.Z. and Cao, Y.H. (2018) An Alternating Segment Crank-Nicolson Parallel Difference Scheme for the Time Fractional Sub-Diffusion Equation. Advances in Difference Equations, 2018, 287. https://doi.org/10.1186/s13662-018-1749-x
- 16. Chen, C.M., Liu, F.W., Turner, I., et al. (2007) A Fourier Method for the Fractional Diffusion Equation Describing Sub-Diffusion. Journal of Computational Physics, 227, 886-897. https://doi.org/10.1016/j.jcp.2007.05.012
- 17. Chen, C.M., Liu, F.W. and Anh, V. (2009) A Fourier Method and an Extrapolation Technique for Stokes’ First Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative. Journal of Computational and Applied Mathematics, 223, 777-789. https://doi.org/10.1016/j.cam.2008.03.001
- 18. Gao, G.H. and Sun, Z.Z. (2017) Two Difference Schemes for Solving the One-Dimensional Time Distributed-Order Fractional Wave Equations. Numerical Algorithms, 74, 675-697. https://doi.org/10.1007/s11075-016-0167-y
- 19. Langlands, T.A.M. and Henry, B.I. (2005) The Accuracy and Stability of an Implicit Solution Method for the Fractional Diffusion Equation. Journal of Computational Physics, 205, 719-736. https://doi.org/10.1016/j.jcp.2004.11.025
- 20. 孙志忠. 非线性发展方程的有限差分方法[M]. 北京: 科学出版社, 2018.
- 21. 张锁春. 抛物型方程定解问题的有限差分数值计算[M]. 北京: 科学出版社, 2010.
NOTES
*通讯作者。
