Pure Mathematics
Vol.
11
No.
08
(
2021
), Article ID:
44656
,
6
pages
10.12677/PM.2021.118169
最大度大于等于八的可嵌入图的全染色
王丽婷*,王慧娟#
青岛大学数学与统计学院,山东 青岛
收稿日期:2021年7月9日;录用日期:2021年8月12日;发布日期:2021年8月19日

摘要
图的染色问题是图论中的一个重要研究方向,在计算机科学,组合优化和网络优化等方面有非常重要的应用,全然色是一种重要的染色。本文利用权值转移的方法证明了,如果G是最大度大于等于八的可嵌入到欧拉示性数非负曲面的图,且G中不包含相邻的4-圈,那么图G的全色数等于最大度加一。
关键词
欧拉示性数,曲面,全染色,权转移方法

Total Coloring of Embedded Graphs with Maximum Degree at Least Eight
Liting Wang*, Huijuan Wang#
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Jul. 9th, 2021; accepted: Aug. 12th, 2021; published: Aug. 19th, 2021

ABSTRACT
Graph coloring is an important research direction in graph theory. It has very important applications in computer science, combination optimization and network optimization. Total coloring is an important type of coloring. In this paper, we use the discharging method to prove that if G is a graph of maximum degree that is equal or greater than eight, and it can be embedded into a nonnegative surface of Euler characteristic, and G does not contain adjacent 4-cycles, then the total chromatic number of G is equal to its maximum degree plus one.
Keywords:Euler Characteristic, Surface, Total Coloring, Discharging Method

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文仅考虑可嵌入到欧拉示性数非负的曲面的图,且这些图是无向的、有限的,简单的且非空的图。文中未加定义直接使用的概念和符号可以参考文献 [1]。分别用 ,, 表示图的点集,面集和边集。设 ,则v的度数 是与v相关联的边的个数。 代表图G的最大度,即 ,简写为 。同样的,图G的面f的度数 是面的边界所含边的个数。如果图G中存在连接顶点u和v的路,则称这两个顶点是连通的。若图G的任意两个顶点是连通的,则称图G是连通图。如果存在V的子集 ,使得 不连通,则称是 是G的顶点割。k-顶点割是包含k个元素的顶点割,G中所有具有k顶点割中最小的k,称为G的连通度,记作 。如果 ,则称G是k-连通的。一个图G的k-全染色,是指从集合 到集合 的一个映射,使得在集合 的任意两个相邻或相关联的元素的值不相等。如果可以用k种颜色对图G全染色,那么则称图G是k-可全染色的,使得图G是k-可全染色的最小正整数k称为图G的全色数 。
猜想1 对于任意的简单图G都有, 。
这个猜想称为全染色(TCC)猜想,在20世纪60年代,由Vizing [2] 和Behzad [3] 分别独立提出。全染色猜想在 时,对于一般图成立,而对于平面图,当 时,尚未完全证明 [4],本文中考虑的图G是可以嵌入到欧拉示性数非负的曲面上的图,即 。对于可以嵌入到欧拉示性数 的曲面上的图,Zhao Y.证明了当 时,全染色猜想成立 [5],Wang H. J.和Liu B.将结果推广到 [6]。Wang Y.对可嵌入到欧拉示性数非负曲面的图的全染色进行完善 [7]。随着研究的深入,人们发现一些图的全色数不仅仅满足全染色猜想,还有更强的结论,即 。Wang B.和Wu J. L.证明了当 ,且不含相邻3-圈和4-圈时 [8]。

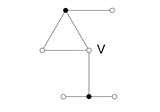
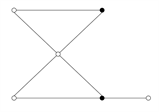
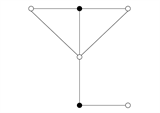
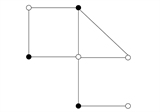
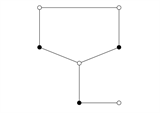
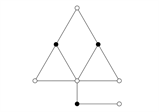
Figure 1. Forbidden structure of subgraph.
图1. 禁用子图结构
2. 引理
引理1 [9] G是2-连通的。
引理2 [10] 如果 且 那么 。
引理3 [11] 图G中连接2-点与8-点的边导出的子图是森林。
引理4 [12] 图G中不包含同构于如图1的禁用子图结构。(图中实心点表示已经画出与其关联的所有边,空心点表示没有画出与其关联的所有边。图中 。)
3. 主要结果的证明
基于以上引理,下面开始证明我们的主要结论。
定理1 设G是 可嵌入到欧拉示性数非负曲面的图,且G中不包含相邻的4-圈,那么图G的全色数 。
为方便证明下面给出一些定义和符号。在图G中,令k-点,k−-点,k+-点分别表示在图G中度数等于k的点,度数小于等于k的点,度数大于等于k的点。类似的,我们可以定义k-面,k−-面,k+-面。令 代表与v相邻的k-点的个数,类似的可以定义, ,。令 代表与v相关联的k-面的个数,类似的可以定义, ,。
由于图G是可以嵌入到欧拉示性数非负曲面上的图,所以由Euler公式 得,
假设图G是满足定理条件的一个极小反例。首先定义初始权值,对于任意的 ,设初始权值为 ,对于任意的 ,设初始权值为 。然后对于任意的 按照权转移规则对权值重新分配得到新的权值 ,由于权转移规则只是移动权值,而不会改变权值的总和,所以转移后的权值总和小于等于0。即
需要验证,对权值进行重新分配后,对于任意的 ,都有 ,并且当 ,有 ,由于在文献 [13] 中, 已经证明过此结论,所以只需要证明当 时,有 ,那么得出转移后的权值总和严格大于0,得出矛盾,所以不存在这样的反例,即定理成立。
接下来给出如下的权值转移规则。要注意的是,权转移是在相邻的点之间,或者相关联的面之间进行转移。
R1 2-点从两个邻点各得1。
R2 4-点给3-面或4-面 ,给5-面 。
R3 5-点给3-面1,给4-面 ,给5-面 。
R4 6-点给3-面 ,给4-面 ,给5-面 。
R5 7+-点给与3−点关联的3-面 ,给不与3−点关联的3-面1,给与两个3−-点关联的4-面1,给其余的4-面 ,给5-面 。
现在开始验证,对于任意的 ,设 ,则 。设 ,则f至多与两个3−-点相邻,即f至少与三个4+-点相邻。所以 。设 ,当f与两个3−-点关联,则f与两个7+-点关联,所以 。当f与一个3−-点,两5−-点相关联,f与两个7+-点相关联,所以 。当f不与一个3−-点相关联,则 。设 ,当f与3−-点关联,则f与两个7+-点相关联,所以 当f不与3−-点关联,则 。
对于任意的 ,设 ,则由R1, 。设 ,则 。设 ,则由R2, 。设 ,则 ,则由R3, 。设 ,则 ,当 ,则 ,由R4, 。当 ,。设 ,则 ,当 ,则 ,,所以 。当 ,则 ,所以 。
设 ,则 ,下面开始分情况讨论。
情形1 ,则 。
当 ,则 ,所以 。当 ,则 。若 ,则 ,所以至多有两个4-面关联两个3−-点,所以 。若 ,则 。
情形2 ,则 。
当 ,则 ,所以 。当 ,若v关联两个相邻的3-面时,则 ,所以 。若与v关联的4个3-面两两不相邻,则 ,所以 。当 ,则 ,所以 。
情形3 ,则 。
当 ,则 ,所以 。当 ,若v关联两个相邻的3-面时,则 ,所以 。若与v关联的3-面两两不相邻,则点v关联的4-面至多关联一个3−-点,所以 。当 ,则 ,所以 。
情形4 ,则 。
当 ,则 ,,,且点v关联的4-面至多关联一个3−-点,所以 。当 ,则 ,若 ,则与点v关联的4-面中至少有一个四面至多关联一个3−-点,所以 。若 ,则 。
情形5 ,则 。
当 ,则 。若 ,则点v不与3−-点相邻,所以 。若 ,则与点v关联的4-面中至少有两个4-面至多关联一个3−-点,所以 。
当 ,则 ,且 。若 ,则 ,且与点v关联的4-面中至少有两个4-面至多关联一个3−-点,所以 。若 ,则 ,所以 。当 ,则 ,所以 。
情形6 ,则 。
当 ,则 ,且 ,所以 。
当 ,则 ,且 ,所以 。
当 ,则 ,且 ,所以 。
情形7 ,则 。
当 ,则 ,且 ,所以 。
当 ,则 ,且 ,所以 。
情形8 ,则 ,且 ,,所以 。
至此,定理的证明完成。
基金项目
本课题由山东省自然科学基金:ZR2020MA045资助。
文章引用
王丽婷,王慧娟. 最大度大于等于八的可嵌入图的全染色
Total Coloring of Embedded Graphs with Maximum Degree at Least Eight[J]. 理论数学, 2021, 11(08): 1505-1510. https://doi.org/10.12677/PM.2021.118169
参考文献
- 1. Bondy, J.A. and Murty, U.S.A. (1976) Graph Theory with Applications. MacaMillan, London, 1-197. https://doi.org/10.1007/978-1-349-03521-2_1
- 2. Behzad, M. (1965) Graphs and Their Chromatic Numbers. Michigan State University, Michigan.
- 3. Vizing, V.G. (1968) Some Unsolved Problems in Graph Theory. Uspekhi Matematicheskikh Nauk, 23, 117-134. https://doi.org/10.1070/RM1968v023n06ABEH001252
- 4. Kostochka, A.V. (1996) The Total Chromatic Number of Any Multigraph with Maximum Degree Five Is at Most Seven. Discrete Mathematics, 162, 199-214. https://doi.org/10.1016/0012-365X(95)00286-6
- 5. Zhao, Y. (1999) On the Total Coloring of Planar Graphs Embeddable in Surfaces. Narnia, 60, 333-341. https://doi.org/10.1112/S0024610799007668
- 6. Wang, H.J. and Liu, B. (2014) Total Coloring of Embedded Graphs with Maximum Degree at Least Seven. Theoretical Computer Science, 518, 1-7. https://doi.org/10.1016/j.tcs.2013.04.030
- 7. 王颖. 嵌入到欧拉示性数非负曲面上的图的全染色[D]: [硕士学位论文]. 济南: 山东大学, 2014.
- 8. Wang, B. and Wu, J.L. (2018) Total Coloring of Embedded Graphs with No 3-Cycles Adjacent to 4-Cycles. Discusions mathematicae Graph Theory, 38, 978-983. https://doi.org/10.7151/dmgt.2058
- 9. Borodin, O.V. (1989) On the Total Coloring of Planar Graphs. Journal für die reine und angewandte Mathematik, 394, 180-185. https://doi.org/10.1515/crll.1989.394.180
- 10. Hou, J.F. and Zhu, Y. (2008) Total Coloring of Planar Graphs without Small Cycles. Graphs and Combinatorics, 24, 91-100. https://doi.org/10.1007/s00373-008-0778-8
- 11. Wang, W.F. (2007) Total Chromatic Number of Planar Graphs with Maximum Degree Ten. Graph Theory, 54, 91-102. https://doi.org/10.1002/jgt.20195
- 12. Kowalik, L. and Sereni, J.S. (2008) Total Coloring of Plane Graphs with Maximum Degree Nine. Discrete Mathematics, 22, 1462-1479. https://doi.org/10.1137/070688389
- 13. 王慧娟. 可嵌入图的染色问题[D]: [博士学位论文]. 济南: 山东大学. 2015.
NOTES
*第一作者。
#通讯作者。