公钥加密算法与抗量子密码体制安全性的数学分析 Mathematical Analysis of Public Key Encryption Algorithm and Security of Anti Quantum Cryptography

doi:10.12677/AAM.2018.710147

Advances in Applied Mathematics
Vol. 07 No. 10 ( 2018 ), Article ID: 27244 , 12 pages
10.12677/AAM.2018.710147

Mathematical Analysis of Public Key Encryption Algorithm and Security of Anti Quantum Cryptography

Biaogaoze Tang¹, Wanze Huang¹, Hongan Zhao¹, Yongzhan Hu², Zhengzheng Yan¹, Hongxin Li^1,3*

●How to Cite this Article

¹PLA Strategic Support Force Information Engineering University, Luoyang Henan

²Zhengzhou Audit Center, Zhengzhou Henan

³State Key Laboratory of Cryptology, Beijing

Received: Oct. 1^st, 2018; accepted: Oct. 17^th, 2018; published: Oct. 24^th, 2018

ABSTRACT

The public key system encryption algorithm based on the difficult problem of mathematics is faced with the challenge of the improving computing power of computers. How to keep the safety of mathematical problems and optimize the theoretical basis of the existing public key encryption, analyze and verify the reliability and practicability of quantum-resistant cryptography from the perspective of mathematics, and further advance encryption technology have been an important research direction in cryptography and computer science. By reviewing mathematical problems such as integer factorization and the difficulty of solving the discrete logarithm problem, and by following research trends, this paper analyzes the mathematical foundation of public key cryptography, and verifies the reliability of quantum-resistant cryptography. This is of practical significance to effectively cope with the threat of the forthcoming quantum computing to the public key cryptosystem.

Keywords:Public Key Encryption, Integer Factorization, Discrete Logarithm, Shortest Vector Problem, Subset Problem

公钥加密算法与抗量子密码体制安全性的数学分析

唐彪高泽¹，黄婉泽¹，赵洪安¹，胡勇战²，闫争争¹，李宏欣^1,3*

¹中国人民解放军战略支援部队信息工程大学，河南洛阳

²郑州审计中心，河南郑州

³密码科学技术国家重点实验室，北京

收稿日期：2018年10月1日；录用日期：2018年10月17日；发布日期：2018年10月24日

摘要

基于数学难解问题的公钥体制加密算法面临着计算机计算能力进步的挑战，如何优化现有公钥加密理论基础、从数学角度分析验证抗量子密码的安全性与实用性，进而推进密码学加密技术的进步，一直是密码学与计算机科学的主要攻坚方向。本文通过回顾大数分解、对数难解等数学难题分析公钥密码的数学基础，同时结合科研动态从数学理论出发验证抗量子公钥密码体制的可靠性。这对有效应对即将到来的量子计算对公钥密码体制的威胁具有现实意义。

关键词 :公钥加密，大数分解，离散对数，最短格矢问题，子集和问题

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

经典密码体系下的公钥加密算法、抗量子加密算法与基于量子理论物理学的量子密码加密算法是接下来一段时期内信息安全与保密通信领域主要的研究内容之一。从国防信息安全到商业、银行业应用，加密算法对国家安全、社会基本秩序与经济发展有着重要且基础性的巨大作用。

基于数论中的大数分解难解问题与椭圆曲线中的离散对数难解问题，密码学家们创造了单向陷门函数为主体的现代公钥密码体系。但是，面对可预见的量子计算机的研究和构建，基于计算复杂度的密码体系都是不安全的 [1] 。

由于纯粹的量子通信技术在实现上存在着许多技术难题，经典密码中的公钥密码体系仍然是今后一个时期内安全性最高和应用最为普遍的加密方式。面对量子计算不断发展带来的严峻密码破译威胁与网络安全、信息安全威胁，通过量子密钥分配加强基于数学难题的经典密码中密码理论实现的安全性成为当前抗量子密码加密算法的主要研究方向。不过，其数学难题的难解程度始终是保护公钥密码体系安全性的核心。

本文第二节首先回顾经典公钥密码RSA算法与其安全性；之后第三节从随机数、大数难解问题、离散对数难解问题和椭圆曲线上的离散对数难解问题的角度分析其安全性的数学基础；在第四节中正视量子计算危机的同时也看到量子计算的短板，并针对基于子集和问题构架的OUT量子公钥密码算法与基于最短格矢问题的NTRU公钥密码算法进行抗量子安全性的分析。希望借此为基于抗量子公钥加密、量子密钥传输和严格单向函数的密码加密学提供研究方向参考。

2. 公钥加密算法

上世纪七十年代，对称密码体制的缺点随着通信网络的发展而逐渐凸显，公开密钥加密算法体制的提出是为了解决对称密码体制的密钥分发问题和电子签名的问题。

2.1. 公钥加密典型算法基本原理

公钥密码的典型构造是基于陷门单向函数的，即正向求解容易实现而反向逆求解十分困难甚至在现有技术条件下不可能实现 [2] 。公钥密码体系中有很多的具体算法，如早期的RSA算法、Rabin算法、和后来的ElGamal算法、椭圆曲线算法。从原理上看，它们相当一致，而且十分简单，都具有密钥由两个部分组成和数学上的潜在相关性的共同点。其中，著名的RSA算法是较早提出、使用时间最长、应用范围最广公钥算法。

2.1.1. RSA加密算法

基本过程

RSA加密算法的理论基础是一种特殊的可逆模指数运算，首先把明文信息通过某种算法(最好是随机数算法使其具备统计学上的随机性)转化成一组数，将此作为明码对其进行加密。

过程如下：

1) 在保密的情况下找两个大而互异的素数(质数) $P, Q$ 。计算， $φ (N) = (P - 1) (Q - 1)$ 。

2) 找一个与 $φ (N)$ 互素的整数 $E$ 。

3) 找一个整数 $D$ ，使 $E D = 1 \mod (P - 1) (Q - 1)$ 。

4) 公开密钥 $= (N, E)$ ，私有密钥 $= (N, D)$ 。

其中，联系公钥和私钥的乘积 $N$ 为模数，是通信双方都知道的； $E$ 作为用于加密运算的指数，发送方是必须知道；而 $D$ 为用于解密运算的指数，只有接收方知道。

用下面的公式对明码 $X$ 进行加密，得出密码 $Y$ 。

$X^{E} \mod N = Y$

接收方在收到密码 $Y$ 之后，依据费马小定理，按照下面的公式解密读取明码。

$Y^{D} \mod N = X$

在没有私有密钥 $D$ 的情况下，难以通过密文 $Y$ 逆向求解出 $X$ ，因此这是一个基于大数分解难解问题的陷门单向函数。即想要破译整个密码，必须对大整数 $N$ 作素因子分解，而这在数学计算上是困难的。

数学推导

设定 $x$ 遍历 $φ (n)$ 的简化剩余系，那么 $e x$ 也遍历 $φ (n)$ 的简化剩余系，将存在某个 $x_{0}$ ，满足 $e x_{0} \equiv 1 (\mod φ (n))$ ，并且由于 $(1, φ (n)) = 1$ ， $1$ 是模数为 $φ (n)$ 的简化剩余系的一个代表。所以，取 $d = x_{0}$ ，就会得到 $e d \equiv 1 (\mod φ (n))$ 。

由同余性质，知 $e d = k φ (n) + 1$ ， $k \in Z$ 。

由， $(a, p) = 1$ ，根据欧拉定理， $a^{φ (p)} \equiv 1 (\mod p)$ ，则：

${(a^{φ (p)})}^{k φ (q)} \equiv {(1)}^{k φ (q)} (\mod p) \equiv 1 (\mod p)$

$a {(a)}^{k φ (p) φ (q)} \equiv a (\mod p)$

$a^{k φ (n) + 1} \equiv a (\mod p)$

$a^{e d} \equiv a (\mod p)$

由于素数 $(p, q) = 1$ ， $φ (p q) = φ (p) φ (q) = φ (n)$ 。对素数 $q$ ， $a^{e d} \equiv a (\mod q)$ 。又因为 $(p, q) = 1$ ，则：

$a^{e d} \equiv a (\mod p q) \equiv a (\mod n)$

$a^{e d} \equiv {(a^{e})}^{d} \equiv a (\mod n)$

$\dots$

$c^{d} \equiv a (\mod n)$

这里选取的是两个较大的素数，不等于2，于是它们也是奇数。加密过程中，先对明文进行分组，使每一组明文对应的数值小于 $n$ ，其中每组加密过程为

$C = E_{P K_{r}} [M] \Leftrightarrow c \equiv m^{e} (\mod n)$

对应的解密过程为

$M = D_{S K_{r}} [C] \Leftrightarrow m \equiv c^{d} (\mod n) \equiv {(m^{e})}^{d} (\mod n)$

2.1.2. Rabin加密算法数学推导

Rabin密码体制是对RSA密码体制的改进和修正 [3] 。设明文为M，密文为C，加密过程为，其中 $n = p q$ 为大整数。这是一个两次同余式，对应的解密过程为 $M = D_{S K_{r}} [C]$ ，转化成求这个二次同余式的平方根的问题，这个问题就转化成了C是否是这个二次同余式的二次剩余问题：因为 $C \equiv M^{2} (\mod n)$ ，而且 $n = p q$ ，于是等价于二次同余式组

${\begin{cases} M^{2} = C (\mod p) \\ M^{2} = C (\mod q) \end{cases}$

其中的 $p$ 和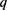都是大素数，同时也是奇数，此二次同余式组有解等价于 $C$ 是二次同余式的二次剩余。根据欧拉判别条件，有 $C^{\frac{p - 1}{2}} \equiv 1 (\mod p)$ 和 $C^{\frac{p - 1}{2}} \equiv 1 (\mod q)$ 成立，同时得出当大素数 $p$ 满足 $p \equiv q \equiv 3 (\mod 4)$ 时，即存在 $p + 1 = 4 k_{1}$ ， $q + 1 = 4 k_{2}$ ， $k_{1} \in Z$ ， $k_{2} \in Z$ ，不难得到：

${(C^{\frac{p + 1}{4}})}^{2} = C^{\frac{p + 1}{2}} = (C^{\frac{p - 1}{2}}) \cdot C$

$(C^{\frac{p - 1}{2}}) \cdot C \equiv C (\mod p)$

${(C^{\frac{p + 1}{4}})}^{2} \equiv C (\mod p)$

二次同余式的根为：

$M = k p \pm C^{\frac{p + 1}{4}}, k \in Z$

同理：

$M = k q \pm C^{\frac{p + 1}{4}}, k \in Z$

由此得到解密后的多解明文，还需增加额外的相关条件进一步甄别。在数论理论中，求解二次同余式与分解大数 $n$ 是等价的。

2.2. 优势与安全性

2.2.1. 优势

加密运算过程简单而快速，能够产生很多密钥组给不同的加密者使用。

公钥加密算法能够有效保证其产生的密文具有统计独立、均匀分布的特点。只有知道密钥D的人才能够解密，连加密者自己也无法解密，人为因素将不影响公钥密码系统的安全性。

2.2.2. 安全性分析

破解公钥加密最彻底的办法就是对 $N$ 因数分解，找出 $P, Q$ 。寻找 $P$ 和 $Q$ 的唯一办法是穷举。这对运算能力是一次考验，其计算用时为指数关系，使得冯诺依曼结构下的计算机无法完成有效的破解。

3. 难解问题的数学基础

3.1. 随机数

随机数可以理解为随机产生的数字或序列，具有随机性与不可预测性两个显著的特征。

随机性由均匀分布和独立性两个具体的准则来描述。均匀分布是指序列中每个数的出现频率是近似相等的，符合最大熵。独立性为正要出现的数 $a_{i}$ 与此前已知的数 $a_{i - 1}, a_{i - 2}, \dots, a_{1}$ 之间对应的互信息 $I (a_{i}; a_{i - 1}, a_{i - 2}, \dots, a_{1}) = 0$ 。而不可预测性即后面生成的数不受前面生成数的影响。

3.1.1. 随机数的数学描述

设无限序列 $x \in 2^{ω}$ ，序列 $x$ 的密度定义描述为：

设 $D (x, n) = \frac{1}{n} \sum_{i < n} x_{i}$ ，则 $D (x, n)$ 为序列 $x$ 到第 $n$ 项的密度。如果 $D (x, n)$ 存在一个极限，则称 $\lim_{n} D (x, n)$ 为序列 $x$ 的极限密度。

严格条件下，无限序列的极限密度应当满足公式：

$\lim_{n} D (x, n) = 1 / 2$

由于实际操作中很难实现无限序列，在非严格条件下，通常需要满足的公式为：

$\lim_{n} D (x, n) \to 1 / 2$

3.1.2. 量子比特序列与真随机数

产生量子随机数方法很多，以下为通过单个粒子的量子比特产生随机数的方法：

设存在 $n$ 个量子比特，每一个都有形式 $| ψ 〉 = α | + x 〉 + β | - x 〉$ ，沿着方向 $x$ 去测量每个量子比特，结果是 $+ x$ 的概率是 ${‖ α ‖}^{2}$ ，是 $- x$ 的概率是 ${‖ β ‖}^{2}$ 。在测完 $n$ 个量子比特之后，出现 $n$ 个结果，由此形成随机数序列 $S = {s_{1}, s_{2}, \dots, s_{n} | s_{i} \in (+ x, - x)}$ 。由于量子噪声的存在，测量结果是一个概率出现的结果，测量之前并不能对结果预测。当 $α = β$ 时，测量结果为 $+ x$ 和 $- x$ 的概率都是 $50 %$ ， $+ x$ 和 $- x$ 以相同概率出现 [4] 。

由于经典噪声和测量仪器的影响，无法保证 $+ x$ 和 $- x$ 出现的概率都是 $50 %$ 。如果 $+ x$ 的概率为 $50 % + ε$ ， $- x$ 出现的概率为 $50 % - ε$ ，可采用John von Neumann算法进行处理。

同时读取两个比特，去掉为11和00的结果。对于10和01的结果只输出前一个比特。设 $+ x$ 为0、 $- x$ 为1，可得：

$11 \to (1 / 2 - ε) (1 / 2 - ε) = 1 / 4 - ε + ε^{2}$

$10 \to (1 / 2 - ε) (1 / 2 + ε) = 1 / 4 - ε^{2}$

$01 \to (1 / 2 + ε) (1 / 2 - ε) = 1 / 4 - ε^{2}$

$00 \to (1 / 2 + ε) (1 / 2 + ε) = 1 / 4 + ε + ε^{2}$

结果表明，考虑测量误差的前提下，得到比特1和比特0的概率是相等的。

结合John von Neumann算法和Bell态，每次从四个Bell态中随机选取一个，用Bell基来测量Bell态的两个粒子，得到11、10、01和00，最后使用John von Neumann算法可以获得出现概率相通的比特0和比特1，由此构成可靠的随机数序列。

3.2. 大数分解难解问题

3.2.1. 素数无穷的证明

通过假设即可反证出“素数为有限多个”的命题是伪命题。

3.2.2. 素性检验

构建大数分解难题的基础是进行大数的素性检验。RSA加密算法在实现过程中需要寻找两个足够大的质数，在数足够大的时候，如何确定它是一个素数，需要用到数论中关于素数(质数)的相关理论。

在Rabin密码体制、Okamoto签名体制和ElGamal签名体制中，同样需要使用大素数，同样需要素性检验的合理方式。

Miller-Rabin素性检验法

采用Miller-Rabin素性检验方法检验的大整数，如果已经进行了t步迭代，还没有出现非素数的判定结果，那么这个数是素数的概率不低于 $1 - 2^{- t}$ 。当t充分大的时候，通过此方法检测的数为素数的概率已经足够可靠。

费马素性检验

费马素性检验的本质就是借助费马小定理来判定选出的大整数是素数还是合数。其本质与Miller-Rabin素性检验类似。

Solovay-Stassen素性检验

对于一个大于2的素数n，由于 $x^{2} \equiv b (\mod n)$ ，其中的b是否为二次剩余可借助欧拉判别法或者勒让德符号进行判定。而如果采用雅可比符号判定，对整数b而言，计算 $b^{(n - 1) / 2} (\mod n)$ ，如果 $b^{(n - 1) / 2} \neq (\frac{b}{n}) (\mod n)$ ，就能够确定n一定不是素数。

确定性的素性检验方法

借助Eratosthenes筛选法，给出一个正数x，满足 $\lim_{x \to \infty} \sqrt[n]{x} = 1$ ，可以设计一种可行的确定性素性检验方法。

面对一个给定的大整数 $m$ ，要判定其是否为素数的时候。首先把问题进行转化，变成确定一个常数 $k \geq 1$ ，得到新的数 $M = m + k$ ，寻找比M小的素数的问题。此时，借助Eratosthenes筛选法，能够逐一得到一个比M小的素数，然后再进行判定，如果m存在于这些寻找到的素数中，则能够确定 $m$ 为素数。如此一来，不论结果如何，都能够一次性获得大整数m的确定性素性检验结果 [5] 。

这种类似于迭代的计算方式，巧妙地借助了平方根的运算。同时，借助整数的其他相关性质，此算法能够在计算机中有效实现，并且具备很高的素性检验速度。

3.3. 离散对数难解问题

3.3.1. 离散对数问题描述

在有限循环群G中，存在一个生成元a，对任意已知的整数n，容易得到 $a^{n} = b \in G$ 。但是在情况相反时，已知 $b \in G$ 和有限循环群的生成元a，借助 $a^{n} = b$ 计算出n是十分困难的，构成数学基础上的计算复杂性难解问题。

之所以逆向计算整数n十分困难，首先因为是有限循环群，它的阶式有限的，对应的同一个b，实际上可能有无数的解，设 $o r d (a) = m$ ，对应的解需要满足 $r \equiv n (\mod (o r d (a)))$ ，而如果要从这么多解中确定出某个值，自然是不可能。此外，如果并不知道相应循环群的阶m，求解n就更加困难了。

3.3.2. 离散对数问题在数字签名中的应用

密码专家们设计了ElGamal、Okamoto等具体的数字签名认证方法 [6] 。其全过程可以分为系统参数设置、签名产生过程和签名验证过程三个部分。

系统参数设置：

确定有限群换群的阶p。选取一个大素数p，则构成一个有限循环群 $G = p Z - {0}$ 。同时确定一个大素数q，可以是 $p - 1$ 的素因数，也可以就是 $p - 1$ 。

在 $G = p Z - {0}$ 中随机选出生成元g，要求 $g^{q} \equiv 1 (\mod p)$ 。

签名方生成其持有的私钥n，这个私钥可以被限制在一定范围内。同时生成公钥K，要求 $K = g^{n} (\mod p)$ 。

签名生成部分：

设置需要签名的消息为m，由签名方计算关于的杂凑值 $H (m)$ ，在 $(1, q)$ 中，由随机数 $k$ ，根据 $r \equiv g^{k} (\mod p)$ 求得 $r$ 。

根据签名方程 $a k \equiv (b + c s) (\mod q)$ 计算出对应的s值，其中方程的系数a，b，c与 $H (m)$ 之间存在着一定的关系，可以由签名方决定。由所得到的r值和s值，构建具体的签名 $(r, s)$ 。

签名验证部分：

接收方收到消息与签名 $(r, s)$ ，然后使用验证方程进行检验所收到的签名是否属实。一般情况下，判定是否满足 $r^{a} = g^{b} y^{c} (\mod p)$ 。

3.3.3. 前沿动态

在近期的研究中，基于多离散对数问题，出现了MDLP公钥加密等算法，是此类难解问题基础上加密算法的有效改进，但后来也被证明其算法应用是不严格安全的 [7] 。

3.4. K椭圆曲线上的离散对数难解问题

3.4.1. 椭圆曲线上的离散对数问题

椭圆曲线上的离散对数问题的本质就是把离散对数难解问题的数的问题放到由域上的Weierstrass方程所定义的椭圆等曲线上考虑，具体而言，就是在已经知道素数p和 $G F (p)$ 的椭圆曲线群 $E (G F (p)) = {(x, y) \in G F (p) {| y}^{2} = x^{3} + a x + b, a \in G F (p), b \in G F (p)} \cup {0}$ 以及点 $P = (x, y)$ 的阶是一个大素数的基础上，解决下面问题：

给定 $s \in N$ 的条件下，并且 $s < p$ ，以及 $P = (x, y)$ ，计算点 $s P = Q = (x_{s}, y_{s})$ 是比较容易的。而逆运算中，已知点Q的情况，由 $s P = Q = (x_{s}, y_{s})$ 求s的值是几乎不可能实现的。

3.4.2. 基于椭圆曲线离散对数问题的密码体制

目前已经成型的密码体制有Diffie-hellmen密钥交换和ElGamal密码体制，它们是椭圆曲线密码体制的典型系统。

Diffie-hellmen密钥交换过程

选择大素数 $p$ 并确定 $E (G F (p))$ ，选取 $E (G F (p))$ 的一个生成元 $G (x_{1}, y_{1})$ ，这个生成元应当是非常大的素数，所谓 $G (x_{1}, y_{1})$ 的阶梯，记作n， $E (G F (p))$ 和 $G (x_{1}, y_{1})$ 可以公开。

然后，事先通信双方密钥交换的过程：由甲选定一个小于n的整数 $n_{a}$ ，作为私钥，再根据 $P_{a} = n_{a} G (x_{1}, y_{1})$ 和 $P_{a} \in E (G F (p))$ 得到 $P_{a}$ ，并作为公钥。同样，乙也选定一个小于n的整数 $n_{b}$ ，作为私钥，并根据 $P_{b} = n_{b} G (x_{1}, y_{1})$ 和 $P_{b} \in E (G F (p))$ 求出 $P_{b}$ ，把 $P_{b}$ 也作为公钥。甲计算 $K_{1} = n_{a} P_{b}$ ， $P_{b} \in E (G F (p))$ ，乙计算 $K_{2} = n_{b} P_{a}$ ， $P_{a} \in E (G F (p))$ 。甲乙可以把 $K_{1}$ 和 $K_{2}$ 作为双方共同的私钥。

$K_{1} = n_{a} P_{b} = n_{a} (n_{b} G (x_{1}, y_{1})) = n_{b} (n_{a} G (x_{1}, y_{1})) = n_{b} P_{a} = K_{2}$

其中：

$P_{a} \in E (G F (p))$ ， $P_{b} \in E (G F (p))$

在不知道私钥 $n_{a}$ 的条件下，由 $P_{a} = n_{a} G (x_{1}, y_{1})$ 和 $P_{a} \in E (G F (p))$ 计算 $n_{a}$ ，就是椭圆曲线离散对数问题。同理，在不知道 $n_{b}$ 的情况下，由 $P_{b} = n_{b} G (x_{1}, y_{1})$ 和 $P_{b} \in E (G F (p))$ 计算 $n_{b}$ 也是椭圆曲线离散对数问题，由此保证了安全性。

ElGamal密码体系

选择一个大素数 $p$ 和两个小于该素数的随机数 $g$ 和 $x$ ，计算 $y \equiv g^{x} (\mod p)$ ，得出 $y$ 。然后以 $(y, g, p)$ 为公钥， $x$ 为私钥。若明文为 $M$ ，则相应的加密过程为选定一个满足 $(k, p - 1) = 1$ 的数 $k$ ，计算 $C_{1} = g^{k} (\mod p)$ 和 $C_{2} = y^{k} M (\mod p)$ ，得出密文 $C = (C_{1}, C_{2})$ 。

ElGamal算法的解密过程的核心是通过 $M \equiv \frac{C_{1}}{C_{2}} (\mod p)$ 得到明文，证明如下：

$\frac{C_{1}}{C_{2}^{x}} (\mod p) \equiv \frac{y^{k} M}{g^{k x}} (\mod p) \equiv \frac{y^{k} M}{{(g^{x})}^{k}} (\mod p) \equiv M (\mod p)$

在加密过程中的随机数 $k$ 是信息发送方生成的，接收方根据收到的密文，通过 $C_{1} = g^{k} (\mod p)$ 运算得到 $k$ ，然后进行解密运算，解密时要用到私钥 $x$ 。

首先需要选择一个椭圆曲线 $E (G F (p))$ ，并把明文与 $E (G F (p))$ 上面的点建立对应关系。其加密和解密过程也就转化为了在规定了 $\oplus$ 运算法则的Abel群中的运算，其具体过程分析如下：

首先，选取 $E (G F (p))$ 上的一个生成元 $G$ ，把 $E (G F (p))$ 和 $G$ 作为公开的参数。然后，接收方根据 $P_{b} = n_{b} G (x, y)$ 把 $P_{b}$ 作为公钥， $n_{b}$ 作为密钥。发送方选取一个正整数 $k$ ，同时根据公钥 $P_{b}$ 对明文 $P_{m}$ 进行运算：

$C_{m} = (C_{1}, C_{2}) = (k G (x, y), P_{m} + k P_{b})$

$C_{1} = k G (x, y)$

$C_{2} = P_{m} + k P_{b}$

解密的过程就是 $C_{2} - n_{b} C_{1}$ 的过程，因为：

$C_{2} - n_{b} C_{1} = P_{m} + k P_{b} - n_{b} k G (x, y) = P_{m} + k n_{b} G (x, y) - n_{b} k G (x, y) = P_{m}$

非法的窃听者由于没有私钥 $n_{b}$ ，也就不能解密。另外，如果要想根据 $C_{m}$ 得到 $P_{m}$ ，就必须知道整数 $k$ ，而要知道 $k$ ，就必须知道椭圆曲线 $E (G F (p))$ 上的点 $G$ 和 $k G$ ，这显然是椭圆曲线上的离散对数问题，安全性得到了保障。

分析展望

椭圆曲线上的密码体制具有安全性高的特点，同时，由于密钥量比较小，密码设计者能够发挥的空间比较大。此外，作为椭圆曲线的推广，已经出现了超椭圆曲线理论和超椭圆曲线上的离散对数难解问题为基础的密码体制HECC，构成了椭圆曲线密码体制ECC理论的发展方向 [8] 。

4. 抗量子安全

由于量子计算的并行特性是量子图灵机的内禀属性，经典计算中的难解问题可以通过量子计算化作可解问题。不过，从当前的情况来看，在量子计算中仍然存在难解问题。

当然，由于采用量子密钥分配的密码算法和采用Hash函数构建的单向函数签名算法的安全性来自量子物理特性和严格单向函数，不具备转化为求解广义离散傅里叶变换问题的条件，故不受量子计算的威胁 [9] 。不过上述算法本身有显著的应用局限使其难以取代优化计算复杂度的抗量子密码。

4.1. 计算复杂性与问题分类

一个要求给出解答的一般提问称作一个问题，记作 $π$ ，它通常由具体实例与询问两个部分组成。问题 $π$ 可以通过图灵机求解：

图灵机是一个三重组 $M = {\sum, ψ, δ}$ ，其中 $\sum = {\emptyset, 0, 1 \dots}$ 表示一个有限符号集， $\emptyset$ 为一个特殊的符号——空白； $ψ = {s, h}$ 表示机器状态的有限符集合，s和h分别表示初始态和最终态； $δ$ 为一个跃迁函数，满足：

$δ : ψ \times \sum \mapsto ψ \times \sum \times {- 1, 0, 1}$

通过图灵机求解问题 $π$ 时，时间 $T$ 和空间 $S$ 分别称为算法的时间复杂度和空间复杂度。假设 $n$ 是输入规模，则 $T$ 和 $S$ 可以表示为 $n$ 的函数： $T (n)$ 和 $S (n)$ 。由此可以将算法简单分为两类，多项式时间算法和指数时间算法。当算法的执行时间是 $T (n) = O (n^{t})$ 的时候( $t$ 为常量)，称算法为多项式时间算法或有效算法，反之亦然。通常把具有多项式时间的算法简称P问题，把找不到有效算法的问题称为难解问题。随着图灵机计算能力的大幅度提高，某些难解问题正渐渐转化为易解问题。当前，难解问题分NP问题、NPC问题(NP难题)、co-NP问题。

此外，从空间的角度定义的难解问题有PSPACE问题、NPSPACE问题、PSPACE-c问题等。PSPACE问题是指在多项式空间内可解的问题，包含NP问题和co-NP问题。

4.2. 子集和问题与OUT量子公钥密码算法

虽然量子计算机比电子计算机的计算能力和储存能力更强，能够将大整数因子分解、将离散对数等NP问题转化为QP问题。但是，子集和问题对量子图灵机来说依然是难解问题。

子集和问题描述：

给定 $n$ 个正整数 $a_{i} (i = 1, 2, \dots, n)$ 以及正整数 $S$ ，求方程

$a_{1} x_{1} + a_{2} x_{2} + \dots + a_{n} x_{n} = S$

是否有满足 $x_{i} \in {0, 1} (i = 1, 2, \dots, n)$ 的解。

日本NTT实验室的密码专家T. Okamoto、K. Tanaka和S. Uchiyama基于环上的子集和问题提出了量子公钥密码算法，这里简称OUT算法。

下面介绍该算法的密钥产生过程和加密方式。

4.2.1. 密钥产生

1) 确定适合系统的固定数域集和K，随机选取K中的一个数域 $K$ ， $O_{k}$ 为 $K$ 上的整数环， $Z$ 为 $K$ 上的有理数环参数 $n, k \in Q$ 。

2) 选取整数环 $O_{k}$ 的质理想 $ρ$ ，并随机选取 $O_{k}$ 中的元素 $g$ 使其为有限域 $O_{k} / ρ$ 上乘法的生成子。其中， $O_{k} / ρ$ 中的元素可以用基 ${1, ω_{2}, \dots, ω_{l}}$ 唯一地表示，即对于任意的整数 $x \in O_{k}$ ，都存有有理整数 $x_{1}, x_{2}, \dots, x_{l} \in Q$ $(0 \leq x_{i} \leq e_{i})$ ，使得

$x = x_{1} + x_{2} ω_{2} + \dots + x_{l} ω_{l} (\mod p)$

3) 选 $n$ 取个整数 $p_{1}, p_{2}, \dots, p_{n} \in O_{k} / ρ$ ，满足： $N (p_{i}) (i = 1, 2, \dots, n)$ 为联合质数(co-prime)。对于整数集合 ${p_{1}, p_{2}, \dots, p_{n}}$ 中的任意子集 ${p_{i_{1}}, p_{i_{2}}, \dots, p_{i_{k}},}$ ，都存在有理数 $a_{1}, a_{2}, \dots, a_{l} (0 \leq a_{i} < e_{i})$ ，使得：

$\prod_{j = 1}^{k} p_{i_{j}} = a_{1} + a_{2} ω_{2} + \dots + a_{l} ω_{l}$

4) 利用Shor算法求解离散对数问题，得到 $a_{1}, a_{2}, \dots, a_{n}$ ，使得

$p_{i} \equiv g^{a_{i}} (\mod p)$

式子中 $b_{i} \in Q / (N (ρ) - 1) Z$ 。

5) 随机选取有理整数 $d \in Z / (N (ρ) - 1) Z$ 。

6) 计算 $b_{i} = a_{i} + d \mod (N (ρ) - 1) (i = 1, 2, \dots, n)$ 。

7) 公钥为 ${K, n, k, b_{1}, b_{2}, \dots, b_{i}}$ ，私钥为 ${K, g, d, p, p_{1}, p_{2}, \dots, p_{n}}$ 。记 $K_{p}$ 和 $K_{s}$ 分别为公钥和私钥，则有：

$K_{p} = {K, n, k, b_{1}, b_{2}, \dots, b_{i}}$

$K_{s} = {K, g, d, p, p_{1}, p_{2}, \dots, p_{n}}$

4.2.2. 加密过程

1) 固定明文 $M$ 的长度为 $[\log_{2} (\begin{matrix} n \\ k \end{matrix})]$ 。

2) 将明文按照下列方式编码为二进制串 $m = (m_{1}, m_{2}, \dots, m_{n})$ ， $m$ 的Hamming权重为设置为 $l : l \leftarrow k$ 。对于 $i$ 循环执行下面的过程 $(1 \leq i \leq n)$ ：如果 $m \geq (\begin{matrix} n - i \\ l \end{matrix})$ ， $M \leftarrow M - (\begin{matrix} n - i \\ l \end{matrix})$ ， $l \leftarrow l - 1$ ；否则 $m_{i} \leftarrow 0$ 。其中 $l \geq 0$ 时， $(\begin{matrix} l \\ 0 \end{matrix}) = 1$ 。

3) 计算密文

$c = \sum_{i = 1}^{n} m_{i} b_{i}$

4.2.3. 解密过程

1) 计算 $r = c - k d \mod (N (ρ) - 1)$ 。

2) 计算 $u \equiv g^{r} (\mod p)$ 。

3) 如果 $p_{i} | u, m_{i} \leftarrow 1$ ，否则 $m_{i} \leftarrow 0$ 。对所有的 $p_{i}$ 的计算都完成后，设 $m = (m_{1}, m_{2}, \dots, m_{n})$ 。

4) 按下面过程将 $m$ 解码为明文。

a) $m \leftarrow 0, l \leftarrow k$ 。

b) 对于 $i$ 循环这个过程 $(1 \leq i \leq n)$ ：如果 $m_{i} = 1$ ， $M \leftarrow M + (\begin{matrix} n - i \\ l \end{matrix})$ ， $l \leftarrow l - 1$ 。

4.2.4. 安全性分析

本质上，OUT算法建立在背包体制上，其安全性又是基于图灵机的，即能够抵御具有量子计算能力的攻击 [10] 。OUT密码算法是一个具有量子计算复杂度的公钥密码算法，即量子计算机并不能破解所有的公钥加密算法。

4.3. 最短格矢问题与NTRU公钥密码算法

NTRU算法是一种有效的公钥密码算法，已经被IEEE P1316工作组定为标准，其算法安全性的核心就是最短格矢问题(SVP) [11] 。在一定条件下，最短格矢问题是NPC问题，NTRU算法被认为是安全的。

最短矢格问题是指：

给定维正整数域上的格矢(lattice，子群)

$L = {\sum_{i = 1}^{n} a_{i} b_{i} | a_{i} \in Z, \leq i \leq n}$

其中格基为 $B = {b_{1}, b_{2}, \dots, b_{n}} \subset Z^{n}$ ，寻找一个非零格矢 $v \in L$ 使 $‖ v ‖ \leq a λ$ 。

最短格矢问题是一个NP问题，可以用 $L^{3}$ 算法求解最短矢格问题，该算法中 $a = 2^{(n - 1) / 2}$ ，其时间复杂度为 $O (n^{4} \log_{2} ξ)$ ，其中实数 $ξ \geq 2$ 满足 ${‖ b_{i} ‖}^{2} \leq ξ (1 \leq i \leq n)$ [12] 。

由于最短格矢问题是一个搜索问题，那么就可以用Grove搜索算法求解。与Koy的原始对偶方法所需的时间 $T_{k}$ 相比，量子搜索算法的运行时间大约为Koy方法的8次方根，也就是

$T_{Q} = T_{K}^{1 / 8}$

有一个实验采用了Shoup NTL图书馆的400 MHz PC机以BKZ方法求解，计算用时情况为

$T_{B K Z} \geq 10^{0.109 5 N - 12.640 2} M I P S - y e a l s$

由此可以估计出采用量子搜索算法求解最短格矢问题的执行时间为

$T_{Q} \geq 10^{(0.109 5 N - 12.640 2) / 8} M I P S - y e a l s$

几种情况下的运算用时对比如表1所示。

可见，借助量子搜索算法确实使求解最短格矢问题的计算用时急剧减少，但其绝对时间仍然很长。对于量子图灵机来说，求解最短格矢问题的时间复杂度依然满足指数关系 [13] 。即量子搜索算法也不能完全解决最短格矢问题。

5. 结语

从最初的RSA密码、Rabin加密算法到后来的Diffie-hellmen密钥交换和ElGamal密码体系，再到具备抗量子攻击能力的OUT量子公钥密码算法和NTRU公钥密码算法，数学难解问题一直是公钥密码体系的安全核心。

Table 1. Computation time comparison

表1. 计算用时对比

从大数分解难解问题到离散对数难解问题、椭圆曲线上的离散对数难解问题乃至超椭圆曲线上的难解问题，到后来被证明量子计算也无法有效破解的子集和问题、最短格矢问题，对这些难解问题背后的数学基础的研究也一直是推进公钥密码算法不断改进的重要研究方向 [14] 。此外，具备抗量子特性的生物DNA密码、量子密码、量子通信的研究与应用必然建立在数学、物理学乃至生物学基础理论的突破性进展之上，显然这是一个漫长的过程。

与此同时，基于能够在量子图灵机的攻击下依旧保持指数时间/空间计算复杂度——子集和问题、最短格矢问题、PSPACE问题、NPSPACE问题、PSPACE-c问题等——的难解问题，致力于通信安全的密码学家们也推出了OUT量子公钥密码算法和NTRU公钥密码算法等抗量子攻击加密算法，不断增强公钥密码的抗量子安全性，从而为量子密码等新型密码体制的进一步发展提供了时间条件。

基金项目

国家自然科学基金项目(U1204602)，数学工程与先进计算国家重点实验室开放课题项目(2013A14)。

文章引用

唐彪高泽,黄婉泽,赵洪安,胡勇战,闫争争,李宏欣. 公钥加密算法与抗量子密码体制安全性的数学分析
Mathematical Analysis of Public Key Encryption Algorithm and Security of Anti Quantum Cryptography[J]. 应用数学进展, 2018, 07(10): 1263-1274. https://doi.org/10.12677/AAM.2018.710147

参考文献

1. 曾贵华. 量子密码学[M]. 北京: 科学出版社, 2006: 6-9.

2. 梅挺. 网络信息安全原理[M]. 北京: 科学出版社, 2009: 20-72.

3. 祝跃飞, 张亚娟. 公钥密码学设计原理与可证安全[M]. 北京: 高等教育出版社, 2010: 22-54.

4. 马瑞霖. 量子密码通信[M]. 北京: 科学出版社, 2006: 33-61.

5. 张焕炯. 加密与认证技术的数学基础[M]. 北京: 国防工业出版社, 2013: 95-103.

6. Loepp, S. and Wootters, W.K. (2008) Protecting Information: From Classical Error Correction to Quantum Cryptography. Cambridge University Press, Cambridge, 163-207.

7. 苏盛辉, 孙国栋. 基于多离散对数问题的公钥密码的分析[J]. 电子学报, 2018, 46(1): 218-222.

8. 张焕国, 王后珍. 抗量子计算密码体制研究(待续) [J]. 信息网络安全, 2011(5): 1-4.

9. 张焕国, 王后珍. 抗量子计算密码体制研究(续前) [J]. 信息网络安全, 2011(6): 56-59.

10. 费向东, 潘芳, 潘郁. 背包公钥密码安全新方案[J]. 计算机应用研究, 2018(1).

11. 吴艳华. 基于GRSA和NTRU的部分同态加密方案的研究[D]: [硕士学位论文]. 昆明: 云南大学, 2015.

12. 李子臣, 张卷美, 杨亚涛, 等. 基于NTRU的全同态加密方案[J]. 电子学报, 2018, 46(4): 938-944.

13. 刘文瑞. 抗量子计算攻击密码体制发展分析[J]. 通信技术, 2017, 50(5): 1054-1059.

14. Benenti, G., Casati, G. and Strini, G. (2004) Principles of Quantum Computation and Information I. World Scientific Publishing, Italy, 146-166. https://doi.org/10.1142/5528

NOTES

^*通讯作者。

期刊菜单