一些奇异同谱图的性质研究 Research on the Property of Some Singularly Cospectral Graphs

doi:10.12677/ORF.2023.132124

Operations Research and Fuzziology
Vol. 13 No. 02 ( 2023 ), Article ID: 64613 , 7 pages
10.12677/ORF.2023.132124

一些奇异同谱图的性质研究

梁超凡，姜艺淼

●How to Cite this Article

长安大学理学院，陕西西安

收稿日期：2023年3月14日；录用日期：2023年4月19日；发布日期：2023年4月27日

摘要

图G的能量 $E (G)$ 是其邻接矩阵的所有特征值绝对值的和。如果两个图有相同的非零奇异值及重数，那么被称为奇异同谱图。奇异同谱图的刻画及性质研究对于图能量问题的推进有重要意义。本文利用克罗内克积和笛卡尔积运算，给出了一些新的关于奇异同谱图的性质。

关键词

图能量，奇异同谱图，克罗内克积，笛卡尔积

Research on the Property of Some Singularly Cospectral Graphs

Chaofan Liang, Yimiao Jiang

School of Science, Chang’an University, Xi’an Shaanxi

Received: Mar. 14^th, 2023; accepted: Apr. 19^th, 2023; published: Apr. 27^th, 2023

ABSTRACT

The energy $E (G)$ of graph G is the sum of the absolute values of all the eigenvalues of its adjacency matrix. If two graphs have the same non-zero singular values with the same multiplicities, then they are called singularly cospectral. The study of the characterization and properties of singularly cospectral graphs is important for the advancement of the graph energy problem. In this paper, some new properties on singularly cospectral graphs are given using the Kronecker product and the Cartesian product.

Keywords:Graph Energy, Singularly Cospectral Graph, Kronecker Product, Cartesian Product

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

设无向简单图G的顶点集为 $V (G) = {v_{1}, v_{2}, \dots, v_{n}}$ ，边集为 $E (G)$ 。其邻接矩阵定义为 $A (G) = (a_{i j})$ ，其中 $a_{i j} = {\begin{cases} 1, 如果 v_{i} \sim v_{j}, \\ 0, 其它 . \end{cases}$ 。图G的特征值就是邻接矩阵 $A (G)$ 的特征值。图G的谱定义为 $A (G)$ 的特征值的多重集，记为 $Spec (G)$ 。假设 $A (G)$ 的不同特征值为 $λ_{1} > λ_{2} > \dots > λ_{s}$ ，其重数分别为 $m_{1}, m_{2}, \dots, m_{s}$ ，则G的谱记为 $Spec (G) = (\begin{matrix} λ_{1} & λ_{2} & \dots & λ_{s} \\ m_{1} & m_{2} & \dots & m_{s} \end{matrix})$ 。若图G的顶点集可划分为两个非空子集X和Y，使得G的任一条边都有一个端点在X中，另一个端点在Y中，则称G为二部图。图能量的研究起源于有机化学，1978年Gutman [1] 首先将图G的能量 $E (G)$ 定义为图G的特征值的绝对值之和，即 $E (G) = \sum_{i = 1}^{s} m_{i} | λ_{i} |$ 。如果 $E (G) = E (H)$ ，则称两个不同构的图G和图H等能量。如果两个图具有相同的谱，则称它们是同谱的。

为了进一步研究图的能量，Nikiforov [2] 引入了奇异同谱的定义。如果两个图具有相同的非零奇异值及重数，则称这两个图是奇异同谱的。显然同谱一定奇异同谱，反之不然。奇异同谱图的非零特征值的绝对值是相同。因此，奇异同谱图自然是等能量的。Nikiforov [2] 提出了寻找两个图是奇异同谱的充要条件的问题。与被充分研究的同谱图不同(研究结果可以参考文献 [3] [4] [5] [6] [7] )，很少有文献关注到奇异同谱图。Conde等人 [8] 通过给出奇异同谱的一些等价条件，在一定程度上回答了Nikiforov的问题。此外，他们还提出了一个寻找非同谱的奇异同谱图的问题。本文利用克罗内克积和笛卡尔积运算，给出了一些新的关于奇异同谱图的性质。

2. 预备知识

定义2.1给出了克罗内克积的矩阵表示。

定义2.1 [9] 设 $A = (a_{i j})$ 是 $(m \times n)$ 的矩阵， $B = (b_{i j})$ 是 $(r \times s)$ 的矩阵。矩阵A和B的克罗内克积(张量积)，记为 $A \otimes B$ ，被定义为分块矩阵

$A \otimes B = (\begin{matrix} a_{11} B & a_{12} B & \dots & a_{1 n} B \\ a_{21} B & a_{22} B & \dots & a_{2 n} B \\ ⋮ & ⋮ & ⋮ \\ a_{m 1} B & a_{m 2} B & \dots & a_{m n} B \end{matrix}) .$

$A \otimes B$ 的阶数为 $(m r \times n s)$ ，有mn个块，且第 $(i, j)$ 个块是 $(r \times s)$ 阶矩阵 $a_{i j} B$ 。

定义2.2给出了两个图的笛卡尔积的定义方式。

定义2.2 [10] 两个图 $G_{1}$ 和 $G_{2}$ 的笛卡尔积 $G_{1} □ G_{2}$ 的顶点集为 $V (G_{1}) \times V (G_{2})$ ，如果在 $G_{1}$ 中 $u_{1}$ 和 $v_{1}$ 相邻且 $u_{2} = v_{2}$ ，或者 $u_{1} = v_{1}$ 且在 $G_{2}$ 中 $u_{2}$ 和 $v_{2}$ 相邻，那么顶点 $(u_{1}, u_{2})$ 和 $(v_{1}, v_{2})$ 是相邻的。

定理2.1给出了矩阵克罗内克积、笛卡尔积的谱刻画和特征向量的对应关系。

定理2.1 [10] 设A是m阶方阵，B是n阶方阵。假设 $λ_{i} (1 \leq i \leq m)$ 是A的任意特征值，对应的特征向量为 $x_{i}$ ， $μ_{j} (1 \leq j \leq n)$ 是B的任意特征值，对应的特征向量为 $y_{j}$ 。那么 $A \otimes B$ 和 $A □ B$ 的谱和特征向量如下：

i) $λ_{i} μ_{j} (1 \leq i \leq m, 1 \leq j \leq n)$ 是 $A \otimes B$ 的一个特征值，对应的特征向量为 $x_{i} \otimes y_{j}$ 。

ii) $λ_{i} + μ_{j} (1 \leq i \leq m, 1 \leq j \leq n)$ 是 $A □ B$ 的一个特征值，对应的特征向量为 $x_{i} \otimes y_{j}$ 。

3. 一些奇异同谱图的性质

下面我们利用图的克罗内克积和笛卡尔积，给出一些新的奇异同谱图的性质。

定理3.1设 $G_{1}$ 和 $G_{2}$ 是一对n阶奇异同谱图。设 $H_{1}$ 和 $H_{2}$ 是一对m阶同谱图。

i) 如果 $H_{1}$ 和 $H_{2}$ 是二部图，那么 $A (G_{1}) \otimes A (H_{1})$ 和 $A (G_{2}) \otimes A (H_{2})$ 是同谱的。

ii) 如果 $H_{1}$ 和 $H_{2}$ 是二部图，那么 $A (G_{1}) □ A (H_{1})$ 和 $A (G_{2}) □ A (H_{2})$ 是奇异同谱的。

iii) 如果 $H_{1}$ 和 $H_{2}$ 不是二部图，那么 $A (G_{1}) \otimes A (H_{1})$ 和 $A (G_{2}) \otimes A (H_{2})$ 是奇异同谱的。

证明：i) 假设图 $G_{1}$ 和 $G_{2}$ 的特征值分别按 $| λ_{1} | \geq | λ_{2} | \geq \dots \geq | λ_{n} |$ ； $| μ_{1} | \geq | μ_{2} | \geq \dots \geq | μ_{n} |$ 排列。因为图 $G_{1}$ 和 $G_{2}$ 是奇异同谱的，我们有 $| λ_{i} | = | μ_{i} |$ 。由于 $H_{i} (i = 1, 2)$ 是一个二部图，那么 $ν_{j}$ 是 $H_{i}$ 的特征值当且仅当 $- ν_{j}$ 也是 $H_{i}$ 的特征值。根据定理2.1，我们有

$\begin{array}{l} Spec (A (G_{1}) \otimes A (H_{1})) = {\pm λ_{i} ν_{j} | i = 1, \dots, n, j = 1, \dots, ⌈ \frac{m}{2} ⌉}, \\ Spec (A (G_{2}) \otimes A (H_{2})) = {\pm μ_{i} ν_{j} | i = 1, \dots, n, j = 1, \dots, ⌈ \frac{m}{2} ⌉} . \end{array}$ (1)

由此可见， $A (G_{1}) \otimes A (H_{1})$ 和 $A (G_{2}) \otimes A (H_{2})$ 是同谱的。

ii) 根据定理2.1，我们有

$\begin{array}{l} Spec (A (G_{1}) □ A (H_{1})) = {λ_{i} \pm ν_{j} | i = 1, \dots, n, j = 1, \dots, ⌈ \frac{m}{2} ⌉}, \\ Spec (A (G_{2}) □ A (H_{2})) = {μ_{i} \pm ν_{j} | i = 1, \dots, n, j = 1, \dots, ⌈ \frac{m}{2} ⌉} . \end{array}$ (2)

如果 $λ_{i} = μ_{i}$ ，则 $λ_{i} \pm ν_{j} = μ_{i} \pm ν_{j} (i = 1, \dots, n; j = 1, \dots, ⌈ \frac{m}{2} ⌉)$ ，否则 $λ_{i} = - μ_{i}$ ，有 $λ_{i} \pm ν_{j} = - (μ_{i} \mp ν_{j})$ 。由此可知， $| λ_{i} \pm ν_{j} | = | μ_{i} \pm ν_{j} |$ ，即 $A (G_{1}) □ A (H_{1})$ 和 $A (G_{2}) □ A (H_{2})$ 是奇异同谱的。

iii) 由于 $H_{i} (i = 1, 2)$ 不是一个二部图，因此存在 $H_{i}$ 的特征值 $ν_{j_{0}}$ ，使得 $- ν_{j_{0}}$ 不是 $H_{i}$ 的特征值。又因为图 $G_{1}$ 和 $G_{2}$ 是奇异同谱的，对于每个 $i = 1, \dots, n; j = 1, \dots, ⌈ \frac{m}{2} ⌉$ ，都有 $| λ_{i} ν_{j} | = | μ_{i} ν_{j} |$ 成立。由于图 $G_{1}$ 和 $G_{2}$ 是不同谱的，因此至少存在一个下标 $i_{0}$ ，使得 $λ_{i_{0}} = - μ_{i_{0}}$ ，因此存在特征值 $λ_{i_{0}} ν_{j_{0}}$ 不在 $A (G_{2}) \otimes A (H_{2})$ 的谱中，即 $λ_{i_{0}} ν_{j_{0}} \in Spec (A (G_{2}) \otimes A (H_{2}))$ 。这就意味着， $A (G_{1}) \otimes A (H_{1})$ 和 $A (G_{2}) \otimes A (H_{2})$ 是奇异同谱的。

如果 $H_{1}$ 和 $H_{2}$ 是同构图，那么我们可以立即得到一个推论。

推论3.2设 $G_{1}$ 和 $G_{2}$ 是一对n阶奇异同谱图。设H是一个m阶的图。

i) 如果H是一个二部图，那么 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 是同谱的。

ii) 如果H是一个二部图，那么 $A (G_{1}) □ A (H)$ 和 $A (G_{2}) □ A (H)$ 是奇异同谱的。

iii) 如果H不是一个二部图，那么 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 是奇异同谱的。

为了说明推论3.2，我们给出以下三个例子。

例3.3设 $G_{1}$ 和 $G_{2}$ 是一对奇异同谱图(见图1)，设H是4个顶点的路图(见图2)。我们可以得到 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 所对应的邻接矩阵图(见图3)。在表1中我们列出 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 的所有特征值，容易验证 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 是同谱的。

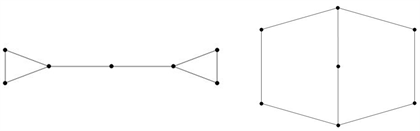
Figure 1. A pair of singularly cospectral graph $G_{1}$ and $G_{2}$

图1. 一对奇异同谱图 $G_{1}$ 与 $G_{2}$

Figure 2. Graph H

图2. 图H

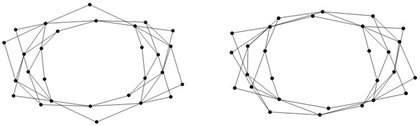
Figure 3. The adjacency matrix graph corresponding to $A (G_{1}) \otimes A (H)$ and $A (G_{2}) \otimes A ( H )$

图3. $A (G_{1}) \otimes A (H)$ 与 $A (G_{2}) \otimes A (H)$ 所对应的邻接矩阵图

Table 1. Eigenvalues of A ( G 1 ) ⊗ A ( H ) and A ( G 2 ) ⊗ A ( H )

表1. $A (G_{1}) \otimes A (H)$ 与 $A (G_{2}) \otimes A (H)$ 的特征值

例3.4设 $G_{1}$ 和 $G_{2}$ 是一对奇异同谱图(见图4)，设H是4个顶点的路图(见图5)。我们可以得到 $A (G_{1}) □ A (H)$ 和 $A (G_{2}) □ A (H)$ 所对应的邻接矩阵图(见图6)。在表2中我们列出 $A (G_{1}) □ A (H)$ 和 $A (G_{2}) □ A (H)$ 的所有特征值，容易验证 $A (G_{1}) □ A (H)$ 和 $A (G_{2}) □ A (H)$ 是奇异同谱的。

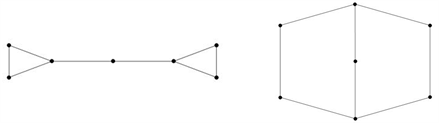
Figure 4. A pair of singularly cospectral graph $G_{1}$ and $G_{2}$

图4. 一对奇异同谱图 $G_{1}$ 与 $G_{2}$

Figure 5. Graph H

图5. 图H

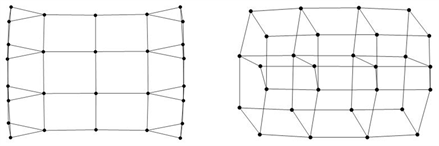
Figure 6. The adjacency matrix graph corresponding to $A (G_{1}) □ A (H)$ and $A (G_{2}) □ A ( H )$

图6. $A (G_{1}) □ A (H)$ 与 $A (G_{2}) □ A (H)$ 所对应的邻接矩阵图

Table 2. Eigenvalues of A ( G 1 ) □ A ( H ) and A ( G 2 ) □ A ( H )

表2. $A (G_{1}) □ A (H)$ 与 $A (G_{2}) □ A (H)$ 的特征值

例3.5设 $G_{1}$ 和 $G_{2}$ 是一对奇异同谱图(见图7)，设H是一个5个顶点的图(见图8)。我们可以得到 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 所对应的邻接矩阵图(见图9)。在表3中我们列出 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 的所有特征值，容易验证 $A (G_{1}) \otimes A (H)$ 和 $A (G_{2}) \otimes A (H)$ 是奇异同谱的。

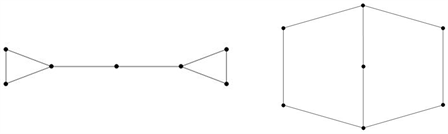
Figure 7. A pair of singularly cospectral graph $G_{1}$ and $G_{2}$

图7. 一对奇异同谱图 $G_{1}$ 与 $G_{2}$

Figure 8. Graph H

图8. 图H

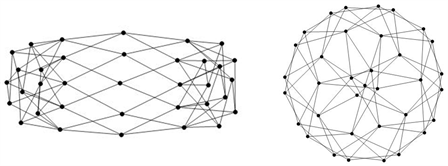
Figure 9. The adjacency matrix graph corresponding to $A (G_{1}) \otimes A (H)$ and $A (G_{2}) \otimes A ( H )$

图9. $A (G_{1}) \otimes A (H)$ 与 $A (G_{2}) \otimes A (H)$ 所对应的邻接矩阵图

Table 3. Eigenvalues of A ( G 1 ) ⊗ A ( H ) and A ( G 2 ) ⊗ A ( H )

表3. $A (G_{1}) \otimes A (H)$ 与 $A (G_{2}) \otimes A (H)$ 的特征值

4. 结语

奇异同谱图的刻画及性质研究对于图能量问题的推进具有重要意义，我们利用图的克罗内克积和笛卡尔积，给出一些新的奇异同谱图的性质，并给出了具体的实例。后续将利用此性质，研究构造同构图的充分条件。

文章引用

梁超凡,姜艺淼. 一些奇异同谱图的性质研究
Research on the Property of Some Singularly Cospectral Graphs[J]. 运筹与模糊学, 2023, 13(02): 1211-1217. https://doi.org/10.12677/ORF.2023.132124

参考文献

1. Gutman, I. (1978) The Energy of a Graph. Graz Forschungszentrum Mathematisch Statistische Sektion Berichte, 103, 1-22.

2. Nikiforov, V. (2016) Beyond Graph Energy: Norms of Graphs and Matrices. Linear Algebra and Its Applications, 506, 82-138. https://doi.org/10.1016/j.laa.2016.05.011

3. Abiad, A. and Alfaro, C.A. (2021) Enumeration of Cospectral and Coinvariant Graphs. Applied Mathematics and Computation, 408, Article ID: 126348. https://doi.org/10.1016/j.amc.2021.126348

4. Godsil, C.D. and Mckay, B.D. (1982) Constructing Cospectral Graphs. Aequationes Mathematicae, 25, 257-268. https://doi.org/10.1007/BF02189621

5. Ji, Y., Gong, S. and Wang, W. (2020) Constructing Cospectral Bi-partite Graphs. Discrete Mathematics, 343, Article ID: 112020. https://doi.org/10.1016/j.disc.2020.112020

6. Kannan, M.R., Pragada, S. and Wankhede, H. (2022) On the Construction of Cospectral Nonisomorphic Bipartite Graphs. Discrete Mathematics, 345, Article ID: 112916. https://doi.org/10.1016/j.disc.2022.112916

7. Qiu, L., Ji, Y. and Wang, W. (2020) On a Theorem of Godsil and McKay Concerning the Construction of Cospectral Graphs. Linear Algebra and Its Applications, 603, 265-274. https://doi.org/10.1016/j.laa.2020.05.025

8. Conde, C., Dratman, E. and Grippo, L.N. (2022) Finding Sin-gularly Cospectral Graphs. Linear and Multilinear Algebra, 71, 496-512. https://doi.org/10.1080/03081087.2022.2035306

9. Graham, A. (2018) Kronecker Products and Matrix Calculus with Applications. Courier Dover Publications, Chichester.

10. Cvetković, D.M., Rowlinson, P. and Simić, S. (2010) An Introduction to the Theory of Graph Spectra. Cambridge University Press, Cambridge.

期刊菜单