Pure Mathematics
Vol.07 No.03(2017), Article ID:20567,7
pages
10.12677/PM.2017.73024
A Note on the Automorphism Groups of Regular Polyhedrons
Lu Yu, Qi Cai
School of Mathematics, Yunnan Normal University Yunnan, Kunming Yunnan

Received: Apr. 30th, 2017; accepted: May 15th, 2017; published: May 19th, 2017

ABSTRACT
In this paper, by using the elementary method of permutation group theory, we give a simple characterization of the full automorphism groups of regular polyhedrons.
Keywords:Regular Polyhedron, Permutation Groups, Full Automorphism Groups
正多面体自同构群的一点注记
余露,蔡琦
云南师范大学数学学院,云南 昆明
收稿日期:2017年4月30日;录用日期:2017年5月15日;发布日期:2017年5月19日

摘 要
本文我们利用置换群理论的初等方法给出正多面体全自同构群的一个简单刻画。
关键词 :正多面体,置换群,全自同构群

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
正多面体(regular polyhedron),是指各个面都是全等的正多边形,并且每个二面角都相等的正多边形,早在欧几里得的《几何原本》中就已给出凸正多面体的全体分类,这类正多面体又称柏拉图多面体。之后科学家们又相继提出阿基米德多面体、开普勒多面体以及戈德堡多面体,其中星形多面体又属开普勒多面体。这些多面体的发现,对自然科学特别是几何学和组合数学的发展起到一定的推进作用。
目前已经知道正多面体共9种,其中凸正多面体有5种(如图1):正四面体、正六面体、正八面体、正十二面体以及正二十面体;星形多面体有4种(如图2):小星形十二面体、大星形十二面体、大十二面体以及大二十面体。
正多面体每个面都是全等的正多边形,具有高度对称性,在对这些正多边形的学习研究过程中可以发现,通过对这类正多面体作对称变换(旋转、反射)之后,依旧可以得到原先的正多面体,则称这类不改变几何体性质的变换为正多面体的自同构变换。正多面体的全体自同构变换在变换合成下显然成为一个群,这个群被称为这个正多面体的全体自同构群 [1] 。确定具有高对称性的几何体或者组合体的全体自同构群历来是代数和组合数学中的核心问题。
近年来,也有一些学者对多面体的相关性质作进一步刻画,McMullen在文献 [2] 中将三维正多面体推广到四维正多面体。Cunningham在文献 [3] 中根据自同构群完全分类出紧正则多面体。Itoh在文献 [4] 中通过识别等距凸多边形的边缘获得二维多面指标复合物,并专注于测地线度量空间的几何方面,最终确定它们的表面都是由柏拉图多面体组成:p-十二面体,p-二十面体,一个 覆盖正则
覆盖正则 边形(其中
边形(其中 )或一个完整的三角形。
)或一个完整的三角形。
有关三维空间中物体刚性变换(平移、旋转)所成运动群的研究,张远达 [5] 做了充分的描述,三维空间中稳定一点的刚性变换是旋转变换,而这样的旋转变换共有五类:它们分别是循环群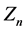 ,二面体群
,二面体群 ,正四面体群
,正四面体群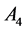 ,正六面体(正八面体)群
,正六面体(正八面体)群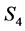 以及正十二面体(正二十面体)群
以及正十二面体(正二十面体)群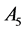 。
。

Figure 1. The convex polyhedras
图1. 凸正多面体

Figure 2. The Kepler-Poinsot polyhedra
图2. 星形正多面体
本文采用置换群理论的初等方法对上述9个正多面体的自同构群进行刻画,再次得到他们的全自同构群为:正四面体: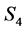 ;正六面体:
;正六面体: ;正八面体:
;正八面体: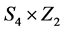 ;正十二面体:
;正十二面体: ;正二十面体:
;正二十面体: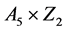 。星形多面体的自同构群皆为
。星形多面体的自同构群皆为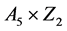 。
。
2. 预备知识
本节我们首先给出相关的一些基础知识和初等结果。下面首先给出正多面体对称变换的定义:
对称变换:在不改变图形形状和大小的前提下,经旋转或反射得到与自身重叠的几何体的变换,称为对称变换。
为便于讨论,称正多面体中有公共边的两个面互为相邻面,有公共顶点且在同一面上的两条边互为邻边,在同一条边的两个顶点互为相邻顶点,距离最远的对角线称为正多面体的主对角线。
定义:设非空集合 ,对于群
,对于群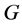 ,定义同态
,定义同态 使得
使得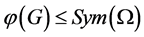 ,此时称群
,此时称群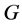 是
是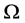 上的作用。一般地,为便于描述,下文均默认
上的作用。一般地,为便于描述,下文均默认 。对于
。对于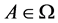 ,称
,称
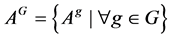
为 在
在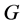 作用下产生的轨道,如果
作用下产生的轨道,如果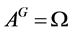 ,则称
,则称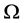 在
在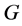 的作用下传递。称
的作用下传递。称

为点 的稳定子群。
的稳定子群。
显然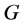 与稳定子群的关系有:
与稳定子群的关系有:
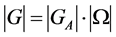
为便于讨论,称正多面体中有公共边的两个面互为相邻面,有公共顶点且在同一面上的两条边互为邻边,在同一条边的两个顶点互为相邻顶点,距离最远的对角线称为正多面体的主对角线。
由于正多面体的自同构群是保持自身不动的对称变换的全体,由定义知满足如下性质:
性质一 正多面体的任意两个相邻面对称变换前后依旧是相邻面。
性质二 正多面体(或正多边形)的任一组邻边对称变换前后依旧是邻边。
性质三 正多面体(或正多边形)相邻的顶点在对称变换前后依旧相邻。
性质四 正多面体的主对角线在对称变换前后依旧是主对角线。
根据上述性质,给出如下几个基本引理:
引理1. 固定正多边形的两个相邻顶点, 这样的对称变换是唯一的。
证明:对正多边形的顶点依次进行编号, ,其中
,其中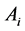 与
与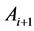 相邻,
相邻,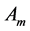 与
与 相邻
相邻 。
。
假设对称变换 固定前
固定前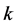 个顶点
个顶点 ,则
,则 的相邻顶点分别为
的相邻顶点分别为 ,
, 。
。
由性质三,有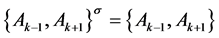 ,
,
由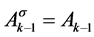 知
知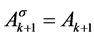 ,
,
由归纳假设,这样的对称变换固定正多边形上的每一点。
引理2. 固定正多面体的一个面及其上每个顶点,则这样的对称变换固定正多面体上的每个顶点。
证明:令对称变换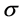 固定面
固定面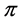 及其上的两相邻顶点。
及其上的两相邻顶点。
由引理1知, 固定
固定 上的每个点。
上的每个点。
用归纳法设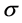 固定
固定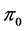 上的每个点。
上的每个点。
令 的所有相邻平面
的所有相邻平面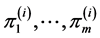 ,与这平面相交的边
,与这平面相交的边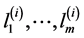 。
。
令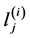 的两个顶点
的两个顶点 ,
,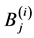 ,由
,由 ,知
,知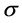 固定
固定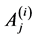 ,
,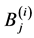 。
。
又由性质一知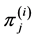 在对称变换后的像
在对称变换后的像 。
。
由引理1, 上的所有点也被唯一确定。由归纳假设,这样的对称变换固定正多面体上每一点。
上的所有点也被唯一确定。由归纳假设,这样的对称变换固定正多面体上每一点。
定理1. 正多面体自同构群的阶是边数的四倍。
证明: 令正多面体有 条边,
条边,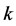 个顶点。
个顶点。
每一顶点的邻边(或相邻顶点)数: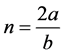 。
。
顶点所成集 。
。
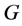 为正多面体的自同构群,显知
为正多面体的自同构群,显知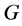 作用在
作用在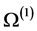 上都传递。
上都传递。
令 作用在
作用在 上关于
上关于 的稳定子群为
的稳定子群为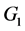 。
。
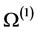 上与点
上与点 相邻的顶点顺时针依次是
相邻的顶点顺时针依次是 。
。
其中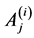 与
与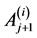 共面,
共面,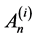 与
与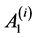 共面(
共面( )。
)。
令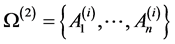 ,
,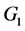 在
在 上传递,且关于
上传递,且关于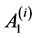 的稳定子群
的稳定子群 固定顶点
固定顶点 ,
, 。
。
由性质二知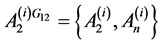 ,而由引理2知群
,而由引理2知群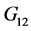 关于顶点
关于顶点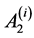 的稳定子群
的稳定子群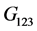 固定正多面体上的每一点,于是有:
固定正多面体上的每一点,于是有:
 证毕。可以注意到,正六面体与正八面体互为对偶图形,正十二面体与正二十面体互为对偶图形。事实上,如图3,以正六面体各个面中心为顶点,相邻面中心连线为边,可得到正八面体;同样地,以正八面体各个面中心为顶点,相邻面中心连线为边,可得到正六面体。故正六面体的自同构群与正八面体的自同构群等价。同理,依同样的方法可得图4,知正十二面体的自同构群与正二十面体的自同构群等价 [6] 。
证毕。可以注意到,正六面体与正八面体互为对偶图形,正十二面体与正二十面体互为对偶图形。事实上,如图3,以正六面体各个面中心为顶点,相邻面中心连线为边,可得到正八面体;同样地,以正八面体各个面中心为顶点,相邻面中心连线为边,可得到正六面体。故正六面体的自同构群与正八面体的自同构群等价。同理,依同样的方法可得图4,知正十二面体的自同构群与正二十面体的自同构群等价 [6] 。

Figure 3. The regular hexahedron and the regular octahedron are dual
图3. 正六面体与正八面体互为对偶

Figure 4. The regular dodecahedron and the regular icosahedron are dual
图4. 正十二面体与正二十面体互为对偶
于是有:
定理2 正六面体的自同构群与正八面体的自同构群等价,正十二面体的自同构群与正二十面体的自同构群等价。
3. 定理的证明
下求正四面体、正六面体、正十二面体的自同构群。
3.1. 正四面体
如图5,令正四面体的四个顶点分别是1,2,3,4,自同构群 。
。
由定理1有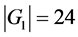 。
。
显知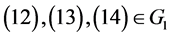 ,
,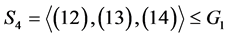 。
。
又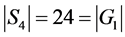 ,有
,有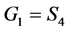 。
。
3.2. 正六面体
如图6,令正六面体的顶点集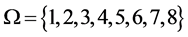 ,自同构群
,自同构群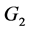 。
。
由性质四知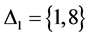 ,
, ,
,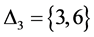 ,
,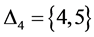 是
是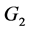 作用下的块。
作用下的块。
令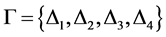 ,
,
 ,
, ,
,
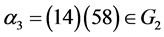 ,
,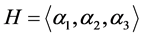 ,
,
显知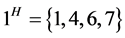 ,
, 在
在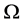 上不传递,故
上不传递,故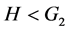 。
。
 在
在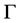 上的置换表示
上的置换表示 ,有
,有 ,
,

Figure 5. Regular tetrahedron
图5. 正四面体

Figure 6. Regular hexahedron
图6. 正六面体
又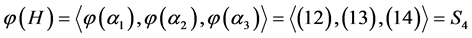 ,
,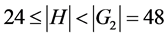 。
。
有 ,
,
而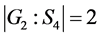 ,有
,有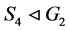 。
。
显知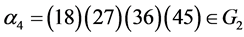 ,
,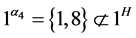 ,故
,故 ,于是有
,于是有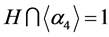 。
。
而 是显然的,并且
是显然的,并且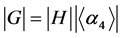 。
。
于是有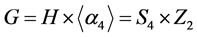 。
。
3.3. 正十二面体
如图7,对正十二面体顶点标记,令其自同构群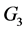 ,规定其上面的旋转变换
,规定其上面的旋转变换 ,反射变换
,反射变换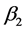 ,
,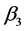 ,使它们在正多面体上的作用:
,使它们在正多面体上的作用:
 :上、下顶点中心为轴旋转72˚,
:上、下顶点中心为轴旋转72˚, :以
:以 ,
,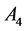 ,
, ,
, 所在平面为中心作反射,
所在平面为中心作反射, :以
:以 ,
, ,
, ,
, 所在平面作反射,其相应的置换表示如下:
所在平面作反射,其相应的置换表示如下:



若给正十二面体的各顶点标记如下:
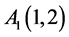 ,
,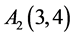 ,
,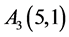 ,
,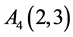 ,
, ,
, ,
,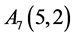 ,
,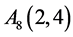 ,
,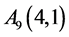 ,
,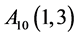 ,
,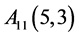 ,
, ,
, ,
, ,
, ,
, ,
,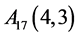 ,
, ,
,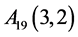 ,
,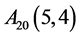 。
。
在上述标记中,令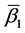 ,
, ,
, 为
为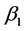 ,
, ,
, 对应坐标上的作用,则有:
对应坐标上的作用,则有:
 ,
,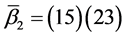 ,
,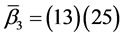 ,
,
又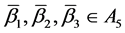 ,有:
,有: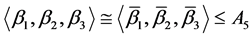 ,
,

Figure 7. The planar gragh of regular dodecahedron
图7. 正十二面体平面图
由于
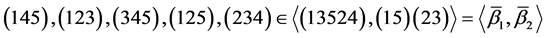
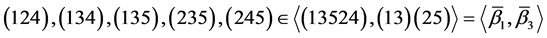
又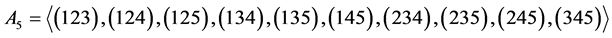
则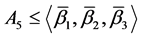 ,于是有
,于是有
由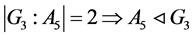 。
。
令 为正多面体关于重心的中心对称
为正多面体关于重心的中心对称
显知 ,
,
又 是单群知
是单群知
则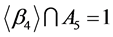 。
。
又 ,
,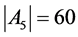 ,
,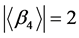
有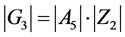
则 ,此时
,此时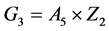 。
。
于是有正四面体的自同构群 ,正六面体的自同构群
,正六面体的自同构群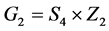 ,正十二面体的自同构群
,正十二面体的自同构群 ,由对偶性,正八面体的自同构群为
,由对偶性,正八面体的自同构群为 ,正二十面体的自同构群为
,正二十面体的自同构群为 。
。
现讨论星形正多边体:
由小星形十二面体的构造,知其可视为在正十二面体的每个面上衔接一个正五棱锥,故可构建小星形十二面体每一顶点与正十二面体相应面的一一对应,则此时具有相同的自同构群 。
。
由大星形十二面体的构造,知其可视为在正二十面体的每个面上衔接一个三棱锥,故可构建大星形十二面体每一顶点与正二十面体相应面的一一对应,此时具有相同的自同构群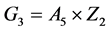 。
。
大十二面体与大二十面体顶点位置与正十二面体顶点位置一致,由于大十二面体的邻边当且仅当是正十二面体的邻边,故其自同构群同构,大二十面体的邻边顶点在正交变换下不变,故可构建与正十二面体相邻顶点的一一对应,因而自同构群依旧同构。
资助信息
本工作由国家自然科学基金11561078资助。
文章引用
余露,蔡琦. 正多面体自同构群的一点注记
A Note on the Automorphism Groups of Regular Polyhedrons[J]. 理论数学, 2017, 07(03): 186-192. http://dx.doi.org/10.12677/PM.2017.73024
参考文献 (References)
- 1. John, M. (1996) Permutation Groups. Springer, 5-17.
- 2. Mcmullen, P. (2007) Four-Dimensional Regular Polyhedra. Discrete & Computational Geometry, 38, 355-387.
- 3. Cunningham, P. (2016) Classification of Tight Regular Polyhedra. Journal Of Algebralc Combinatorics, 43, 665-691.
- 4. Itoh, O. (2017) A Natural Generalization of Regular Convex Polyhedra. Topology and Its Application, 219, 43-54. https://doi.org/10.1016/j.topol.2017.01.004
- 5. 张远达. 运动群[M]. 上海: 上海教育出版社, 1980.
- 6. 欧阳培昌, 占小根, 邓志云, 范发明. 正多面体对称群生成元的计算方法[J]. 井冈山大学学报, 2015, 36(6): 8-11.