Pure Mathematics
Vol.08 No.03(2018), Article ID:25069,6
pages
10.12677/PM.2018.83032
Weak BMO-Type Spaces Associated with Generalized Approximations to the Identity
Xiaojie Li
School of Mathematics and System Science, Beihang University, Beijing
Received: May 2nd, 2018; accepted: May 16th, 2018; published: May 25th, 2018

ABSTRACT
In this paper, we introduce a new weak BMO-type space
(
) on the homogeneous space
, which is associated with generalized approximations to the identity and generalizes
space. We show the equivalence of
space and
space, and give the interpolation theorem of
space and
space.
Keywords:Homogeneous Space,
Space, Interpolation

与广义逼近恒等式相关的弱BMO型空间
李肖杰
北京航空航天大学,数学与系统科学学院,北京
收稿日期:2018年5月2日;录用日期:2018年5月16日;发布日期:2018年5月25日

摘 要
在本篇文章中,我们引入了齐型空间
上与广义逼近恒等式相关的一类新的弱BMO型空间
,
,它是
空间的推广。我们证明了
空间与
空间的等价性,并给出了
空间与
空间的插值定理。
关键词 :齐型空间,
空间,插值
Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
19世纪60年代引入的经典
函数空间在现代调和分析中具有重要作用(可参见文献 [1] [2] )。设
,对任意的球
,称
,若
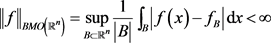 ,
,
其中
。在文献 [1] 中,John和Nirenberg证明了对任意的
,
空间与
空间等价,其中
空间定义如下:对任意的
,任意的球
,称
,若
.
众所周知,许多算子并不是从
到
有界的,而是从
到
有界的,例如Ricci-Stein震荡奇异积分算子,Carderón-Zygmund算子,Hardy-Littlewood极大算子。因此,弱型空间在算子理论研究中具有重要的意义。最近,王定怀等 [3] 引进了弱型BMO空间
,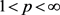 ,它是类似于弱型Lebesgue空间
所对应的BMO空间。并且他们证明了
与
的等价性。
,它是类似于弱型Lebesgue空间
所对应的BMO空间。并且他们证明了
与
的等价性。
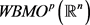 空间 [3] 定义如下:设
,对任意的球
,称
,若
空间 [3] 定义如下:设
,对任意的球
,称
,若
.
显然地,当
时,
。
此外,Duong和Yan [4] 引进了齐型空间
上适当的函数集
,并进一步引进了与广义逼近恒等式相关的一类新的BMO型函数空间
,它是经典BMO函数空间的推广。确切地说,设
是由核
(其衰减速度足够快)所定义的一类积分算子,对任意的
和满足
上某类增长条件的任意函数
,
.
称
,如果对任意的
,任意的球,
,
其中
,
是球B的半径,m是一个正常数。相应地,他们证明了对任意的, 空间与空间等价,其中 空间定义如下:称 ,如果对任意的
,任意的球
,
.
本文将文献 [4] 中的一些结论进行推广,引进了一类齐型空间
上与广义逼近恒等式相关的新的弱BMO型函数空间
,它是 [4] 中所引进的
空间的推广。而且我们证明了
空间和
空间的等价性,并对
空间与
空间的插值理论进行了研究。
在本文中,字母
表示与主要参数无关的常数,并且每一处取值不一定相等。
2. 预备知识和主要结果
我们首先回忆齐型空间上的一些基本定义,可见文献 [4] [5] [6] 。
给定非空集合
,满足下列条件的函数
:
称为
上的拟度量:
i) 对任意的
,
,
当且仅当
;
ii) 对任意的
,
;
iii) 存在常数
,使得对任意的
,
. (1)
拟度量d决定了一个拓扑,且对任意的
和
,所有的球
组成一个拓扑基。但当
时,这些球不一定为开集(可参见文献 [6] )。
定义1:设
是一个集合,称
是齐型空间,其中d是
上的拟度量,
是
上满足二倍条件的Borel测度,即存在常数
,对任意的
,
,使得
.
由上述二倍条件可得如下强齐次性:存在常数n和c,使得对任意的
,
和
,
, (2)
其中参数n是空间的维数。且存在
和
,
,使得对任意的
和
,
, (3)
事实上,
时,(3)式可由拟度量d的三角不等式和强齐次性直接得到。若
是
空间或多项式增长李群,则
。
定义2:设
是(6)式(见定义3)中的常数,且
,
,称
为以
为心的
型函数,如果f满足
. (4)
记
为所有
型函数的集合,若
,则
在
中的范数定义为
.
对一个固定的
,易知当
时,
是一个Banach空间。此外,对任意的
,
,且它们的范数等价。
记
,
其中
是(6)式中的常数。
定义3:设函数f满足增长条件(4),对任意的
,广义逼近恒等式
定义为:
.
设核
满足:对任意的
,
,
其中
, (5)
m是一个正常数,g是一个正的、有界的、递减函数且对某个
,
, (6)
其中N取值与(3)式中相同,n取值与(2)式中相同。
引理1 [4] :对任意的
,
,且当p取值不同时,范数
是等价的。
引理2 [4] :设
,T是一个次线性算子。若T在
上是有界的,
,且
,
则对任意的
,T在
上是有界的。
现在我们介绍与广义逼近恒等式
相关的
空间。
定义4:设
,对任意的
,任意的球
,称
,如果
.(7)
本文的主要结果如下。
定理1:设
,
是定义3中的广义逼近恒等式。则
,且它们的范数等价。
定理2:设
,
是齐型空间。假设
是满足(5)和(6)的广义逼近恒等式,且对任意的
,
几乎处处成立,即对几乎所有的
,
,则有
,且存在一个正常数c使得
. (8)
但反向不等式不一定成立。
注:注意到对(8)式来说,条件
几乎处处成立是必要的。事实上,对任意的
,考虑
,由(8)式得
。因此,对任意的
,
几乎处处成立。
由定理1和引理2,我们可得如下插值定理。
定理3:设T是一个次线性算子。对
,若T在
上是有界的,且
,
则对任意的
,T在
上是有界的。
3. 定理证明
为了证明定理1,我们首先证明以下两个引理。
引理3:设
,则有
,且存在一个正常数c使得
.(9)
证明:设
,由引理1得
引理4. 设
,则有
,且存在一个正常数c使得
.(10)
证明:设
,对任意给定的球
和
,
,
即
.
取
,
因此
.
于是
,
则
.
定理1的证明:对任意的
,由引理3可得
。因此,我们只需证明
。对任意的
,由引理1和引理4得
.
定理2的证明:当
时,由定理1得
,
再由命题2.5 [4] 和命题2.3 [3] 可得
,
因此,
。
下证(8)的反向不等式不一定成立。
设
,对任意的
,设
的核
,
对任意的
,令
。则对任意的
,
且
,但
。
因此,(8)的反向不等式不一定成立。
文章引用
李肖杰. 与广义逼近恒等式相关的弱BMO型空间
Weak BMO-Type Spaces Associated with Generalized Approximations to the Identity[J]. 理论数学, 2018, 08(03): 253-258. https://doi.org/10.12677/PM.2018.83032
参考文献
- 1. John, F. and Nirenberg, L. (1961) On Function of Bounded Mean Oscillation. Communications on Pure & Applied Mathematics, 14, 415-426. https://doi.org/10.1002/cpa.3160140317
- 2. Fefferman, C. and Stein, E.M. (1972) Spaces of Several Variables. Acta Mathematica, 129, 137-193.
https://doi.org/10.1007/BF02392215
- 3. 王定怀, 周疆. 一类新型BMO空间[J]. 数学学报, 2017, 60(5): 833-846.
- 4. Doung, X.T. and Yan, L.X. (2005) New Function Spaces of BMO Type, the John-Nirenberg Inequality, Interpolation, and Applications. Communications on Pure & Applied Mathematics, 58, 1375-1420. https://doi.org/10.1002/cpa.20080
- 5. Coifman, R.R. and Weiss, G. (1977) Extensions of Hardy Spaces and Their Use in Analysis. Bulletin of the American Mathematical Society, 83, 569-645. https://doi.org/10.1090/S0002-9904-1977-14325-5
- 6. Coifman, R.R. and Weiss, G. (1971) Analyse Hamonique Non-Commutative sur Certains Espaces Homogènes. Springer Berlin Heidelberg, 242. https://doi.org/10.1007/BFb0058946





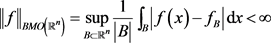 ,
,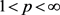 ,它是类似于弱型Lebesgue空间
所对应的BMO空间。并且他们证明了
与
的等价性。
,它是类似于弱型Lebesgue空间
所对应的BMO空间。并且他们证明了
与
的等价性。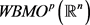 空间 [3] 定义如下:设
,对任意的球
,称
,若
空间 [3] 定义如下:设
,对任意的球
,称
,若