ABSTRACT

Firstly, this article presents the general expression of n-order ruled surface, and a sufficient and necessary condition for a surface to be a ruled surface. Secondly, it introduces the conceptions of minimum and tight rectilinear generators families, and obtains some interesting results. Lastly, it further studies ruled surfaces and puts them into two classes: compound and inseparable ruled surfaces, and obtains some important properties.

Keywords:Ruled Surface, n-Order Ruled Surface, Compound Ruled Surface, Minimum Rectilinear Generators Family, Tight Rectilinear Generators Family

n次直纹曲面及其分类

王继兴^*，赵 越

云南大学数学与统计学院，云南 昆明

收稿日期：2018年8月21日；录用日期：2018年9月6日；发布日期：2018年9月13日

摘 要

本文先给出了n次曲面的一般表达形式，从而得到了一个曲面是直纹曲面的一个充分必要条件。其次，对直纹曲面的直母线族提出了最小的、紧的等概念，并得到了一些有趣的结果。最后，展开了对直纹曲面的进一步研究，把其分为复合与不可分，并得了一些重要结果。

关键词 :直纹曲面，n次直纹曲面，复合直纹曲面，最小直母线族，紧的直母线族

Copyright © 2018 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

直纹曲面是生活中最常见，且应用最广泛的曲面 [1] [2] ，因此有许多文献对其从不同的角度进行了深入研究 [3] [4] [5] 。不过对高次直纹曲面几乎没有文献提及，因为高次曲面的一般表达式有点难度。本文巧妙地利用x，y，z对应的三个指数来定义系数，从而解决了n次曲面的一般表达形式。

大多数文献都把直纹曲面简单地定义为：一族直线生成的曲面或一条直线运动生成的曲面 [3] [4] [5] [6] 。本文认为这种定义方式太笼统以至于操作性不强，因此引入了操作性更强的定义。如何判断一个n( ≥ 1)次曲面是直纹曲面呢？本文给出了一个充分必要条件。这个结果在理论上有不小作用，但实际操作上并不方便。因此对直纹曲面进行了再认识，提出了复合直纹曲面等概念。这样，一个高次直纹曲面就可以通过较低次的直纹曲面不断复合得到。

本文也从细微的地方研究了直纹曲面，提出了最小的直母线族及紧的直母线族等概念，从而加深了对直纹曲面的认识。

2. n次直纹曲面

定义2.1：由三元n ( ≥ 1)次方程

${\displaystyle \underset{s=0}{\overset{n}{\sum }}{\displaystyle \underset{\begin{array}{l}i,j\\ i+j\le s\end{array}}{\sum }{a}_{\left(i,j,s-i-j\right)}}{x}^i{y}^j{z}^{s-i-j}}=0$ (1)

所表示的曲面叫做n次曲面，其中i，j及s都是非负整数，并且至少有一个n次项的系数不为0。当 $n\ge 3$ 时，称为高次曲面，否则称为低次曲面。并称函数

$F\left(x,y,z\right)={\displaystyle \underset{s=0}{\overset{n}{\sum }}{\displaystyle \underset{\begin{array}{l}i,j\\ i+j\le s\end{array}}{\sum }{a}_{\left(i,j,s-i-j\right)}}{x}^i{y}^j{z}^{s-i-j}}$ (2)

为n次曲面函数，简称曲面函数。

定义2.2：设 $\Sigma$ 为一个n次曲面。一条直线称为曲面 $\Sigma$ 的直母线，如果该直线在曲面 $\Sigma$ 上。曲面 $\Sigma$ 称为直纹曲面，如果对曲面 $\Sigma$ 上的任意一点 $M_0$ 都至少存在一条直母线经过它。

本文只讨论系数为实数且曲面点为实点的n次曲面。为简单计，有时用“曲面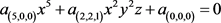”这种表达方式来代替“方程 $a_{\left(5,0,0\right)}{x}^5+a_{\left(2,2,1\right)}{x}^2{y}^{2}z+a_{\left(0,0,0\right)}=0$ 所表示的曲面”。为了更好的研究直线与曲面 $F\left(x,y,z\right)=0$ 的关系，本文引入示性函数

${\delta }_k\left(s,l,m,r\right)=\{\begin{array}{l}1,s-l-m-r=k\\ 0,其他\end{array}$

其中k，l，m，r，s都是非负整数。

设过曲面 $F\left(x,y,z\right)=0$ 上一点 $M_0=\left(x_0,y_0,z_0\right)$ 的直线方程为

$\{\begin{array}{l}x=x_0+Xt\\ y=y_0+Yt\\ z=z_0+Zt\end{array}$

代入(2)式确定的曲面函数 $F\left(x,y,z\right)$ 得

$\begin{array}{l}F\left(x_0+Xt,y_0+Yt,z_0+Zt\right)\\ ={\displaystyle \underset{s=0}{\overset{n}{\sum }}{\displaystyle \underset{\begin{array}{l}i,j\\ i+j\le s\end{array}}{\sum }{a}_{\left(i,j,s-i-j\right)}}}{\left(x_0+Xt\right)}^i{\left(y_0+Yt\right)}^j{\left(z_0+Zt\right)}^{s-i-j}\\ ={\displaystyle \underset{s=0}{\overset{n}{\sum }}{\displaystyle \underset{\begin{array}{l}i,j\\ i+j\le s\end{array}}{\sum }{a}_{\left(i,j,s-i-j\right)}}}{\displaystyle \underset{l=0}{\overset{i}{\sum }}{C}_i^l}{x}_0^l{\left(Xt\right)}^{i-l}{\displaystyle \underset{m=0}{\overset{j}{\sum }}{C}_j^m{y}_0^m{\left(Yt\right)}^{j-m}}{\displaystyle \underset{r=0}{\overset{s-i-j}{\sum }}{C}_{s-i-j}^r}{z}_0^r{\left(Zt\right)}^{s-i-j-r}\\ ={\displaystyle \underset{s=0}{\overset{n}{\sum }}{\displaystyle \underset{\begin{array}{l}i,j\\ i+j\le s\end{array}}{\sum }{a}_{\left(i,j,s-i-j\right)}}}{\displaystyle \underset{l=0}{\overset{i}{\sum }}{\displaystyle \underset{m=0}{\overset{j}{\sum }}{\displaystyle \underset{r=0}{\overset{s-i-j}{\sum }}{C}_i^l}}{C}_j^m{C}_{s-i-j}^r{x}_0^l{y}_0^m{z}_0^r{X}^{i-l}{Y}^{j-m}{Z}^{s-i-j-r}{t}^{i-l+j-m+s-i-j-r}}\end{array}$ (3)

$\begin{array}{l}={\displaystyle \underset{s=0}{\overset{n}{\sum }}{\displaystyle \underset{\begin{array}{l}i,j\\ i+j\le s\end{array}}{\sum }{a}_{\left(i,j,s-i-j\right)}}}{\displaystyle \underset{l=0}{\overset{i}{\sum }}{\displaystyle \underset{m=0}{\overset{j}{\sum }}{\displaystyle \underset{r=0}{\overset{s-i-j}{\sum }}{C}_i^l}}{C}_j^m{C}_{s-i-j}^r{x}_0^l{y}_0^m{z}_0^r{X}^{i-l}{Y}^{j-m}{Z}^{s-i-j-r}{t}^{s-l-m-r}}\\ ={\displaystyle \underset{k=0}{\overset{n}{\sum }}{G}_k\left(x_0,y_0,z_0,X,Y,Z\right)t^k}\\ ={\displaystyle \underset{k=1}{\overset{n}{\sum }}{G}_k\left(x_0,y_0,z_0,X,Y,Z\right)t^k}\end{array}$

其中

。

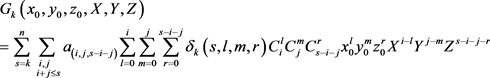特别地，当k = 0时，有 $G_0\left(x_0,y_0,z_0,X,Y,Z\right)=F\left(x_0,y_0,z_0\right)=0$ 。从而有下面的定理：

定理2.1：n次曲面 $F\left(x,y,z\right)=0$ 是直纹曲面的充分必要条件是对曲面上任意一点 $\left(x_0,y_0,z_0\right)$ 都存在一个对应的方向 $\left\{X,Y,Z\right\}$ 使得对任给的 $k=1,2,\cdots ,n$ ，有

$G_k\left(x_0,y_0,z_0,X,Y,Z\right)=0$ 。

证明：(必要性)若曲面是直纹曲面，则过曲面上任意一点 $\left(x_0,y_0,z_0\right)$ ，都有一条直线在曲面上。不妨设这条直线的方程为

$\{\begin{array}{l}x=x_0+Xt\\ y=y_0+Yt\\ z=z_0+Zt\end{array}$

由(3)知，它就会使得

$F\left(x_0+Xt,y_0+Yt,z_0+Zt\right)={\displaystyle \underset{k=1}{\overset{n}{\sum }}{G}_k\left(x_0,y_0,z_0,X,Y,Z\right)t^k}=0$

由t的任意性知 $G_k\left(x_0,y_0,z_0,X,Y,Z\right)=0$ ， $k=1,2,\cdots ,n$ 。

(充分性)若对曲面上任意一点都存在一个对应的方向 $\left\{X,Y,Z\right\}$ 使得对任给的 $k=1,2,\cdots ,n$ ，有 $G_k\left(x_0,y_0,z_0,X,Y,Z\right)=0$ 。

从而由(3)知，对任给的实数t，有

$F\left(x_0+Xt,y_0+Yt,z_0+Zt\right)={\displaystyle \underset{k=1}{\overset{n}{\sum }}{G}_k\left(x_0,y_0,z_0,X,Y,Z\right)t^k}=0$ ，这说明

整条直线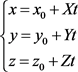在曲面上。从而定理成立。□

例1：证明4次曲面 $x^4-2x^{2}z-y^4-2y^{2}z-x^2+y^2+2z=0$ 是直纹曲面。

证明：记 $\begin{array}{l}F\left(x,y,z\right)=x^4-2x^{2}z-y^4-2y^{2}z-x^2+y^2+2z\\ =x^4-x^2{y}^2-2x^{2}z+x^2{y}^2-y^4-2y^{2}z-x^2+y^2+2z\\ =\left(x^2-y^2-2z\right)\left(x^2+y^2-1\right)\end{array}$ 。

设 $M_0=\left(x_0,y_0,z_0\right)$ 是曲面上任意点，且过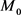的直线方程为

$\{\begin{array}{l}x=x_0+Xt\\ y=y_0+Yt\\ z=z_0+Zt\end{array}$ 。

下面去寻找使 $F\left(x_0+Xt,y_0+Yt,z_0+Zt\right)=0$ 的方向 $\left\{X,Y,Z\right\}$ 。考察

$\begin{array}{l}F\left(x_0+Xt,y_0+Yt,z_0+Zt\right)\\ =\left[{\left(x_0+Xt\right)}^2-{\left(y_0+Yt\right)}^2-2\left(z_0+Zt\right)\right]\left[{\left(x_0+Xt\right)}^2+{\left(y_0+Yt\right)}^2-1\right]\\ =\left[x_0^2+X^2{t}^2+2x_{0}Xt-y_0^2-Y^2{t}^2-2y_{0}Yt-2z_0-2Zt\right]\\ \times \left[x_0^2+X^2{t}^2+2x_{0}Xt+y_0^2+Y^2{t}^2+2y_{0}Yt-1\right]\\ =\left[\left(X^2-Y^2\right)t^2+2\left(x_{0}X-y_{0}Y-Z\right)t+\left(x_0^2-y_0^2-2z_0\right)\right]\\ \times \left[\left(X^2+Y^2\right)t^2+2\left(x_{0}X+2y_{0}Y\right)t+\left(x_0^2+y_0^2-1\right)\right]\end{array}$

$\begin{array}{l}=\left(X^2-Y^2\right)\left(X^2+Y^2\right)t^4+2\left(x_{0}X-y_{0}Y-Z\right)\left(X^2+Y^2\right)t^3\\ +\left(x_0^2-y_0^2-2z_0\right)\left(X^2+Y^2\right)t^2+2\left(X^2-Y^2\right)\left(x_{0}X+2y_{0}Y\right)t^3\\ +4\left(x_{0}X-y_{0}Y-Z\right)\left(x_{0}X+2y_{0}Y\right)t^2+2\left(x_0^2-y_0^2-2z_0\right)\left(x_{0}X+2y_{0}Y\right)t\\ +\left(X^2-Y^2\right)\left(x_0^2+y_0^2-1\right)t^2+2\left(x_{0}X-y_{0}Y-Z\right)\left(x_0^2+y_0^2-1\right)t\\ +\left(x_0^2-y_0^2-2z_0\right)\left(x_0^2+y_0^2-1\right)\end{array}$ (4)

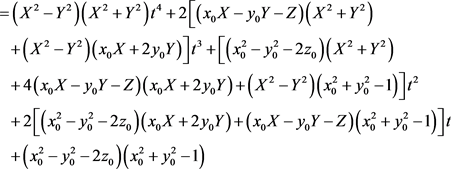
这样得到了一个关于t的一个4次方程，由前面定义的记号有

$G_4\left(x_0,y_0,z_0,X,Y,Z\right)=\left(X^2-Y^2\right)\left(X^2+Y^2\right)$ ，

$G_3\left(x_0,y_0,z_0,X,Y,Z\right)=2\left[\left(x_{0}X-y_{0}Y-Z\right)\left(X^2+Y^2\right)+\left(X^2-Y^2\right)\left(x_{0}X+2y_{0}Y\right)\right]$ ，

$G_2\left(x_0,y_0,z_0,X,Y,Z\right)=\left(x_0^2-y_0^2-2z_0\right)\left(X^2+Y^2\right)+4\left(x_{0}X-y_{0}Y-Z\right)\left(x_{0}X+2y_{0}Y\right)+\left(X^2-Y^2\right)\left(x_0^2+y_0^2-1\right)$

$G_1\left(x_0,y_0,z_0,X,Y,Z\right)=2\left[\left(x_0^2-y_0^2-2z_0\right)\left(x_{0}X+2y_{0}Y\right)+\left(x_{0}X-y_{0}Y-Z\right)\left(x_0^2+y_0^2-1\right)\right]$ ，

$G_0\left(x_0,y_0,z_0,X,Y,Z\right)=\left(x_0^2-y_0^2-2z_0\right)\left(x_0^2+y_0^2-1\right)=F\left(x_0,y_0,z_0\right)=0$ 。

由于 $M_0=\left(x_0,y_0,z_0\right)$ 是曲面上的一个点，于是有 $\left(x_0^2-y_0^2-2z_0\right)\left(x_0^2+y_0^2-1\right)=0$ 。从而 $\left(x_0,y_0,z_0\right)$ 必使 $\left(x_0^2+y_0^2-1\right)=0$ 或 $\left(x_0^2-y_0^2-2z_0\right)=0$ 。

i) 若 $x_0^2+y_0^2-1=0$ ，

则由(4)知：要使 $F\left(x_0+Xt,y_0+Yt,z_0+Zt\right)=0$ ，只需(4)的一个因式为0即可。由

$\left(X^2+Y^2\right)t^2+2\left(x_{0}X+y_{0}Y\right)t=0$

可以得到方向{0，0，1}，它使得

$G_4\left(x_0,y_0,z_0,X,Y,Z\right)=G_3\left(x_0,y_0,z_0,X,Y,Z\right)=G_2\left(x_0,y_0,z_0,X,Y,Z\right)=G_1\left(x_0,y_0,z_0,X,Y,Z\right)=0$ (5)

ii) 若 $x_0^2-y_0^2-2z_0=0$ ，

由(4)知：可考察 $\left(X^2-Y^2\right)t^2+2\left(x_{0}X-y_{0}Y-Z\right)t=0$ 。由

$\{\begin{array}{l}{X}^2-Y^2=0\\ x_{0}X-y_{0}Y-Z=0\end{array}$

知：若令X = 1，并取Y = 1，则 $Z=x_0-y_0$ 。可验证方向 $\left\{1,1,x_0-y_0\right\}$ 使得(5)式成立。这样，对曲面上任意一点 $\left(x_0,y_0,z_0\right)$ 都找到了一个方向 $\left\{X,Y,Z\right\}$ 使得对任给的k = 1，2，3，4，有

。

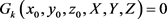从而由定理2.1知曲面 $x^4-2x^{2}z-y^4-2y^{2}z-x^2+y^2+2z=0$ 是一个直纹曲面。

3. 直母线族

定义3.1：设 $\Sigma$ 是一个n次曲面，且L是由一些直线构成的直线集。称L为曲面 $\Sigma$ 的一个直母线族，如果它满足下面两个条件：

i) L中的每一条直线都在 $\Sigma$ 上；

ii) 对曲面 $\Sigma$ 上的任意一点，在L中都至少有一条直线经过它。

定理3.1：一个曲面 $\Sigma$ 是直纹曲面的充分必要条件是它至少有一个直母线族。

证明：充分性显然。现证必要性：先令L为一空集。因为曲面 $\Sigma$ 是直纹曲面，故在曲面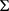上任取一点 $M_0$ ，都存在一条经过 $M_0$ 的直线 $l_0$ 在曲面上；如果L中没有 $l_0$ ，则把 $l_0$ 加入L。这样，当 $M_0$ 跑遍曲面 $\Sigma$ 时，就得到了一个直线构成的集合L。毫无疑问，它是曲面 $\Sigma$ 的一个直母线族。□

定义3.2：设L是n次曲面 $\Sigma$ 的一个直母线族。称L是紧的，如果在L中去掉任意一条直母线l，都会导致曲面 $\Sigma$ 上至少存在一点，使得L - {l}中没有一条直母线经过它。称L是最小的，如果对曲面上任意一点，L中都不存在两条(包括两条)以上的直母线经过它。称L是最大的，如果对曲面 $\Sigma$ 上的任意一点，经过它的任意一条直母线都属于L。

定理3.2：若曲面 $\Sigma$ 是一个直纹曲面，则它的最大直母线族是存在且唯一的。

证明：设 $M_0$ 为曲面 $\Sigma$ 上任意一点。并用记号L(M₀)表示曲面 $\Sigma$ 上过 $M_0$ 的所有直母线构成的集合，

则 ${\displaystyle \underset{M_{{}_0}\in \Sigma }{\cup }L\left(M_0\right)}$ 就是曲面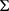的最大直母线族。(下面证明唯一性)设有另一个最大直母线族L，可证明

${\displaystyle \underset{M_{{}_0}\in \Sigma }{\cup }L\left(M_0\right)}=L$ 。事实上，任取 $l\in {\displaystyle \underset{M_{{}_0}\in \Sigma }{\cup }L\left(M_0\right)}$ ，由于L是最大直母线族，故 $l\in L$ ，因此。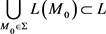

同理， $$ 。□

定理3.3：若曲面 $\Sigma$ 是一个直纹曲面，则它的最小的直母线族是紧的。

证明：设L是曲面 $\Sigma$ 的一个最小的直母线族，则对曲面上任意一点，L中都不存在两条(包括两条)以上的直母线经过它。这就导致在L中去掉任意一条直母线l，使得对l上的任意一点，在L - {l}中都没有直母线经过它。由紧的定义知，定理成立。□

虽然最大的直母线族是唯一的，但最小的却未必唯一。最小的一定是紧的，而紧的未必是最小的。

例3.1：直线族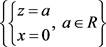与 $\left\{\{\begin{array}{l}y=a\\ x=0\end{array},a\in R\right\}$ 都是平面 $x=0$ 的最小直母线族。另外，在平面 $x=0$ 上，作三条直线族：

$L_1=\left\{\{\begin{array}{l}y=a\\ x=0\end{array},a<0\right\}$ ， $L_2=\left\{\{\begin{array}{l}z=a\\ x=0\end{array},a<1\right\}$ 及 $L_3=\left\{\{\begin{array}{l}z=1-y+a\\ x=0\end{array},a\ge 0\right\}$

则 $L_1\cup L_2\cup L_3$ 就是平面 $x=0$ 的一个紧的但非最小的母线族(见图1)。

单叶双曲面 $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{c^2}{c^2}=1$ 与双曲抛物面 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=2z$ 是两个重要的2次直纹曲面，并且是超出直观想象的。在文献 [6] 中分别得到了他们的两个直母线族，称为u族与v族。于是有：

引理3.1 [6] ：对于单叶双曲面(双曲抛物面)上的每一点，两族直母线中各有一条直母线经过它。

引理3.2 [6] ：单叶双曲面(双曲抛物面)上同族的任意两条直母线必异面。

定理3.4：单叶双曲面(双曲抛物面)的u族与v族都是它的最小直母线族。

证明：(先证u族)首先，由引理3.1知：u族是单叶双曲面(双曲抛物面)的直母线族。其次，由引理3.2知：u族中的任意两条直母线不相交，即单叶双曲面(双曲抛物面)上没有一个点有两条u族直母线经过它。因此u族是单叶双曲面(双曲抛物面)的最小直母线族。同理，v族也如此。□

4. 复合直纹曲面

定理4.1：若曲面 $F_1\left(x,y,z\right)=0$ 与是两个直纹曲面，则曲面 $\Sigma$ ：

图1. 平面的一个紧的但非最小的直母线族

$F_1\left(x,y,z\right)F_2\left(x,y,z\right)=0$

是直纹曲面。

证明：设L₁与L₂分别为曲面 $F_1\left(x,y,z\right)=0$ 与 $F_2\left(x,y,z\right)=0$ 对应的直母线族。则 $L_1\cup L_2$ 就是曲面 $\Sigma$ 的一个直母线族。首先， $L_1\cup L_2$ 中的任一直线是曲面 $\Sigma$ 的一条直母线。其次，在曲面 $\Sigma$ 上任取一点 $\left(x_0,y_0,z_0\right)$ ，就有

$F_1\left(x_0,y_0,z_0\right)F_2\left(x_0,y_0,z_0\right)=0$ 。

从而 $F_1\left(x_0,y_0,z_0\right)=0$ 或 $F_2\left(x_0,y_0,z_0\right)=0$ 。由于L₁与L₂分别为曲面 $F_1\left(x,y,z\right)=0$ 与 $F_2\left(x,y,z\right)=0$ 对应的直母线族，因此总有一条过 $\left(x_0,y_0,z_0\right)$ 的直母线l，它要么在曲面 $F_1\left(x,y,z\right)=0$ 上，要么在曲面上。从而直线l在曲面 $\Sigma$ 上。□

定理4.2：若曲面 $F_1\left(x,y,z\right)=0$ 是一个n ( ≥ 1)次直纹曲面，且 $F_2\left(x,y,z\right)=0$ 是一个m ( ≥ 1)次无实点的曲面，则曲面 $\Sigma$ ：

$F_1\left(x,y,z\right)F_2\left(x,y,z\right)=0$

是直纹曲面。

证明：设L₁是曲面 $F_1\left(x,y,z\right)=0$ 的一个直母线族。则L₁也是曲面 $\Sigma$ 的一个直母线族。首先，L₁中的直母线也是曲面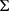的直母线。其次，在曲面 $\Sigma$ 上任取一点 $\left(x_0,y_0,z_0\right)$ ，必有 $F_1\left(x_0,y_0,z_0\right)F_2\left(x_0,y_0,z_0\right)=0$ 。因为 $F_2\left(x_0,y_0,z_0\right)\ne 0$ ，所以 $F_1\left(x_0,y_0,z_0\right)=0$ 。故L₁中有一条过 $\left(x_0,y_0,z_0\right)$ 的直母线l在曲面 $F_1\left(x,y,z\right)=0$ 上，从而直线l在曲面 $\Sigma$ 上。□

定理4.2揭示了一个n + m次直纹曲面可能本质上是一个n次直纹曲面。如4次直纹曲面

$\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}-1\right)\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+1\right)=0$

本质上等价于2次的单叶双曲面 $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$ (仅考虑实点是等价的；如果要考虑虚点，就不是等价的)。

定义4.1：如果一个n (≥2)次曲面能写成如下形式

$F_1\left(x,y,z\right)F_2\left(x,y,z\right)=0$

其中 $F_1\left(x,y,z\right)$ 与 $F_2\left(x,y,z\right)$ 的次都大于1，即曲面能分解成两个曲面之积，则称这个曲面为复合曲面(或可分的曲面)；并称 $F_1\left(x,y,z\right)=0$ 与 $F_2\left(x,y,z\right)=0$ 为它的分曲面；如果不能，则称为不可分曲面(或基本曲面)。

定理4.1揭示了一个高次的直纹曲面，可以通过较低次的直纹曲面之积的形式不断复合而成。设 $A_{i}x+B_{i}y+C_{i}z+D_i=0$ ， $i=1,2,\cdots ,n$ ，是n个不同的平面，则曲面 $F\left(x,y,z\right)={\displaystyle \underset{i=1}{\overset{n}{\prod }}\left(A_{i}x+B_{i}y+C_{i}z+D_i\right)}=0$ 就表示n个不同的平面构成的n次复合直纹曲面。

定理4.3：单叶双曲面与双曲抛物面都是不可分直纹曲面。

证明：因为他们都不能写成2个平面之积。□

接下来，考虑：一个曲面如果含有一条直母线，它是不是直纹曲面？

定理4.4：一个二次曲面，若它含有一条直母线，则它是直纹曲面。

证明：文献 [6] 证明了，任何二次曲面都可以化为17个标准方程形式之一。从这17标准方程来看，凡含有一条直母线的，都是直纹曲面。因此命题成立。□

对高次曲面来说，定理4.4的结论未必成立，即含有一条直母线的高次曲面未必是直纹曲面。如方程

$\left(z+c\right)\left(\frac{x^{\text{2}}}{a^{\text{2}}}+\frac{y^{\text{2}}}{b^{\text{2}}}+\frac{z^{\text{2}}}{c^{\text{2}}}-1\right)=0$

确定的曲面∑：是在平面 $z=-c$ 上放了一个椭球面 $\frac{x^{\text{2}}}{a^{\text{2}}}+\frac{y^{\text{2}}}{b^{\text{2}}}+\frac{z^{\text{2}}}{c^{\text{2}}}=1$ 。毫无疑问直线 $\{\begin{array}{l}y=x\\ z=-c\end{array}$ 在曲面上，但曲面∑不是直纹曲面。如果高次曲面不是复合曲面，结论又如何呢？因此提出下面的公开问题：

公开问题：如果一个不可分的高次曲面含有一条直母线，它是直纹曲面吗？

若命题“一个不可分的高次曲面含有一条直母线，则它是直纹曲面。”成立，则下面命题成立。

命题：如果一个可分的高次曲面含有一条直母线，则它有一个分曲面是直纹曲面。

基金项目

本研究得到国家自然科学基金(61663048)资助。

文章引用

王继兴,赵 越. n次直纹曲面及其分类
n-Order Ruled Surfaces and Their Classification[J]. 理论数学, 2018, 08(05): 534-541. https://doi.org/10.12677/PM.2018.85070

参考文献