河北工业大学理学院,天津
收稿日期:2022年4月14日;录用日期:2022年5月16日;发布日期:2022年5月23日

摘要
函数的凸性作为一种非常重要的几何性质,在证明不等式当中,函数的凸性发挥着重要作用。令
表示D上所有解析函数构成的空间,
。解析函数f的加权面积积分平均定义为
。本文主要研究对数凸函数,证明在什么条件下,
是对数凸函数。使得之前论文中的证明步骤变得简化。
关键词
凸性,对数凸性,解析函数

Logarithmic Convexity of Area Integral Means
Yucong Duan
School of Science, Hebei University of Technology, Tianjin
Received: Apr. 14th, 2022; accepted: May 16th, 2022; published: May 23rd, 2022

ABSTRACT
As a very important geometric property, the convexity of a function plays an important role in proving inequalities. Let
denote the space formed by all analytic functions on D,
. The weighted area integral average definition of the analytic function f is
. This paper mainly studies the logarithmic convex function, and proves under what conditions,
is a logarithmic convex function. This simplifies the proof steps in the previous paper.
Keywords:Convexity, Logarithmic Convexity, Analytic Function

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
令D表示复平面
上的开单位圆盘,
表示单位圆盘D上的标准勒贝格面积测度
对于任意的
,,加权面积测度定义如下
令
表示D上所有解析函数构成的空间,数学家Hardy最早提出解析函数的经典积分平均,即对于
,,f的经典积分平均定义如下
此定义被广泛的应用。并且在Hardy凸性定理中占据重要的地位。其中,Hardy凸性定理参见文献 [1]。具体表示为,假设
,且
,那么
1) 函数
关于r是单调增的;
2) 函数
关于
是对数凸函数。
对于
,,f的加权面积积分平均定义如下
解析函数的面积积分的对数凸性问题已经解决,详细参见 [2] [3] [4] [5] 以及 [7] [8] [9] [10] [11]。
在文献 [6] 中讨论了圆环上面积积分平均的对数凸性,证明得到假设
,,,且
,则函数
在
内是对数凸的。
令
表示定义在
内的实值函数的集合,其中函数
满足以下条件:
1)
;
2)
在
内是正的;
3)
在
内是连续的。
令M表示在
内
, 及
连续的函数M的集合。定义
(1)
本文主要讨论对于
, 解析函数
的面积积分平均
关于r的对数凸性的问题。即考虑什么条件下,
关于x是凸函数,需证明。
首先,本文详细介绍面积积分平均的对数凸性的研究背景知识以及一些引理知识。其次,利用证明论证得出相关定理,并通过反例来说其非凸的情况,最后进行总结。
2. 预备知识及相关定理
2.1. 预备知识
先对符号简单说明,在介绍相关的引理。
对于任意在
内上二阶可导的函数f,定义
(2)
以及
(3)
结合定义可以得到
(4)
以及
引理2.1假设
是在
内的二阶可导的函数,如果
是在
内是对数凸函数当且仅当函数
在
内是非负的。
注:引理2.1是文献[4]中的结论,证明过程便省略。
引理2.2假设
, 是在
内的二阶可微的正值函数,且
,如果
是在
内是对数凸函数当且仅当
在
内成立。
证明:我们对
直接进行求导运算,可得:
由于
, 以及
都是大于零,则根据(2)式,有
即可推得结论成立。
引理2.3假设
, 及
是在
内的二阶可微的正值函数,且在
内
,如果
在
内是对数凸函数当且仅当
在
内成立。
证明:我们对函数
直接进行求导运算,可得
因此,便有
结合(4)式,可得
成立。
对于
,有(2)式可知:
及
在
内是连续函数。因为
,有
在
内
。
2.2. 相关定理
定理2.1假设
, 以及
,当M满足对数凸函数时,函数
在
内是凸函数。
证明:
对于函数
及
,令
并且
,结合(2)式以及(3)式可以得到
,
这里,记
以及
对于函数
的对数凸性情况,根据引理2.3可知,只需要证明
在
上成立即可。其中
因为
,有
,因此,
直接对
求导
因为
,有
因为
,把
乘上
,可以得到
把
乘上
,再经过放缩可得
又因为
,有
,则
。因此,可以得到
在
上成立。得证。
2.3. 小结
对于任意
,函数
满足一定条件,面积积分平均是对数凸性。我们举例子来说明,可根据Maple画出相关例子的图像简单分析面积积分平均的为非凸的情形。例1:当
时,如图:
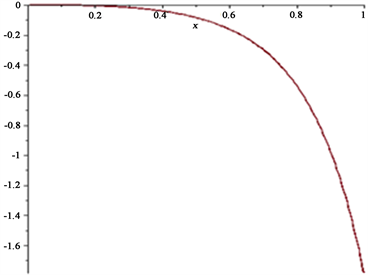
例2:当
时,如图:
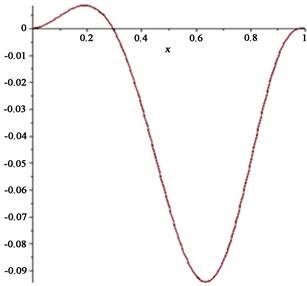
本文优势在于通过查阅资料,主要将函数的单调性、凸性与不等式的放缩以及简单地计算这几个方面的知识应用到一起,利用一种新的方法使文献 [7] 以及 [9] 中的证明过程更加简化,研究面积积分平均的对数凸性。
文章引用
段玉聪. 面积积分平均的对数凸性
Logarithmic Convexity of Area Integral Means[J]. 理论数学, 2022, 12(05): 749-756. https://doi.org/10.12677/PM.2022.125085
参考文献
- 1. Duren, P. (1970) Theory of Hp Spaces. Academic Press, New York, 9.
- 2. Cui, X.H., Wang, C.J. and Zhu, K.H. (2018) Area Integral Means of Analytic Functions in the Unit Disk. Canadian Mathematical Bulletin, 61, 509-517. https://doi.org/10.4153/CMB-2017-053-3
- 3. Wang, C.J., Xiao, J. and Zhu, K.H. (2015) Logarithmic Convexity of Area Integral Means for Analytic Functions II. Journal of the Australian Mathematical Society, 98, 117-128. https://doi.org/10.1017/S1446788714000457
- 4. Hörmander, L. (1994) Notions of Convexity, Birkhăuser, Bos-ton.
- 5. Shniad, H. (1953) Convexity Properties of Integral Means of Analytic Functions. Pacific Journal of Mathematics, 3, 657-666. https://doi.org/10.2140/pjm.1953.3.657
- 6. Wang, C.J. and Xiao, J. (2016) Addendum to “Gaussian integral means of entire functions”. Complex Analysis and Operator Theory, 10, 495-503. https://doi.org/10.1007/s11785-015-0447-x
- 7. Hu, Q.X. and Wang, C.J. (2020) Convexity for Area Integral Means. Journal of Mathematical Analysis and Applications, 491, Article No. 124345. https://doi.org/10.1016/j.jmaa.2020.124345
- 8. Cho, H.R. and Zhu, K.H. (2012) Fock-Sobolev Spaces and Their Carleson Measures. Journal of Functional Analysis, 263, 2483-2506. https://doi.org/10.1016/j.jfa.2012.08.003
- 9. Wang, C.J. and Yang, W.J. (2019) Area Integral Means over the Annuli. Journal of Mathematical Analysis and Applications, 473, 510-518. https://doi.org/10.1016/j.jmaa.2018.12.064
- 10. Wang, C.J. and Zhu, K.H. (2014) Logarithmic Convexity of Area Integral Means for Analytic Functions. Mathematica Scandinavica, 114, 149-160. https://doi.org/10.7146/math.scand.a-16643
- 11. Xiao, J. and Zhu, K.H. (2011) Volume Integral Means of Holomorphic Functions. Proceedings of the American Mathematical Society, 139, 1455-1465. https://doi.org/10.1090/S0002-9939-2010-10797-9







