Advances in Applied Mathematics
Vol.
09
No.
04
(
2020
), Article ID:
35178
,
12
pages
10.12677/AAM.2020.94065
Stochastic Dynamics Analysis of Permanent Magnet Synchronous Motor Model
Zhengwei Ye, Shengwen Deng, Wang Qin, Xiangling Liang
School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou Gansu
Received: Apr. 3rd, 2020; accepted: Apr. 15th, 2020; published: Apr. 22nd, 2020

ABSTRACT
Firstly, the nonlinear differential equation of the PMSM systems was established by introducing random terms into the PMSM model based on synchronous rotating coordinates. The stochastic center manifold is used to reduce the dimension of the stochastic systems, and then the Ito differential equations are obtained by the stochastic average method. Then, by using Lyapunov index and singular boundary theory, the local and global stability of the systems are discussed, and the conditions of stability are obtained. The D-bifurcation and P-bifurcation behavior of the systems is analyzed based on the stochastic average method for the quasi-integrable Hamiltonian systems. Finally, the appropriate bifurcation parameters are selected for numerical simulation, and the bifurcation positions are verified.
Keywords:Permanent Magnet Synchronous Motor Model, Hamilton System, Stochastic Stability, Stochastic Bifurcation

永磁同步电机模型的随机动力学分析
叶正伟,邓生文,秦旺,梁相玲
兰州交通大学数理学院,甘肃 兰州
收稿日期:2020年4月3日;录用日期:2020年4月15日;发布日期:2020年4月22日

摘 要
首先基于同步旋转坐标的永磁同步电机模型引入随机噪声项,建立永磁同步电机系统的非线性微分方程,运用中心流形定理对随机系统进行降维处理,再运用随机平均法得到 微分方程;其次根据Lyapunov指数法讨论了系统的局部稳定性、应用奇异边界理论讨论了全局稳定性并得到稳定性条件;根据拟不可积Hamilton系统随机平均法分析了系统的D-分岔和P-分岔;最后选取合适的分岔参数进行数值模拟,并验证了分岔位置。
关键词 :永磁同步电机模型,Hamilton系统,随机稳定性,随机分岔

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
永磁同步电机是一种新型同步电机,因其高精度、高功率密度、高转矩惯性比、小体积等优越性能广泛应用于航空航天、船舶电力、电动汽车等领域,但许多学者在研究永磁同步电机时会忽略或近似波动因素(如忽略温度和阻尼影响、如空间磁场近似视为正弦分布等),讨论确定系统下的动力学行为,文献 [1] 在理想化条件下研究了车用永磁同步电机模型的抗扰和控制,其分析过程存在诸多限制,得不到更接近实际的结果;文献 [2] 在讨论永磁同步电机模型时指出了如磁链耦合等影响,并根据影响因素对系统进行了优化,但其优化是基于结构上进行的,并未对影响参数改进处理;文献 [3] 在确定的永磁同步电机模型下,引入了噪声干扰,但其动力学行为分析仍是基于规律性的正弦扰动。我们已知永磁同步电机工作时影响因素,电阻会受温度影响;摩擦系数会受阻尼影响;电感会受外部磁场影响。为了更好的提高永磁同步电机的鲁棒性需考虑上述影响参数,我们通过引入随机项对系统进行随机激励耗散的建立,便可获得一种更接近实际情况的描述思路。
目前,针对永磁同步电机模型,应用Hamilton理论进行分析的研究非常稀少,而随机动力系统的研究已有大量的理论方法,文献 [4] [5] [6] [7] 介绍了随机激励耗散Hamilton的知识,文献 [8] 介绍了调速器系统的随机分岔行为,这样便有机械系统引入随机噪声的参考可寻。本文在文献 [2] 的模型上引入了随机项,建立了随机参数激励下的永磁同步电机模型,首先运用中心流形定理对系统进行降维化简,再运用随机平均法得到Itô微分方程;接着讨论了系统稳定性并得出稳定性条件;最后进行分岔分析且选取合适的参数进行数值模拟。
2. 随机参数激励下的永磁同步电机模型建立
在交直轴电感近似相等的情形下,永磁同步电机基于同步旋转坐标下的数学模型 [2] 表示如下:
(1)
系统变量及参数的物理意义: 为d-q轴定子电流, 为d-q轴定子电压,w为转子机械角速度,R为定子电阻,L为定子电感, 为负载转矩,J为转动惯量,B为粘滞摩擦系数,P为极对数, 为转子磁链,所涉及参数均为正数,求得非负平衡点为: 。
考虑系统(1)中参数电阻R,电感L,摩擦系数B,转子磁链 会受内部温度外部磁场、阻尼、耦合等因素影响变得不稳定,把影响因素视为白噪声,对其引入随机项:
,得到一个新的随机非线性微分方程:
(2)
其中 为白噪声强度, 为零均值白噪声,其中 接着令 ,系统(2)可化为:
(3)
其中:
3. 永磁同步电机模型的处理
据上述推导关系知,系统(3)在 处的性质等价系统(2)在平衡点 的性质,我们可把系统(2)在 的稳定性转化为系统(3)在 处的来讨论。模型(3)的特征方程为:
(4)
其中:
求得方程(4)的特征值为: ,
令
,,当参数
趋近于零时,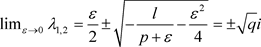 ,
此时点
将退化为系统(3)的临界焦点,具有局部不变流行的性质。
,
此时点
将退化为系统(3)的临界焦点,具有局部不变流行的性质。
令 与 的关系式如下:
则系统(3)可变为:
(5)
其中:
此时系统(3)在原点附近具有局部不变流行:
对系统(5)降维可近似表示为下式:
(6)
其中:
且h满足 的全微分 ,所以将 的全微分代入(6)式得,
我们要求解的中心流形可用下式来逼近:
代入上述方程两边相同幂系数合并得:
忽略高阶项,可进一步得到系统(7)
(7)
令 ,进行极坐标变换系统(7)可转化为:
(8)
其中:
在解决系统(8)时,精确解不易求出,但可基于Khasminskii极限定理 [4] [9] [10] [11],当白噪声强度充分小时,其反应 弱收敛于一个二维的马尔可夫扩散过程,运用随机平均法,系统(8)可得到Itô随机微分方程:
(9)
对于上述二维马尔可夫扩散过程,计算它的转换概率密度,方程(9)表达为:
(10)
其中:
根据扩散矩阵,可以得到平均振幅是一维的马尔可夫过程,如下式(11):
(11)
这样,在讨论模型的稳定性和随机分岔时获得一个思路,即根据参数的随机概率密度分布,分析在概率密度意义下平均振幅的稳定性和临界分岔。
4. 稳定性分析
4.1. 局部稳定性
讨论局部稳定时,基于Oseledec乘性遍历理论 [4] 和最大Lyapunov指数法,随机方程平凡解在概率意义下稳定的充要条件为:最大Lyapunov指数 。
我们讨论线性Itô随机微分方程的稳定性,首先令 ,即讨论 时方程(11)的稳定性,此时方程变为:
(12)
对微分方程(12)求解得,
其中 ,
根据拟不可积Hamilton系统理论 [5],线性Itô随机微分方程的Lyapunov指数近似表示为:
。
这样可得方程(12)的Lyapunov指数:
① 当 ,即 时,线性Itô随机微分方程(11)是局部稳定的,即原系统(2)在平衡点处是稳定的;
② 当 ,即 时,线性Itô随机微分方程(11)是局部不稳定的,即原系统(2)在平衡点处是不稳定的。
4.2. 全局稳定性
在分析局部稳定性时,应用Oseledec乘性遍历理论和最大Lyapunov指数判定方法,但该理论方法只适用于做局部稳定性判断,接下来分析全局稳定性,我们可用奇异边界理论 [4] [5] 对其全局稳定性做分析判断。
首先介绍奇异边界理论,我们已知r,此外还有扩散指数 ;漂移指数 ;特征指数 。
I) 如果有 ,即 ,系统为第一类奇异边界,第一类边界下:
当 时, 是排斥自然边界, 是吸引自然边界, 是严格自然边界;
II) 如果有 ,即 ,系统为第二类奇异边界,第二类边界下:
当 , 时, 是排斥自然边界, 是吸引自然边界, 且 是严格自然边界;
当 时, 是进入边界。
上述为奇异边界理论介绍,接下来我们分两种情形进行分析,即 情形。
1) 当 时,系统如上述(12), 时系统(12)为第一类奇异边界,经过计算可以得, ,,
,则有: 是排斥自然边界, 是吸引自然边界,
是严格自然边界;
时系统(12)为第二类奇异边界,经过计算可以得, ,,
则有, 是排斥自然边界, 是吸引自然边界, 是严格自然边界。
综上可得出结论:
① 当 , 为吸引自然边界, 是排斥自然边界,则Itô微分方程(11)有概率意义下稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是稳定的;
② 当 , 为排斥自然边界, 是吸引自然边界,则Itô微分方程(11)有概率意义下不稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是不稳定的;
③ 当
,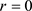 和
为严格自然边界。
和
为严格自然边界。
2) 当 时,系统为方程(11), 系统(11)是第一类奇异边界,经过计算可得到, ,,
,则有: 是排斥自然边界, 是吸引自然边界, 是严格自然边界; 系统(11)为第二类奇异边界,经计算 ,,则 是二类奇异边界中的进入边界。
综上可以得出结论:
① 当 , 是吸引自然边界,且 是进入边界,则Itô微分方程(11)有概率意义下稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是稳定的;
② 当 , 时为排斥自然边界,而 是进入自然边界,则Itô微分方程(11)有概率意义下不稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是不稳定的;
③ 当 , 时为严格自然边界。
5. 随机分岔分析
随机分岔理论 [4] [5] 是通过研究参数的变化,对随机动态系统进行性态分析,我们将应用拟不可积Hamilton系统随机平均法来解决随机分岔动力学行为。
5.1. 随机D-分岔分析
当Itô随机微分方程(11)中 时,方程即为:
(13)
由于 方程变为不发生分岔的确定系统,我们讨论 时的情形,令 ,,方程(13)生成的连续动态系统为:
(14)
式(14)为方程(13)以x为初值的唯一强解。当 时,0是 的固定点,对此固定点, 是Stratonovich的随机意义下的激参,设 有界,则对 满足椭圆性条件的 ,保证最多有一个平稳概率,则对应的FPK方程为:
(15)
其中,令 得到与方程(15)相应的平稳概率密度:
(16)
这样,则该动态系统可能有不动点、非平凡平稳两种平稳状态,且二者不变测度 和 的密度分别为 和(16)式,此时还需确定两不变测度的Lyapunov指数,解线性Itô随机微分方程(13)为:
(17)
已知系统测度的Lyapunov指数:
(18)
根据公式 得,不动点状态的Lyapunov指数:
(19)
设 有界, 可积,将式(17)代入方程(18),非平凡平稳状态的Lyapunov指数为:
(20)
令 ,则根据二者不变测度的Lyapunov指数可判定,当 时前者不变测度稳定,当
时后者不变测度稳定,即系统(2)的一个D-分岔在 处发生。
我们进一步处理系统(16)可以得到:
(21)
其中:c为归一化常数, ,当 ,即 时, 是一个 函数,当 ,即 时, 是 在该区间的最大值点,所以随机系统(2)发生D-分岔的临界条件为, ,即 。
当Itô随机微分方程(11)中 时,令 ,,则方程(11)变为:
(22)
当
时,系统为确定分岔-叉形分岔,当
时,讨论
时,有唯一密度为
不变测度
;
时,动态系统的平衡状态相应的不变测度分别为
和非平凡平稳状态测度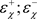 ,密度为:
,密度为:
(23)
(24)
其中 ,则根据式(19)得 的Lyapunov指数为:
(25)
根据方程(20),(23),(25)可得两个非平凡平稳状态测度 的Lyapunov指数为:
(26)
所以 时,随机系统(2)的发生D-分岔。
5.2. 随机P-分岔分析
令 ,,则方程(11)变为:
(27)
可得到方程(27)的FKP方程为:
(28)
其初值条件为: ,,, 为扩散过程的转移概率密度, 的不变测度是平稳概率密度,若令 ,则退化系统的解为:
对系统进行P-分岔分析时,我们的思路是由线性Itô随机微分方程的概率密度
计算不变测度极值,进而分析分岔。根据Namachivay’s理论 [4] [10] [12],当噪声
趋于0时,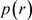 的极值趋表现稳态特征,当系统响应
是遍历的,由乘积遍历性定理得
是样本轨线在 的邻域内访问时间的度量。
的极值趋表现稳态特征,当系统响应
是遍历的,由乘积遍历性定理得
是样本轨线在 的邻域内访问时间的度量。
若 在 处为极大值,轨线在 的邻域内停留时间较长,说明 在概率意义下是稳定点;若 在 处为极小值,轨线在 的邻域内停留时间较短,说明 在概率意义下是不稳定点。
6. 数值模拟
综上可知原系统的响应过程为 ,且 ,所以我们主要分析 的联合概率密度 即可,在实际意义下,赋值参数 ,使得 ,在此情况
下,给出平稳概率密度函数和联合概率密度函数模拟图像。
若设 ,图1中左图表示,取不同的负值 ,平稳概率密度函数是单调递减函数,且随 的增大图像减势变弱,右图表示 时联合概率密度图像呈现单峰尖状;图2中左图表示在 附近,随 值增大平稳概率密度函数从递减变为有极值状态,右图表示 时联合概率密度图像呈现单峰状,说明此时并未发生分岔;图3中左图表示,取不同的正值 ,平稳概率密度函数是极值函数,且随 的增大平稳概率密度函数极值峰谷趋于平缓,右图表示 时联合概率密度函数呈现火山口形状,则系统在临界点 后发生了分岔。

Figure 1. The left figure shows stationary probability density function image of ; The right figure shows joint probability density function image of
图1. 左图表示 分取−0.22,−0.12,−0.02时平稳概率密度函数图像;右图表示 联合概率密度函数图像
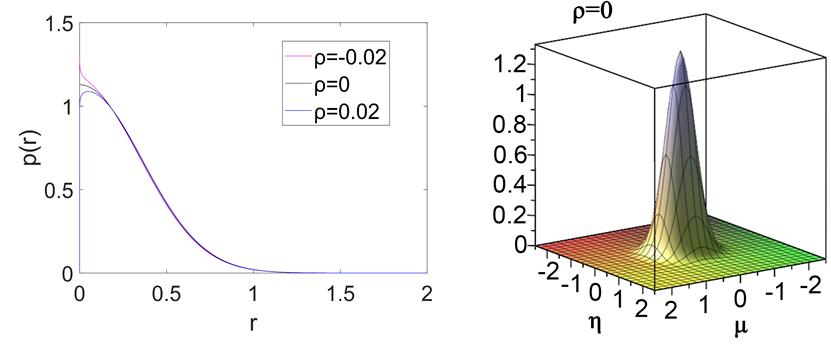
Figure 2. The left figure shows stationary probability density function image of ; The right figure shows joint probability density function image of
图2. 左图表示 分取−0.02,0,0.02时平稳概率密度函数图像;右图表示 联合概率密度函数图像
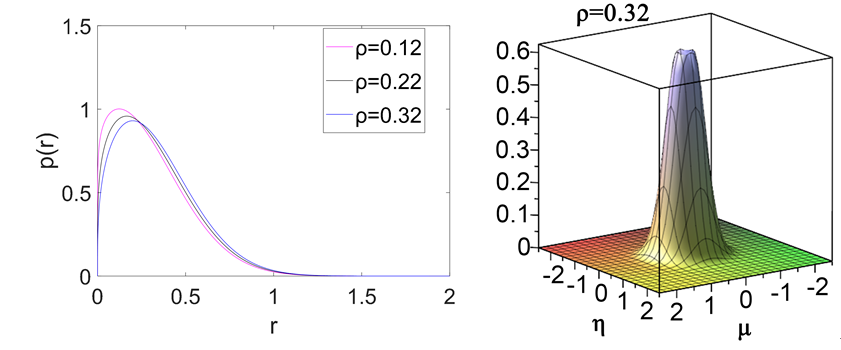
Figure 3. The left figure shows stationary probability density function image of ; The right figure shows joint probability density function image of
图3. 左图表示 分取0.12,0.22,0.32时平稳概率密度函数图像;右图表示 联合概率密度函数图像
7. 结论
本文讨论了在随机参数激励下永磁同步电机的稳定性和分岔,把随机参数视为白噪声,运用随机激耗散的Hamilton理论,对系统的动力学行为进行分析,结合实际意义选取分岔参数 ,根据数值模拟结果得出当 时系统发生分岔行为,说明此时永磁同步电机系统有可能会变得不稳定。
文章引用
叶正伟,邓生文,秦 旺,梁相玲. 永磁同步电机模型的随机动力学分析
Stochastic Dynamics Analysis of Permanent Magnet Synchronous Motor Model[J]. 应用数学进展, 2020, 09(04): 539-550. https://doi.org/10.12677/AAM.2020.94065
参考文献
- 1. 高华鑫. 基于变结构自抗扰的车用PMSM模型预测控制[J]. 计算机应用与软件, 2018, 35(6): 83-87.
- 2. 兰永红, 陈才学. 基于降维观测器的永磁同步电机无速度传感器反推控制方法[J]. 控制工程, 2019, 26(10): 1843-1849.
- 3. Ma, C.Y., et al. (2011) Sliding Mode Control of Chaos in the Noise-Perturbed Permanent Magnet Synchronous Motor with Non-Smooth Air-Gap. Mining Science and Technology, 21, 835-838. https://doi.org/10.1016/j.mstc.2011.05.035
- 4. 朱位秋. 非线性随机动力学与控制-Hamilton理论框架[M]. 北京: 科学出版社, 2003.
- 5. 朱位秋, 蔡国强. 随机动力学引论[M]. 北京: 科学出版社, 2017.
- 6. Liu, W.Y. and Zhu, W.Q. (2014) Stochastic Stability of Quasi-Integrable and Non-Resonant Hamiltonian Systems under Parametric Excitations of Combined Gaussian and Poisson White Noises. International Journal of Nonlinear Mechanics, 58, 191-198.https://doi.org/10.1016/j.ijnonlinmec.2013.09.010
- 7. Liu, W.Y. and Zhu, W.Q. (2014) Stochastic Stability of Quasi-Integrable and Resonant Hamiltonian Systems under Parametric Excitations of Combined Gaussian and Poisson White Noises. International Journal of Nonlinear Mechanics, 67, 52-62. https://doi.org/10.1016/j.ijnonlinmec.2014.08.003
- 8. Zhang, J.G. and Chu, Y.D. (2017) The Invariant Measure and Stationary Probability Density Computing Model Based Analysis of the Governor System. Cluster Computing, 20, 1437-1447.https://doi.org/10.1007/s10586-017-0817-4
- 9. Kha’Minskii, R.Z. (2019) Necessary and Sufficient Conditions for the Asymptotic Stability of Linear Stochastic Systems. 12, 144-147.https://doi.org/10.1137/1112019
- 10. Lim, Y. and Cai, G. (2004) Probabilistic Structural Dynamics. McGraw-Hill: McGraw-Hill Professional, Publishing.
- 11. Arnold, L. (1998) Random Dynamical Systems. Springer, New York. https://doi.org/10.1007/978-3-662-12878-7
- 12. Namachchivaya, N. (1990) Stochastic Bifurcation. Applied Mathematics and Computation, 38, 101-159. https://doi.org/10.1016/0096-3003(90)90051-4