Statistics and Application
Vol.06 No.01(2017), Article ID:20017,6
pages
10.12677/SA.2017.61010
Four Methods for Estimating Unknown Parameters in Panel Model
Wenqian Kang
Institute of Medical Information of Yunnan Province, Kunming Yunnan

Received: Mar. 10th, 2017; accepted: Mar. 26th, 2017; published: Mar. 29th, 2017

ABSTRACT
In this paper, four methods for estimating the unknown parameters in Panel model are discussed, which are least squares estimator, Within estimator, Between estimator and two-stage estimator. This paper shows the corresponding expressions of four estimation methods, and compares the advantage of four methods under certain conditions briefly.
Keywords:Least Squares Estimator, Within Estimator, Between Estimator, Two-Stage Estimator
浅谈Panel模型中未知参数的四种估计方法
康文倩
云南省医学信息研究所,云南 昆明
收稿日期:2017年3月10日;录用日期:2017年3月26日;发布日期:2017年3月29日

摘 要
本文整理了Panel模型中未知参数的四种估计方法,分别是最小二乘估计,Within估计,Between估计和两步估计。给出了四种估计方法对应的表达式,并且简单讨论了一定条件下四种估计的优良性。
关键词 :最小二乘估计,Within估计,Between估计,两步估计

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Panel模型是一种线性回归模型,也称为平面数据模型。这类模型可用来分析个体间的差异情况,也能用来描述个体的动态变化特征,在计量经济学、市场分析、区域经济研究、机械加工等领域有着广泛的应用。
考虑如下含一个随机效应的Panel模型
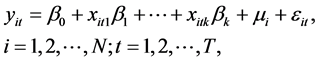 (1.1)
(1.1)
这里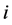 为代表个体的下标,
为代表个体的下标,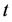 为代表时间的下标。
为代表时间的下标。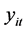 表示第
表示第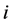 个个体在时刻
个个体在时刻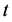 的观测值,
的观测值,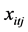 表示第
表示第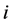 个个体上第
个个体上第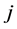 个自变量在时刻
个自变量在时刻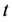 的取值,
的取值,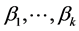 为通常的回归系数,
为通常的回归系数, 为第
为第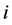 个个体的效应。假如这
个个体的效应。假如这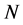 个个体是从足够大的总体中随机抽取的,那么个体效应是随机的,
个个体是从足够大的总体中随机抽取的,那么个体效应是随机的,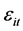 为随机误差。一般假设所有的
为随机误差。一般假设所有的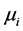 和
和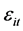 都互不相关,并且
都互不相关,并且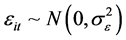 ,
,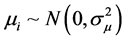 。记
。记
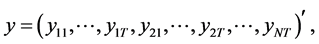
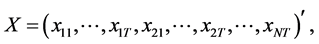
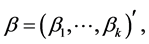
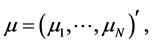
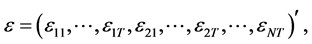
其中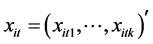 ,于是模型(1.1)可以写成矩阵形式
,于是模型(1.1)可以写成矩阵形式
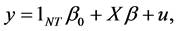 (1.2)
(1.2)
其中 ,
,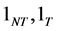 分别表示分量全为1的
分别表示分量全为1的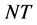 维,
维,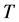 维列向量,符号“
维列向量,符号“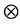 ”表示Kronecker乘积。
”表示Kronecker乘积。
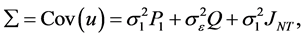
其中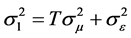 ,
, ,
,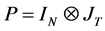 ,
,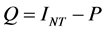 ,
,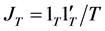 。
。
矩阵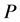 ,
,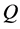 ,
,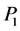 和
和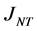 有如下重要性质。
有如下重要性质。
引理1.1 [1] 1)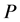 ,
,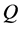 ,
,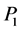 和
和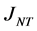 都是对称幂等阵,它们的秩分别是
都是对称幂等阵,它们的秩分别是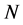 ,
,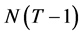 ,
,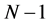 和1。
和1。
2)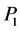 ,
,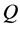 和
和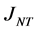 两两正交,即
两两正交,即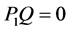 ,
,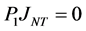 ,
,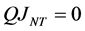 。
。
3)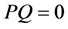 ,
,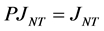 ,
,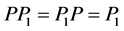 。
。
引理可利用王松桂 [1] 等中相关结论加以证明。
2. 四种估计方法
在Panel模型中,我们总假设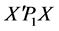 和
和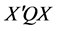 是可逆的,
是可逆的, 。实际中的一般问题,这些条件往往是满足的。下面讨论未知参数向量
。实际中的一般问题,这些条件往往是满足的。下面讨论未知参数向量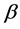 的几种估计。
的几种估计。
如果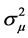 和
和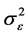 已知,则
已知,则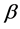 的最佳线性无偏估计(BLU)为
的最佳线性无偏估计(BLU)为
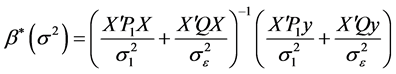 (1.3)
(1.3)
记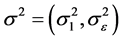 ,它的协方差阵为
,它的协方差阵为
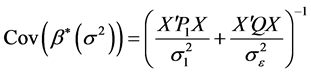
然而在实际应用中,由于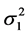 和
和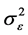 都是未知的,因此并不能实际应用。于是,我们寻求一些其它的估计方法。
都是未知的,因此并不能实际应用。于是,我们寻求一些其它的估计方法。
2.1. 最小二乘估计
在(1.3)中令 ,即
,即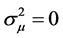 时,可以得到
时,可以得到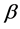 的最小二乘(LS)估计
的最小二乘(LS)估计
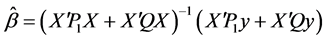
2.2. Between估计
对模型(1.2)分别左乘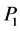 和
和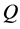 ,得到
,得到
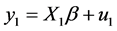 (1.4)
(1.4)
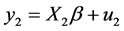 (1.5)
(1.5)
这里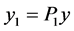 ,
, ,
,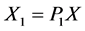 ,
,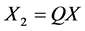 ,
,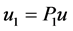 ,
,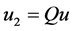 。
。 和
和 的均值都为零,它们的协方差阵分别为
的均值都为零,它们的协方差阵分别为
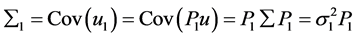
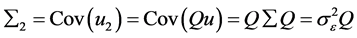
应用最小二乘统一理论,可以得到线性模型(1.4)中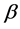 的最佳线性无偏(BLU)估计,记作
的最佳线性无偏(BLU)估计,记作
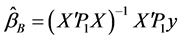
此即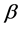 的Between估计,其协方差阵为
的Between估计,其协方差阵为
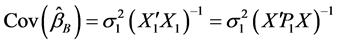
2.3. Within估计
同样应用最小二乘统一理论,得到线性模型(1.5)中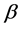 的最佳线性无偏(BLU)估计,记作
的最佳线性无偏(BLU)估计,记作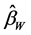 ,为
,为
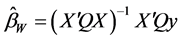
称为Within估计 [2] ,其协方差阵为
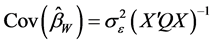
2.4. 两步估计
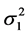 和
和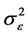 已知时我们已经得到回归系数
已知时我们已经得到回归系数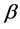 的最佳线性无偏估计。由于
的最佳线性无偏估计。由于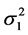 和
和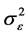 都是未知的,我们可以先找到
都是未知的,我们可以先找到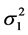 和
和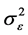 的某种估计,然后再代入(1.3),这样所得的估计称为两步估计。下面先来构造
的某种估计,然后再代入(1.3),这样所得的估计称为两步估计。下面先来构造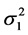 和
和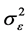 的无偏估计。
的无偏估计。
2.4.1. 第一步
从模型(1.4)的残差向量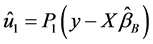 可以构造
可以构造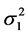 的一个无偏估计
的一个无偏估计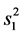
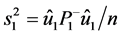 (1.6)
(1.6)
由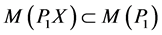 ,知
,知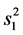 与广义逆
与广义逆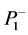 的选择无关。而引理1.1,
的选择无关。而引理1.1,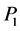 是对称幂等阵,因此它是自身的一个广义逆,(1.6)中的
是对称幂等阵,因此它是自身的一个广义逆,(1.6)中的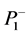 可简单地取为
可简单地取为 ,得
,得
 (1.7)
(1.7)
这里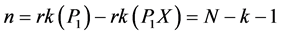 .易得
.易得 。
。
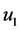 是正态分布,协方差阵为
是正态分布,协方差阵为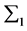 ,由于
,由于
 ,
,
即 和
和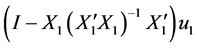 相互独立。而
相互独立。而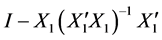 是对称幂等阵,所以
是对称幂等阵,所以
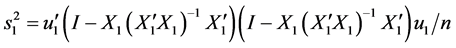
是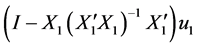 的函数,因此
的函数,因此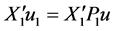 和
和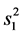 相互独立。
相互独立。
同样地,我们可以从模型(1.5)的残差向量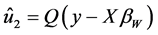 构造
构造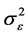 的一个无偏估计
的一个无偏估计
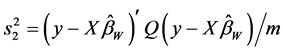 (1.8)
(1.8)
其中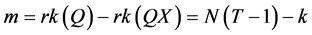 。
。 。并且
。并且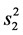 和
和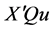 相互独立。
相互独立。
 ,
,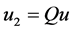 都是正态分布,同时
都是正态分布,同时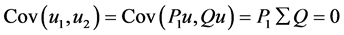 ,所以
,所以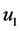 和
和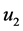 相互独立。
相互独立。 ,
,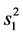 和
和 ,
,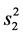 分别是
分别是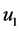 ,
,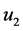 的函数,因此这两组是随机独立的。又有
的函数,因此这两组是随机独立的。又有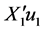 ,
,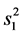 相互独立,
相互独立,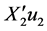 ,
,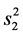 相互独立,所以
相互独立,所以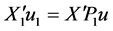 ,
,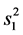 ,
,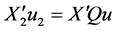 ,
,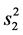 是相互独立的。这些结果可以写成下面的引理。
是相互独立的。这些结果可以写成下面的引理。
引理1.2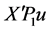 ,
, ,
,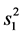 ,
,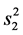 都相互独立。
都相互独立。
2.4.2. 第二步
将模型(1.4)和(1.5)联立,得到新的模型
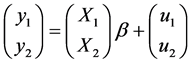
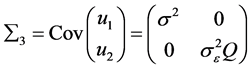
对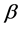 的估计来说,这个模型和模型(1.2)等价。模型(1.2)中
的估计来说,这个模型和模型(1.2)等价。模型(1.2)中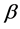 的最佳线性无偏估计为
的最佳线性无偏估计为
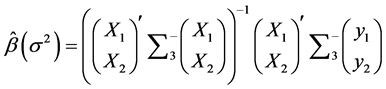 (1.9)
(1.9)
注意到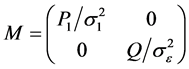 是
是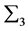 的一个广义逆,用M替换(1.9)中的
的一个广义逆,用M替换(1.9)中的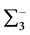 ,即可得到(1.3)式。利用
,即可得到(1.3)式。利用 和
和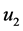 的独立性可以把BLU估计
的独立性可以把BLU估计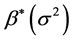 表示为
表示为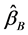 和
和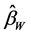 的以矩阵为权的凸组合形式
的以矩阵为权的凸组合形式
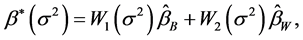
这里权矩阵
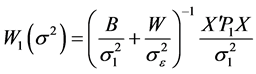 ,
,

 ,
,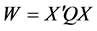 .
.
实际中,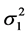 和
和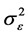 都未知,我们用它们的估计
都未知,我们用它们的估计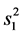 和
和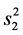 来代替。于是产生了
来代替。于是产生了 的一种两步估计
的一种两步估计
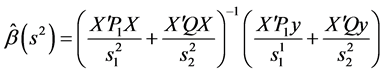
这里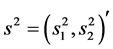 。显然
。显然
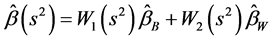
可证得两步估计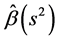 是
是 的无偏估计 [3] ,因为
的无偏估计 [3] ,因为
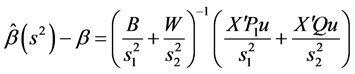
利用引理1.2可得
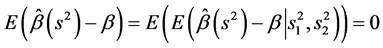
因此, 是
是 的无偏估计。
的无偏估计。
两步估计的协方差阵形式比较复杂,其证明过程也很繁琐,这里就不加讨论了。
3. 四种估计的比较
第一部分分别给出了Panel模型中回归系数的四种估计方法及其表达式,下面简要介绍一定条件下四种估计方法的优良性。
3.1. Pitman准则下估计的比较
Pitman于1937年提出的比较参数估计的准则被称为Pitman准则 [4] 。著名统计学家Rao [5] [6] 曾指出常用的均方误差准则的明显缺陷之一是过分强调以较小概率出现的那些大偏差,并且认为Pitman准则克服了这一明显缺陷,是评价估计优劣的更为本质的度量,之后Pitman受到了统计学家的广泛关注。下面首先给出其具体定义。
定义2.1 设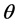 为未知参数向量,
为未知参数向量,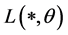 为损失函数,
为损失函数,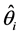 ,
, 为
为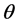 的两个估计,称
的两个估计,称
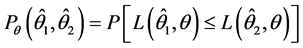 (2.1)
(2.1)
为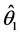 关于
关于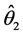 的Pitman度量。参数
的Pitman度量。参数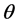 所有可能取值组成的集合称为参数空间
所有可能取值组成的集合称为参数空间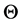 ,若对一切
,若对一切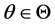 ,总有
,总有

成立,且至少对一个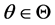 不等号成立,则称在Pitman意义下,
不等号成立,则称在Pitman意义下,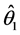 比
比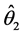 更接近于
更接近于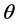 ,或称在Pitman意义下,
,或称在Pitman意义下,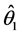 优于
优于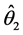 。这里取二次损失函数
。这里取二次损失函数 。有如下结论:
。有如下结论:
1) 当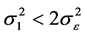 ,在Pitman准则下LS估计优于Within估计,这里损失函数
,在Pitman准则下LS估计优于Within估计,这里损失函数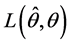 中的
中的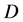 取
取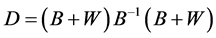
2) 在Pitman准则下LS估计优于Between估计,这里损失函数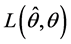 中的
中的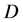 取为
取为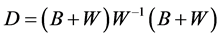 。
。
3.2. 广义均方误差意义下两步估计的优良性
定义2.2 设参数向量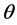 的一个估计为
的一个估计为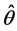 ,则
,则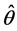 的广义均方误差(GMSE)定义为
的广义均方误差(GMSE)定义为
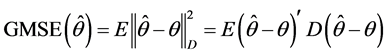
本节取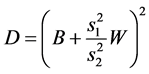
记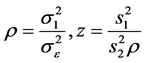 ,易见
,易见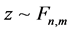 。有如下结论:
。有如下结论:
1) 当 时,在广义均方误差意义下两步估计优于Between估计。
时,在广义均方误差意义下两步估计优于Between估计。
2) 若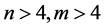 则两步估计
则两步估计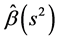 优于
优于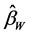 的充分条件是
的充分条件是
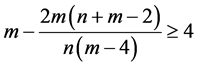 ,
,
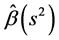 优于
优于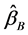 的充分条件是
的充分条件是
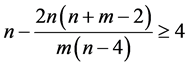 ,这里
,这里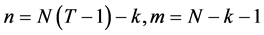
我们可以认为,当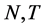 较大时,两步估计要优于Within估计和Between估计。
较大时,两步估计要优于Within估计和Between估计。
文章引用
康文倩. 浅谈Panel模型中未知参数的四种估计方法
Four Methods for Estimating Unknown Parameters in Panel Model[J]. 统计学与应用, 2017, 06(01): 92-97. http://dx.doi.org/10.12677/SA.2017.61010
参考文献 (References)
- 1. 王松桂, 史建红, 尹素菊, 吴密霞. 线性模型引论[M]. 北京: 科学出版社, 2004.
- 2. 王松桂, 范永辉. Panel模型中两步估计的优良性[J]. 应用概率统计, 1998, 14(2): 177-184.
- 3. 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 北京: 高等教育出版社, 2006.
- 4. Pitman, E. (1937) The Closest Estimates of Statistical Parameters. Proceedings of the Cambridge Philosophical Society, 33, 212-222. https://doi.org/10.1017/S0305004100019563
- 5. Rao, C.R. (1981) Some Comments the Minimum Mean Square as Criterion of Estimation. Statistics and Related To- pics, North Holland, Amsterdam, 123-143.
- 6. Rao, C.R., Keating, J.P. and Mason, R.L. (1986) The Pitman Nearness Criterion and Determination. Communications in Statistics-Theory and Methods, 15, 3173-3191. https://doi.org/10.1080/03610928608829302