Statistical and Application
Vol.04 No.04(2015), Article ID:16725,13
pages
10.12677/SA.2015.44037
A Jump-Preserving Curve Regression Procedure Based on Bilateral Kernel Estimation
Yiran Li, Xingfang Huang*, Jiazhao Ding, Xuan Chen
Department of Mathematics, Southeast University, Nanjing Jiangsu

Received: Dec. 10th, 2015; accepted: Dec. 28th, 2015; published: Dec. 31st, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
It is well known that curve regression is very important in many applications. However, since data collection procedures are disturbed by errors, traditional curve regression methods cannot play well in jump points. This paper proposes a jump-preserving curve fitting procedure, which is based on bilateral kernel estimation. Kernel functions are not only added to x-axis, but also added to y-axis. Then, we estimate given points from left side, right side and whole neighborhood. Weighted residual sums of squares are calculated to compare. The estimate with smaller weighted residual sums of squares is selected as the final estimate of the given point, so that we can achieve jump- preserving while not to detect jump points at first. Numerical simulation and real data analysis demonstrate the feasibility and efficiency of this method.
Keywords:Curve Fitting Procedure, Jump-Preserving, Bilateral Kernel Estimation, Weighted Residual Sums of Squares, Discontinuous Curve

基于双边核估计的保持跳跃曲线回归过程
李怡然,黄性芳*,丁嘉沼,陈旋
东南大学数学系,江苏 南京

收稿日期:2015年12月10日;录用日期:2015年12月28日;发布日期:2015年12月31日

摘 要
跳跃曲线回归在某些实际问题中非常重要,但是由于数据采集过程中受到噪声的干扰,传统的曲线回归方法对于跳跃位置的保持效果欠佳。本文基于分段双边核估计提出了一个保持跳跃的曲线拟合过程。该过程不仅在x方向上用核函数进行加权,亦在y方向上使用核函数。在目标点的邻域内,分别在左半邻域、右半邻域和全邻域对函数进行估计,并计算加权残差平方和以进行比较,选取较小的加权残差平方和的一个作为目标点的最终估计,以此来达到无需提前探测跳跃点的同时保持曲线跳跃特性的目的。数值模拟和实际数据分析表明该方法的可行性和有效性。
关键词 :曲线拟合,保持跳跃,双边核估计,加权残差平方和,不连续曲线

1. 引言
曲线回归,即找出两个变量间数量变化的函数关系,在实际问题中应用广泛。通过数据找出一个回归函数会比直接分析原始数据更加简单、方便,因为原始数据通常数量巨大,且有噪声干扰,无法很好的反应总体特征。在一些应用中,用带有跳跃的回归模型比光滑的回归模型对数据有更好的描述。比如,尽管一个国家的人口随时间基本稳定增长,在发生大规模战争或者移民的情况下人口总数会有暴跌或者激增。江河的流量是基本稳定的,但若上流有大坝蓄水,则在下游测量流量时,会大幅下降,而到蓄水结束时,流量在短时间内有会大幅上升。在这些情况下,如果还用传统不带跳跃的模型拟合,则会产生较大误差;带跳跃的曲线拟合会更好地处理数据不连续变化的情况。本文提出一个可行的、保持跳跃的曲线拟合方法。
众所周知,传统的局部线性核估计,在目标点的邻域中使用所有数值进行拟合,若待估点为连续点,则有很好的保持光滑的性质。当目标点存在跳跃时,传统的局部线性核估计不再具有统计相合性。在文献中,已有间接的方法来处理这个问题,即先探测出不连续的位置,再在其左右区间分别使用传统估计方法进行估计。探测跳跃的方法有:单边常数核光滑 (Müller 1992 [1] , Qiu et al. 1991 [2] , Wu and Chu 1993 [3] );单边线性核光滑(Loader 1996 [4] );局部最小二乘估计(Qiu and Yandell 1998 [5] );小波变换(Wang 1995 [6] );半参模型(Eubank andSpeckman 1994 [7] )和平滑样条建模(Koo 1997 [8] , Shiau et al. 1986 [9] )。与这些间接方法对比,直接方法不需要先探测跳跃点的位置,在估计区间内,把每一点都当做可能的跳跃点,用相同的方法进行估计。McDonald和Owen (1986) [10] 提出了基于三个局部最小二乘估计的曲线回归方法,分别对应一给定点的左边估计、右边估计和两边估计。他们通过对这三个估计加权平均,建立了“分离线性拟合”,权重由各个估计的拟合优度决定。Qiu (2003) [11] 提出了一个基于局部分段线性核估计的保持跳跃的曲线拟合过程。对每个点x,分别考虑两边的局部线性估计,并计算加权残差平方和以作比较。将加权残差平方较小的估计作为x最后的估计,若两个值基本相等,则取平均作为x最后的估计。此方法可以保持曲线的光滑性,并在跳跃处也有较好拟合效果。
本文基于局部分段的双边核估计过程,提出一个用于保持跳跃的曲线拟合方法。该方法使用较少的迭代次数,自适应的保持跳跃的特征,并且在非跳跃处有较好的光滑性。本方法的特点是在估计的过程中不但考虑自变量的加权函数,同时对因变量进行加权。把每个点都看作是可能的跳跃点,分别在左邻域、右邻域和整个邻域内分别进行估计,选择加权残差平方和较小的估计作为估计处最终的估计。
本文结构如下:第二部分介绍了跳跃回归模型;详细的算法在第三部分介绍;第四部分展示了数值模拟结果和一个实例分析;最后,就本文的结果和存在的问题进行了讨论。
2. 跳跃回归模型
给定一组观测数据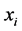 ,
,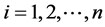 带有跳跃的回归模型定义如下:
带有跳跃的回归模型定义如下:
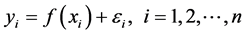 (1)
(1)
其中,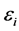 是随机产生的、独立同分布的噪声,均值为0,方差是
是随机产生的、独立同分布的噪声,均值为0,方差是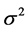 。不失一般性,
。不失一般性,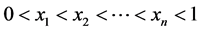 是观测点,
是观测点,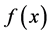 是回归函数,在[0,1]上连续,
是回归函数,在[0,1]上连续, 是跳跃点,跳跃的大小为
是跳跃点,跳跃的大小为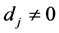 ,
,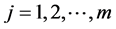 。
。
在文献中,已有几种对上述跳跃模型的保跳拟合过程。其中一个是Fan, J.和Gijbels, I. [12] 在1996年提出的最小化问题:
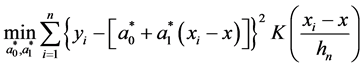 (2)
(2)
其中, 是定义在
是定义在 上的核函数,
上的核函数,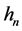 是带宽参数。(2)式的解被定义为
是带宽参数。(2)式的解被定义为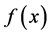 的局部线性核估计。
的局部线性核估计。
这个曲线拟合过程会在跳跃处表现出“模糊”,即跳跃无法保持的很好。因此,我们希望得到一个保持跳跃的曲线拟合过程,同时有一个相对较高的收敛速度。
3. 基于双边核的保跳曲线拟合过程
基于在第二部分定义的模型,我们定义一个新的最小化过程:
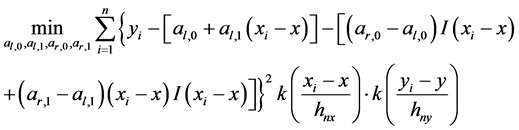 (3)
(3)
来拟合曲线。
其中,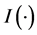 是示性函数,
是示性函数,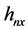 是x方向的带宽,
是x方向的带宽,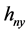 是y方向的带宽。
是y方向的带宽。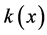 是核函数 [13] ,核函数是一个非负的、实值可积分函数,有如下性质:
是核函数 [13] ,核函数是一个非负的、实值可积分函数,有如下性质:
1) ;
;
2)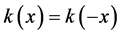 。
。
这里,我们介绍双边核函数。传统局部线性估计方法是用一个核函数在x邻域内进行加权。双边核
不仅考虑x方向上的权重,也在y方向上用核函数对数据点加权。我们定义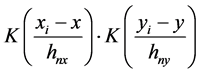 为双边加权函数,即双边核函数。
为双边加权函数,即双边核函数。
我们注意到最小化过程(3)等价于以下两个最小化过程的和:
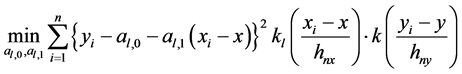 (4)
(4)
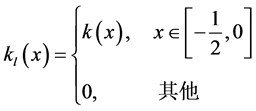
和
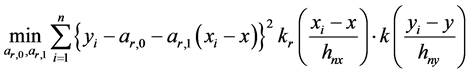 (5)
(5)
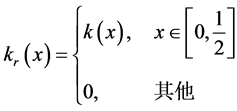
在本文的算法中,核函数形式的选取对结果的影响不明显,即不同的核函数不会影响建模和算法的实际应用。在本文的数值模拟和实例中,我们在x方向和y方向上均使用Epanechnikov核函数

最小化过程(4)、(5)分别在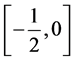 和
和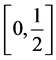 上对
上对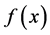 进行估计。为求解这两个问题,我们记:
进行估计。为求解这两个问题,我们记: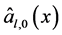 ,
,
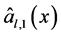 ,
,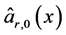 ,
,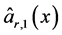 :
:
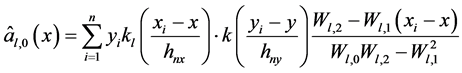 (6)
(6)
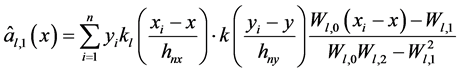 (7)
(7)
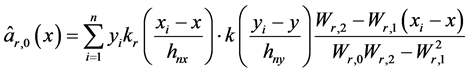 (8)
(8)
 (9)
(9)
其中,
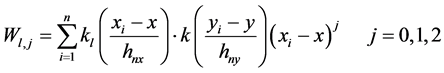 (10)
(10)
 (11)
(11)
这样,根据线性回归的定义,我们知道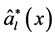 和
和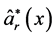 是
是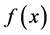 的两个估计,分别记作:
的两个估计,分别记作:
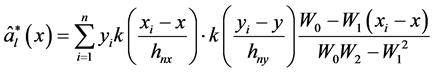 (12)
(12)
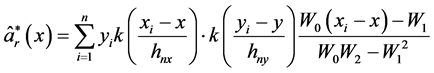 (13)
(13)
其中,
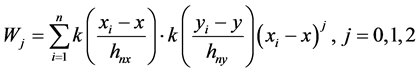 (14)
(14)
和全邻域估计:
 (15)
(15)
另,全邻域估计量:
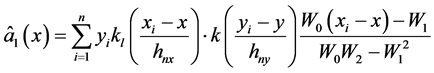 (16)
(16)
下一步,我们分别计算两边的加权残差平方和:
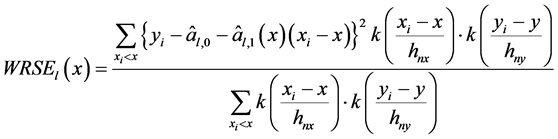 (17)
(17)
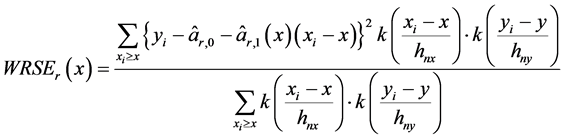 (18)
(18)
 (19)
(19)
并记:
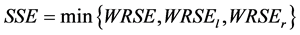 , (20)
, (20)
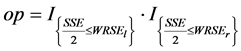 , (21)
, (21)
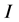 为示性函数,下标条件成立时取值为1;否则为0。
为示性函数,下标条件成立时取值为1;否则为0。
并定义:
 (22)
(22)
作为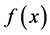 的估计,
的估计,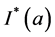 是示性函数,
是示性函数,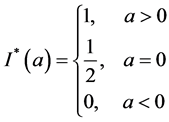 。
。
另外,带宽的选取在非参数统计中是一个非常重要的问题。常用的带宽选取方法有大拇指准则、交叉验证法等。Silverman [14] 大拇指准则选取带宽的方法为
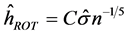
这里的C为常数,可供备选的常数有1.06或3或5,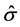 为样本标准差的估计,n为样本数。大拇指准则选取带宽有简便实用的特点。交叉验证法选取带宽的方法为最小化下面的式子以获得最优带宽
为样本标准差的估计,n为样本数。大拇指准则选取带宽有简便实用的特点。交叉验证法选取带宽的方法为最小化下面的式子以获得最优带宽
 (23)
(23)
这里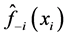 指的是去掉第i组观测值后用本文方法在带宽
指的是去掉第i组观测值后用本文方法在带宽 下得到估计值。
下得到估计值。
本文在双边核的保跳曲线拟合过程中加入迭代,以增强算法的有效性。适当的迭代可使拟合效果更佳,而过多的迭代次数会使数据连续部分细节损失。根据每次迭代后加权残差平方和变化的大小设定一个阈值,可有效控制迭代次数,得到更佳的拟合效果。
4. 数值实验
4.1. 仿真模拟
在模拟仿真中,我们将比较包括局部分段线性双边核估计在内的四种方法的估计效果,通过对比说明我们提出方法的有效性和优越性。模拟实验过程如下:
等间隔的选取设计点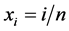 ,从模型
,从模型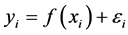 ,
,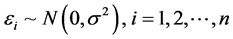 中产生观测值
中产生观测值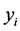 。其中
。其中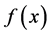 为真实的密度函数,我们将计算NW核估计、局部线性核估计、局部分段线性核估计和本文的局部分段双边核估计。
为真实的密度函数,我们将计算NW核估计、局部线性核估计、局部分段线性核估计和本文的局部分段双边核估计。
前两种估计为常见的传统非参数核估计方法,对于光滑的真实密度函数 [15] 有较好的估计效果,而在跳跃点处不具有一致相合性。Qiu [16] 提出的局部分段线性核估计有较好的保跳性质,它将作为我们主要的对比对象。在下面的数值模拟中可以看出,本文提出的局部分段线性双边核估计较之有更好的效果。
选定数据点数n=100,噪声标准差为0.1。大拇指准则选取x方向的带宽乘数为1.06。为了减小结果中随机性的影响,以下算得的MSE值均为重复100次取平均值的结果。“BK-rot”指大拇指准则选取带宽下双边核算得的MSE值,“SK-rot”指大拇指准则选取带宽下单边核算得的MSE值,“LLR”指大拇指准则选取带宽下传统局部线性方法算得的MSE值,“NW”指大拇指准则选取带宽下NW核估计算得的MSE值。这里的LLR和NW方法不参与迭代。
选定真实密度函数为
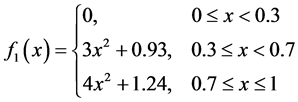
原始函数图像如图1。大拇指准则中选取y方向的带宽乘数设为3。给定迭代终止的阈值为0.0005。如图2所示,红色实线代表真实密度曲线,绿色实点表示观测值,黑色实线为局部分段线性双边核估计曲线,紫色点划线为局
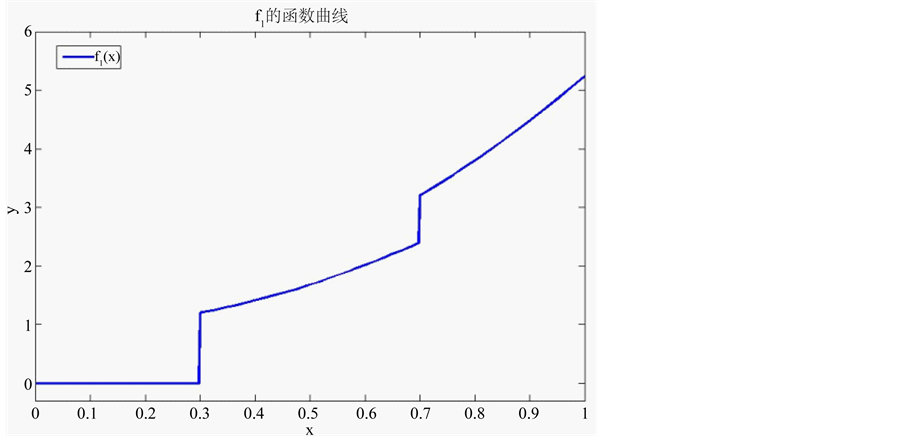
Figure 1. Original image of f1(x)
图1. f1(x)的原始函数图像
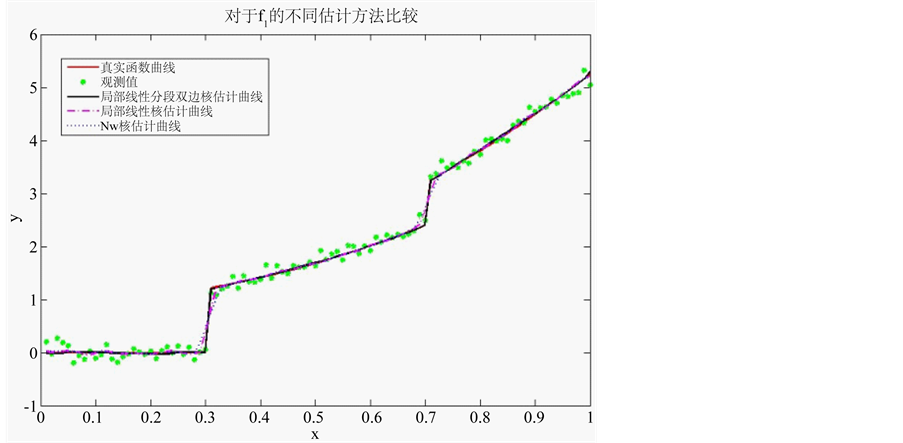
Figure 2. Comparison among different estimation methods of f1(x)
图2. 对f1(x)不同估计方法的比较
部线性核估计曲线,点线表示NW核估计得到的曲线。图3中黑色实线表示局部分段线性双边核估计,两条虚线分别代表97.5%分位数曲线和2.5%分位数曲线。
显然,NW核估计和局部线性核估计不能保持真实密度函数在跳跃点处的跳跃特性。而局部分段线性双边核估计能较好的保持真实密度函数的跳跃特征。下面从MSE数值的角度对局部分段线性双边核估计和局部分段线性单边核估计的效果进行分析。可以看出给定迭代次数,双边核估计均优于单边核估计,说明本文提出方法的有效性。
表1和图4给出了不同迭代次数下局部分段线性双边核估计的MSE结果。从迭代次数与MSE值得关系可以看出,适当的迭代的确会使估计效果更佳。值得注意的是,过多的迭代次数会使MSE值增大,
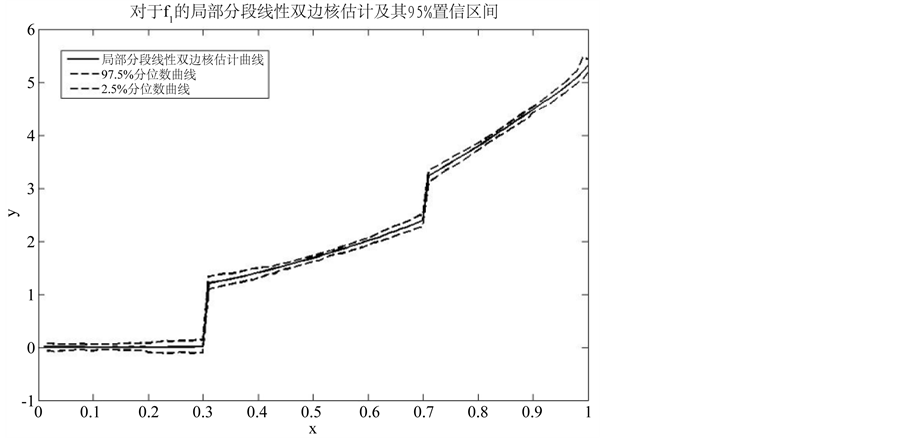
Figure 3. Confidence interval of f1(x)
图3. f1(x)置信区间
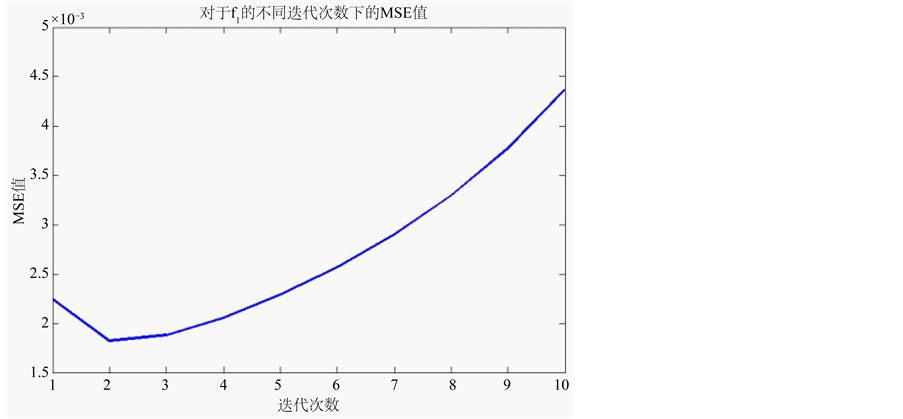
Figure 4. f1(x) MSE of local piecewise linear bilateral Kernel estimation under different iteration times
图4. f1(x)不同迭代次数下局部分段线性双边核估计的MSE值
Table 1. MSE value for different estimation method of f1(x)
表1. f1(x)不同估计方法对应的MSE值
这是因为数据连续部分细节损失造成的。
下面,改变真实密度函数为
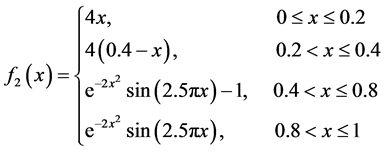
原始函数图像如图5所示。
大拇指准则中选取y方向的带宽乘数设为5。给定迭代终止的阈值为0.0005。如图6所示,红色实线代表真实密度曲线,绿色实点表示观测值,黑色实线表示局部分段线性双边核估计,紫色点划线表示局部线性核估计,点线表示NW核估计得到的曲线。图7中黑色实线表示局部分段线性双边核估计,两条虚线分别代表97.5%分位数曲线和2.5%分位数曲线。
类似的,NW核估计与局部线性核估计在跳跃点处的偏差较大。而局部分段线性双边核估计能较好保持原始数据的跳跃特征。从表2中可以看出给定迭代次数,局部分段线性双边核估计的MSE值均小于局部分段线性单边核估计的MSE值,说明本文提出的方法估计效果更佳。
如图8所示,局部分段线性核估计中MSE值与迭代次数的关系与前例相似。
综上所述:传统的核光滑回归估计方法对带有跳跃点的回归曲线估计效果较差。大拇指准则选取的带宽下,相比于传统的局部分段单边核线性估计,双边核得到估计效果更佳。在迭代次数的选择问题上,数值实验演示,2~5次迭代的确可以改善估计效果,在实际应用中灵活选取。
4.2. 数值实例
下面,我们将本文提出的方法应用于一个股票数据。我们从yahoo.finance [17] 收集了中国东方航空公司在纽约证券所从2014年8月8日至2015年11月9日连续67周股价的周末收盘价。图9中的红色实点表示连续67周中国东方航空公司的周末收盘价。需要注意的是,我们将67个数据进行了标准化预处理。

Figure 5. Original image of f2(x)
图5. f2(x)的原始函数图像
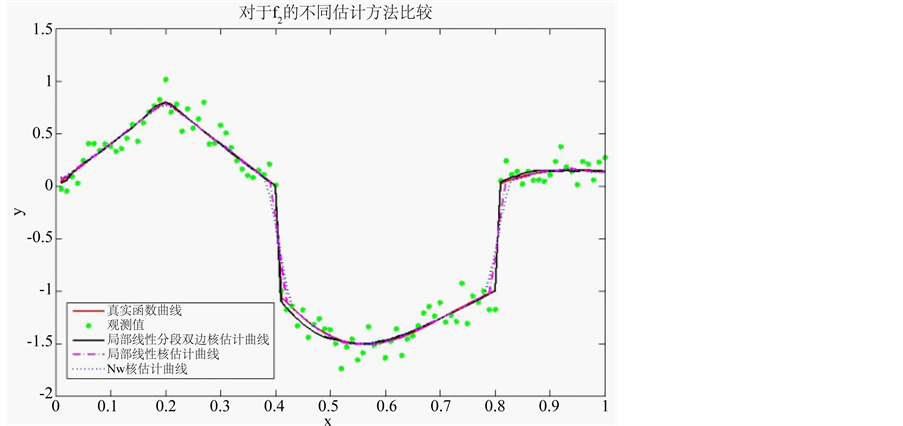
Figure 6. Comparison among different estimation methods of f2(x)
图6. 对f2(x)不同估计方法的比较
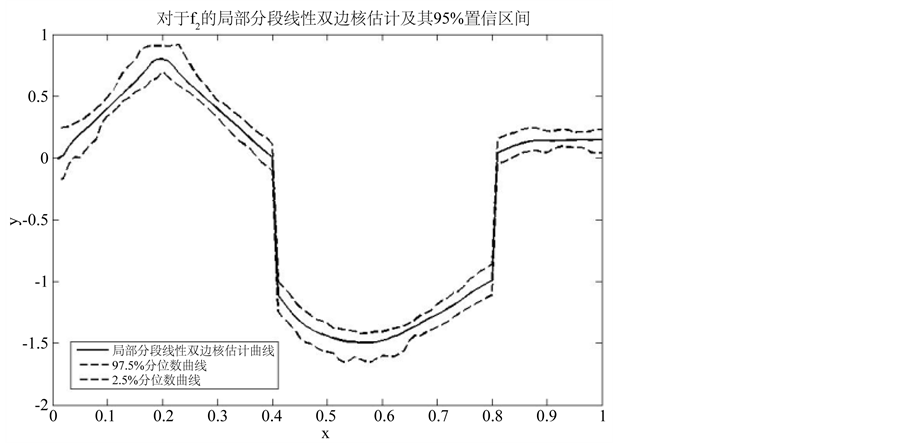
Figure 7. Confidence Interval of f2(x)
图7. f2(x)置信区间
Table 2. MSE value for different estimation method of f2(x)
表2. f2(x)不同估计方法对应的MSE值

Figure 8. f2(x) MSE of local piecewise linear bilateral Kernel estimation under different iteration times
图8. f2(x)不同迭代次数下局部分段线性双边核估计的MSE值
图9中右图的黑色实线是本文局部分段线性双边核估计方法得到的回归曲线,红色实点表示中国东方航空公司连续67周的周末收盘价。蓝色实线为周末收盘价的变化情况。黑色实线为局部分段线性双边核估计得到的回归曲线,在该方法中进行了4次迭代。从图上可以看出,在第35个点和第52个点处发生了跳跃,分别是2015年8月24日和2015年4月6号。关于8月的下跌(即跳跃),2015年8月17日新闻报道中国东方航空36.3亿美元购15架A330飞机,然而8月人民币遭受了近20年来最大的贬值,同时中国的经济指数暗示经济增长放缓,人们担心中国东方航空将会花费比预计更多的人民币来购买这些新飞机,成为其股价下跌的可能因素。在2015年4月,美国达美航空与东航合作,在上海建立国际中心,意欲打造国际枢纽;4月22日,中国东方航空公布2014财年报告,这些都是利好消息,可能是其股价激增的原因。综上,本文方法能够在去噪的同时保持曲线的跳跃特征,有利于更进一步的统计推断。
5. 讨论
5.1. 光滑性
本文提出的算法在连续区间上可以保持光滑性。这是因为需拟合的函数连续时,给定点左邻域的估计和右邻域的估计是近似相等的。由定义(19)可知,此时 的估计是左邻域估计和右邻域估计的平均,因此保证了连续区间内的光滑性。
的估计是左邻域估计和右邻域估计的平均,因此保证了连续区间内的光滑性。
5.2. 带宽选择
在带宽的选取上,使用大拇指准则。大拇指准则是一种数据驱动的带宽选取方法,操作简便,不受估计方法的影响。本文提出的方法的重要创新点在于保跳回归估计中加入因变量y的影响。显然,跳跃点附近的y值变化剧烈,而引入了y的核函数后可以描述y值的性质。在回归函数的连续区域,y值平稳变化,y方向的核函数与x方向的核函数相互配合,进行平滑的估计;而在跳跃点的左右两侧中一侧的y方向的核函数对另一侧估计的权重很小,因此可以达到刻画函数跳跃性质的目的。这时涉及到y的带宽选取问题, 我们建议采用乘数为3或5的大拇指准则来自适应的选取y的带宽,其值应根据具体样本选取,此问题需进一步研究 [18] 。应当注意,原始函数的特点对估计效果有一定的影响。本文方法对原始函数是近

Figure 9. Real data image and its fitting result
图9. 数值实例图像及其拟合结果
似于含有第一类跳跃点的单调函数的估计效果更好。
5.3. 迭代次数
模拟仿真研究中,我们发现回归曲线的拟合受迭代次数的影响,适当的迭代可使拟合效果更佳。而过多的迭代次数却会使拟合效果变差,原因在于过多的迭代使得回归函数在连续的地方退化成一条直线。因此选取恰当的迭代次数在一定程度上会使保跳性得到更好的实现,同时保持连续区域的光滑性。最佳的迭代次数还需要进一步的研究,推荐迭代次数为2-5次。如何使迭代发挥出最佳效果需要继续深入研究。
致谢
本文是在东南大学数学系林金官老师细心指导和建议下完成,在此对林金官老师表示衷心的感谢!
基金项目
本文获得国家自然科学基金项目(11401094)和教育部人文社会科学青年基金项目(13YJC910006)资助。
文章引用
李怡然,黄性芳,丁嘉沼,陈旋. 基于双边核估计的保持跳跃曲线回归过程
A Jump-Preserving Curve Regression Procedure Based on Bilateral Kernel Estimation[J]. 统计学与应用, 2015, 04(04): 335-347. http://dx.doi.org/10.12677/SA.2015.44037
参考文献 (References)
- 1. Müller, H.-G. (1992) Change-Points in Nonparametric Regression Analysis. The Annuals of Statistics, 20, 737-761. http://dx.doi.org/10.1214/aos/1176348654
- 2. Qiu, P., Cho, A. and Li, X. (1991) Estimation of Jump Regression Functions. Bulletin of Information and Cybernetics, 24, 197-212.
- 3. Wu, J.S. and Chu, C.K. (1993) Kernel Type Es-timators of Jump Points and Values of a Regression Function. The Annals of Statistics, 21, 1545-1566. http://dx.doi.org/10.1214/aos/1176349271
- 4. Loader, C.R. (1996) Change Point Estimation Using Nonparametric Regression. The Annals of Statistics, 24, 1667- 1678. http://dx.doi.org/10.1214/aos/1032298290
- 5. Qiu, P. and Yandell, B.(1998) A Local Polynomial Jump Detection Algorithm in Nonparametric Regression. Technometrics, 40, 141-152.
- 6. Wang, Y. (1995) Jump and Sharp Cusp Detection by Wavelets. Biometrika, 82, 385-397. http://dx.doi.org/10.1093/biomet/82.2.385
- 7. Eubank, R.L. and Speckman, P.L. (1994) Nonparametric Estimation of Functions with Jump Discontinuities. In: Carlstein, E., Müller, H.G. and Siegmund, D., Eds., IMS Lecture Notes, Vol. 23, Change-Point Problems, 130-144. http://dx.doi.org/10.1214/lnms/1215463119
- 8. Koo, J.Y. (1997) Spline Estimation of Discontinuous Regression Functions. Journal of Computational and Graphical Statistics, 6, 266-284.
- 9. Shiau, J.H., Wahba, G. and Johnson, D.R. (1986) Partial Spline Models for the Inclusion of Tropopause and Frontal Boundary Information in Otherwise Smooth Two- and Three-Dimensional Objective Analysis. Journal of Atmospheric and Oceanic Technology, 3, 714-725. http://dx.doi.org/10.1175/1520-0426(1986)003<0714:PSMFTI>2.0.CO;2
- 10. McDonald, J.A. and Owen, A.B. (1986) Smoothing with Split Linear Fits. Technometrics, 28, 195-208. http://dx.doi.org/10.1080/00401706.1986.10488127
- 11. Qiu, P. (2003) A Jump-Preserving Curve Fitting Proce-dure Based on Local Piecewise-Linear Kernel Estimation. Jour- nal of Nonparametric Statistics, 15, 437-453. http://dx.doi.org/10.1080/10485250310001595083
- 12. Fan, J. and Gijbels, I. (1996) Local Polynomial Modeling and Its Applications. Chapman & Hall, London, 66.
- 13. Wikipedia, Kernel (Statistics). https://en.wikipedia.org/wiki/Kernel_(statistics)
- 14. Silverman, B.W. (1986) Density Estimation for Statistics and Data Analysis. Chapman & Hall, London, 39, 296-297. http://dx.doi.org/10.1007/978-1-4899-3324-9
- 15. Nadaraya, E.A. (1964) On Estimating Regression. Theory of Probability & Its Applications, 9, 141-142. http://dx.doi.org/10.1137/1109020
- 16. Qiu, P. (1994) Estimation of the Number of Jumps of the Jump Regression Functions. Communications in Statistics-Theory and Methods, 23, 2141-2155. http://dx.doi.org/10.1080/03610929408831378
- 17. Finance.yahoo.com. CEA Weekly-Adjusted Close Price. http://finance.yahoo.com/q/hp?s=CEA+Historical+Prices
- 18. Loader, C.R. (1999) Bandwidth Selection: Classical or Plug-In? Annals of Statistics, 27, 415-438. http://dx.doi.org/10.1214/aos/1018031201
NOTES
*通讯作者。
