Pure Mathematics
Vol.05 No.04(2015), Article ID:15619,6
pages
10.12677/PM.2015.54020
A New Semi-Topological Space and Its Separation Property
Xichao Hu, Peiyong Zhu
School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu Sichuan
Email: 540435650@qq.com, zpy6940@uestc.edu.cn
Received: Jun. 18th, 2015; accepted: Jul. 1st, 2015; published: Jul. 8th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In 2002, the concept of a generalized topological space was introduced by A. Csaszar. But it contains only half of the conditions in the definition of a topological space. Therefore, a generalized topology is a kind of semi-topologies actually. If we use the other condition of a topology which is contrary to the generalized topology as another semi-topology, can this new semi-topology be of some good properties, just like a generalized topology? This thesis is about this problem, and several results are obtained for the theories of point set and separation properties of this semi-topological space.
Keywords:Generalized Topology (Sup-Semi-Topology), Inf-Semi-Topology, Separation Property
一类新型半拓扑空间及其分离性质
胡西超,朱培勇
电子科技大学数学科学学院,四川 成都
Email: 540435650@qq.com, zpy6940@uestc.edu.cn
收稿日期:2015年6月18日;录用日期:2015年7月1日;发布日期:2015年7月8日

摘 要
2002年,A. Csaszar引入的广义拓扑空间定义仅包含拓扑空间定义条件的一半。因此,广义拓扑实际上是一类半拓扑。如果把广义拓扑相对于拓扑的另一半条件作为另一类半拓扑,那么这类半拓扑能否像广义拓扑那样具有一些良好的特征性质?本文就此问题进行研究,在这类半拓扑的点集理论和分离性质获得了一系列结果。
关键词 :广义拓扑(上半拓扑),下半拓扑,分离性

1. 引言与预备知识
广义拓扑空间的概念由匈牙利数学家A. Csaszar于2002在文献[1] 中引入。近些年来,不少学者积极投入,取得了不少的研究成果(参见文献[1] -[7] 等)。然而,广义拓扑定义中条件仅是拓扑定义中条件的一半,即广义拓扑实际上是一类半拓扑。在此,下列问题自然被提出:
问题1:如果把广义拓扑相对于拓扑的另一半条件作为另一类半拓扑,那么这类半拓扑能否像广义拓扑那样可以进行研究?
本文首先引入上述半拓扑(称为下半拓扑)及其相关的点集概念;然后,类比拓扑空间的点集理论,讨论下半拓扑空间对拓扑空间中的一系列点集性质的保持性;最后,引入下半拓扑空间的分离性质,得到了与拓扑空间的分离性质相同和相异的一系列结果。
首先,回忆广义拓扑的概念:
定义1.1 [8] :设 是任一非空集合,
是任一非空集合, 是
是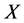 的一些子集构成的集族,如果下列两个条件被满足:(GO1)
的一些子集构成的集族,如果下列两个条件被满足:(GO1) ;(GO2)若
;(GO2)若
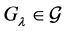 ,其中
,其中 为任意指标集,则
为任意指标集,则 。则称
。则称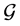 为集合
为集合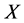 上的一个广义拓扑,并且称有序偶
上的一个广义拓扑,并且称有序偶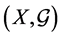 为一个广义拓扑空间,集族
为一个广义拓扑空间,集族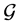 中的每一个集合都称为广义拓扑空间
中的每一个集合都称为广义拓扑空间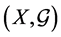 的广义开集。
的广义开集。
不难看出:广义拓扑的条件只有拓扑条件的一半。因此,广义拓扑实际上就是一个半拓扑。为了引入新的半拓扑,本文也称广义拓扑为上半拓扑(Sup-semi-topology),新引入的半拓扑称为下半拓扑(Inf-semi-topology),如下:
定义1.2:设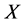 是任一非空集合,
是任一非空集合,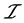 是
是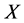 的一些子集构成的集族,如果下列两个条件被满足:(IO1)
的一些子集构成的集族,如果下列两个条件被满足:(IO1)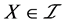 ;(IO2)若
;(IO2)若 ,则
,则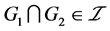 。则称
。则称 为
为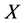 上的一个下半拓扑(Inf-semi-topology),并称
上的一个下半拓扑(Inf-semi-topology),并称 为下半拓扑空间(Inf-semi-topological space),简记为ISTS。集族
为下半拓扑空间(Inf-semi-topological space),简记为ISTS。集族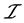 中的每一个元都称为
中的每一个元都称为 中的下半开集。下半开集的余集称为下半闭集。
中的下半开集。下半开集的余集称为下半闭集。
显然,下一结论是不证自明的:
定理1.1:设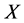 是任一非空集合,则
是任一非空集合,则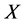 的一些子集构成的集族
的一些子集构成的集族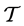 是
是 上的一个拓扑当且仅当
上的一个拓扑当且仅当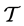 既是
既是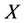 上的广义拓扑(上半拓扑)又是
上的广义拓扑(上半拓扑)又是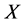 上的下半拓扑。
上的下半拓扑。
根据定理1.1,下面问题自然被提出:
问题2:在一般拓扑学中,拓扑的哪些是由上半拓扑导出的,哪些又是由下半拓扑导出的呢?
本文就此问题展开讨论。首先,对下半拓扑引入如下相关概念:
定义1.3:设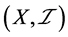 是一个ISTS,
是一个ISTS, 称为是
称为是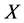 上的一个强下半拓扑,如果
上的一个强下半拓扑,如果 。这时也称下半拓扑空间
。这时也称下半拓扑空间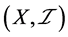 为强下半拓扑空间,简记为S-ISTS。
为强下半拓扑空间,简记为S-ISTS。
从上面的定义可以看出,强下半拓扑空间是一类特殊的下半拓扑空间。
定义1.4:设 是一个ISTS,
是一个ISTS, ,
, ,如果
,如果 使得
使得 ,则称
,则称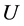 为点
为点 的一个下半邻域。点
的一个下半邻域。点 的下半邻域的全体称为
的下半邻域的全体称为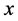 的下半邻域系,记为
的下半邻域系,记为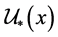 。
。
定义1.5:设 是一个ISTS,
是一个ISTS,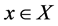 ,
,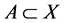 ,若
,若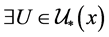 使得
使得 ,则称
,则称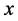 为点集
为点集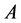 的下半内点;点集
的下半内点;点集 的下半内点的全体称为
的下半内点的全体称为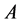 的下半内部,记为
的下半内部,记为 。
。
定义1.6:设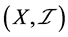 是一个ISTS,
是一个ISTS,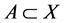 ,
,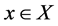 ,如果
,如果 ,有
,有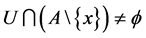 ,则称
,则称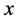 为点集
为点集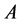 的下半聚点;点集
的下半聚点;点集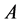 的下半聚点的全体称为
的下半聚点的全体称为 的下半导集,记为
的下半导集,记为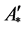 ;记
;记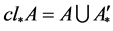 ,并称
,并称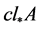 为
为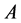 的下半闭包。
的下半闭包。
定义1.7:设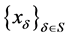 是下半拓扑空间
是下半拓扑空间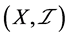 中的一个网,
中的一个网, ,若
,若 ,
, ,使得
,使得 ,当
,当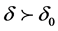 时,恒有
时,恒有 ,则称网
,则称网 (按下半拓扑
(按下半拓扑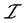 )收敛于
)收敛于 或称
或称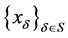 以
以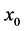 为下半极限,通常记为
为下半极限,通常记为 或
或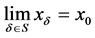 。
。
类比拓扑空间的分离性质,在下半拓扑中引入IS-分离性质如下:
定义1.8:设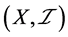 是一个ISTS。
是一个ISTS。
(1) 称 为
为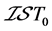 空间,如果
空间,如果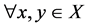 ,若
,若 ,则
,则 ,使得
,使得 ,或者
,或者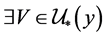 使得
使得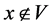 ;
;
(2) 称 为
为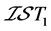 空间,如果
空间,如果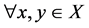 ,若
,若 ,则
,则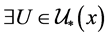 ,
,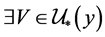 ,使得
,使得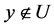 并且
并且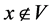 。
。
定义1.9:设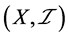 是一个S-ISTS。
是一个S-ISTS。
(1) 称 为
为 空间,如果
空间,如果 ,若
,若 ,则
,则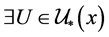 ,
, ,使得
,使得 ;
;
(2) 称 为
为 -正则空间,如果对
-正则空间,如果对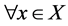 ,
, 下半闭于
下半闭于 且
且 ,则
,则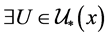 ,
, ,使得
,使得 ;
;
(3) 称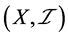 为
为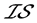 -正规空间,如果
-正规空间,如果 下半闭于
下半闭于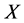 且
且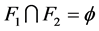 ,则
,则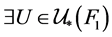 ,
, ,使得
,使得 。
。
此外,本文中所有没定义的关于拓扑空间的概念、术语和记号,如果没有特殊声明都选自文献[9] 。在不引起混淆的情况下,本文也将下半开集、下半闭集、下半闭包等称为开集、闭集、闭包等。
2. 下半拓扑空中基本点集性质
命题2.1:设 是一个ISTS,
是一个ISTS, ,
, ,则:
,则:
(1) 若 为
为 中的开集,则
中的开集,则 ;
;
(2) 若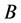 是
是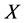 中的闭集,则
中的闭集,则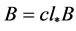 。
。
证明:(1) 由内部的定义得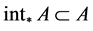 ,下证
,下证 。事实上,
。事实上, ,由
,由 ,故
,故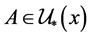 ,取
,取 ,则
,则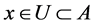 ,
,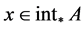 ,故
,故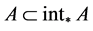 ,
,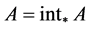 。
。
(2) 由闭包的定义 ,下证
,下证 。事实上,由于
。事实上,由于 为闭集,故
为闭集,故 为开集,故
为开集,故 ,
,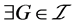 使
使 ,故
,故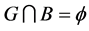 ,即
,即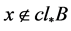 。所以,
。所以,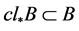 。从而
。从而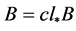 。
。
在§4中,我们将通过例4.1和例4.2说明上述命题的逆命题是不成立的。
命题2.2:设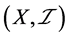 是一个ISTS,
是一个ISTS,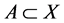 ,则
,则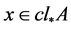 当且仅当对
当且仅当对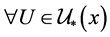 ,有
,有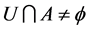 。
。
证明:必要性:设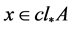 ,因为
,因为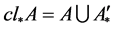 ,则
,则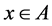 或者
或者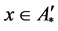 。若
。若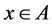 ,则对
,则对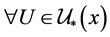 ,
, ;若
;若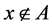 ,则
,则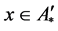 ,由聚点的定义,对
,由聚点的定义,对 ,
,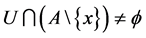 ,故
,故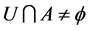 。
。
充分性:假设 ,则
,则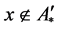 。故
。故 ,
, 。又因为
。又因为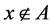 ,故
,故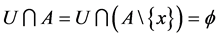 ,这与
,这与 ,有
,有 矛盾。因此,
矛盾。因此, 。
。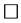
命题2.3:设 是一个ISTS,
是一个ISTS, 是
是 的任意子集,则
的任意子集,则 。
。
证明:由闭包的定义知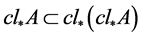 ,下证
,下证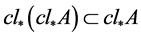 。
。
事实上,对 ,
, ,有
,有 。因
。因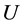 是点
是点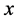 的邻域,故
的邻域,故 ,使
,使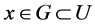 ,因为
,因为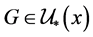 ,故
,故 ,取
,取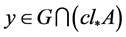 ,则
,则 ,故
,故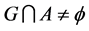 ,从而
,从而 。于是
。于是 ,故
,故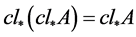 。
。
3. 关于分离性质的一些结果
由定义1.8和定义1.9,显然有:
定理3.1: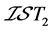 空间
空间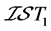
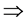 空间
空间
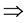 空间。
空间。
在§4中,例4.3与例4.4将说明上述定理的不可逆性。关于这三类分离性质,我们有如下等价刻画:
定理3.2:设 是一个ISTS,则
是一个ISTS,则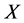 为
为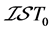 空间当且仅当对
空间当且仅当对 :
: ,
,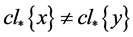 。
。
证明:充分性:(反证)。假设 不是
不是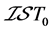 空间,则
空间,则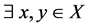 :
: ,使得
,使得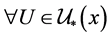 有
有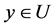 ,并且对
,并且对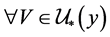 有
有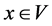 ,故
,故 且
且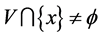 。命题2.2知,
。命题2.2知,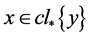 并且
并且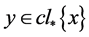 。再由命题2.3,有
。再由命题2.3,有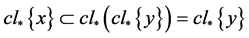 并且
并且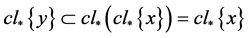 ,故
,故 。这与对
。这与对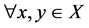 :
: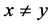 ,
,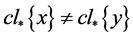 矛盾,故
矛盾,故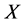 是
是 空间。
空间。
必要性:设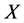 为
为 空间,
空间,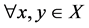 ,若
,若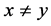 ,则
,则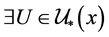 使得
使得 ,或者
,或者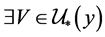 。
。
使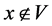 。不妨设
。不妨设 使得
使得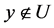 ,则
,则 使
使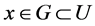 ,且
,且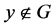 。因此,
。因此,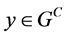 。故
。故 ,即
,即 。因此,
。因此, 。
。
定理3.3:设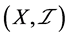 是一个ISTS,则
是一个ISTS,则 为
为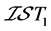 空间当且仅当对
空间当且仅当对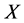 的每个单点集
的每个单点集 ,都有
,都有 。
。
证明:充分性: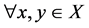 ,
,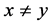 ,则
,则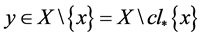 ,则
,则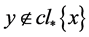 ,由引理2.2知,
,由引理2.2知,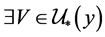 ,使得
,使得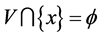 ,故
,故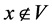 。同理,
。同理,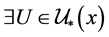 ,使得
,使得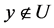 ,故
,故 为
为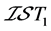 空间。
空间。
必要性:对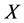 的每个单点集
的每个单点集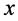 ,由闭包的定义知
,由闭包的定义知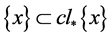 成立,下证
成立,下证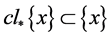 成立。事实上,对
成立。事实上,对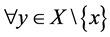 ,有
,有 ,由
,由 为
为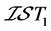 空间,则
空间,则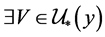 使得
使得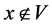 ,故
,故 ,从而,
,从而, ,即
,即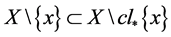 ,故
,故 。从而,
。从而, ,
, 。
。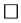
定理3.4:设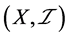 是一个S-ISTS,则
是一个S-ISTS,则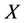 为
为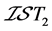 空间当且仅当
空间当且仅当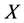 中的每个收敛网都有唯一极限。
中的每个收敛网都有唯一极限。
证明:必要性:(反证),假设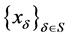 是
是 中的一个网,并且
中的一个网,并且 ,
, ,其中
,其中 。
。
由 ,对
,对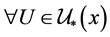 ,
, ,
,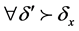 有
有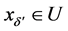 ;同理
;同理 。
。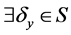 ,
,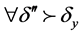
有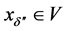 。取
。取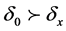 且
且 ,则当
,则当 时,有
时,有 。这与
。这与 是
是 空间矛盾。
空间矛盾。
充分性:(反证)。若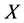 不是
不是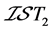 空间,则
空间,则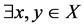 ,
,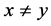 使得
使得 ,
,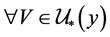 ,有
,有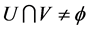 。取
。取 ,并且定义:
,并且定义:
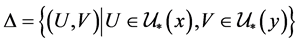
在 上定义半序关系“
上定义半序关系“ ”:
”: 当且仅当
当且仅当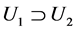 且
且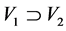 ,则
,则 是一个定向集。因此,
是一个定向集。因此, 为
为 中的网并且
中的网并且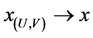 ,
,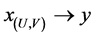 ,这与
,这与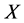 中的每个收敛网都有唯一极限矛盾。
中的每个收敛网都有唯一极限矛盾。
在§4中,将用例4.5~例4.8四个反例来说明: 、
、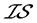 -正则与
-正则与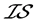 -正规三者是互相不蕴含的,而且关于
-正规三者是互相不蕴含的,而且关于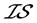 -正则与
-正则与 -正规,至今还没能类似于定理3.2~定理3.4的任何等价刻画。关这两种分离性质,我们仅得到如下两个类似于拓扑空间的定理:
-正规,至今还没能类似于定理3.2~定理3.4的任何等价刻画。关这两种分离性质,我们仅得到如下两个类似于拓扑空间的定理:
定理3.5:设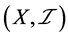 是S-ISTS,若
是S-ISTS,若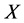 为
为 -正则空间,则
-正则空间,则 ,
, ,
,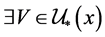 ,使得
,使得 。
。
证明:对 ,
, ,
, ,使得
,使得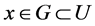 ,
,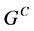 闭于
闭于 且
且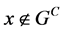 ,因为
,因为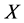 为
为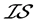 -正则空间,则
-正则空间,则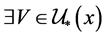 ,存在开集
,存在开集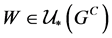 ,使得
,使得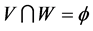 。因此,
。因此,
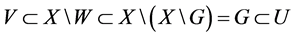
由于 是开集,故
是开集,故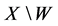 为闭集。因此,
为闭集。因此, 。
。
定理3.6:设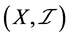 是一个S-ISTS,若
是一个S-ISTS,若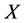 为
为 -正规空间,则对
-正规空间,则对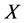 中的任意闭集
中的任意闭集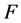 ,
, ,
, ,使得
,使得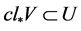 。
。
证明:设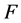 是
是 的任一闭集,
的任一闭集, ,
, ,使得
,使得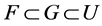 。则
。则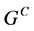 为
为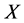 中的闭集并且
中的闭集并且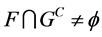 ,则存在
,则存在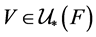 ,存在开集
,存在开集 ,使得
,使得 。故
。故 并且
并且 。故
。故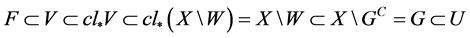 。
。
上述两个定理的逆命题是不成立的,关于这点在例4.9说明。
4 下半拓扑空间中的反例
首先用下面两例分别说明:命题2.1(1)与命题2.1(2)的逆命题是不真的。
例4.1:存在下半拓扑空间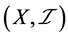 ,
,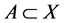 并且
并且 成立,但
成立,但 。
。
事实上,可取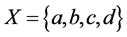 ,
,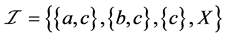 ,则
,则 是一个下半拓扑空间。又取
是一个下半拓扑空间。又取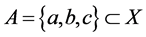 ,则
,则 。这是因为
。这是因为 ,
, 使得
使得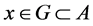 。故
。故 ,但
,但 。
。
例4.2:存在下半拓扑空间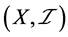 ,
, 且
且 成立,
成立,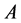 不是
不是 中的闭集。
中的闭集。
事实上,设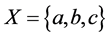 ,
,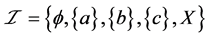 ,则
,则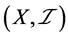 是一个下半拓扑空间。由定理2.2推得,
是一个下半拓扑空间。由定理2.2推得,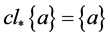 。但
。但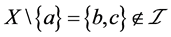 ,从而
,从而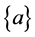 不是
不是 中的闭集。
中的闭集。
现在,用如下两例说明定理3.1的每个逆命题都是不成立的:
例4.3:存在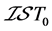 空间不是
空间不是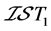 空间。事实上,取
空间。事实上,取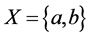 ,
,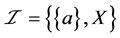 ,易知
,易知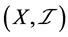 是一个下半拓扑空间,则
是一个下半拓扑空间,则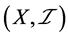 是
是 空间,但不是
空间,但不是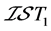 空间。
空间。
例4.4:存在 空间不是
空间不是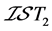 空间。设
空间。设 为实数集,
为实数集, {
{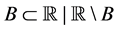 至多可数},易知
至多可数},易知 是一个下半拓扑空间,则
是一个下半拓扑空间,则 是
是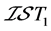 空间,但
空间,但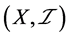 不是
不是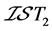 空间。
空间。
事实上, ,若
,若 ,则
,则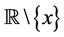 为
为 的一个不包含
的一个不包含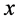 邻域,
邻域, 为
为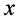 的一个不包含
的一个不包含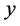 邻域。因此,
邻域。因此, 是
是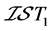 空间。若
空间。若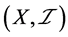 是
是 空间,则对
空间,则对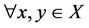 ,
,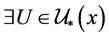 ,
, 使得
使得 。因为
。因为 ,
, ,故存在至多可数集
,故存在至多可数集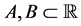 使得
使得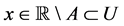 ,
,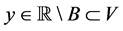 。故
。故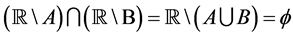 。因此,
。因此, 。这与
。这与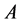 ,
,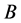 是不可数集矛盾。从而,
是不可数集矛盾。从而,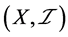 不是
不是 空间。
空间。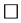
问题3: 与
与 -正则和
-正则和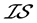 -正规之间是否存在蕴含关系呢?
-正规之间是否存在蕴含关系呢?
下面的两个例子分别说明: 与
与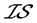 -正则以及
-正则以及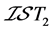 与
与 -正规之间均不存在蕴含关系。
-正规之间均不存在蕴含关系。
例4.5:存在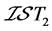 空间不是
空间不是 -正则的,也不是
-正则的,也不是 -正规的。设
-正规的。设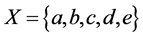 ,
, ,则
,则 是一个
是一个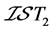 空间。但
空间。但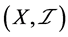 不是
不是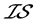 -正则空间,也不是
-正则空间,也不是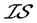 -正规空间。
-正规空间。
事实上,可取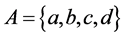 ,
,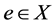 ,则
,则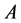 是
是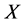 的闭集且
的闭集且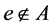 ,
,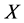 是唯一包含
是唯一包含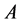 的开集。故
的开集。故 ,
,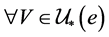 有
有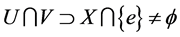 。因此,
。因此,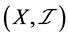 不是
不是 -正则空间。此外,取
-正则空间。此外,取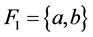 ,
,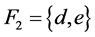 ,则
,则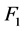 ,
, 是
是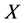 中闭集,并且
中闭集,并且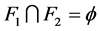 。因为
。因为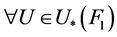 ,
, 都有
都有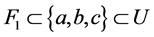 ,并且
,并且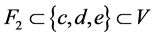 ,故
,故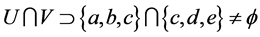 。因此,
。因此, 不是
不是 -正规空间。
-正规空间。
例4.6:存在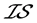 -正则空间、
-正则空间、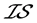 -正规空间不是
-正规空间不是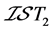 空间。
空间。
设 ,
,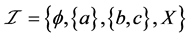 ,则
,则 为
为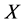 上的一个下半拓扑并且
上的一个下半拓扑并且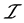 也是
也是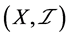 中闭集全体,所以
中闭集全体,所以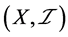 是
是 -正则空间,也是
-正则空间,也是 -正规空间。但
-正规空间。但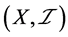 不是
不是 空间。从而,也不是
空间。从而,也不是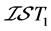 空间和
空间和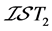 空间。事实上,对于
空间。事实上,对于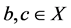 :
: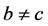 ,不存在
,不存在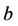 的邻域
的邻域 使得
使得 ,也不存在
,也不存在 的邻域
的邻域 ,使得
,使得 。故
。故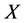 不是
不是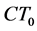 空间。
空间。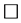
问题4: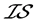 -正则空间和
-正则空间和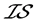 -正规空间是否有相互蕴含关系呢?
-正规空间是否有相互蕴含关系呢?
下面的两个例子说明:它们两者也没有蕴含关系。
例4.7:存在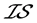 -正则空间不是
-正则空间不是 -正规空间。设
-正规空间。设 ,并令
,并令
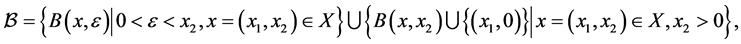
又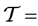 {
{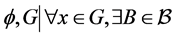 使得
使得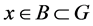 },则
},则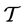 是以
是以 为基的拓扑,且
为基的拓扑,且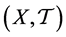 是正则空间,但不是正规空间[10] 。故
是正则空间,但不是正规空间[10] 。故 是
是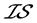 -正则空间,但不是
-正则空间,但不是 -正规空间。
-正规空间。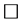
例4.8:存在 -正规空间不是
-正规空间不是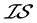 -正则空间。设
-正则空间。设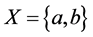 ,
,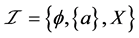 ,则
,则 是一个
是一个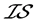 - 正规空间,但不是
- 正规空间,但不是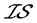 -正则空间。
-正则空间。
事实上,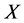 中的闭集全体为
中的闭集全体为 ,故
,故 没有不相交的非空闭集。因此,是一个
没有不相交的非空闭集。因此,是一个 -正规空间。此外,取
-正规空间。此外,取 闭于
闭于 ,
,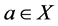 ,由于
,由于 是包含
是包含 的唯一开集,则
的唯一开集,则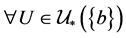 ,
, 有
有 。所以,
。所以, 不是
不是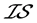 -正则空间。
-正则空间。
虽然,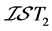 空间、
空间、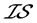 -正则空间与
-正则空间与 -正规空间之间不存在任何蕴含关系,但是根据定义1.8,下面结论成立是显然的:
-正规空间之间不存在任何蕴含关系,但是根据定义1.8,下面结论成立是显然的:
定理4.1:设 是一个S-ISTS,如果
是一个S-ISTS,如果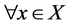 ,单点集
,单点集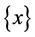 是下半闭集,则有
是下半闭集,则有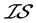 -正规空间
-正规空间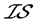
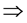 -正则空间
-正则空间
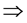 空间。
空间。
最后,我们用下面两个例子分别说明:定理3.5和定理3.6的逆命题都是不成立的。
例4.9:存在下半拓扑空间 ,对
,对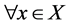 ,
,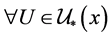 ,
,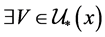 使
使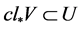 成立,但
成立,但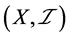 不是
不是 -正则空间;也存在下半拓扑空间
-正则空间;也存在下半拓扑空间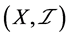 ,对
,对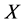 中的任意闭集
中的任意闭集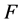 ,
,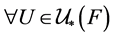 ,
, 使得
使得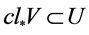 ,但
,但 不是
不是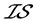 -正规的。
-正规的。
事实上,可取 ,
, ,由命题2.3推知,
,由命题2.3推知,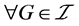 ,都有
,都有 。这是因为
。这是因为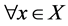 ,
, ,都有
,都有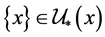 ,但
,但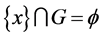 ,故
,故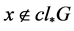 。因此,对
。因此,对 ,
,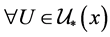 ,
,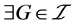 ,使得
,使得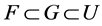 ,因为
,因为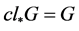 ,所以
,所以 且
且 。对于
。对于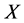 中的任意闭集
中的任意闭集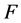 ,
, ,
,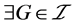 ,使得
,使得 。因为
。因为 ,所以
,所以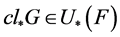 且
且 。
。
但由例4.5知,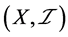 既不是
既不是 -正则空间,也不是
-正则空间,也不是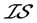 -正规空间。
-正规空间。
5. 小结
本文首先相对于广义拓扑(上半拓扑),对偶地引入下半拓扑的概念。然后类比拓扑空间的点集理论与分离性质,引入下半拓扑空间中相应的基本点集与分离性质。进而使拓扑空间的分离性质: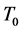 、
、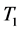 、
、 以及正则性和正规性分别被推广为下半拓扑空间中的
以及正则性和正规性分别被推广为下半拓扑空间中的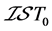 、
、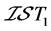 、
、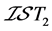 、
、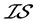 -正规和
-正规和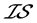 -正则空间,并且先后给出了上述5种分离性质之间的蕴含关系以及
-正则空间,并且先后给出了上述5种分离性质之间的蕴含关系以及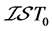 、
、 和
和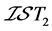 三种分离性质的等价刻画。此外,还分别给出了
三种分离性质的等价刻画。此外,还分别给出了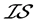 -正规和
-正规和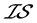 -正则分离性质的必要条件,并且分别通过反例指出:所得到的
-正则分离性质的必要条件,并且分别通过反例指出:所得到的 -正规和
-正规和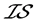 -正则的必要条件的逆命题不真。
-正则的必要条件的逆命题不真。
致谢
感谢电子科技大学科研实训创新项目基金的经费资助。
文章引用
胡西超,朱培勇, (2015) 一类新型半拓扑空间及其分离性质
A New Semi-Topological Space and Its Separation Property. 理论数学,04,129-135. doi: 10.12677/PM.2015.54020
参考文献 (References)
- 1. Csaszar, A. (2005) Generalized open sets in generalized topologies. Acta Mathematica Hungarica, 106, 53-66. http://dx.doi.org/10.1007/s10474-005-0005-5
- 2. Min, W.K. (2009) Weak continuity on generalized topological spaces. Acta Mathematica Hungarica, 124, 73-81. http://dx.doi.org/10.1007/s10474-008-8152-0
- 3. Min, W.K. (2009) Almost continuity on generalized topological spaces. Acta Mathematica Hungarica, 125, 121-125. http://dx.doi.org/10.1007/s10474-009-8230-y
- 4. Csaszar, A. (2008) On generalized neighbourhood systems. Acta Mathematica Hungarica, 121, 395-400. http://dx.doi.org/10.1007/s10474-008-7224-5
- 5. Sarma, R.D. (2010) On convergence in generalized topology. In-ternational Journal of Pure and Applied Mathematics, 60, 51-56.
- 6. Sarm, R.D. (2012) On extremely disconnected generalized topologies. Acta Mathematica Hungarica, 134, 583-588. http://dx.doi.org/10.1007/s10474-011-0153-8
- 7. Wu, X. and Zhu, P. (2013) A note on β-connectedness. Acta Ma-thematica Hungarica, 139, 252-254. http://dx.doi.org/10.1007/s10474-012-0276-6
- 8. Csaszar, A. (2002) Generalized topology, generalized continuity. Acta Mathematica Hungarica, 96, 351-357. http://dx.doi.org/10.1023/A:1019713018007
- 9. 朱培勇, 雷银彬 (2009) 拓扑学导论. 科学出版社, 北京.
- 10. 熊金城 (2011) 点集拓扑讲义. 第四版, 高等教育出版社, 北京.