Pure Mathematics
Vol.4 No.05(2014), Article ID:14050,4 pages
DOI:10.12677/PM.2014.45025
The Influence of π Supplemented Subgroups on Finite Groups
College of Applied Mathematics, Chengdu University of Information Technology, Chengdu
Email: baojunli@cuit.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 8th, 2014; revised: Aug. 6th, 2014; accepted: Aug. 15th, 2014
ABSTRACT
Let
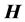 be a subgroup
be a subgroup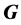 . If every chief
factor
. If every chief
factor
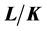 of
of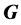 ,
,
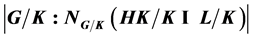 is a
is a
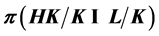 -number, then
-number, then
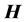 is called satisfying πproperty in
is called satisfying πproperty in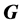 . If there exists
a subgroup
. If there exists
a subgroup
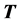 of
of
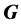 such that
such that
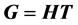 and
and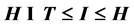 , where
, where
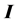 satisfies πproperty in
satisfies πproperty in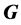 , then
, then
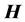 is called πsupplemented in
is called πsupplemented in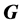 . By the property
of πsupplemented, some new criterion of p-nilpotency of finite groups is obtained.
. By the property
of πsupplemented, some new criterion of p-nilpotency of finite groups is obtained.
Keywords:Finite Groups, p-Nilpotent, πSupplemented

π-可补充子群对有限群结构的影响
李保军,刘阿明
成都信息工程学院应用数学学院,成都
Email: baojunli@cuit.edu.cn
收稿日期:2014年7月8日;修回日期:2014年8月6日;录用日期:2014年8月15日

摘 要
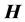 是群
是群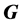 的子群,如果对群
的子群,如果对群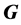 的任意主因子
的任意主因子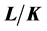 ,
,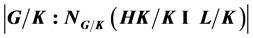 是
是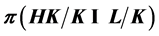 -数,则称
-数,则称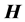 在
在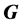 中满足π性质;如果存在
中满足π性质;如果存在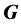 的子群
的子群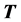 使得
使得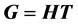 ,并且
,并且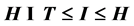 ,其中
,其中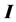 在
在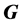 中满足π性质,则称
中满足π性质,则称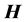 在
在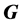 中是π可补充的。利用子群的π可补充性,得到了有限群p-幂零性的一个新的判定方法。
中是π可补充的。利用子群的π可补充性,得到了有限群p-幂零性的一个新的判定方法。
关键词
有限群,p-幂零,π-可补

1. 引言
本文所讨论的群皆为有限群。文中所用的符号和概念都是标准的,对未交代的符号和概念,读者可参阅文献[1] 和[2] 。本文中,我们用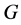 表示一个群;
表示一个群;![]() 表示素数的一个集合,
表示素数的一个集合,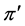 为
为![]() 在所有素数集合中的补集(当
在所有素数集合中的补集(当![]() 仅包含一个素数
仅包含一个素数![]() 时,我们记作
时,我们记作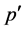 );
);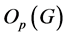 为
为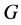 的最大正规
的最大正规![]() -子群,相应地,
-子群,相应地,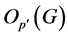 为
为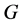 的最大正规
的最大正规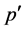 -子群。
-子群。
众所周知,早在1939年,O. Ore就在Duke Math上发表文章[3] ,给出子群置换的概念,如果 那么群
那么群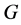 的子群
的子群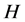 和
和![]() 称为可置换的;如果
称为可置换的;如果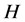 和
和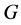 的任意子群可置换,那么
的任意子群可置换,那么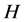 称为
称为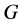 的拟正规子群或置换子群[4]
。作为这一工作的推广,W. E. Deskins和O. Kegel分别在文章[5] 和[6] 引入了
的拟正规子群或置换子群[4]
。作为这一工作的推广,W. E. Deskins和O. Kegel分别在文章[5] 和[6] 引入了![]() -拟正规子群(即和所有Sylow子群可置换的子群),并得到了一些和子群置换类似的性质和结论。此后,子群各类广义置换性质被不断提出和研究,其中包括王燕鸣在文章[7]
提出的
-拟正规子群(即和所有Sylow子群可置换的子群),并得到了一些和子群置换类似的性质和结论。此后,子群各类广义置换性质被不断提出和研究,其中包括王燕鸣在文章[7]
提出的![]() -正规子群;M. Asaad在文章[8] 中提出的
-正规子群;M. Asaad在文章[8] 中提出的![]() - 置换子群;郭文彬等[9] 提出的X-置换子群;苏向盈[10]
和T. Foguel [11] 研究的半正规子群,胡滨等[12] 讨论的
- 置换子群;郭文彬等[9] 提出的X-置换子群;苏向盈[10]
和T. Foguel [11] 研究的半正规子群,胡滨等[12] 讨论的![]() -半置换子群;李保军、张志让[13] 研究的
-半置换子群;李保军、张志让[13] 研究的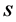 -条件置换子群以及A.Ahnmad等[14]
中引入的
-条件置换子群以及A.Ahnmad等[14]
中引入的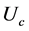 -正规子群等。近年来,Skiba [15] 利用特定阶的准素子群的弱s-置换性刻画群结构是子群广义置换研究方面的一个出色工作。
-正规子群等。近年来,Skiba [15] 利用特定阶的准素子群的弱s-置换性刻画群结构是子群广义置换研究方面的一个出色工作。
对子群置换性质的研究,一个自然的问题是,对于各类广义子群置换子群,它们是否有共同的性质?基于这一问题的思考,李保军[16] 引入了子群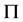 -性质和
-性质和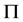 -可补充性质的概念:
-可补充性质的概念:
定义1.1 [16] :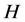 是群
是群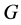 的子群,如果对群
的子群,如果对群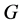 的任意主因子
的任意主因子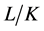 ,
,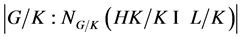 是
是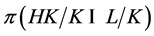 数,则称
数,则称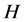 在
在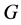 中满足
中满足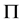 -性质;如果存在
-性质;如果存在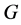 的子群
的子群![]() 使得
使得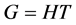 ,并且
,并且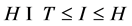 ,其中
,其中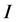 在
在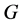 中满足
中满足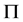 -性质,则称
-性质,则称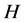 在
在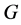 中是
中是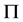 -可补充的.
-可补充的.
文[16] 的工作表明,子群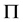 -性质为众多已有广义置换性质的一个本质特征。利用子群的
-性质为众多已有广义置换性质的一个本质特征。利用子群的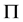 -性质和
-性质和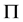 - 可补充性质,我们已得到了群结构的一些好的描述(参见[16]
[17] ),本文我们将进一步研究
- 可补充性质,我们已得到了群结构的一些好的描述(参见[16]
[17] ),本文我们将进一步研究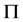 -可补充子群与群的幂零性的联系。
-可补充子群与群的幂零性的联系。
2. 一些基本性质和引理
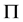 -可补充子群的概念是建立在子群
-可补充子群的概念是建立在子群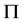 -性质上的,而我们知道
-性质上的,而我们知道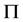 -性质是子群的一类重要性质,众多被广泛研究的广义置换子群都具有
-性质是子群的一类重要性质,众多被广泛研究的广义置换子群都具有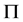 -性质。
-性质。
命题2.1:([15] ,命题2.2)设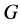 是群,
是群,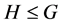 ,如果满足下列条件之一,那么
,如果满足下列条件之一,那么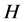 在
在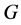 中就具有
中就具有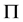 -性质:
-性质:
(1)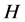 在
在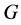 中是正规的;
中是正规的;
(2)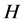 在
在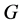 中是拟正规的;
中是拟正规的;
(3)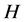 在
在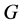 中是
中是![]() -拟正规的;
-拟正规的;
(4)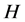 在
在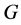 中是与
中是与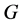 的所有Sylow子群
的所有Sylow子群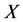 -可置换的,其中
-可置换的,其中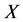 是
是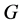 的一个可解正规子群。
的一个可解正规子群。
回忆,设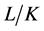 是群
是群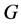 的一个主因子,
的一个主因子,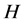 是
是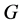 的一个子群,若
的一个子群,若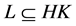 ,则称
,则称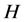 覆盖
覆盖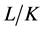 ;若
;若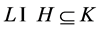 ,则称
,则称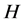 避开
避开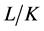 ;如果
;如果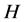 覆盖或者避开群
覆盖或者避开群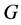 的任意一个主因子,则称
的任意一个主因子,则称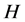 是群
是群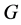 的一个
的一个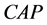 -子群。群
-子群。群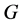 的一个正规子群
的一个正规子群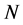 称为超可解超中心的,如果
称为超可解超中心的,如果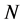 的所有
的所有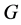 -主因子循环。群
-主因子循环。群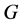 的所有这样的正规子群
的所有这样的正规子群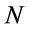 的积称为
的积称为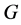 的超可解超中心,记作
的超可解超中心,记作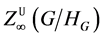 。
。
命题2.2:([15] ,命题2.3)设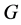 是群,
是群,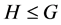 ,当满足下列条件之一时,则
,当满足下列条件之一时,则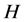 在
在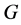 中具有
中具有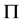 -性质:
-性质:
(1)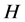 是
是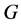 的一个
的一个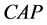 -子群
-子群
(2)
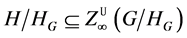
我们需要以下引理来证明我们文章的主要结果。
引理2.1:([17] ,引理2.1)设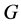 是群,
是群,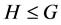 ,
,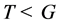 ,则有下面结论:
,则有下面结论:
(1) 如果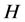 在
在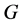 中具有
中具有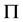 -性质,那么
-性质,那么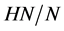 在
在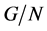 具有
具有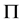 -性质;
-性质;
(2) 如果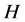 在
在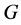 中具有
中具有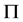 -性质,那么
-性质,那么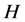 在
在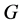 中是
中是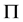 -可补充的;
-可补充的;
(3)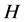 在
在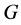 中是
中是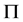 -可补充的,如果
-可补充的,如果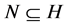 或者
或者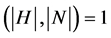 ,那么
,那么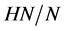 在
在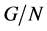 是
是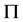 -可补充的;
-可补充的;
(4)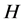 在
在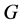 中是
中是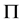 -可补充的,则
-可补充的,则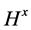 在
在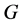 中是
中是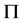 -可补充的,对任意
-可补充的,对任意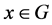 。
。
引理2.2:([17] ,引理2.3)设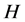 为
为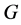 的
的![]() -子群,
-子群,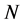 为
为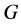 的极小正规子群。又设
的极小正规子群。又设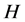 在
在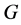 中是
中是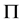 -可补充的。如果
-可补充的。如果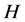 正规与
正规与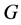 的某个Slow
的某个Slow![]() -子群
-子群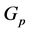 ,则
,则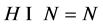 或1。
或1。
引理2.3:设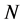 为
为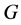 的正规
的正规![]() -子群且
-子群且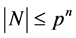 。如果
。如果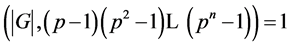 ,则
,则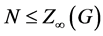 。
。
证明:设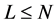 为
为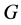 的一个极小正规子群。则
的一个极小正规子群。则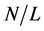 为
为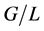 的正规
的正规![]() -子群且
-子群且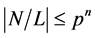 。显然
。显然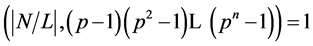 仍成立。因此,由归纳,
仍成立。因此,由归纳,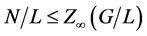 。于是我们只需证明
。于是我们只需证明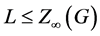 。设
。设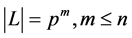 。由
。由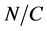 定理(参见[2]
,第I章,定理5.7),
定理(参见[2]
,第I章,定理5.7),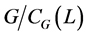 同构与
同构与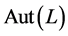 的一个子群。但由
的一个子群。但由
于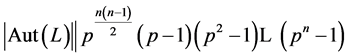 且
且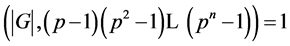 ,因此
,因此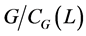 为
为![]() -群。由
-群。由
[1, 1.7.11]知,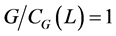 ,即
,即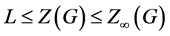 。引理成立。
。引理成立。
引理2.4:([17] ,定理1.3)设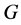 为一个群
为一个群![]() 为素数且
为素数且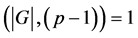 。又设
。又设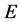 为
为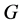 的一个正规子群满足
的一个正规子群满足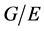 为
为![]() -幂零群,
-幂零群,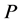 为
为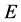 的一个Sylow
的一个Sylow![]() -子群。如果
-子群。如果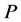 的所有
的所有![]() 阶和4阶(当
阶和4阶(当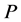 为非交换2-群)子群在
为非交换2-群)子群在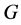 中是
中是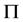 -可补充的,则
-可补充的,则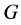 为
为![]() -幂零群。
-幂零群。
3. π可补充子群与群的p-幂零性
定理3.1:设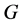 为一个群
为一个群![]() 为奇素数且
为奇素数且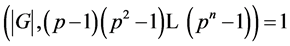 。又设
。又设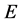 为
为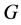 的一个正规子群满足
的一个正规子群满足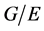 为
为![]() -幂零群,
-幂零群,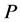 为
为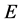 的一个Sylow
的一个Sylow![]() -子群。如果
-子群。如果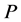 的所有
的所有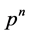 阶子群在
阶子群在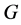 中是
中是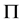 -可补充的,则
-可补充的,则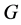 为
为![]() -幂零群。
-幂零群。
证明:设结论不成立并设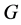 为极小阶反例,即所有满足定理条件且阶小于
为极小阶反例,即所有满足定理条件且阶小于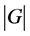 的群为
的群为![]() -幂零群。我们通过以下步骤完成证明。
-幂零群。我们通过以下步骤完成证明。
(1)
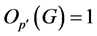
显然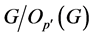 有正规子群
有正规子群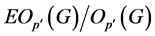 满足
满足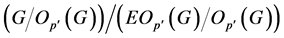 ,且
,且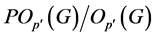 为
为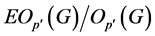 的一个Sylow
的一个Sylow![]() -子群。由引理2.1,
-子群。由引理2.1,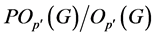 的所有
的所有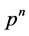 阶子群在
阶子群在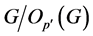 中是
中是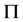 -可补充的。另一方面,
-可补充的。另一方面,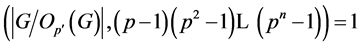 显然成立。因此,由
显然成立。因此,由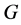 的选择,
的选择,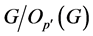 为为
为为![]() -幂零群,而由此又立即可得出
-幂零群,而由此又立即可得出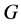 为
为![]() 幂零群,矛盾于
幂零群,矛盾于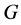 的选择。(1)成立。
的选择。(1)成立。
(2)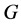 可解且
可解且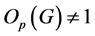 .
.
因为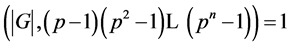 且
且![]() 为奇素数,知
为奇素数,知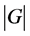 与2互素,即
与2互素,即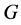 为奇阶群。由Feit-Thompson奇阶群定理得
为奇阶群。由Feit-Thompson奇阶群定理得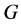 可解。进而由(1)得
可解。进而由(1)得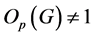 (参见[2] ,第V章,定理1.5(4))。
(参见[2] ,第V章,定理1.5(4))。
(3) 设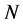 为
为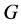 的一个极小正规子群且
的一个极小正规子群且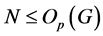 。则
。则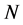 为
为![]() 阶循环群且
阶循环群且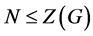 。
。
因为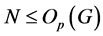 ,所以
,所以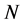 为交换
为交换![]() -群。若
-群。若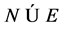 ,则
,则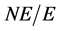 为
为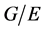 的主因子。但
的主因子。但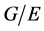 为
为![]() -幂零群,因此
-幂零群,因此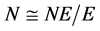 为
为![]() 阶循环群。设
阶循环群。设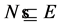 。如果
。如果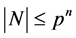 ,则由引理2.3知
,则由引理2.3知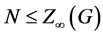 。由
。由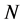 为
为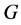 的一个极小正规子群得
的一个极小正规子群得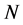 为
为![]() 阶循环群且
阶循环群且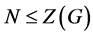 。设
。设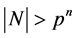 ,则
,则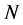 有真子群
有真子群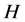 使得
使得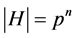 ,并且由
,并且由![]() 群性质(参见[2]
,第IV章,定理5.4)可设
群性质(参见[2]
,第IV章,定理5.4)可设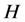 为
为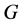 的Sylow
的Sylow![]() -子群
-子群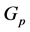 的正规子群。由定理条件,
的正规子群。由定理条件,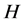 在
在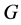 中是
中是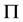 -可补充的。因此存在
-可补充的。因此存在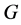 的子群
的子群![]() ,使得
,使得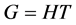 且
且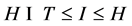 ,其中
,其中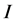 在
在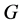 中有
中有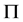 -性质。由于
-性质。由于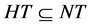 ,
,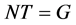 。显然
。显然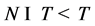 。另一方面,由于
。另一方面,由于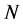 为交换群,
为交换群,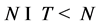 。因此
。因此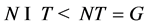 。如果
。如果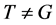 ,则
,则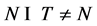 ,从而
,从而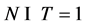 。于是
。于是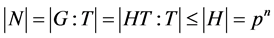 ,矛盾。因此
,矛盾。因此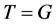 且进而有
且进而有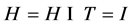 在
在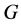 中有
中有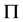 -性质。由引理2.2,得
-性质。由引理2.2,得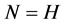 ,矛盾。(3)成立。
,矛盾。(3)成立。
(4) 最后的矛盾
由![]() 为奇数且
为奇数且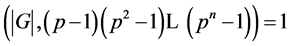 ,知
,知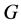 为奇数阶群。由Feit-Thompson奇阶群定理知
为奇数阶群。由Feit-Thompson奇阶群定理知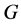 为可解群。由(1)及[2] ,第V章,定理1.6,
为可解群。由(1)及[2] ,第V章,定理1.6,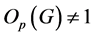 。令
。令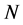 为
为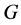 的一个极小正规子群且
的一个极小正规子群且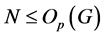 。由(3),
。由(3),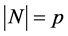 。因此由引理2.1,
。因此由引理2.1,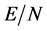 的Sylow
的Sylow![]() -子群
-子群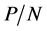 的所有
的所有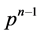 阶子群在
阶子群在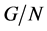 中
中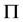 -可补充的。由于当
-可补充的。由于当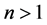 时,
时,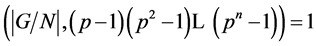 显然成立。因此由归纳,此时有
显然成立。因此由归纳,此时有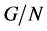 为
为![]() -幂零群。又由(3),
-幂零群。又由(3),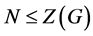 ,所以
,所以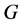 为
为![]() -幂零。若
-幂零。若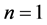 ,则由引理2.4可得
,则由引理2.4可得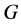 为
为![]() -幂零,与
-幂零,与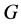 的选择(非
的选择(非![]() -幂零)矛盾。这一是最后一个矛盾,定理证明完成。
-幂零)矛盾。这一是最后一个矛盾,定理证明完成。
由命题2.1;2.2和引理2.1以及定理3.1,我们可以得到以下推论:
推论3.1:设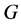 为一个群
为一个群![]() 为奇素数且
为奇素数且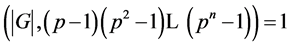 。又设
。又设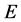 为
为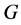 的一个正规子群满足
的一个正规子群满足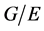 为
为![]() -幂零群,
-幂零群,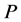 为
为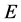 的一个Sylow
的一个Sylow![]() -子群。如果
-子群。如果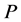 的所有
的所有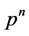 满足以下条件之一,则
满足以下条件之一,则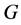 为
为![]() -幂零群:
-幂零群:
(1) 在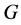 中是正规;
中是正规;
(2) 在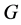 中拟正规;
中拟正规;
(3) 在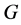 中是
中是![]() -拟正规;
-拟正规;
(4) 在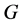 中是与
中是与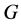 的所有Sylow子群
的所有Sylow子群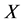 -可置换的,其中
-可置换的,其中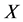 是
是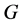 的一个可解正规子群;
的一个可解正规子群;
(5) 是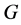 的一个
的一个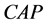 -子群;
-子群;
(6) 含于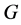 的超可解超中心中。
的超可解超中心中。
基金项目
国家自然科学基金资助项目(批准号11071229)。
参考文献 (References)
- [1] Guo, W. (2000) The theory of classes of groups. Science Press/Kluwer, Beijing/New York.
- [2] 徐明耀 (1999) 有限群导引. 科学出版社, 北京.
- [3] Ore, O. (1939) Contributions in the theory of groups of finite order. Duke Mathematical Journal, 5, 431-460.
- [4] Doerk, K. and Hawkes, T. (1992) Finite soluble groups. Walter de Gruyter, Berlin/New York.
- [5] Kegel, O. (1962) Sylow-Gruppen und Subnormalteiler endlicher Gruppen. Mathematische Zeitschrift, 78, 205-221.
- [6] Deskins, W. (1963) On quasinormal subgroups of finite groups. Mathematische Zeitschrift, 82, 125-132.
- [7] Wang, Y. (1996) c-Normality of groups and its properties. Journal of Algebra, 180, 954-965.
- [8] Asaad, M. and Heliel, A.A. (2003) On S-permutable subgroups of finite groups. Archiv der Mathematik, 80, 113-118.
- [9] Guo, W., Shum, K., Skiba, A., Guo, W., Skiba, A. and Shum, K. (2007) X-quasinormal subgroups. Siberian Mathematical Journal, 48, 593-605.
- [10] Su, X. (1988) Seminormal subgroups of finite groups. Journal of Mathematics (Chinese), 8, 7-9.
- [11] Foguel, T. (1994) On seminormal subgroups. Journal of Algebra, 165, 633-635.
- [12] Hu, B. and Guo, W. (2007) c-Semipermutable subgroups of finite groups. Siberian Mathematical Journal, 48, 180- 188.
- [13] Li, B.J. and Zhang, Z.R. (2009) The influence of s-conditionally permutable subgroups on finite groups. Science in China Series A: Mathematics, 52, 301-310.
- [14] Ahnmad, A. (2007) On Uc-normal subgroups of finite groups. Algebra Colloquium, 14, 25-36.
- [15] Skiba, A. (2007) On weakly s-permutable subgroups of finite groups. Journal of Algebra, 315, 192-209
- [16] Li, B. (2011) On Π-property and Π-normality of subgroups of finite groups. Journal of Algebra, 334, 321-337.
- [17] Li, B. (2011) Finite groups with Π-supplemented minimal Subgroups. Communications in Algebra, 41, 2060-2070.