Dynamical Systems and Control
Vol.05 No.01(2016), Article ID:16802,10
pages
10.12677/DSC.2016.51004
Stability Control and Circuit Implementation of a Novel 3D Chaotic System with Variable Coefficient
Hong Niu
College of Electronic Information and Automation, Tianjin University of Science & Technology, Tianjin

Received: Dec. 29th, 2015; accepted: Jan. 18th, 2016; published: Jan. 22nd, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, an analog circuit implementation of the three-dimensional autonomous chaotic system with variable coefficient is presented based on the modified module-based approach to chaotic circuit design. The chaotic phase portraits of the circuit are given to illustrate the good qualitative agreement between the numerical simulation and the experimental realization. Then, a linear feedback controller is designed via the Lyapunov stability theory so that the system is no longer chaotic or periodic but globally asymptotically converges to the equilibrium point at the origin. The designed controller is robust to the coefficient change of the nonlinear item. Moreover, after adding the controller circuit to the whole circuit implementation, the rapid change from chaos to convergence can be observed on the oscilloscope.
Keywords:3D Chaotic System with Variable Coefficient, Chaotic Circuit, Chaos Control

具有可变系数的三维混沌系统的稳定性控制与电路实现
牛弘
天津科技大学电子信息与自动化学院,天津

收稿日期:2015年12月29日;录用日期:2016年1月18日;发布日期:2016年1月22日

摘 要
本文基于改进型混沌电路模块化设计的方法,设计并搭建了具有可变系数的三维自治混沌系统的模拟电路实现,观察了实际电路产生的混沌运动曲线。而后,通过对该系统进行稳定性控制,使其不再产生混沌(或周期)运动而是全局渐近稳定于平衡点原点,且所设计的控制器对于该系统非线性部分系数的变化具有一定的鲁棒性。在此基础上,通过在实际电路中设计并加入相应的控制器电路,实现了实际电路由混沌运动状态迅速被稳定于平衡点原点的过程。
关键词 :具有可变系数的三维混沌系统,混沌电路,混沌控制

1. 引言
混沌运动由美国气象学家Lorenz于1963年首先发现[1] 。由于混沌具有丰富而复杂的非线性动力学行为,其不仅在理论上具有重大的研究价值,而且在实际上也具有广阔的应用前景。混沌模拟电路的设计与实现就是实际应用中的一个重要分支。由于模拟电路能产生真正的混沌运动,因此,用模拟电路验证混沌运动的存在是最具说服力的。许多科学工作者均就其提出的混沌系统给出了相应的模拟电路实现及运行结果 [2] - [7] ,以验证所设计混沌系统的实物可实现性。本文作者于文献 [8] 中提出了一个新三维混沌系统,为便于分析说明,本文中称该系统为N系统。N系统可通过调节其非线性部分中包含的可变系数实现不同系数组合下系统的混沌产生或混沌抑制。本文拟采用改进型混沌电路模块化设计的方法 [9] [10] ,设计N系统的模拟电路实现,验证N系统中混沌运动的存在性。
对于混沌控制,1990年,Ott、Grebogi和Yorke提出控制混沌的思想,并基于混沌轨道是由无穷多不稳定周期轨道构成的基本性质,提出了OGY方法 [11] [12] 。近年来,随着对混沌运动研究的不断深入,涌现出大量有效的混沌控制方法 [13] [14] ,这一研究方向一直是非线性科学领域的研究热点。针对N系统不易找到全局吸引域以及按照系统全局吸引域或混沌域范围设计控制器会增大控制器保守性的问题,本文拟采用先对被控N系统进行线性化,再证明被控N系统的全局渐近稳定性的改进型Lyapunov方法设计线性控制器,以实现N系统在可变系数范围内均不再产生混沌(或周期)运动,而是渐近稳定于平衡点原点。在此基础上,在实际电路中搭建相应的控制器电路,观察实际电路的控制效果。
2. N系统的电路实现
2.1. N系统
N系统的模型如下所示[8]
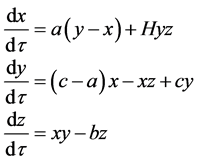 (1)
(1)
其中,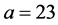 ,
,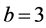 ,
,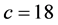 。
。 为可变系数。系统(1)随H变化的Lyapunov指数谱如图1中所示。当
为可变系数。系统(1)随H变化的Lyapunov指数谱如图1中所示。当 时,系统(1)处于周期运动状态;当
时,系统(1)处于周期运动状态;当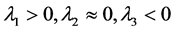 时,系统(1)处于混沌运动状态。
时,系统(1)处于混沌运动状态。
2.2. N系统的改进型模块化电路设计
2.2.1. 改进型混沌电路模块化设计
改进型混沌电路模块化设计不需要进行微分方程(状态方程)到积分方程的转换,而是通过直接比较混沌系统的状态方程与电路实现的状态方程的对应项系数来确定各元件的参数值 [10] ,该方法主要包括变量比例压缩变换、时间尺度变换、标准形式变换、电路模型设计、元件参数确定五个步骤。
2.2.2. N系统的模拟电路实现
本文所采用的运算放大器的型号均为TL082CP,乘法器的型号均为AD734AN,电源供电电压均为±15 V。由于运算放大器的饱和电压值为13.5 V,而通过数值仿真发现,系统(1)状态变量x的动态范围超出了±13.5 V,故需首先对x进行变量比例压缩变换。令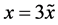 ,为简化标记,仍将
,为简化标记,仍将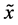 记为x。同时,为便于电路实现,对系统(1)进行时间尺度变换并改写为标准形式。令
记为x。同时,为便于电路实现,对系统(1)进行时间尺度变换并改写为标准形式。令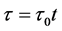 ,其中
,其中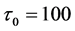 ,则
,则
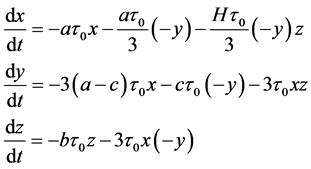 (2)
(2)
由式(2)设计相应的改进型模块电路并将输入、输出项对应连接,可得系统(2)的电路实现 [15] ,如图2中所示。
由图2,可得该电路实现的状态方程为
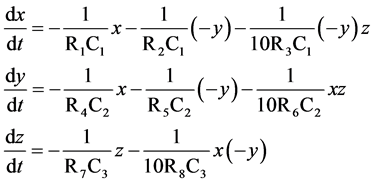 (3)
(3)
令式(3)与式(2)中对应项系数相等,已知电容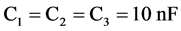 ,可得各电阻的阻值分别为
,可得各电阻的阻值分别为
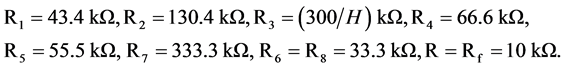
2.2.3. 电路运行结果
现以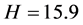 时的系统(2)为例,通过对比数值仿真曲线与实际电路运行曲线,说明如图2中所示的电路实现的正确性,并验证系统(1)中混沌运动的存在性。
时的系统(2)为例,通过对比数值仿真曲线与实际电路运行曲线,说明如图2中所示的电路实现的正确性,并验证系统(1)中混沌运动的存在性。
令系统(2)的初值为 ,此时系统的Lyapunov指数分别为
,此时系统的Lyapunov指数分别为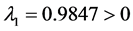 ,
,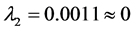 ,
, ,说明系统是混沌的,其相轨迹曲线如图3(a1)~(a3)中所示。
,说明系统是混沌的,其相轨迹曲线如图3(a1)~(a3)中所示。
由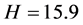 ,可得
,可得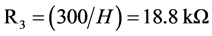 ,此时实际电路的运行曲线如图3(b1)~(b3)中所示。图中示波器显示刻度均为2 V/Div。
,此时实际电路的运行曲线如图3(b1)~(b3)中所示。图中示波器显示刻度均为2 V/Div。
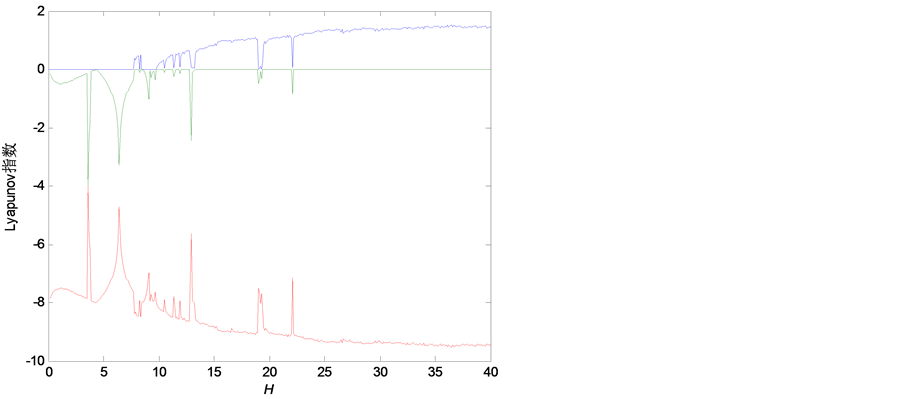
Figure 1. Lyapunov exponent spectrum of N system versus increasing H
图1. N系统随H变化的Lyapunov指数谱
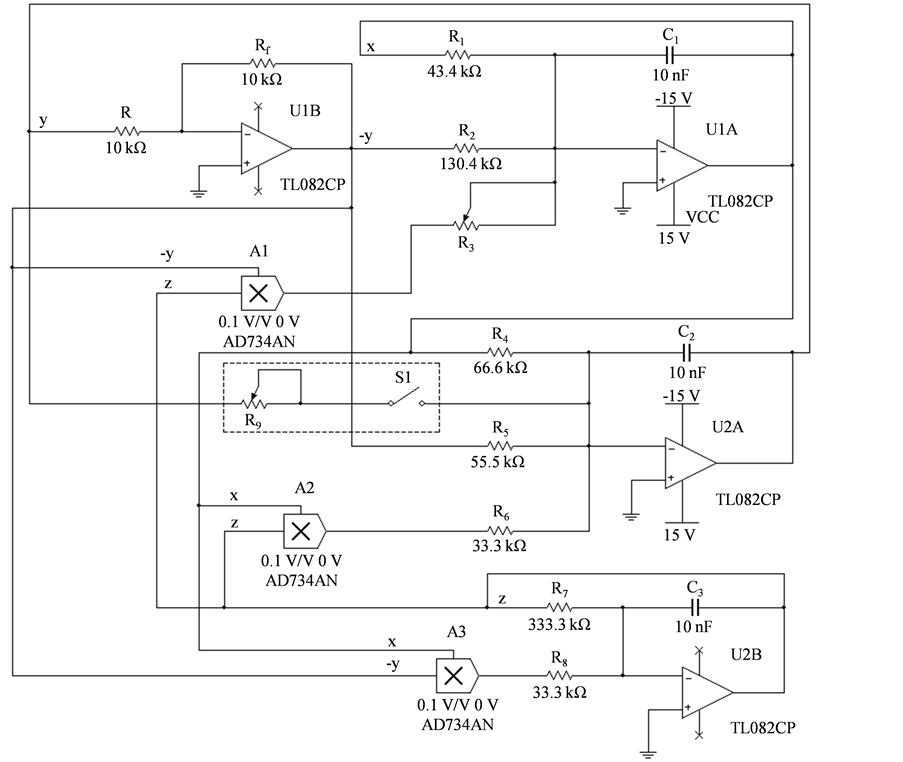
Figure 2. Circuit implementation of the system (2)
图2. 系统(2)的电路实现

Figure 3. Comparison of the phase portraits: simulation-experimental: (a1)-(b1) x-y; (a2)-(b2) x-z; (a3)-(b3) y-z
图3. 系统(2)理论仿真曲线与实际运行曲线的比较:(a1)~(b1) x-y;(a2)~(b2) x-z;(a3)~(b3) y-z
对比图3中(a1)~(a3)与(b1)~(b3)可以看出,两者一一对应且基本吻合,说明实际电路的相关参数是正确的,系统(1)确实可以产生混沌运动。该电路可用于对N系统(1)的稳定性控制的进一步研究。
3. N系统的稳定性控制
本文中的稳定性控制是指将H作为变化范围已知的不确定参数,通过加入控制器,使N系统(1)在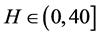 内均可全局渐近稳定于平衡点原点,而不再产生周期运动或混沌运动。令
内均可全局渐近稳定于平衡点原点,而不再产生周期运动或混沌运动。令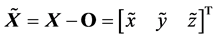 ,其中
,其中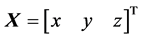 为系统(1)的状态变量,
为系统(1)的状态变量,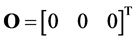 为原点,则被控系统可表示为 [15]
为原点,则被控系统可表示为 [15]
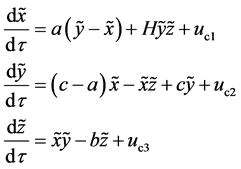 (4)
(4)
其中,
 (5)
(5)
为待设计的线性反馈控制器。
3.1. 被控系统的线性化
将式(5)代入式(4)中并对被控系统(4)在原点处进行线性化,得其线性化方程为
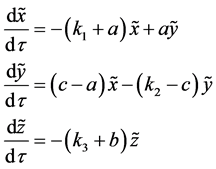 (6)
(6)
式(6)中不包含可变系数H,故可求出明确的控制参数范围。
取正定函数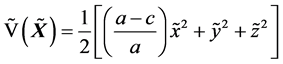 作为系统(6)的Lyapunov函数,其导数为
作为系统(6)的Lyapunov函数,其导数为
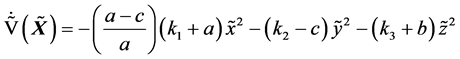
要使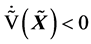 ,则
,则

此时系统(6)在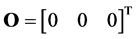 处是渐近稳定的。控制器
处是渐近稳定的。控制器 可简化为
可简化为
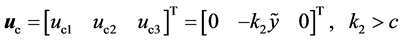 (7)
(7)
3.2. 被控系统的全局渐近稳定性
取径向无界的正定函数

作为系统(4)的Lyapunov函数,其导数为 [15]
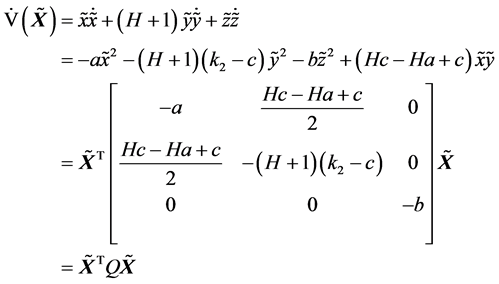
矩阵Q的各阶顺序主子式为
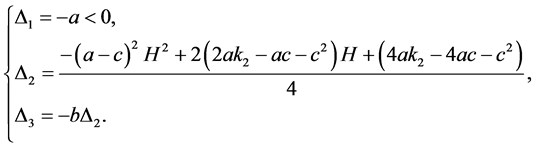
要使矩阵Q是负定的,即 ,只需
,只需
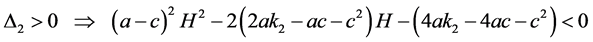 (8)
(8)
当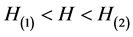 时,式(8)满足。其中,
时,式(8)满足。其中,
 (9)
(9)
由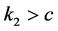 ,应用试探法,可得当
,应用试探法,可得当 时,
时,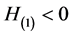 且
且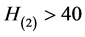 ,则在
,则在 内,式(8)满足,故
内,式(8)满足,故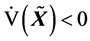 。又因为
。又因为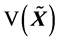 是径向无界的,则被控系统(4)在原点处是全局渐近稳定的。现取
是径向无界的,则被控系统(4)在原点处是全局渐近稳定的。现取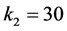 ,则控制器
,则控制器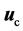 可表示为
可表示为
 (10)
(10)
3.3. 平衡点的唯一性
将式(10)代入式(4),并令式(4)的右边为0,同时令

可得系统(4)关于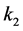 的平衡点分别为原点和
的平衡点分别为原点和
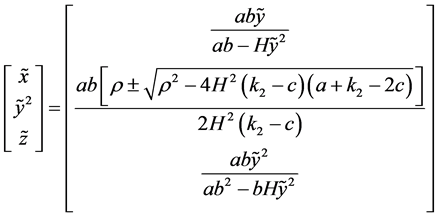
要使原点是被控系统(4)的唯一平衡点,则
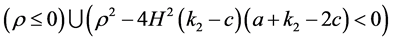 (11)
(11)
求解式(11),可得当
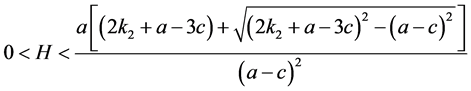 (12)
(12)
时,原点是系统(4)的唯一平衡点。将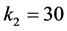 代人式(12),可得
代人式(12),可得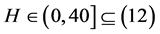 ,即当
,即当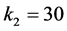 时,在
时,在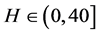 内,原点是被控系统(4)的唯一平衡点。这验证了系统全局渐近稳定的必要条件是在整个状态空间只有一个平衡状态 [16] 。
内,原点是被控系统(4)的唯一平衡点。这验证了系统全局渐近稳定的必要条件是在整个状态空间只有一个平衡状态 [16] 。
3.4. 数值仿真
将式(10)代入式(4),可得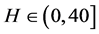 时被控系统(4)的Lyapunov指数谱,如图4中所示。从图4中可以看出,不同H值下系统(4)的Lyapunov指数均为负值,说明系统(4)不再产生周期运动或混沌运动,而是渐近稳定于平衡点原点。因此,线性反馈控制器
时被控系统(4)的Lyapunov指数谱,如图4中所示。从图4中可以看出,不同H值下系统(4)的Lyapunov指数均为负值,说明系统(4)不再产生周期运动或混沌运动,而是渐近稳定于平衡点原点。因此,线性反馈控制器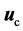 对于H的变化具有一定的鲁棒性,即改变H的取值,仍选择控制器
对于H的变化具有一定的鲁棒性,即改变H的取值,仍选择控制器 如式(10)所示,系统(4)仍可以很好的达到渐近稳定状态 [15] 。
如式(10)所示,系统(4)仍可以很好的达到渐近稳定状态 [15] 。
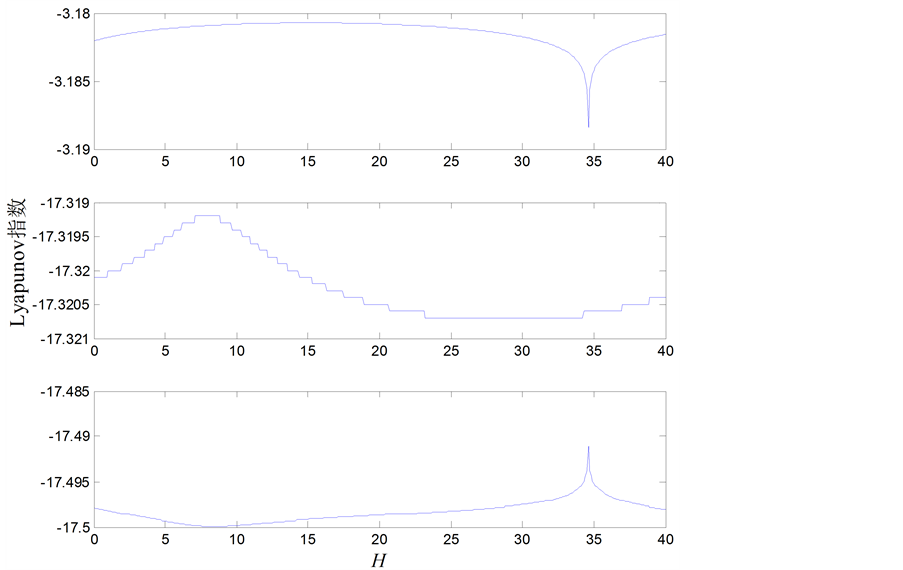
Figure 4. Lyapunov exponent spectrum of the system (4) versus increasing H
图4. 系统(4)随H变化的Lyapunov指数谱
3.5. 应用举例
仍令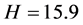 。由上文可知,此时系统处于混沌运动状态。现将式(10)代入式(4)中,可得被控系统(4)的Lyapunov指数分别为
。由上文可知,此时系统处于混沌运动状态。现将式(10)代入式(4)中,可得被控系统(4)的Lyapunov指数分别为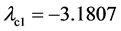 ,
,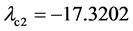 ,
, ,均为负值,被控系统(4)不再产生混沌运动,而是渐近收敛到平衡点原点。
,均为负值,被控系统(4)不再产生混沌运动,而是渐近收敛到平衡点原点。
被控系统(4)的状态曲线如图5中所示。图中横轴t表示式(4)的求解区间,为一无量纲量。从图5中可以看出,状态变量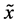 、
、 、
、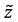 分别渐近收敛于0,且收敛速度很快。说明如式(10)所示的线性反馈控制器
分别渐近收敛于0,且收敛速度很快。说明如式(10)所示的线性反馈控制器 对于控制系统(4)使其不再产生混沌运动而是渐近稳定于零平衡状态是可行的与有效的。
对于控制系统(4)使其不再产生混沌运动而是渐近稳定于零平衡状态是可行的与有效的。
3.6. 控制器的电路实现及控制效果
仍采用改进型模块化电路设计的方法设计控制器电路。对式(10)进行时间尺度变换并设计相应的改进型模块电路,如图2虚线框中所示。该控制电路的状态方程及其电阻的阻值为
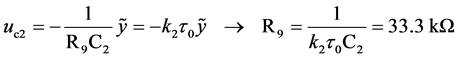
现考察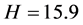 时实际电路的运行结果。调节电阻
时实际电路的运行结果。调节电阻 至
至 ,闭合开关S1,确实可以看到如图3(b1)~(b3)中所示的混沌曲线迅速变为示波器屏幕中心处的一个亮点。说明所设计的线性反馈控制器确实可有效抑制系统的混沌运动,使其渐近稳定于平衡点原点。
,闭合开关S1,确实可以看到如图3(b1)~(b3)中所示的混沌曲线迅速变为示波器屏幕中心处的一个亮点。说明所设计的线性反馈控制器确实可有效抑制系统的混沌运动,使其渐近稳定于平衡点原点。
4. 结论
对于形如N系统的非线性部分包含变化范围已知的可变系数的非线性系统,若直接构造Lyapunov函数求解可使被控系统全局渐近稳定的控制参数,由于控制参数的求解过程中包含可变参数,使得求解
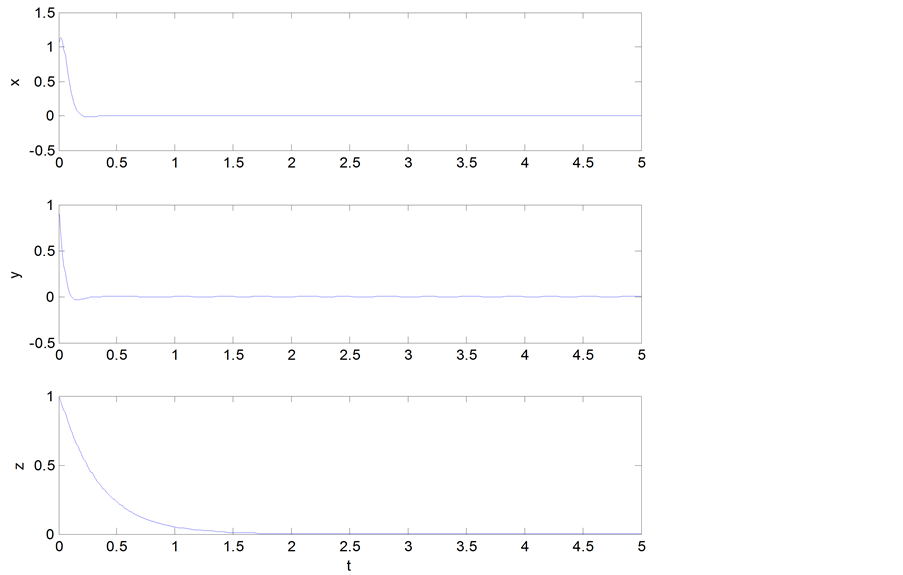
Figure 5. State curves of the system (4)
图5. 系统(4)的状态曲线
过程复杂,不能直观地确定出控制参数的取值范围。而通过对被控系统在原点处进行线性化,消去可变系数对控制参数范围选取的影响,可计算出确定的、使被控系统渐近稳定的控制参数范围。在此基础上构造Lyapunov函数,根据已知控制参数范围,采用试探法确定可使被控系统全局渐近稳定的控制参数范围,有效的简化了控制参数的求解过程,且所得控制器可以是线性的,便于应用于实际电路中。该方法对于非线性部分具有变化范围已知的不确定系数的系统的稳定性控制具有一定的普适性。
由被控系统的建模过程可知,由于对原系统进行了中心平移,本文介绍的改进型Lyapunov方法还可应用于控制系统使其渐近稳定于任意点。同时,若将原系统各状态的中心平移至某一给定状态,该方法还可应用于对给定状态的跟踪中,如混沌或超混沌同步中。关于这一方面的研究将于其他文章中给出具体分析。
文章引用
牛 弘. 具有可变系数的三维混沌系统的稳定性控制与电路实现
Stability Control and Circuit Implementation of a Novel 3D Chaotic System with Variable Coefficient[J]. 动力系统与控制, 2016, 05(01): 31-40. http://dx.doi.org/10.12677/DSC.2016.51004
参考文献 (References)
- 1. Lorenz, E.N. (1963) Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences, 20, 130-141. http://dx.doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
- 2. 陈关荣, 吕金虎. Lorenz系统族的动力学分析、控制与同步[M]. 北京: 科学出版社, 2003.
- 3. 王光义, 丘水生, 许志益. 一个新的三维二次混沌系统及其电路实现[J]. 物理学报, 2006, 55(7): 3295-3301.
- 4. 刘凌, 苏燕辰, 刘崇新. 新三维混沌系统及其电路仿真实验[J]. 物理学报, 2007, 56(4): 1966-1970.
- 5. 王梦蛟, 曾以成, 徐茂林. 一类自治混沌系统的动力学分析与电路实现[J]. 计算物理, 2010, 27(6): 927-932.
- 6. 许喆, 刘崇新, 杨韬. 一种新型混沌系统的分析及电路实现[J]. 物理学报, 2010, 59(1): 131-139.
- 7. 罗明伟, 罗小华, 李华青. 一类四维多翼混沌系统及其电路实现[J]. 物理学报, 2013, 62(2): 161-166.
- 8. 张国山, 牛弘. 一个基于Chen系统的新混沌系统的分析与同步[J]. 物理学报, 2012, 61(11): 137-147.
- 9. Yu, S.M., Lü, J.H. and Chen, G.R. (2007) A Module-Based and Unified Approach to Chaotic Circuit Design and Its Applications. International Journal of Bifurcation and Chaos, 17, 1785-1800. http://dx.doi.org/10.1142/S0218127407018087
- 10. 禹思敏. 混沌系统与混沌电路——原理、设计及其在通信中的应用[M]. 西安: 西安电子科技大学出版社, 2011.
- 11. Ott, E., Grebogi, C. and Yorke, J. (1990) Controlling Chaos. Physical Review Letters, 64, 1196-1199. http://dx.doi.org/10.1103/PhysRevLett.64.1196
- 12. 刘秉正, 彭建华. 非线性动力学[M]. 北京: 高等教育出版社, 2004.
- 13. Jiang, G.P. and Zheng, W.X. (2004) Chaos Control for a Class of Chaotic Systems Using PI-Type State Observer Approach. Chaos, Solitons & Fractals, 21, 93-99. http://dx.doi.org/10.1016/j.chaos.2003.10.001
- 14. Chen, X.R. and Liu, C.X. (2010) Passive Control on a Unified Chaotic System. Nonlinear Analysis: Real World Applications, 11, 683-687. http://dx.doi.org/10.1016/j.nonrwa.2009.01.014
- 15. 牛弘. 混沌及超混沌系统的分析、控制、同步与电路实现[D]: [博士学位论文]. 天津: 天津大学, 2014.
- 16. 刘豹, 唐万生. 现代控制理论. 第3版. 北京: 机械工业出版社, 2006.