Pure Mathematics
Vol.06 No.04(2016), Article ID:18153,7
pages
10.12677/PM.2016.64051
The New Inclusion Region of Eigenvalue Different from 1 for a Stochastic Matrix
Baoxing Zhou1, Huifang Wei2, Yaotang Li1*
1School of Mathematics and Statistics, Yunnan University, Kunming Yunnan
2College of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Jul. 12th, 2016; accepted: Jul. 26th, 2016; published: Jul. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Two new inclusion regions of eigenvalue different from 1 of stochastic matrices are given by using the a-eigenvalue inclusion theorem and the theory of modified matrices; and two new sufficient conditions of stochastic matrices nonsingular are obtained. Numerical examples are given to show that the existing results are improved in some cases.
Keywords:Stochastic Matrices, a1-Matrices, Eigenvalue Different from 1, a-Eigenvalue Inclusion Theorem

随机矩阵非1特征值的新包含区域
周宝星1,卫慧芳2,李耀堂1*
1云南大学,数学与统计学院,云南 昆明
2云南财经大学,统计与数学学院,云南 昆明

收稿日期:2016年7月12日;录用日期:2016年7月26日;发布日期:2016年7月29日

摘 要
利用a-型特征值包含定理及修正矩阵,给出随机矩阵两个新的非1特征值包含区域,并由此得到随机矩阵非奇异的两个新的充分条件。数值例子表明,在某些情况下所得结果改进了几个已有结果。
关键词 :随机矩阵,a1-矩阵,非1特征值,a-型特征值包含定理

1. 引言
随机矩阵是行和为1的非负矩阵,其定义如下:
定义1.1:设非负矩阵 的所有行和等于1,即
的所有行和等于1,即

则称 为(行)随机矩阵。
为(行)随机矩阵。
随机矩阵及其特征值定位在诸如计算机辅助设计、有限Markov过程等领域都有着重要的应用。由非负矩阵的Perron-Frobenius定理 [1] [2] 知,1是任何随机矩阵的主特征值,且 是其对应的一个特征向量。因此对于随机矩阵的特征值定位问题,只需对其所有非1特征值进行定位即可。为了更精确的定位随机矩阵的特征值,LJ. Cvetkovic等在文 [3] 中引入修正矩阵的概念,并将著名的Gersgorin圆盘定理 [4] 应用于修正矩阵,得到如下随机矩阵特征值定位定理。
是其对应的一个特征向量。因此对于随机矩阵的特征值定位问题,只需对其所有非1特征值进行定位即可。为了更精确的定位随机矩阵的特征值,LJ. Cvetkovic等在文 [3] 中引入修正矩阵的概念,并将著名的Gersgorin圆盘定理 [4] 应用于修正矩阵,得到如下随机矩阵特征值定位定理。
定理1.2 [3] [5] :设 为随机矩阵,
为随机矩阵,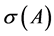 表示
表示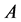 的谱,
的谱, 为
为 的迹。若
的迹。若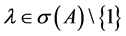 ,则
,则
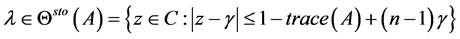
其中 ,
, ,
, 。
。
Shen等在文 [6] 中通过给出随机矩阵非奇异的三个充分条件,得到了随机矩阵非1实特征值的三个包含集。随后,Li等在文 [7] 中推广了Shen的结果,得到如下定理。
定理1.3 [7] :设 为随机矩阵。若
为随机矩阵。若 ,则
,则

其中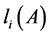 同定理1.2,
同定理1.2, 。
。
定理1.4 [7] :设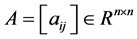 为随机矩阵。若
为随机矩阵。若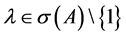 ,则
,则
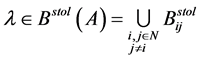
其中 。
。
对于矩阵特征值定位,人们总是力求用尽可能少的计算量得到较为精确的特征值包含区域,但现有的结果还远远没有达到研究者们的期望,因此有必要继续对其进行研究与探索。本文利用a-型特征值包含定理及修正矩阵,研究随机矩阵非1特征值新的包含区域,然后利用其给出随机矩阵非奇异的两个充分条件。
2. 随机矩阵新的非1特征值包含定理
为下文叙述和证明的方便,首先给出一些定义,引理和定理。
定义2.1 [8] :设 ,如果存在
,如果存在 使
使
 ,
,
其中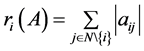 ,则称
,则称 为a1-矩阵。
为a1-矩阵。
定理2.2 [8] :若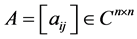 为a1-矩阵,则
为a1-矩阵,则 是非奇异的。
是非奇异的。
定理2.3 [8] :(a-型特征值包含定理):设 ,则
,则

其中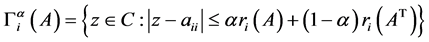 ,
, 。
。
引理2.4 [3] [7] :设 为随机矩阵,
为随机矩阵,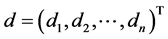 为任一
为任一 维实向量。若
维实向量。若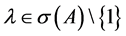 ,则
,则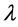 为修正矩阵
为修正矩阵 的特征值。因而若
的特征值。因而若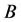 是非奇异的,则
是非奇异的,则 是非奇异的。
是非奇异的。
下面给出随机矩阵非1特征值的两个新的包含定理。
定理2.5:设 为随机矩阵,若
为随机矩阵,若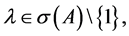 则
则

其中 ,
, ,
,
 ,
,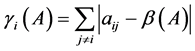 ,
,
证明:令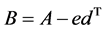 ,其中
,其中 。则有
。则有
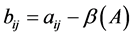 ,
,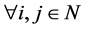 (2.1)
(2.1)
于是
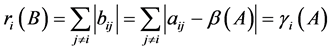 (2.2)
(2.2)
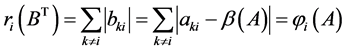 (2.3)
(2.3)
设 ,由引理2.4得
,由引理2.4得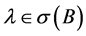 ,由定理2.3知
,由定理2.3知
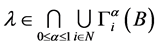
其中 ,
, 。
。
又由(2.1),(2.2),(2.3)得
 ,
,
因此结论成立。
定理2.6:设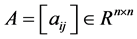 为随机矩阵,若
为随机矩阵,若 ,则
,则
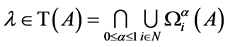
其中 ,
,
 ,
,  ,
, .
.
证明:令 ,其中
,其中 ,则有
,则有
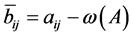 ,
,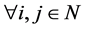 (2.4)
(2.4)
于是
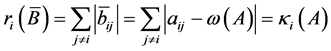 (2.5)
(2.5)
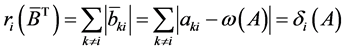 (2.6)
(2.6)
设 ,由引理2. 4得
,由引理2. 4得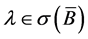 ,再由定理2. 3知
,再由定理2. 3知
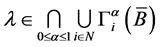
其中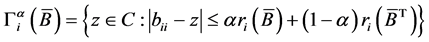 ,
, 。
。
又由(2.4),(2.5),(2.6)得
 ,
,
因此结论成立。
3. 随机矩阵非奇异的两个新充分条件
本节,我们利用第2节所获结果给出随机矩阵非奇异的两个新的充分条件。
定理3.1:设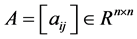 为随机矩阵,若存在
为随机矩阵,若存在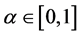 ,使得
,使得
 ,
,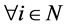 ,
,
则 是非奇异的,其中
是非奇异的,其中 ,
, ,
, 同定理2.5
同定理2.5
证明:(反证法)假设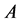 为奇异矩阵,则有
为奇异矩阵,则有 ,由定理2.5得
,由定理2.5得 ,即
,即
对于任意的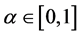 ,存在
,存在 ,使得
,使得

这与条件矛盾,故 是非奇异的。
是非奇异的。
定理3.2:设 为随机矩阵,若存在,使得
为随机矩阵,若存在,使得
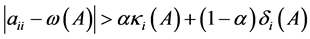 ,
,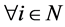
则 是非奇异的,其中
是非奇异的,其中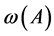 ,
,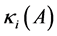 ,
,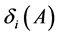 同定理2.6
同定理2.6
证明:(反证法)假设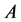 为奇异矩阵,则有
为奇异矩阵,则有 。由定理2.6得
。由定理2.6得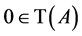 ,即
,即
对于任意的 ,存在
,存在 ,使得
,使得

这与条件矛盾,故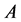 是非奇异的。
是非奇异的。
4. 数值例子
本节我们应用数值例子对本文所获结果与文 [3] 和 [7] 的结果进行比较。下例中统一取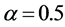 。
。
例4.1:考虑随机矩阵.
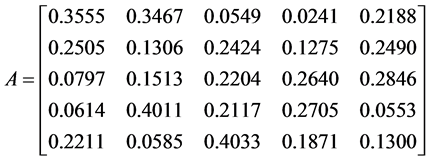 .
.
将定理1.2、定理1.3和定理2.5分别应用于随机矩阵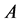 ,经计算得到
,经计算得到 的非1特征值包含集
的非1特征值包含集 ,
, 和
和 ,其关系如图1所示,图中星号表示随机矩阵
,其关系如图1所示,图中星号表示随机矩阵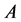 的特征值,蓝色区域表示
的特征值,蓝色区域表示 ,黄色区域表示
,黄色区域表示 ,绿色区域表示
,绿色区域表示 。由图1知,
。由图1知, ,因此
,因此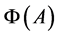 更精确地定位了随机矩阵
更精确地定位了随机矩阵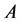 的非1特征值。
的非1特征值。
例4.2:考虑随机矩阵
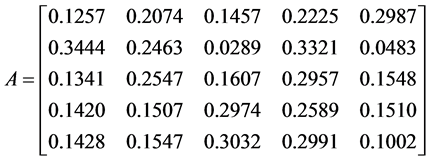 .
.
将定理1.2、定理1.4和定理2.5分别应用于随机矩阵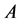 ,经计算得到得到
,经计算得到得到 的非1特征值包含集
的非1特征值包含集 ,
, 和
和 ,其关系如图2所示。图中星号表示随机矩阵
,其关系如图2所示。图中星号表示随机矩阵 的特征值,蓝色区域表示
的特征值,蓝色区域表示 ,黄色区域表示
,黄色区域表示 ,绿色区域表示
,绿色区域表示 。由图2知,
。由图2知,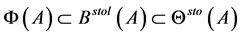 ,因此
,因此 更精确地定位了随机矩阵
更精确地定位了随机矩阵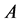 的非1特征值。
的非1特征值。
例4.3:考虑随机矩阵
 .
.
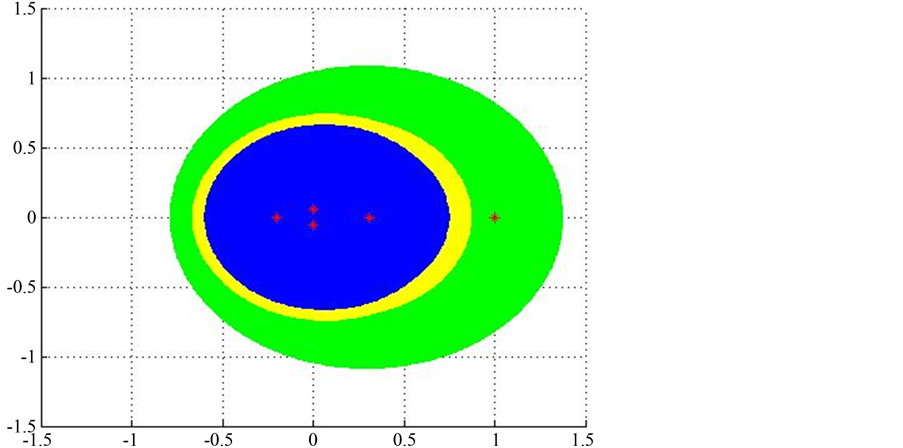
Figure 1. The comparison of Φ(A), Γstol(A), Θsto(A)
图1. Φ(A)、Γstol(A)、Θsto(A)的比较
分别将定理1.3和定理2.5应用于随机矩阵 ,经计算得到
,经计算得到 的非1特征值包含集
的非1特征值包含集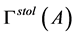 和
和 ,其关系如图3所示。图中星号表示随机矩阵
,其关系如图3所示。图中星号表示随机矩阵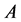 的特征值,蓝色区域表示
的特征值,蓝色区域表示 ,黄色区域表示
,黄色区域表示 。由图3知定理1.3所给区域
。由图3知定理1.3所给区域 和定理2.5所给区域
和定理2.5所给区域 互不包含。
互不包含。
下面我们比较定理2.5和定理2.6。
例4.4:利用MATLAB代码:
K=10; A=rand(k,k); A =inv(diag(sum(A')))*A.
随机产生100个随机矩阵,观察其对应非1特征值包含集的关系见表1。表1显示绝大部分情况下

Figure 2. The comparison of Φ(A), Bstol(A), Θsto(A)
图2. Φ(A)、Bstol(A)、Θsto(A)的比较

Figure 3. The comparison of Γstol(A) and Φ(A)
图3. Γstol(A)和Φ(A)的比较
Table 1. The comparison of Φ(A) and T(A)
表1. Φ(A)和T(A)的比较
Table 2. The comparison of T(A), Γstol(A) and Bstol(A)
表2. T(A)和Γstol(A)、Bstol(A)的比较
定理2.6给出的特征值包含区域比定理2.5给出的特征值包含区域更精确。
例4.5:为了进一步的探讨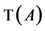 和
和 、
、 的关系,利用MATLAB代码:
的关系,利用MATLAB代码:
K=10; A =rand(k,k); A =inv(diag(sum(A')))*A.
随机产生100个随机矩阵,考察其对应的非1特征值包含集的关系及其个数见表2。表2显示绝大部分情况下定理2.6给出的特征值包含区域比文献 [7] 所给的特征值包含区域更精确。
基金项目
本文受国家自然科学基金资助项目(11361074)资助。
文章引用
周宝星,卫慧芳,李耀堂. 随机矩阵非1特征值的新包含区域
The New Inclusion Region of Eigenvalue Different from 1 for a Stochastic Matrix[J]. 理论数学, 2016, 06(04): 361-367. http://dx.doi.org/10.12677/PM.2016.64051
参考文献 (References)
- 1. Horn, R.A. and Johnson, C.R. (1986) Matrix Analysis. Cambridge University Press, Cambridge, England.
- 2. Seneta, E. (2004) Nonnegative Matrices and Markov Chains. Springer-Verlag, Berlin.
- 3. Cvetković, L., Kostic, V. and Pena, J.M. (2011) Eigenvalue Localization Refinements for Matrices Related to Positivity. SIAM Journal on Matrix Analysis and Applications, 32, 771-784. http://dx.doi.org/10.1137/100807077
- 4. Varga, R.S. (2004) Gersgorin and His Circles. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-17798-9
- 5. Cvetkovic, L., Kostic, V. and Varga, R.S. (2004) A New Gersgorin-Type Eigenvalue Inclusion Set. Electronic Transactions on Numerical Analysis, 18, 73-80.
- 6. Shen, S.Q., Yu, J. and Huang, T.Z. (2014) Some Classes of Nonsingular Matrices with Applications to Localize the Real Eigenvalues of Real Matrices. Linear Algebra and Its Applications, 447, 74-87. http://dx.doi.org/10.1016/j.laa.2013.02.005
- 7. Li, C.Q., Liu, Q.B. and Li, Y.T. (2014) Gersgorin-Type and Brauer-Type Eigenvalue Localization Sets of Stochastic Matrices. Linear and Multilinear Algebra.
- 8. Cvetković, L. (2007) H-Matrix Theory vs. Eigenvalue Localization. Numerical Algorithms, 42, 229-245.
